Single Channel Source Separation Using Filterbank and 2D Sparse Matrix Factorization ()
1. Introduction
Blind source separation has gained a great deal of attention in signal processing applications and these consist of medical signal analysis, telecommunications and speech recognition. There is an essential topic known as single channel source separation (SCSS) [1,2] which has not yet been enhanced enough to make its way out of laboratories. In recent years, new advances have been achieved in SCSS and this can be categorized into two main branches: supervised SCSS methods (e.g. model-based SCSS [3-6] techniques) and unsupervised SCSS methods (e.g. nonnegative matrix factorization (NMF) [7] and computational auditory scene analysis (CASA) [8]). In this paper, we proposed a novel unsupervised SCSS method based on non-negative matrix factorization approach.
NMF methods have been widely exploited in the field of SCSS, and especially being used in separating audio mixtures, e.g. extracting drums from polyphonic music [9] and automatic transcription of polyphonic music [10]. Families of parameterized NMF cost functions such as the Beta divergence [11] and Csiszar’s divergences [12] have been presented for the separation of audio signals [13] and in general case, the least square distance [14]
and the Kullback-Leibler (KL) divergence [15] are two main cost functions which have been widely employed in NMF. However, the problem where conventional NMF methods fail in SCSS is when two notes are played simultaneously in which case they will be modeled as one component [7]. To overcome this limitation, the sparse non-negative matrix two dimensional deconvolution (SNMF2D) [16] is derived to track the spectral frequencies of the sources that change over time.
This paper presents a novel method based on SNMF2D and filterbank technique. The audio mixture is generated by sources composed of two different origins audio signals but received synchronously by one microphone. Intuitively, the proposed separation strategy utilizes filterbank to make the observed mixed signal analyzed in sub-band domain. The impetus behind this is that the degree of mixing of the sources in the sub-band domain is now less ambiguous and thus, the dominating source in the sub-band mixture can be easily detected. Therefore, the spectral and temporal patterns (i.e. the spectral bases and temporal codes, respectively) associated in each sub-band can be extracted more accurately by using SNMF2D. Once the sub-sources are obtained the kmeans based clustering method is used to group these sub-sources into clusters where each cluster consist a set of sub-sources [17,18] which will be subsequently used for recovering the original sources. The proposed method concentrates on the idea of performance source separation in the sub-band domain and avoids directly estimateing the sources using the mixture signal which contains too many mixing ambiguities between sources. In this way, we show that the proposed method can make a superior separation performance.
The paper is organized as follows: In Section 2, the proposed source separation framework is fully developed. In Section 3, experimental results are presented. The impact factors and a series of performance comparison are discussed in Section 4. Finally, Section 5 concludes the paper.
2. Proposed Model
The single channel audio mixture 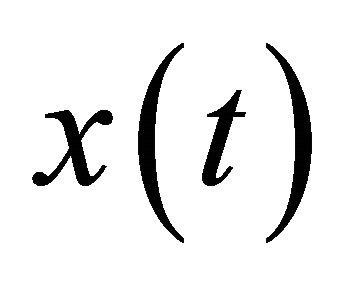 is given as:
is given as:
 (1)
(1)
where  denotes time index. The goal of SCSS is to estimate the two sources
denotes time index. The goal of SCSS is to estimate the two sources  and
and 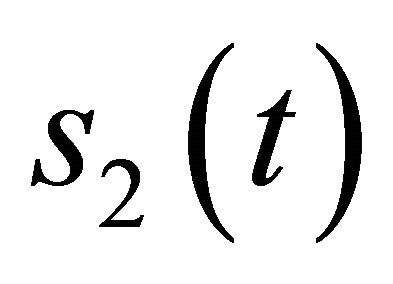 when only the observation signal
when only the observation signal  is available.
is available.
The core procedure of the proposed method is shown in Figure 1. It consists of two main techniques-filterbank and SNMF2D. The benefits filterbank bring to SCSS are 1) the degree of mixing ambiguity from the original sources is reduced in that particular sub-band signal; and 2) the complexity of the spectral and temporal patterns associated with each sub-band will be simpler and sparser as compared with that of the mixed signal. The specific steps of the proposed method are summarized as follows:
Step 1: Transform the mixture from time domain into sub-band domain using filterbank, and then down-sampling the signal for reducing the aliasing problem. Hence, instead of processing the mixed signal directly, the subband signals are utilized as the new set of observations.
Step 2: Convert the sub-band mixed signals into timefrequency (TF) domain by using STFT (Short-Time Fourier Transform) and then construct log-frequency magnitude spectrogram, utilize SNMF2D to decompose the sub-band mixing TF mixtures into source related spectral and temporal patterns. The separated time domain subsources can be reconstructed by using the inverse STFT.
Step 3: Use the k-means clustering method to group the sub-sources into different clusters where each cluster consist a set of sub-sources correspond to one recovered source.
Step 4: Recover the time domain sources in the synthesis stage.
1) Pre-processing stage: Filterbank includes low-pass, band-pass, and high-pass filters which are served to isolate different frequency components in a signal. The perfect filterbank will be designed so that the output source is the same as the input source with no distortion through a time shift and amplitude scaling. Here, the down-sampling is served to reduce the aliasing [19-21] problem. In the sub-band analysis, the formulation of filterbank is given as follow:
 (2)
(2)
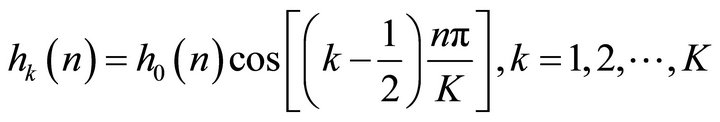 (3)
(3)
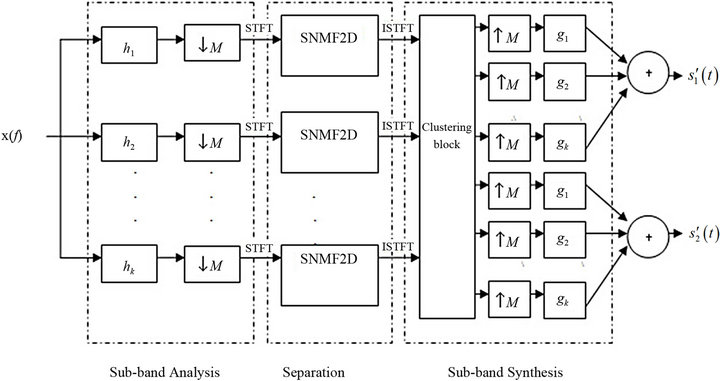
Figure 1. Core procedure of the proposed method.
where the finite number of sub-bands is ,
,  is the length of window, the cut-off frequency is defined as
is the length of window, the cut-off frequency is defined as
 and
and 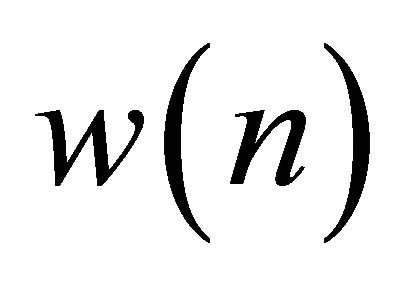 is the Hamming window given by
is the Hamming window given by
 (4)
(4)
In this paper, the observations after filterbank processing can be effectively down-sampled by an integer decimation factor  (down-sampling rate) in each sub-band. The down-sampled observation
(down-sampling rate) in each sub-band. The down-sampled observation  in the kth
in the kth 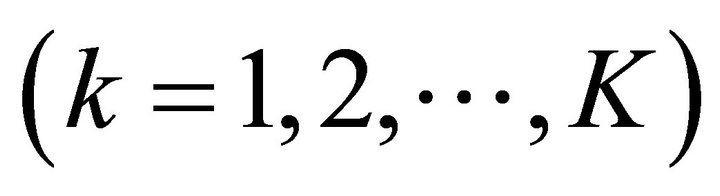 sub-band is generated by using Equation (5), where
sub-band is generated by using Equation (5), where  denotes the time index at the reduced sampling rate for some integer
denotes the time index at the reduced sampling rate for some integer , and
, and 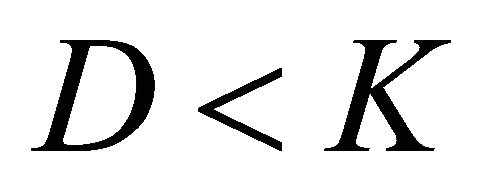 for avoiding [21] any aliasing distortion.
for avoiding [21] any aliasing distortion.
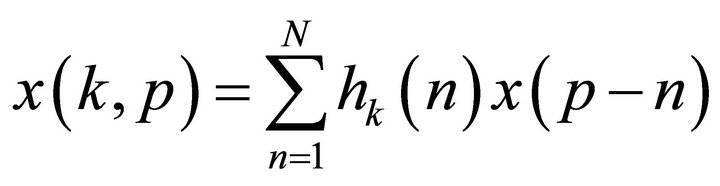 (5)
(5)
2) Separation stage: Once the new set of observations 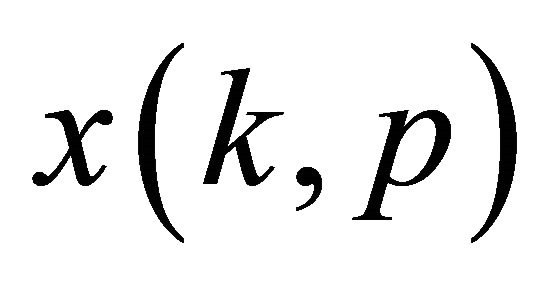 has been generated, the sub-band mixed signals are transformed to the time-frequency (TF) domain using STFT. We then group the spectrogram bins into 175 logarithmically spaced frequency bins in the range of 50 Hz to 8 kHz with 24 bins per octave, which corresponds to twice the resolution of the equal tempered musical scale to construct log-frequency [7] magnitude spectrogram. Within the context of SCSS, the TF representation of the mixture in (1) is given by
has been generated, the sub-band mixed signals are transformed to the time-frequency (TF) domain using STFT. We then group the spectrogram bins into 175 logarithmically spaced frequency bins in the range of 50 Hz to 8 kHz with 24 bins per octave, which corresponds to twice the resolution of the equal tempered musical scale to construct log-frequency [7] magnitude spectrogram. Within the context of SCSS, the TF representation of the mixture in (1) is given by
 (6)
(6)
where  and
and
 are two-dimensional matrices
are two-dimensional matrices
(row and column vector represents the time slots and frequencies, respectively). In this paper, we term the sources at each sub-band as the sub-sources. To estimate these sub-sources, we project all the sub-band mixed signals from (5) into the TF domain, in which can be denoted as:
 (7)
(7)
 and
and 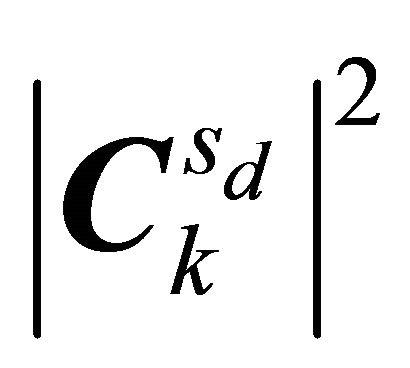 denotes TF representations of the kth sub-band mixture
denotes TF representations of the kth sub-band mixture  and dth source, respectively. The matrices we are interested to determine are
and dth source, respectively. The matrices we are interested to determine are
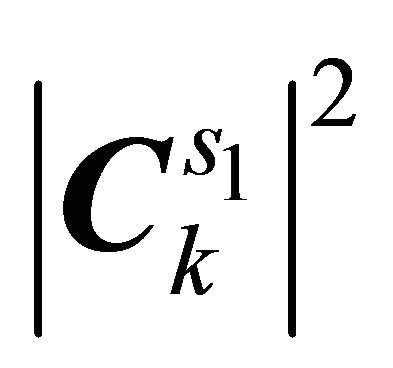 and
and  which can be estimated using any non-negative matrix factorization algorithm. In our approach, we favours the SNMF2D algorithm where the desirable matrices can be estimated as
which can be estimated using any non-negative matrix factorization algorithm. In our approach, we favours the SNMF2D algorithm where the desirable matrices can be estimated as
 and
and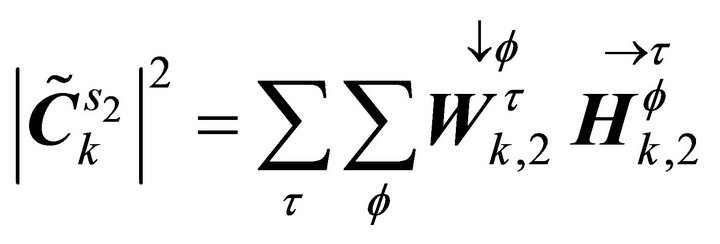 .
.
Here, 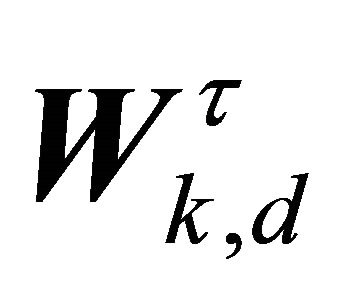 denotes the dth column of
denotes the dth column of 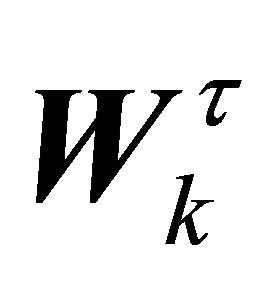 that corresponds to the dth row of
that corresponds to the dth row of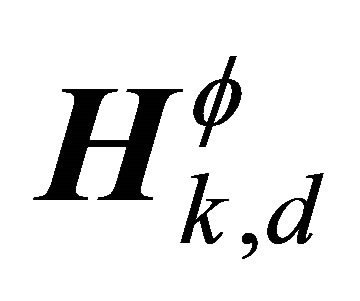 . In the case of two sources, we have
. In the case of two sources, we have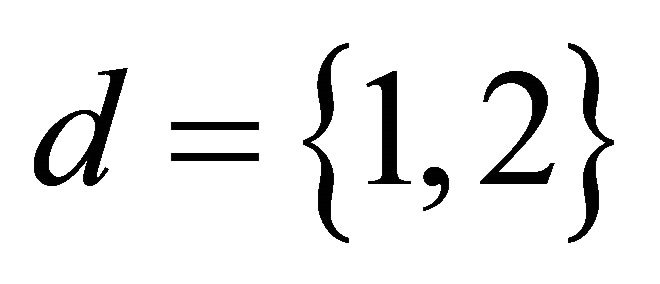 . The reasons SNMF2D [19,20] are favoured over other conventional NMF methods are noted as follows: 1) The NMF does not model notes but rather unique events only. Thus, if two notes are always played simultaneously they will be modelled as one component; 2) The structure of a factor in H can be input into signature of the same factor in W and vice versa. Thus, this leads to ambiguity that can be resolved by forcing the structure on W through imposing sparseness on H. The two basic cost functions for optimizing
. The reasons SNMF2D [19,20] are favoured over other conventional NMF methods are noted as follows: 1) The NMF does not model notes but rather unique events only. Thus, if two notes are always played simultaneously they will be modelled as one component; 2) The structure of a factor in H can be input into signature of the same factor in W and vice versa. Thus, this leads to ambiguity that can be resolved by forcing the structure on W through imposing sparseness on H. The two basic cost functions for optimizing  and
and  are given by the Least Squares (LS) distance and Kullback-Leibler divergence (KLd) where
are given by the Least Squares (LS) distance and Kullback-Leibler divergence (KLd) where is a sparseness parameter and
is a sparseness parameter and :
:
LS: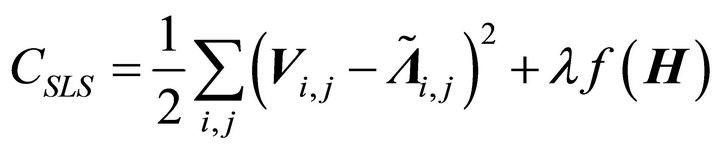 (8)
(8)
KLd: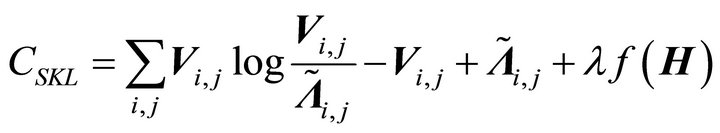 (9)
(9)
In above, 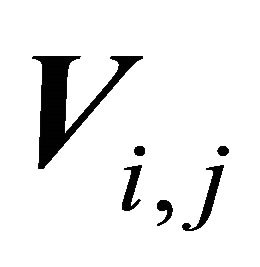 is the log-frequency magnitude spectrogram,
is the log-frequency magnitude spectrogram,  is the data matrix of the sub-band TF mixture and
is the data matrix of the sub-band TF mixture and 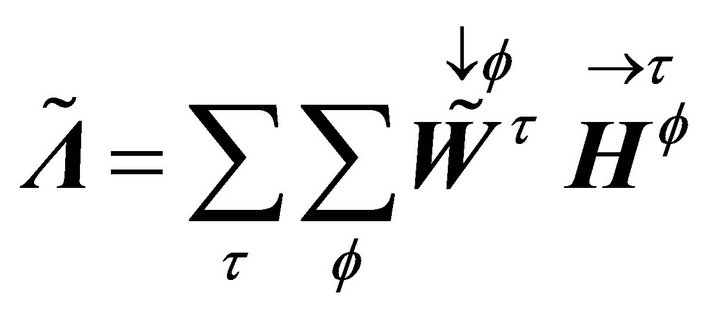 where
where
 . The derivatives of (8) with respect to
. The derivatives of (8) with respect to 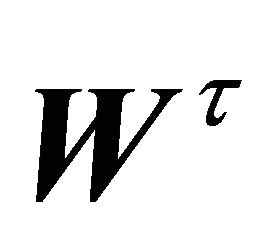 and
and  are given by:
are given by:
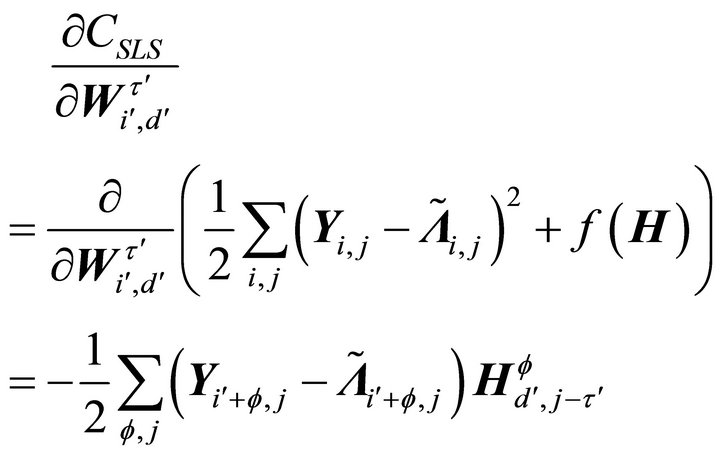 (10)
(10)
 (11)
(11)
Thus, by applying the standard gradient decent approach, we have:
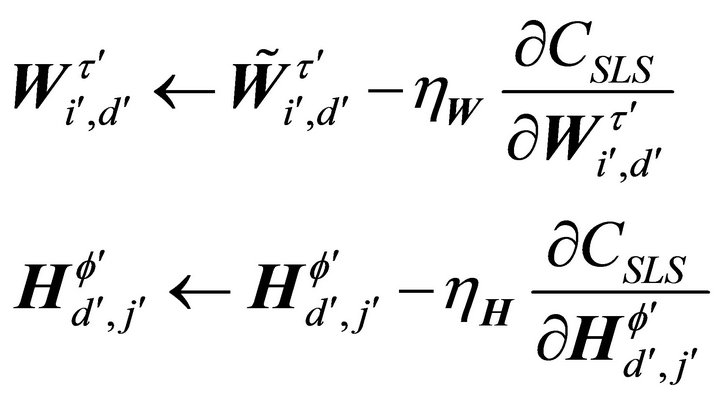 (12)
(12)
where  and
and  are positive learning rates which can be obtained by following the approach of Lee and Seung [15], namely,
are positive learning rates which can be obtained by following the approach of Lee and Seung [15], namely,  and
and
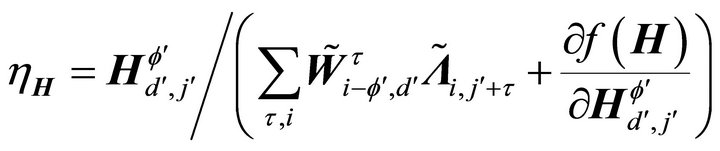 . Thus, in matrix notation, by using the multiplicative learning rules, the SNMF2D algorithm are summarized in Table 1. In these tables, the superscript “
. Thus, in matrix notation, by using the multiplicative learning rules, the SNMF2D algorithm are summarized in Table 1. In these tables, the superscript “ ” denotes vector transpose, “
” denotes vector transpose, “ ” is the element-wise product and at each iteration,
” is the element-wise product and at each iteration, 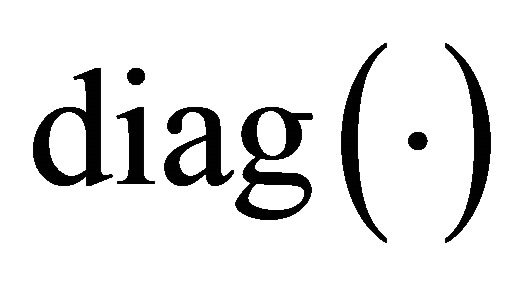 denotes a matrix with the argument on the diagonal. The column vectors of
denotes a matrix with the argument on the diagonal. The column vectors of  will be factor-wise normalized to unit length.
will be factor-wise normalized to unit length.
After using mask, the sub-sources 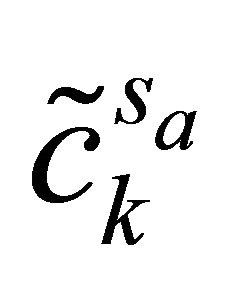 can be obtained:
can be obtained:
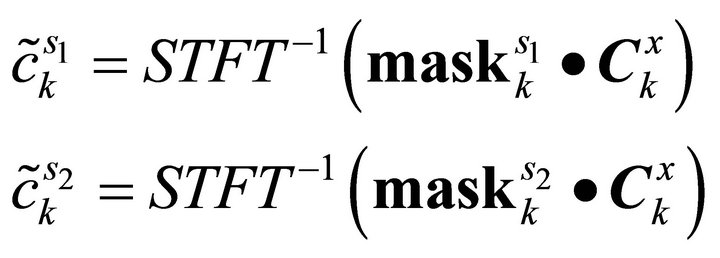 (13)
(13)
where the masks are determined element-wise by:
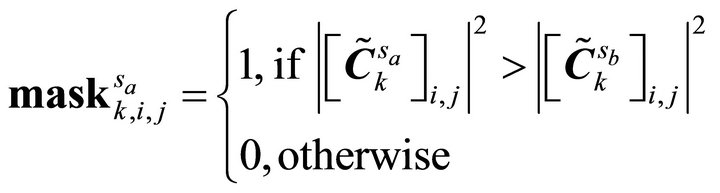 (14)
(14)
3) Clustering stage: Once the sub-sources are obtained by using inverse STFT, the k-means based clustering method is used to group these sub-sources into clusters according to the number of sources. In this case, the k-means method aims to separate 2 K observations (K is number of sub-bands) into two clusters (corresponding to two sources). After convergence, all sub-sources will be grouped into their respective clusters which are given denoted as 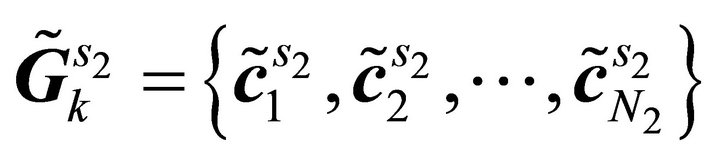 and
and
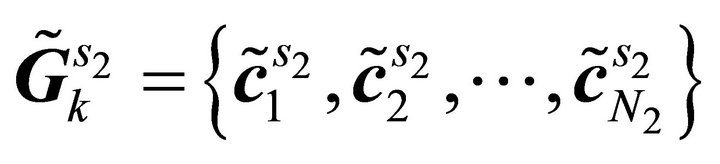 which contains
which contains 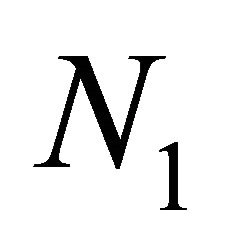 and
and 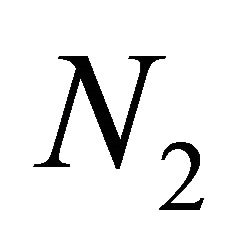
number of sub-sources that belong to Source 1 and Source 2, respectively.
4) Synthesis stage: After up-sampling, the filterbank synthesis process is used to recombine all the subsources to form the estimated source signals. A series of expansions of the output can be reconstructed by using the time-shifted variants 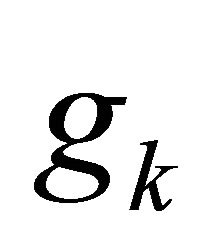 (synthesis filter) [19-21]. The process is expressed as follow:
(synthesis filter) [19-21]. The process is expressed as follow:
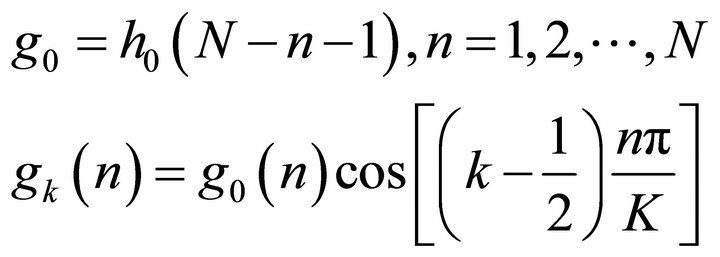 (15)
(15)
Finally, the recovered sources from each cluster can be estimated as
 (16)
(16)
where  denotes the time index at the restored sampling rate
denotes the time index at the restored sampling rate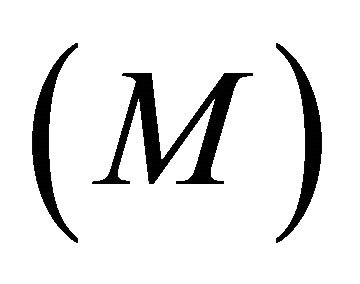 .
.
3. Experimental Results
The proposed monaural source separation algorithm is tested on recorded audio signals. Several experimental studies have been designed to investigate the efficacy of the proposed approach. All simulations and analysis are conducted using a PC with Intel Core 2 CPU 6600 @ 2.4 GHz and 2 GB RAM. For mixture generation, two sentences of the target speakers (male and female) “fcjf0” and “mcpm0”, were selected from TIMIT speech data-
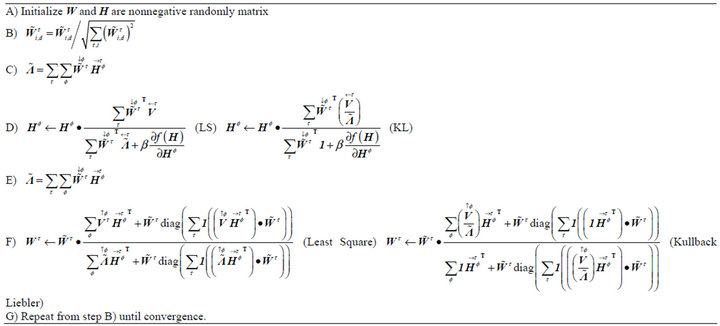
Table 1. SNMF2D (LS and KL) algorithm.
base and the others including flute, bass and drum music. All mixtures are sampled at 16 kHz sampling rate and the length of all test signals was chosen to be (40,000 samples, approximately 2.5 s). The time-frequency representation was computed by normalizing the time-domain signals to unit power and we computed the STFT using 1024 point Hanning window FFT with 50% overlap. The spectrogram bins are grouped into 175 logarithmically spaced frequency bins in the range of 50 Hz to 8 kHz with 24 bins per octave, which corresponds to twice the resolution of the equal tempered musical scale. As for the filterbank, the parameter corresponding to the total number of filters  is set as 4 and the length of the hamming window is defined equal to 128. As for SNMF2D parameters, the convolutive components in frequency and time were selected as
is set as 4 and the length of the hamming window is defined equal to 128. As for SNMF2D parameters, the convolutive components in frequency and time were selected as 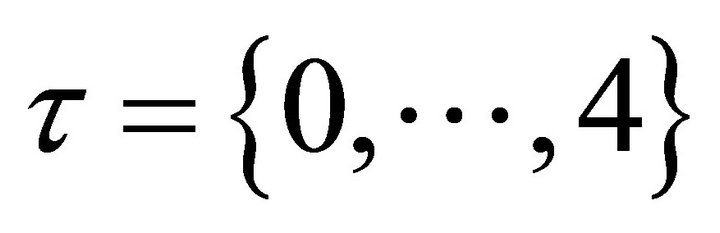 and
and , respectively. The sparse regularization term is set to
, respectively. The sparse regularization term is set to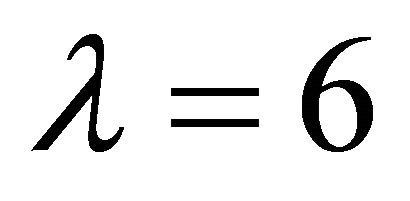 . Figure 2 shows the design of four sub-bands.
. Figure 2 shows the design of four sub-bands.
Using the filterbank is very useful and helpful for the separation stage. This is because one of original sources may centralize its basic frequency information in a specific sub-band such that the dominant source can be easier extracted using source separation algorithms such as the SNMF2D. In the separation stage, the observed signal in each sub-band is converted into the log-frequency spectrogram and decomposed by SNMF2D. The cost value of decomposing female speech mixed with bass music in each sub-band is shown in Figure 3. It is observed that the decomposition process converges to a low steady value after approximately 40 iterations for all sub-band mixtures by using the SNMF2D algorithm. Figure 4 shows an example of H and W as decomposed in the fourth sub-band mixed signal. It is seen that the spectral bases and temporal codes of each source are distinguishable so that each spectral basis can represent the frequency patterns of one sub-sources. The example of final separation results are shown in Figure 5.
The measure distortion between the original source

Figure 3. Convergence of LS cost function.
 (a)
(a)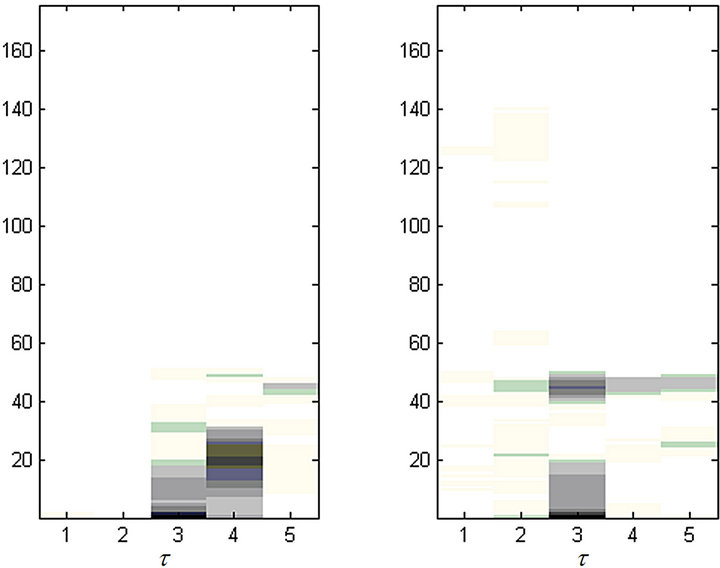 (b)
(b)
Figure 4. (a) H (in fourth sub-band); (b) W (in fourth sub-band).

Figure 5. Original signals (blue) and recovered signals (red) using proposed method.
and the estimated one is computed by using the improvement of signal-to-noise ratio (ISNR) [22] defined as:
 (17)
(17)
The ISNR is used as the quantitative measure of separation performance and the average ISNR will be tabulated in the evaluation tables. The ISNR represents the degree of suppression of the interfering signals to improve the quality of the target signal. It has been commonly used to measure the separation quality between the mixed and separated signal. The higher value of ISNR indicates better separation performance. In this paper, six types of mixture have been generated: 1) flute mixed with male speech; 2) flute mixed with female speech; 3) bass mixed male speech; 4) bass mixed female speech; 5) drum mixed male speech and 6) drum mixed female speech. All separation results have been summarized in Figure 6 where 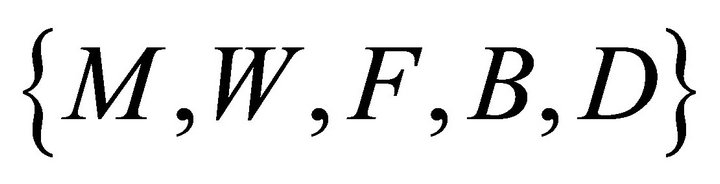 represent male speech, female speech, flute music, bass music and drum music. The separation of speech-bass music mixture is much better than those of other types of mixtures where the average ISNR has approached to 10 dB for recovered speech signal and 4 dB for recovered bass music.
represent male speech, female speech, flute music, bass music and drum music. The separation of speech-bass music mixture is much better than those of other types of mixtures where the average ISNR has approached to 10 dB for recovered speech signal and 4 dB for recovered bass music.
Figure 6 summarizes the separation results of our proposed method. It is worth pointing out that because the frequency range of bass and drum music locate at very lower frequency region, the lower frequency bands are dominated with most energy from the bass or drum components through filterbank process. Hence, it is easier to extract these lower frequency components by using the SNMF2D. Thus, Figure 6 shows the relatively better separation results when audio mixture contains bass or drum music. On the other hand, the frequency range of flute is very similar to speech sources (as indicated in Figure 9) and this particular mixture is very difficult to separate which explains the reason why the ISNR is relatively low. However, this performance is still substantially better than using the SNMF2D alone.
4. Discussion
4.1. Effects on Audio Mixtures Separation with/without Filterbank Preprocessing
The benefits filterbank preprocessing bring to SCSS is that since a filtered signal bounded within a particular range of sub-band frequencies, the complexity of the spectral and temporal patterns associated with each subband signal will be simpler and sparser than that of the mixed signal. This effectively means that there is a relatively clear distinction of the spectral and temporal patterns between the dominating source and the less dominating one in the TF domain in each sub-band. This is shown in Figures 7 and 8.
Figures 9 and 10 further show the time domain subband signal. It is clearly visible that the mixing at the different sub-band is dominated either by Source 1 or Source 2. In this example, it can be seen that flute music dominates the 1st sub-band while male speech dominates the 2nd-4thsub-band. The final comparison results of audio mixtures separation with/without filter-bank preprocessing are given in Figure 11.
4.2. Impact of Sparsity Regularization
In the separation stage, λ (sparse regularization), an essential parameter influences separation results. In Figure 7, we use an example-mixture of male speech and flute music for analyzing the impact of sparsity regularization. The separation results are concluded given different levels of sparse λ based on either LS or KLd cost functions. It is observed that the best ISNR has been found with the sparse factor λ = 6 by using the LS cost function and λ = 20 by using the KLd cost function. In addition, the LS cost function based decomposition reflects the local minimum whereas the KLd based decomposition returns the global minimum. However, our results have shown that both LS and KLd methods give comparable performance as shown in Table 2.
In this section, we develop a test to compare the separation performance between the proposed method and SNMF2D SCSS method. Figure 11 shows that the ISNR results obtained using the proposed method which renders considerable improvements over the SNMF2D SCSS method. An average improvement of 1.8 dB per source is obtained across all the different type of mixtures for proposed method when compared to SNMF2D SCSS method. The specific comparison results are summarized as follows: 1) for mixture of speech and flute music, the average improvement is about 3.4 dB; 2) for mixture of speech and bass music, the improvement is 1.5 dB; 3) for mixture of speech and drum music, the average improvement is approximately 0.2 dB.
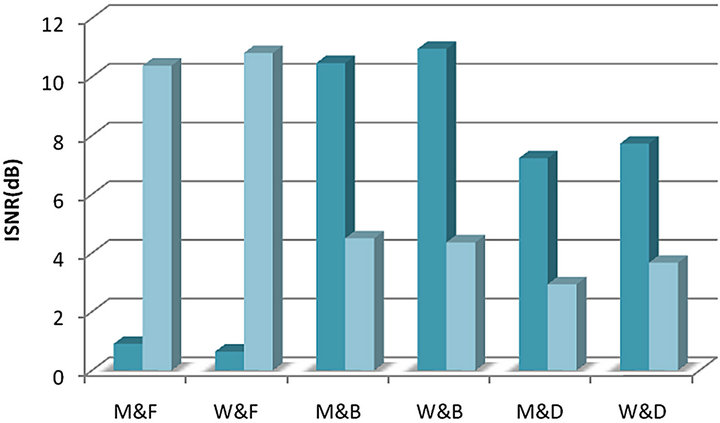
Figure 6. Separation results using the proposed method.
 (a)
(a)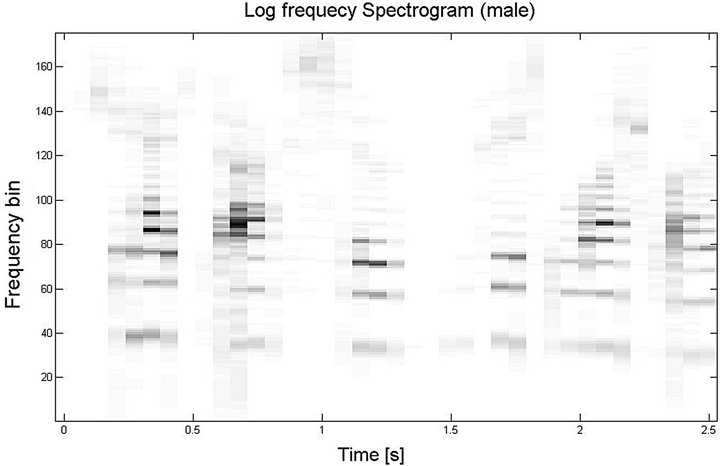 (b)
(b) (c)
(c)
Figure 7. (a) and (b) denote the log-frequency spectrogram of flute music and male speech, respectively; (c) denotes the logfrequency spectrogram of mixed signal (flute + male).
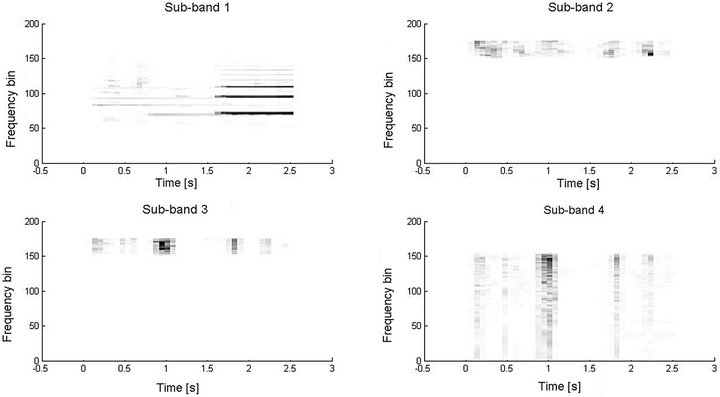
Figure 8. Log-frequency mixed spectrogram with filter-bank processing.
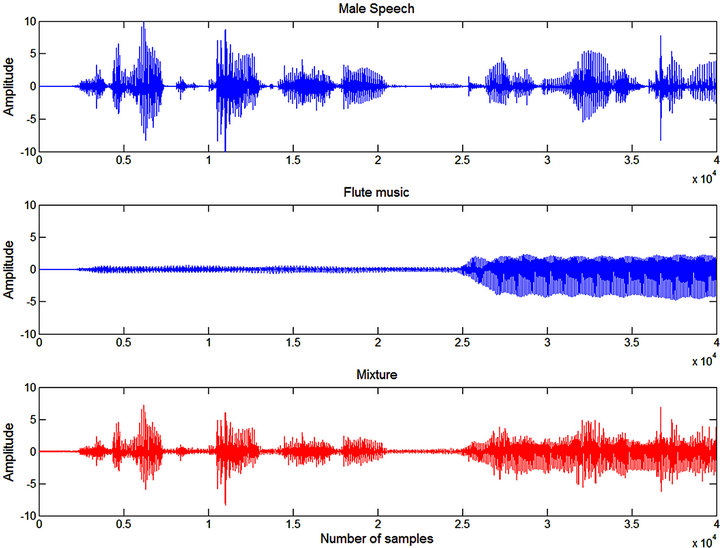
Figure 9. Time domain signals (flute music and male speech).

Figure 10. Time domain sub-band signals with filter-bank processing.
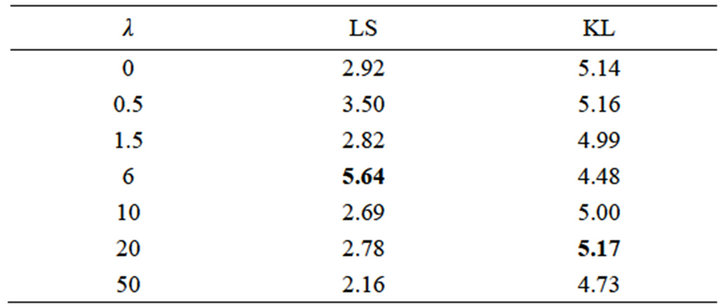
Table 2. Separation results by using different sparse regularization.
5. Conclusion
This paper has presented a novel framework of amalgammating filterbank technique with two-dimensional sparse non-negative matrix deconvolution (SNMF2D) for single channel source separation. Although proposed method and the SNMF2D SCSS method can extract sources from single channel mixture, the results obtained from our approach outperform that of using the SNMF2D. The strength of the proposed method: 1) it does not rely on training information so that it is more practical; 2) the degree of mixing ambiguity in each sub-band is less ambiguous than those in mixed signal; therefore the subband mixtures are simpler and sparser, and hence the spectral and temporal patterns can be efficiently extracted. Considerable improvements have been achieved in terms of ISNR by using our proposed method.