1. Introduction
The study of scalar truncated moment problems is the subject of many remarkable papers such as: [1-3]. In [2], the problem of finding scalar atomic representing measure for the terms of a finite scalar sequence of complex numbers as multidimensional moment terms is studied.
In [2], with the Hankel matrix 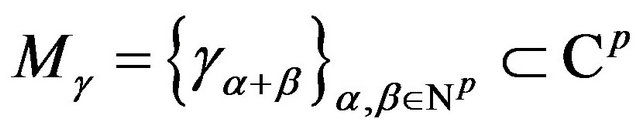
with rank r, the necessary and sufficient existence condition of an atomic representing measure with exactly r atoms for the sequence 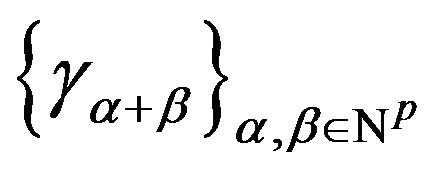 is the existence of a “flat extension”. A “flat extension” is a rank preserving, nonnegative extension
is the existence of a “flat extension”. A “flat extension” is a rank preserving, nonnegative extension  of
of , associated with a larger moment sequence
, associated with a larger moment sequence  A main result in [2], establishes some algebraic relations between the condition in which the support of the representing measure of the given sequence
A main result in [2], establishes some algebraic relations between the condition in which the support of the representing measure of the given sequence 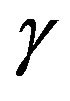 is contained in the algebraic variety of zerous of a suitable polynomial and the dependence relations established between the columns of the Hankel matrix
is contained in the algebraic variety of zerous of a suitable polynomial and the dependence relations established between the columns of the Hankel matrix . These relations are expressed, also, as zerous of the mentioned polynomial. In [1], the concept of “flat extension” of the Hankel matrix of truncated scalar multidimensional moment sequence is substituted with the concept of “dimension stability” of the algebraic dimension of the Hilbert space obtained as the separation of the space of scalar polynomials with total degree m, with respect to the null subspace of a unital, square positive functional, the Riesz functional. The Riesz functional is in bijection with a moment functional, positive on the cone of sums of squares of real polynomials. The stability condition of the algebraic dimension of such Hilbert space affords in [1] an algebraic condition for obtaining some commutative tuple of selfadjoint operators, defined on the Hilbert space of stable dimension. In the same time, in [1], by extending the Riesz functional on the whole space of polynomials, using the functional calculus of the constructed commutative selfadjoint tuple, the arbitrary powers of it are organized as a
. These relations are expressed, also, as zerous of the mentioned polynomial. In [1], the concept of “flat extension” of the Hankel matrix of truncated scalar multidimensional moment sequence is substituted with the concept of “dimension stability” of the algebraic dimension of the Hilbert space obtained as the separation of the space of scalar polynomials with total degree m, with respect to the null subspace of a unital, square positive functional, the Riesz functional. The Riesz functional is in bijection with a moment functional, positive on the cone of sums of squares of real polynomials. The stability condition of the algebraic dimension of such Hilbert space affords in [1] an algebraic condition for obtaining some commutative tuple of selfadjoint operators, defined on the Hilbert space of stable dimension. In the same time, in [1], by extending the Riesz functional on the whole space of polynomials, using the functional calculus of the constructed commutative selfadjoint tuple, the arbitrary powers of it are organized as a 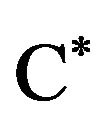 algebra of the same stable dimension. The problem of stability of the algebraic dimension of some Hilbert space obtained in this way is naturally connected, via the existence of a commuting tuple of self adjoint operators, with that of solving a scalar truncated multidimensional moment problem. The representing measure of the finite dimensional moment sequence is, in [1], the spectral atomic joint measure associated with the constructed commutative selfadjoint tuple, and has the same number of atoms as the stable algebraic dimension. Truncated operatorvalued problems is the subject in papers [4-7], to quote only a few of them. In [7] a Hausdorff truncated unidimensional operator-valued moment problem is studied. For obtaining the representing measure the Kolmogorov’s decomposition theorem is used. The given positive kernel of operators in [7] acts on an arbitrary, separable Hilbert space, all operators are linear independent, also the number of operators is arbitrary, even or odd.
algebra of the same stable dimension. The problem of stability of the algebraic dimension of some Hilbert space obtained in this way is naturally connected, via the existence of a commuting tuple of self adjoint operators, with that of solving a scalar truncated multidimensional moment problem. The representing measure of the finite dimensional moment sequence is, in [1], the spectral atomic joint measure associated with the constructed commutative selfadjoint tuple, and has the same number of atoms as the stable algebraic dimension. Truncated operatorvalued problems is the subject in papers [4-7], to quote only a few of them. In [7] a Hausdorff truncated unidimensional operator-valued moment problem is studied. For obtaining the representing measure the Kolmogorov’s decomposition theorem is used. The given positive kernel of operators in [7] acts on an arbitrary, separable Hilbert space, all operators are linear independent, also the number of operators is arbitrary, even or odd.
In the present note, the stability dimension concept in [1], in the following way is adapted: a positive finite operator-valued kernel acting on a finite dimensional Hilbert space is given; a hermitian square positive functional on the space of vectorial functions, via the given kernel, is introduced. The restrictions of the hermitian square positive functional to some subspaces of the vectorial functions are considered. The separation spaces with respect to the null subspaces of these hermitian square positive restricted functionals are obtained. The stability dimensional condition for the obtained Hilbert spaces, in the same way as in [1], affords a construction of a commuting tuple of selfadjoint oparators, defined on the Hilbert space of the stable dimension. The obtained commuting tuple of selfadjoint operators, produced an integral representing joint spectral measure of all powers of the tuple. Via Kolmogorov’s theorem of decomposition of positive operator kernels, a representing positive operator-valued measure as Hausdorff truncated multidimensional moment sequence for all terms in the given kernel is obtained. The first terms of the given kernel, in number equal with “d”—the stable dimension, are linear independent, are integral represented with respect to an atomic operator valued measure with exactely “d” atoms, the remainder terms in the kernel are integral represented with respect to the same measure and the same number of atoms as the first one. The possibility of extension of the given operator sequence with preserving the “stability condition”, as well as the number of atoms of the representing measure is also analysed. In the present note, the number of operators in the given kernel is only even.
In this note, in Section 3 to a positive-definite kernel of operators a square positive functional is attached. The Hilbert spaces obtained as the quotient of some finite dimensional spaces and subspaces of vectorial functions with respect to the null spaces associated with the square positive functional and its restrictions are constructed. The problem of stability of the dimension of the Hilbert spaces in Section 3 and its implications in solving multidimensional, truncated Hausdorff operator-valued moment problems in Section 4, in this note is analysed.
2. Preliminaries
When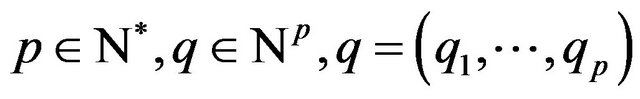 and
and  the p-dimensional real variable, are arbitrary, we denote with
the p-dimensional real variable, are arbitrary, we denote with ; the addition and substraction in
; the addition and substraction in 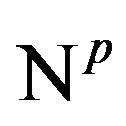 are considered on components. For H an arbitrary Hilbert space,
are considered on components. For H an arbitrary Hilbert space, 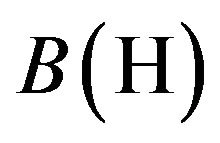 represents the algebra of linear, bounded operators on H, for
represents the algebra of linear, bounded operators on H, for  a commuting tuple of multioperators,
a commuting tuple of multioperators,  for all
for all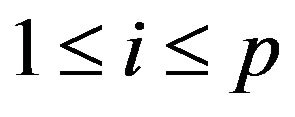 , we denote with
, we denote with  . For an arbitraty
. For an arbitraty 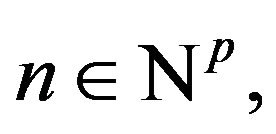 the function
the function , is:
, is:
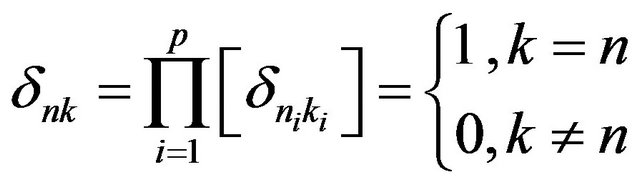
with 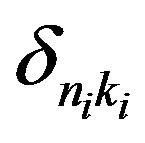 the Kronecker symbol. For
the Kronecker symbol. For  we consider the spaces of vectorial functions:
we consider the spaces of vectorial functions:
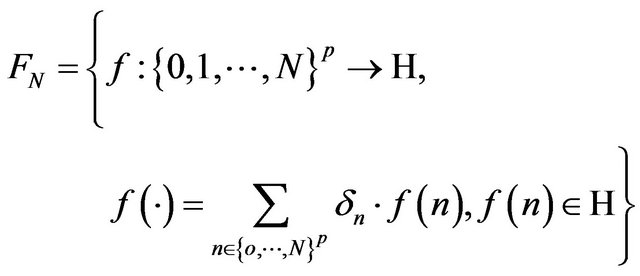
and, for each integer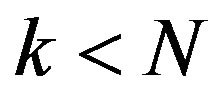 , we denote with
, we denote with
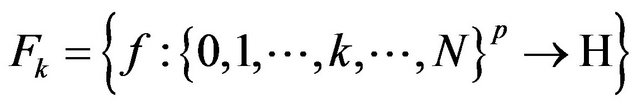
with 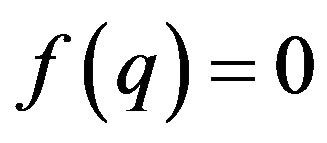 for all multiindices
for all multiindices 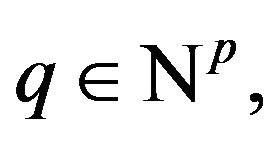 with at least one indices
with at least one indices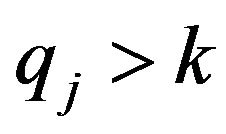 , the C-vector subspaces of
, the C-vector subspaces of 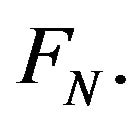 For
For  we also use the same function,
we also use the same function, 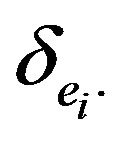 defined by:
defined by:
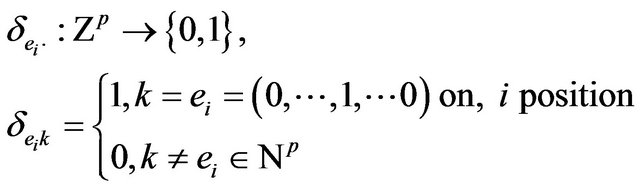
and, for all
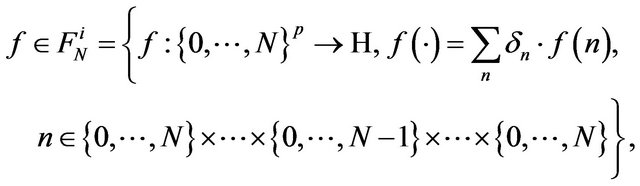
we define the convolutions 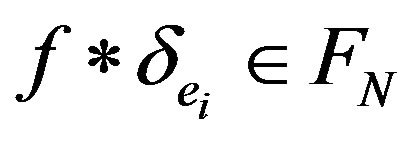 as
as
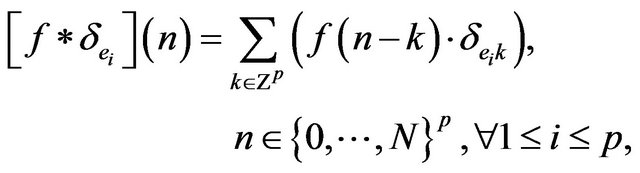
that is 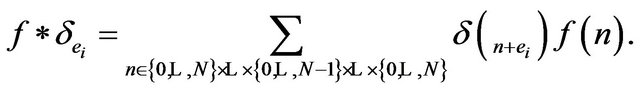
3. Hilbert Spaces Associated with Finite Positive Operator Valued Kernels; Algebraic Prerequisite
We consider for  an operator kernel
an operator kernel
subject on the condition  for all m with
for all m with , acting on a finite dimensional complex vector space H, positively defined. That is the kernel
, acting on a finite dimensional complex vector space H, positively defined. That is the kernel 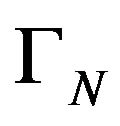 satisfies the condition
satisfies the condition
(A) 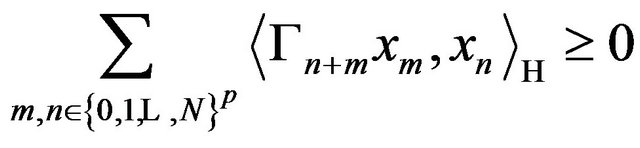
for all sequences  in H. When
in H. When
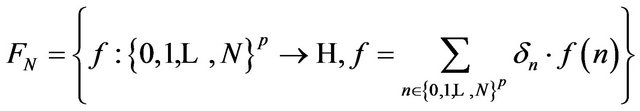
is the C-vector space of functions defined on 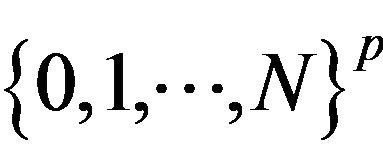 with vectorial values, we consider the kernel
with vectorial values, we consider the kernel  as a double indexed, simmetric one:
as a double indexed, simmetric one:
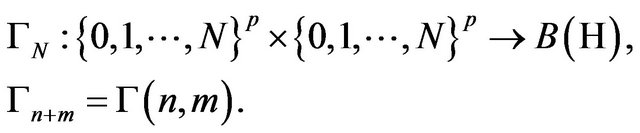
With the aid of , we introduce the hermitian, square positive functional
, we introduce the hermitian, square positive functional
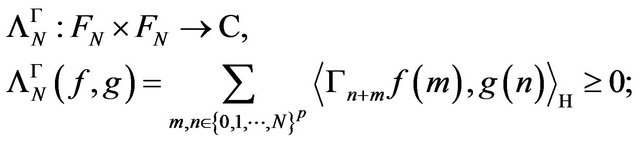
the order in  is the lexicographical one. From property A of the the kernel
is the lexicographical one. From property A of the the kernel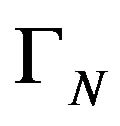 , as well as from the properties of the scalar product in H,
, as well as from the properties of the scalar product in H,  satisfies the conditions:
satisfies the conditions:
1) 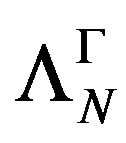 is C-linear in the first argument.
is C-linear in the first argument.
2) , for all
, for all 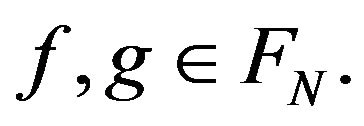
3) , for all
, for all 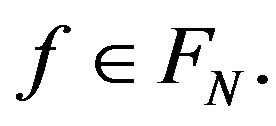
Remarks 3.1.
a) 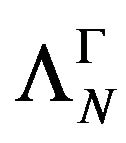 is a hermitian, square, positive functional on
is a hermitian, square, positive functional on 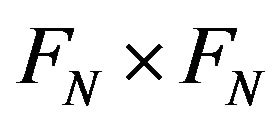 it results that
it results that 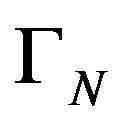 satisfies the Cauchy-Buniakovski-Schwartz inequality, respectively:
satisfies the Cauchy-Buniakovski-Schwartz inequality, respectively:
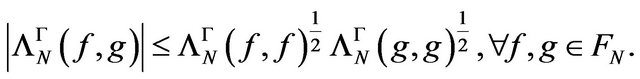
b) Because of the construction of the hermitian functional 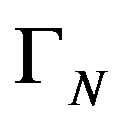 and the simmetry of the kernel
and the simmetry of the kernel 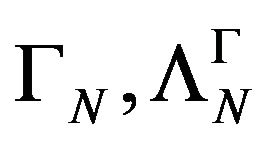 satisfies the equalities:
satisfies the equalities:
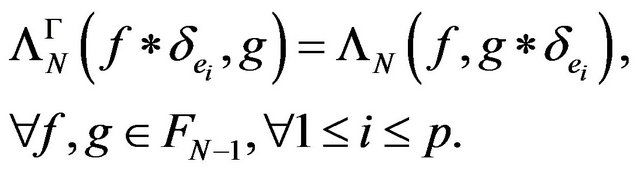
Definition 3.2. A functional 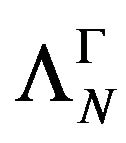 defined on
defined on 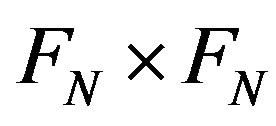 with properties 1)-3) is called a hermitian, square positive functional on
with properties 1)-3) is called a hermitian, square positive functional on .
.
Let  be the subset in
be the subset in , defined as
, defined as 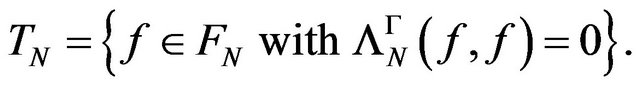 If follows, using the Cauchy-Buniakowski-Schwarz inequality, that if
If follows, using the Cauchy-Buniakowski-Schwarz inequality, that if 
 , we have also
, we have also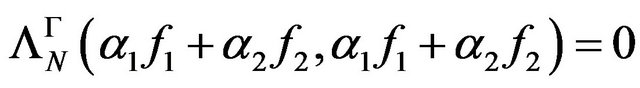 , that is
, that is  is a vector subspace in
is a vector subspace in . The map
. The map
 is a seminorm on
is a seminorm on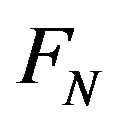 . Because H is a finite dimensional complex vector space,
. Because H is a finite dimensional complex vector space,  is the same. We consider the separated space of
is the same. We consider the separated space of 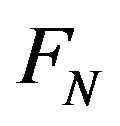 with respect to
with respect to , that is, in this case, the quotient space
, that is, in this case, the quotient space  Obviously, in finite dimensional case for
Obviously, in finite dimensional case for ,
, 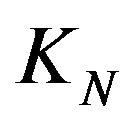 is a finite dimensional Hilbert space with the norm
is a finite dimensional Hilbert space with the norm 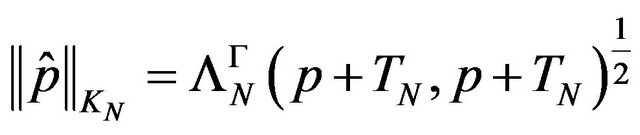 for an arbitrary
for an arbitrary . In the special case of the space
. In the special case of the space
 , we have
, we have
 where
where  represents the class in
represents the class in  of the function
of the function
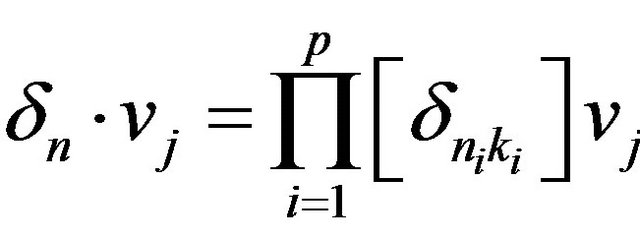
 ,
, 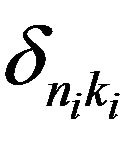
the usual Kroneker symbol, 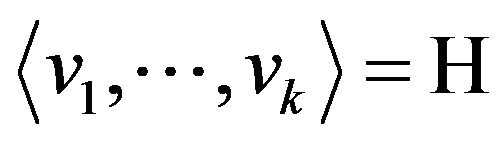 the basis of H and V represents the linear span of these elements. When
the basis of H and V represents the linear span of these elements. When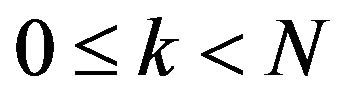 , we consider the vector subspaces
, we consider the vector subspaces , with
, with
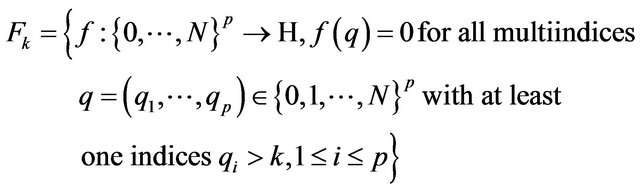
and the restriction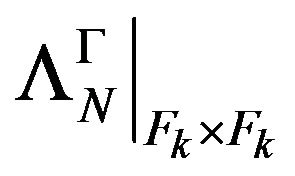 , restriction denoted with
, restriction denoted with
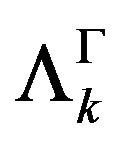 . The functional
. The functional 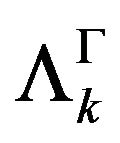 is also a hspf on
is also a hspf on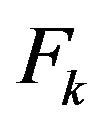 , consequently it has properties 1), 2), 3) and a), b) from Remarks 3.1. Setting
, consequently it has properties 1), 2), 3) and a), b) from Remarks 3.1. Setting
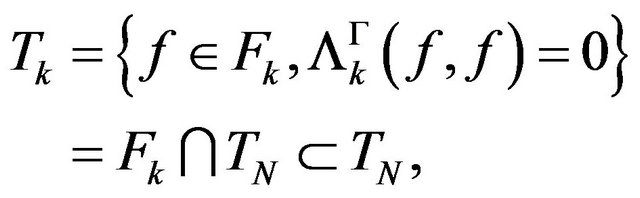
it results that 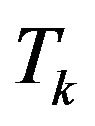 is a vector subspace in
is a vector subspace in 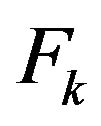 and in
and in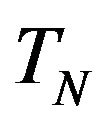 . We denote with
. We denote with 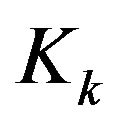 the Hilbert space
the Hilbert space 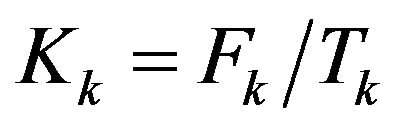 with the norm
with the norm
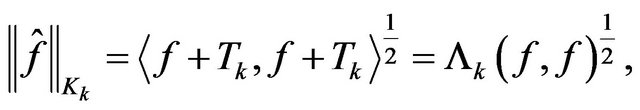
for all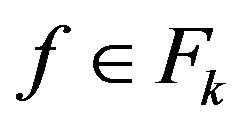 . Because
. Because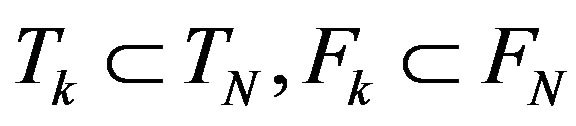 , it results that also
, it results that also  and there is the natural inclusion map
and there is the natural inclusion map
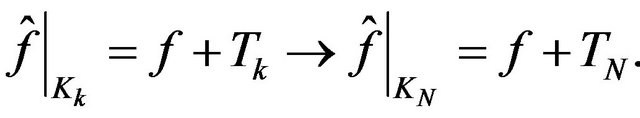
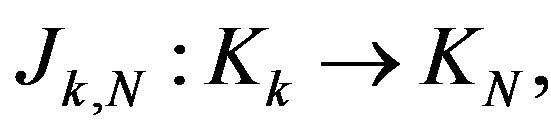 The inclusion map
The inclusion map  is injective one. Indeed, when
is injective one. Indeed, when
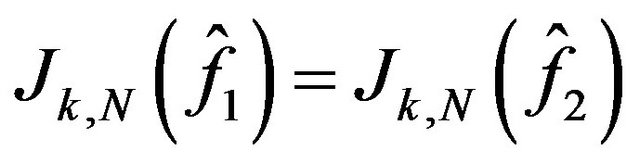 ,
, 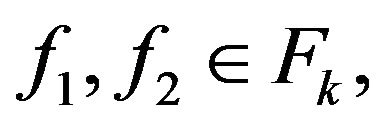 it results
it results 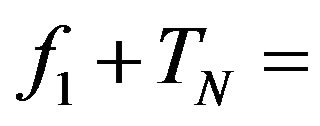
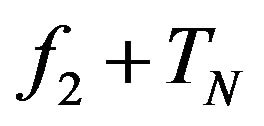 , that is
, that is 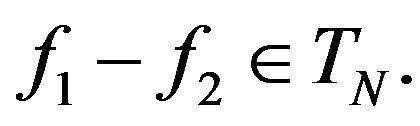 The elements
The elements  are in
are in , consequently
, consequently
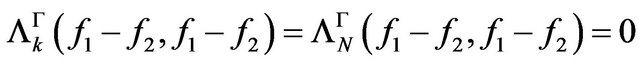 that is
that is 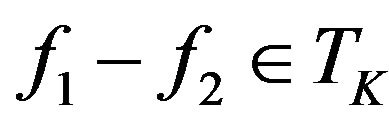 or
or 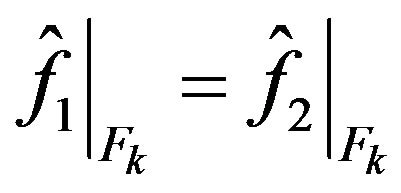 and
and ,
,
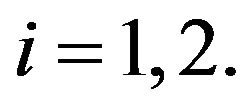 We are interested in conditions in which
We are interested in conditions in which  is an isomorphism of vectorial spaces and
is an isomorphism of vectorial spaces and 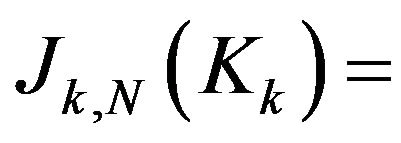
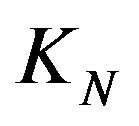 . Because all Hilbert spaces
. Because all Hilbert spaces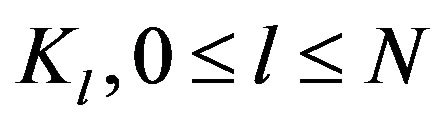 , obtained in this way are finite dimensional, in case
, obtained in this way are finite dimensional, in case  is an isomorphism of vectorial spaces,
is an isomorphism of vectorial spaces, 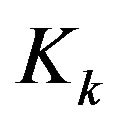 and
and 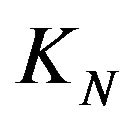 have the same algebraic dimension. In connection with the problem of the stability of the algebraic dimension for the Hilbert spaces obtained as quatient of some vectorialvalued spaces of functions, we are interested in finding operator-valued atomic representing measure for the terms of
have the same algebraic dimension. In connection with the problem of the stability of the algebraic dimension for the Hilbert spaces obtained as quatient of some vectorialvalued spaces of functions, we are interested in finding operator-valued atomic representing measure for the terms of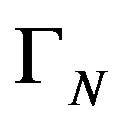 . For such operator-valued, representing atomic measure, the stable number of atoms for the representations of the operators
. For such operator-valued, representing atomic measure, the stable number of atoms for the representations of the operators is the same with that in
is the same with that in 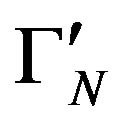 s integral representations. Such studies are the subject of truncated Hausdorff operator-valued moment problems. The concept of stability of the algebraic dimension of the Hilbert space obtained by separating the space of scalar polynomials with finite total degree with respect to an unital square positive functional (the Riesz functional), was introduced in [1]. The concept of stability of the algebraic dimension appears in [1] in the frame of extending some commuting tuple of selfadjoint operators which were intended to get the joint spectral representing measure for the terms of a Hausdorff truncated scalar moment sequences. The concept of stability of the algebraic dimension in [1] is an alternate, geometric aspect of that of “flatness” in Fialkow’s and Curto’s paper [2,3] regarding the truncated scalar moment problems.
s integral representations. Such studies are the subject of truncated Hausdorff operator-valued moment problems. The concept of stability of the algebraic dimension of the Hilbert space obtained by separating the space of scalar polynomials with finite total degree with respect to an unital square positive functional (the Riesz functional), was introduced in [1]. The concept of stability of the algebraic dimension appears in [1] in the frame of extending some commuting tuple of selfadjoint operators which were intended to get the joint spectral representing measure for the terms of a Hausdorff truncated scalar moment sequences. The concept of stability of the algebraic dimension in [1] is an alternate, geometric aspect of that of “flatness” in Fialkow’s and Curto’s paper [2,3] regarding the truncated scalar moment problems.
We adapt and reformulate the concept of stability of the dimension concerning unital square positive functionals on space of scalar polinomyals in [1], to hermitian, square positive functionals associated with positive operator-valued kernels in order to solve operator-valued, truncated, Hausdorff moment problems via Kolmogorov’s theorem of decomposition of such kernels. The problem to obtain operator-valued positive operator representing measure for truncated, trigonometric and Hausdorff operator-valued moment problems via Kolmogorov’s theorem of decomposition of positive operator kernels were solved in [7].
The classical Kolmogorov’s theorem of the decomposition of positive kernels states:
“Let  a nonnegative-definite function where S is a set and H a Hilbert space, namely
a nonnegative-definite function where S is a set and H a Hilbert space, namely
 for any finite number of points
for any finite number of points
 and any vectors
and any vectors . In this case there exists a Hilbert space K (essentialy unique) and a function
. In this case there exists a Hilbert space K (essentialy unique) and a function 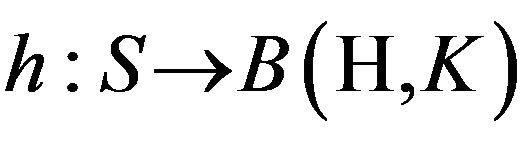 such that
such that  for any
for any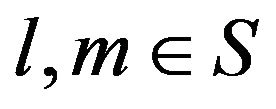 .”
.”
4. Dimension Stability and Consequences in Truncated, Hausdorff, Multidimensional, Operator-Valued Moment Problems
Let 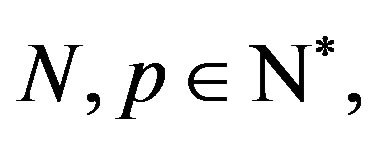
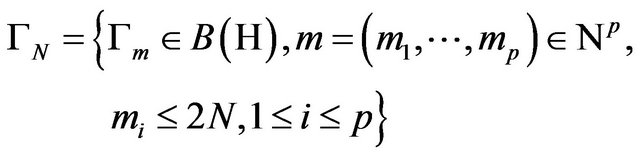
be an operator kernel with  and
and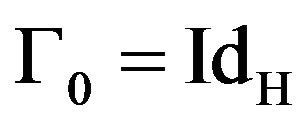 , positively defined, acting on the finite dimensional Hilbert space H, that is
, positively defined, acting on the finite dimensional Hilbert space H, that is 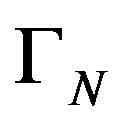 satisfies condition (A) from Section 3; we consider the vector space
satisfies condition (A) from Section 3; we consider the vector space
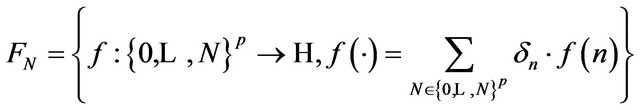
and 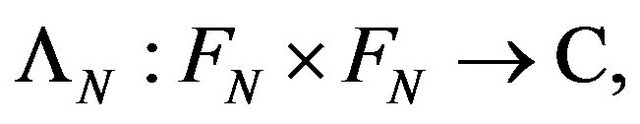
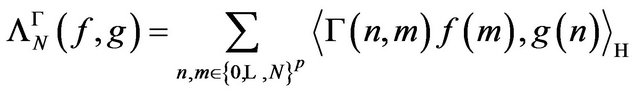 the associated hspf with
the associated hspf with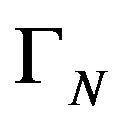 . We consider the set
. We consider the set 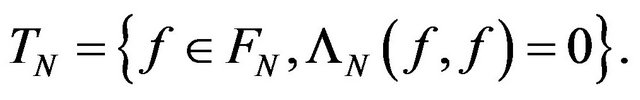 Because
Because  satisfies Cauchy-Buniakovski-Schwarz inequality,
satisfies Cauchy-Buniakovski-Schwarz inequality, 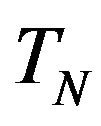 is a vector subspace in
is a vector subspace in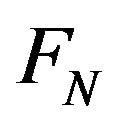 , and also
, and also
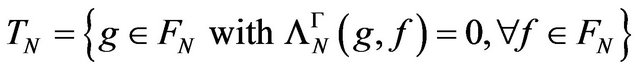
and 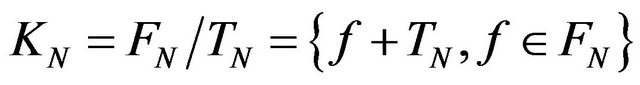 is a finite dimensional Hilbert space, with the norm
is a finite dimensional Hilbert space, with the norm
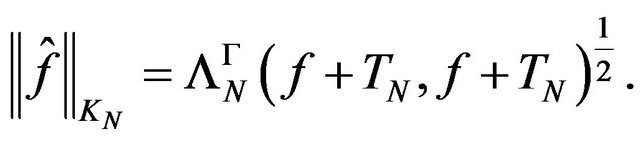 The space
The space  is refered as the Hilbert space obtained via the hspf
is refered as the Hilbert space obtained via the hspf .
.
For every  with
with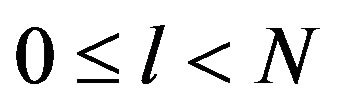 , and
, and
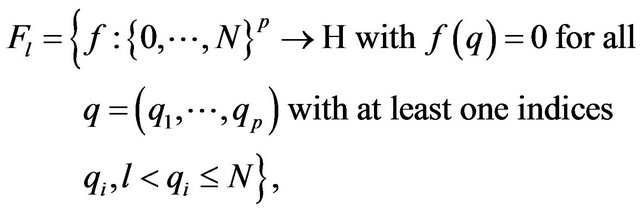
we consider the restriction 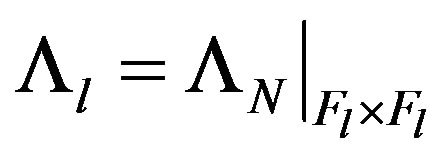 The functional
The functional 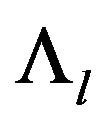 is also a hspf on
is also a hspf on  and satisfies conditions 1), 2), 3) and a), b) in Remark 3.1. The subset
and satisfies conditions 1), 2), 3) and a), b) in Remark 3.1. The subset
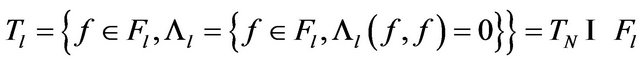
is obviously a subspace in 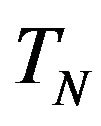 and also in
and also in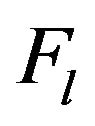 . Consequently, the Hilbert space
. Consequently, the Hilbert space 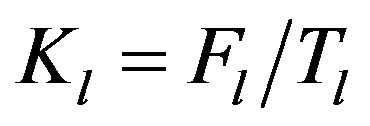 with respect to the norm
with respect to the norm 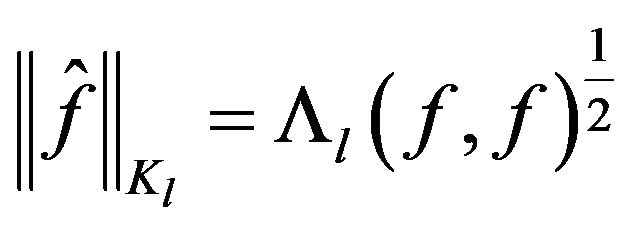 is defined via the hspf
is defined via the hspf 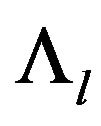
and because  is a vector subspace in TN, the natural inclusion map
is a vector subspace in TN, the natural inclusion map ,
,  ,
,
 for
for  is an isometry. For l = N, we have
is an isometry. For l = N, we have 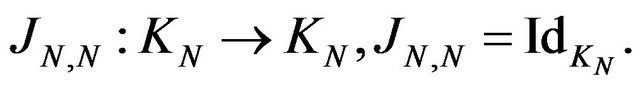 In the same way, for all
In the same way, for all  we have
we have 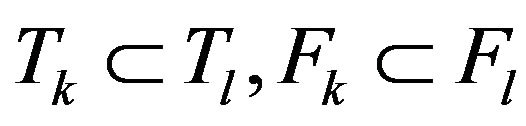 and consequently there exists the naturaly isometries
and consequently there exists the naturaly isometries .
.
If we have an operator-valued kernel 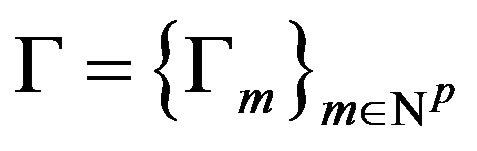 acting on a finite dimensional Hilbert space H, subject on
acting on a finite dimensional Hilbert space H, subject on  for all
for all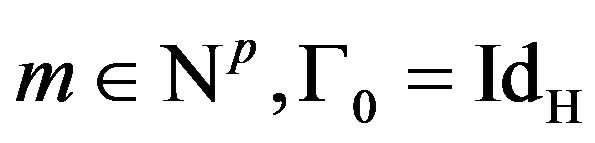 , such that
, such that
 for all sequences
for all sequences 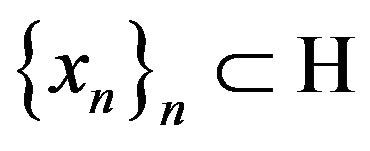
with finite support, considering the vector space
 ,
,
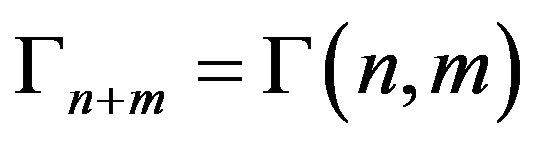 the associated functional
the associated functional
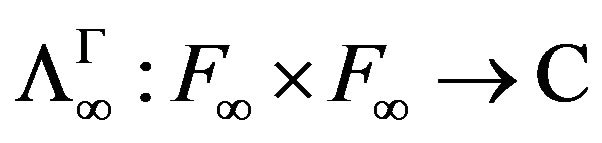 ,
, 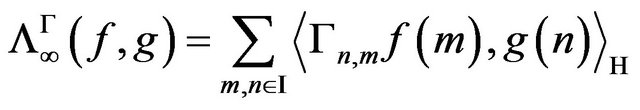 with
with 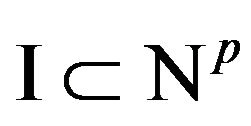 finite, the map
finite, the map  is naturally a hspf on
is naturally a hspf on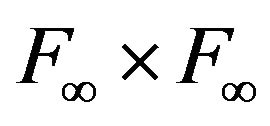 , with properties 1), 2), 3) and a), b) from Remark 3.1. Similar constructions of the Hilbert spaces
, with properties 1), 2), 3) and a), b) from Remark 3.1. Similar constructions of the Hilbert spaces 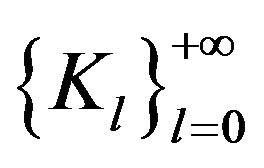 as well as for the isometries
as well as for the isometries 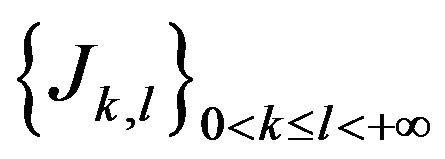 can be done.
can be done.
Definition 4.1. Let 
 ,
, 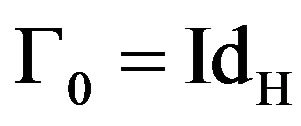
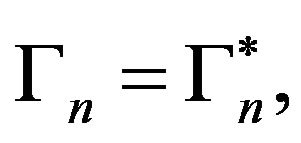
 be a positive definite kernel,
be a positive definite kernel,  the hspf associated with
the hspf associated with  and
and  the Hilbert spaces built via
the Hilbert spaces built via  and
and 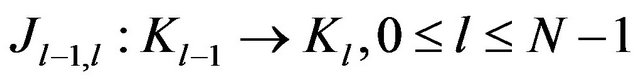 the associated isometries. If for some
the associated isometries. If for some 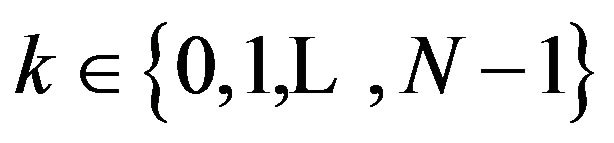 the injective map
the injective map  is also surjective, that is
is also surjective, that is  we say that
we say that 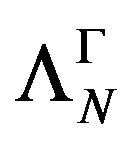 and the kernel
and the kernel 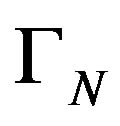 is dimensionally stable (stable) at k.
is dimensionally stable (stable) at k.
The kernel 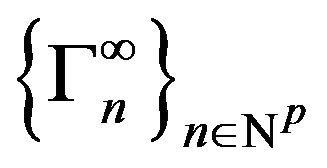 is called dimensionally stable if there exists integers
is called dimensionally stable if there exists integers 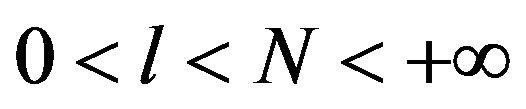 such that the kernel
such that the kernel 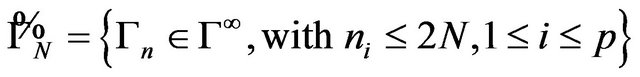 is stable at
is stable at 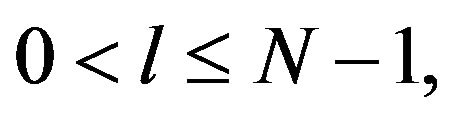 respectively
respectively 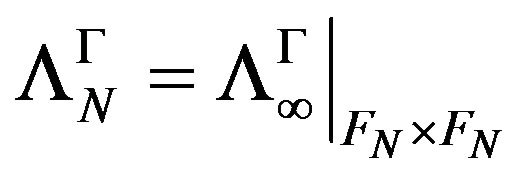 is stable at l.
is stable at l.
Remark 4.2. c) Let ,
, 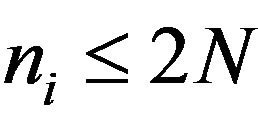 , be a positive definite kernel,
, be a positive definite kernel, 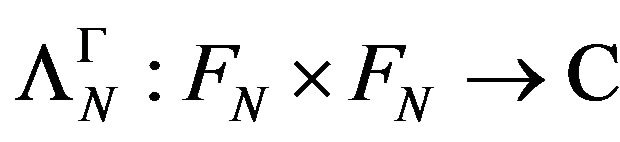 the hspf associated with
the hspf associated with 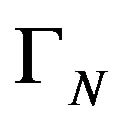 stable at
stable at  and
and  the Hilbert spaces built via
the Hilbert spaces built via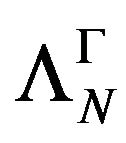 ; (
; ( are bijective maps,
are bijective maps,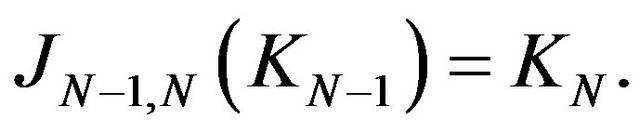 ) In this case, the maps
) In this case, the maps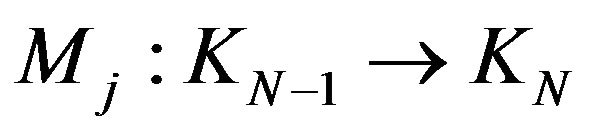 ,
,
 when
when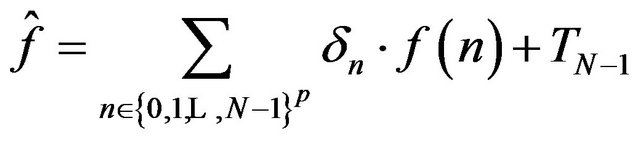 , and
, and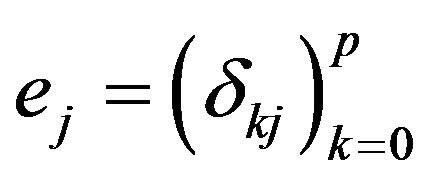 for all
for all  are correctely defined.
are correctely defined.
Indeed, let  be such that
be such that
 ; we shall prove that
; we shall prove that  If
If
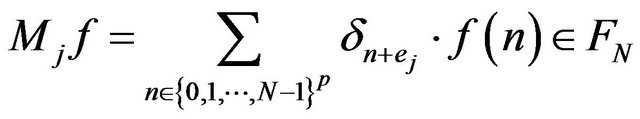 and
and  is stable at
is stable at
 ,
, 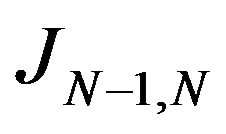 is an isomorphism of vectorial spaces, exists then
is an isomorphism of vectorial spaces, exists then  such that
such that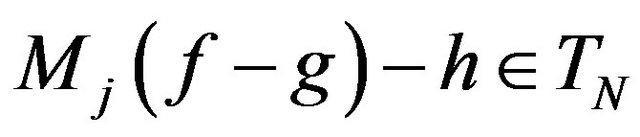 . In this case, using property a) and b) in Remarks 3.1 for the kernel
. In this case, using property a) and b) in Remarks 3.1 for the kernel  we have:
we have:
 (4)
(4)
Also, using the Cauchy-Schwartz inequality,
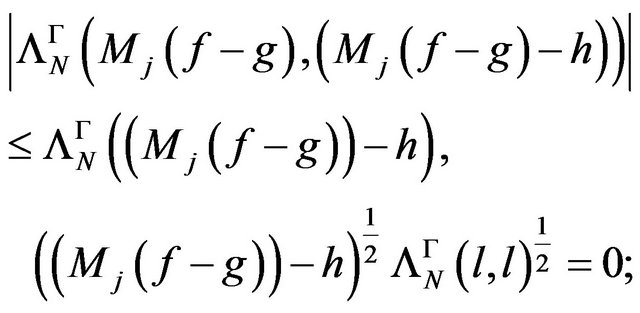 (5)
(5)
where we have denoted with .
.
From (4), (5), we have:
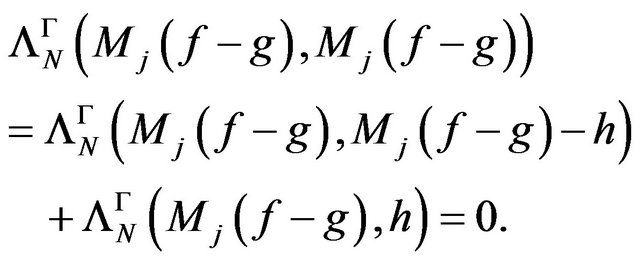
It results, that 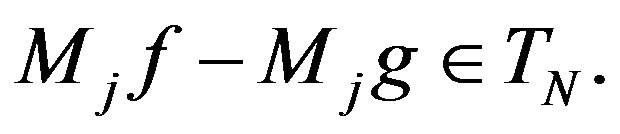 The maps
The maps
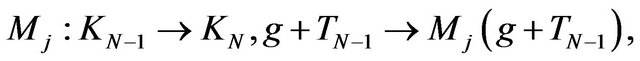

are correctely defined.
d) If we consider the subspaces
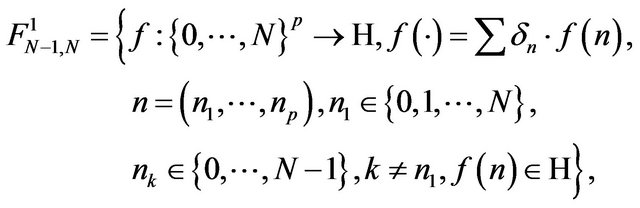
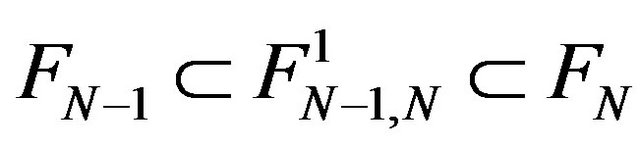 , also
, also  the null spaces
the null spaces
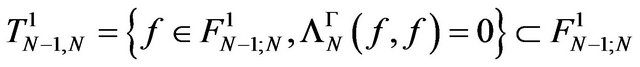
of it. We have
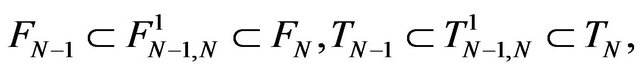
it results,
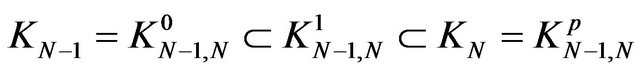 .
.
The same
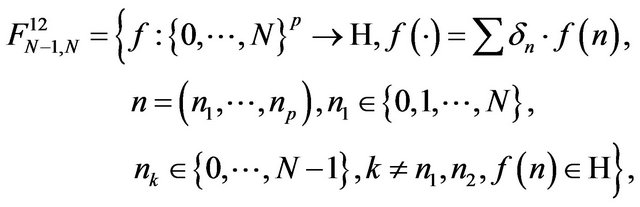
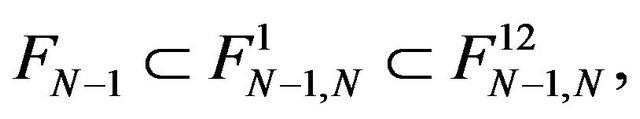 and the null subspace
and the null subspace
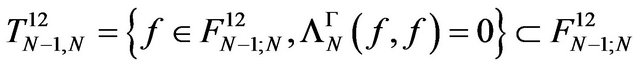
of it. We have also  for the Hilbert quotient spaces we obtain
for the Hilbert quotient spaces we obtain
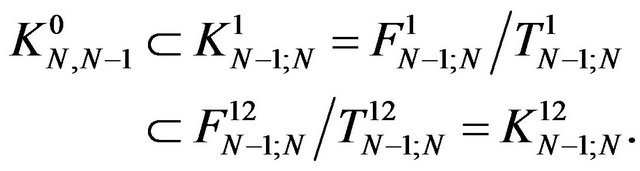
In the same way, by recurrence, we obtain the vectorial subspaces
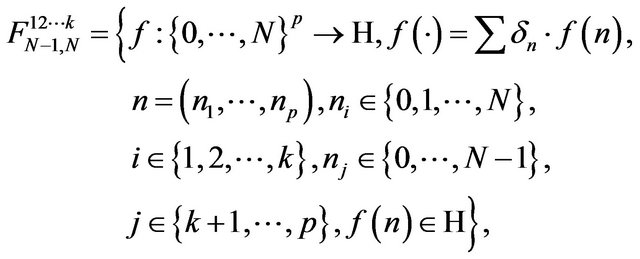
the null subspaces
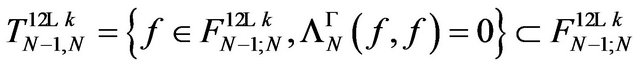
of it and the required quotient Hilbert space
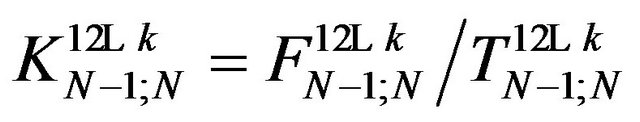 for all
for all  From the above construction, the inclusions of the Hilbert spaces
From the above construction, the inclusions of the Hilbert spaces
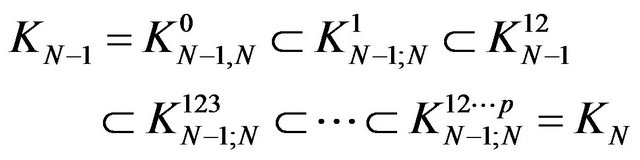
and the naturally isometries
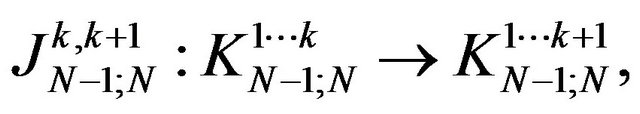
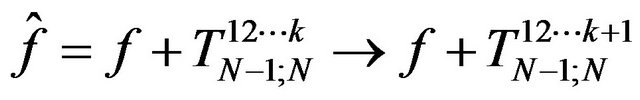
are obtained, for all 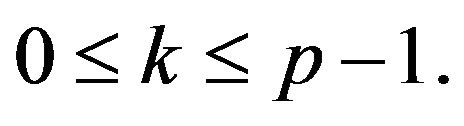 Because
Because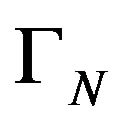 , respectively
, respectively 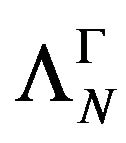 are stable at
are stable at , it results
, it results
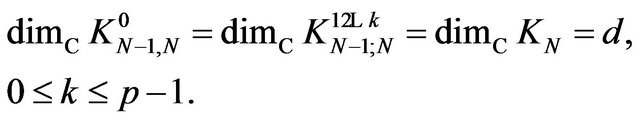
Consequently all the isometries 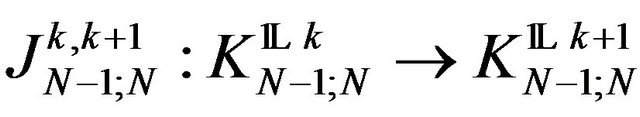 are surjective one. Let as consider the operators:
are surjective one. Let as consider the operators:
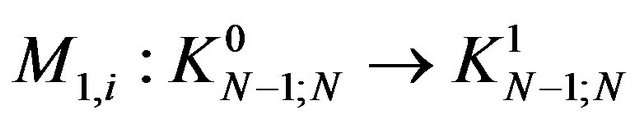 ,
,
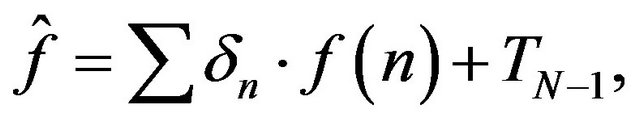
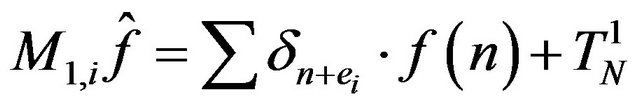
and
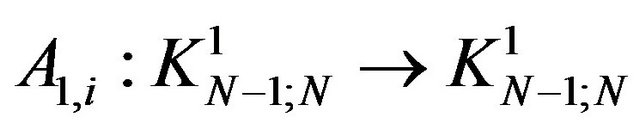
by
 .
.
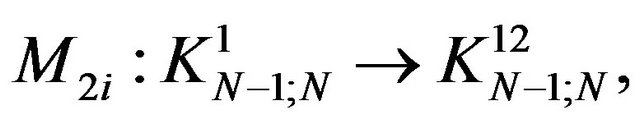
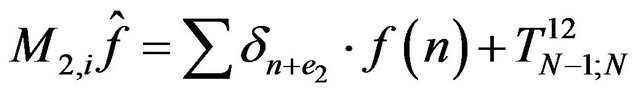
and
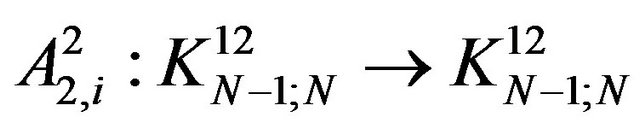
by . By recurrence the operators
. By recurrence the operators
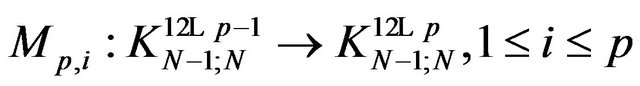
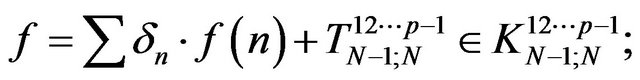
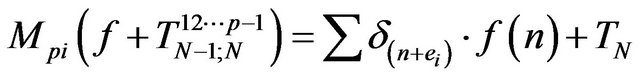
and
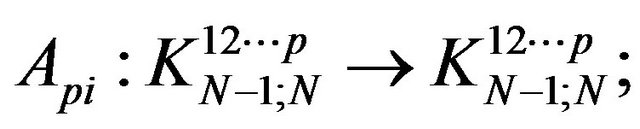
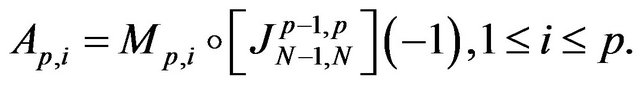
From the construction, immediately, it follows that
 (6)
(6)
The operators 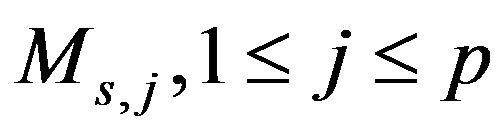 are correctely defined.
are correctely defined.
Indeed, let  we show that also
we show that also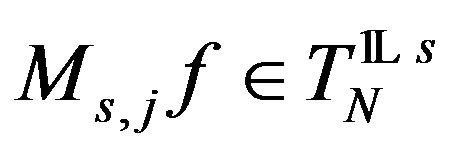 ; from the stability condition, it exists
; from the stability condition, it exists 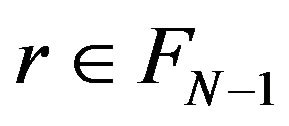 such that
such that  and, from CauchyBuniakovski-Schwartz and property b) of the kernel
and, from CauchyBuniakovski-Schwartz and property b) of the kernel , we have:
, we have:
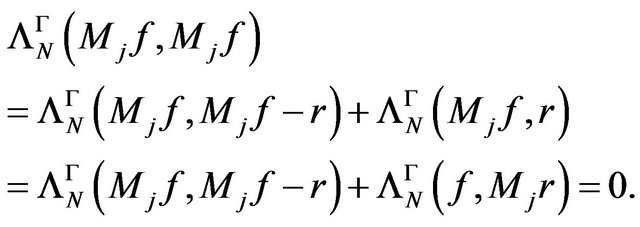
That is the operators 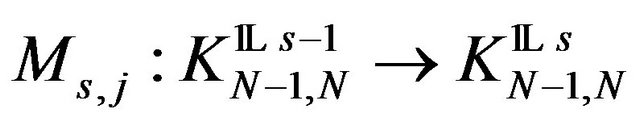 are correctly defined. and extend the operators
are correctly defined. and extend the operators  to
to 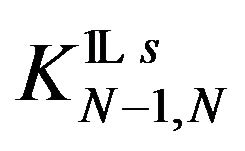 We apply (6) for computing
We apply (6) for computing
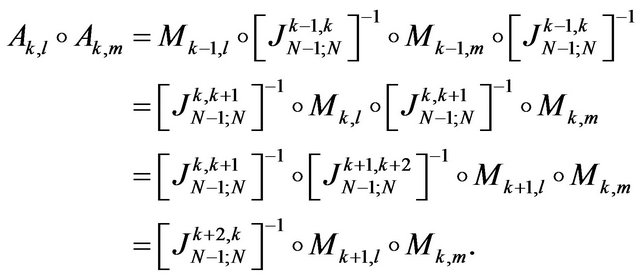
Consequently, it results
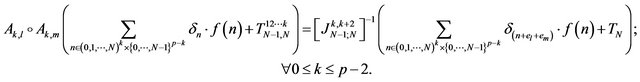 (7)
(7)
where we have denoted
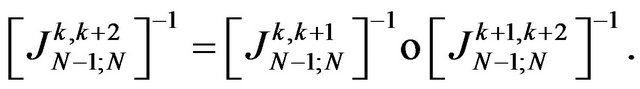
e) We consider the maps 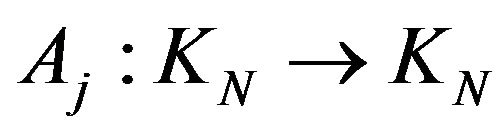 defined by
defined by  for
for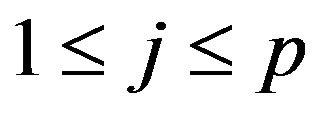 . With
. With  the given isomorphism of vectorial spaces in case of
the given isomorphism of vectorial spaces in case of , stable at
, stable at  and with
and with , the linear operators
, the linear operators  in c), the obtained
in c), the obtained 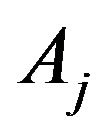 operators are linear, correctely defined too.
operators are linear, correctely defined too.
Proposition 4.3. The linear operators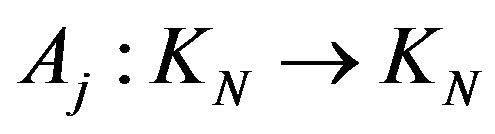 ,
, 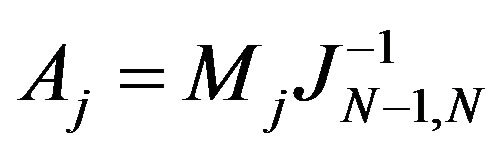 ,
,  are selfadjoin on
are selfadjoin on 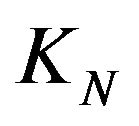 and the tuple
and the tuple 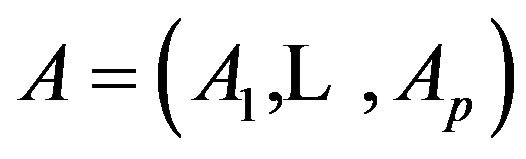 is a commuting multioperator on
is a commuting multioperator on .
.
Proof. From Remark 4.1. e) The operators 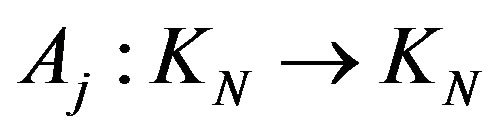 ,
,  are linear, correctely defined on the Hilbert space
are linear, correctely defined on the Hilbert space . We show that
. We show that  are selfadjoint one and commute; that is we verify
are selfadjoint one and commute; that is we verify
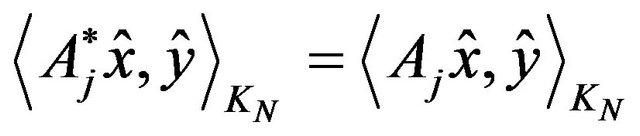 and
and 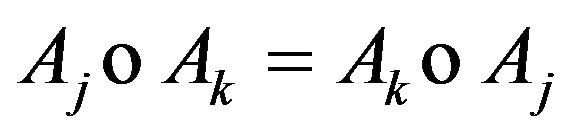 for all
for all
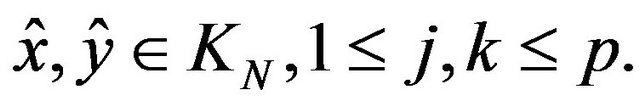 Let
Let 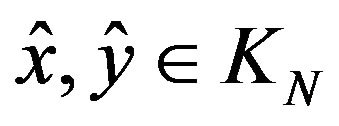 arbitrary,
arbitrary,
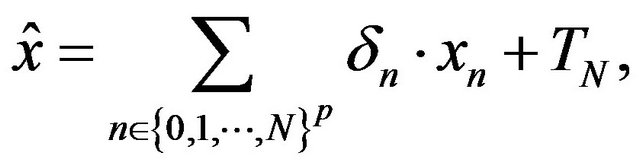
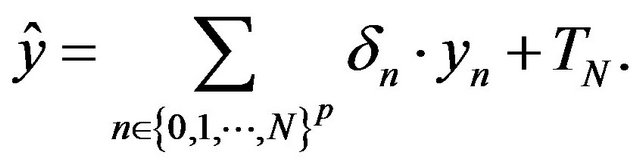
From the stability of  and
and 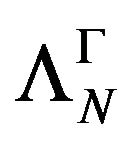 at
at ,
,  is an isomorphism of vectorial spaces; it results that there exist
is an isomorphism of vectorial spaces; it results that there exist
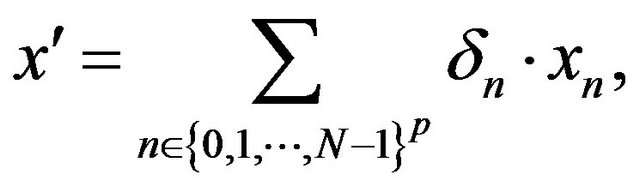
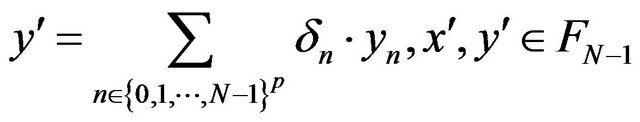
with 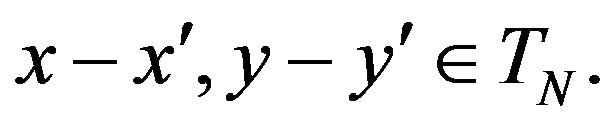
We have
 (8)
(8)
where we have denoted by 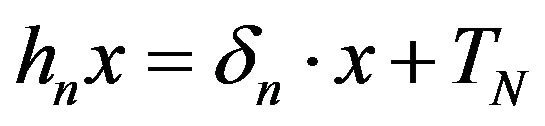 (the class of
(the class of  with respect to
with respect to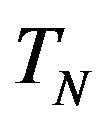 . The last statement is due to Kolmogorov’s theorem of decomposition of positive kernels.
. The last statement is due to Kolmogorov’s theorem of decomposition of positive kernels.
We have also,
 (9)
(9)
From (8) and (9), it results that 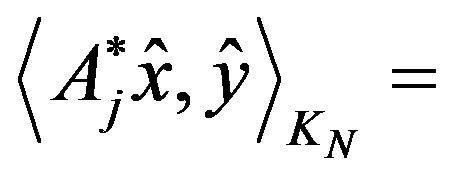
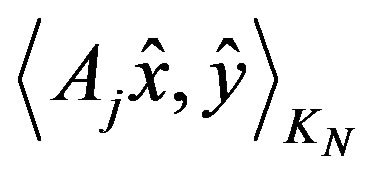 for all
for all 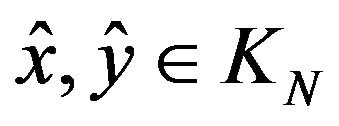 that is
that is 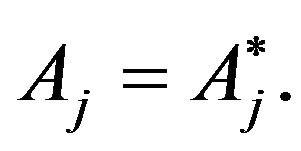
Commutativity. We shall prove that 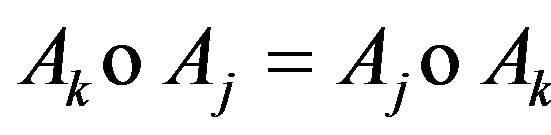 for all
for all 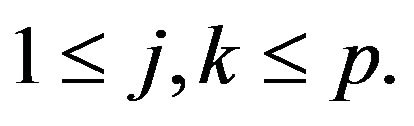 Following
Following  definitions, it is sufficient to verify in this order that
definitions, it is sufficient to verify in this order that
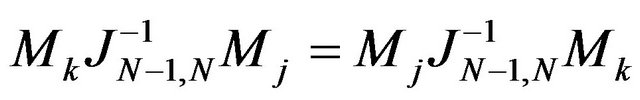 for all
for all . Let
. Let
 be the vectorial function
be the vectorial function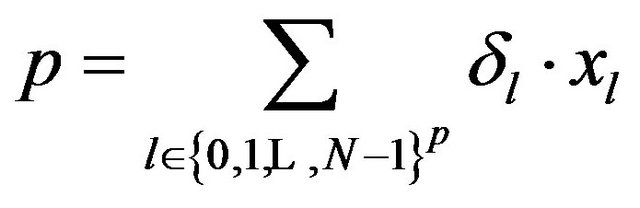 , we have:
, we have:
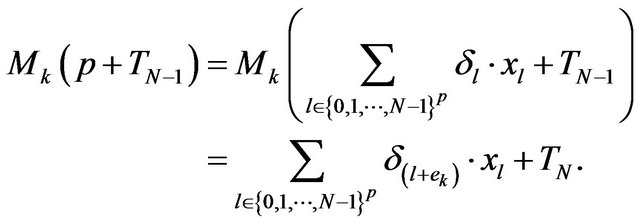
Because 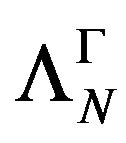 is stable at
is stable at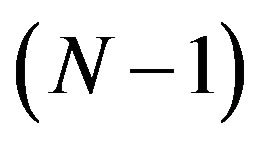 ,
, 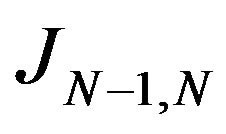 is an isomorphism of vectorial spaces, it exists
is an isomorphism of vectorial spaces, it exists
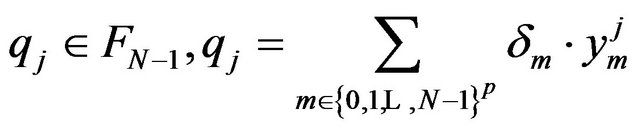 such that:
such that:
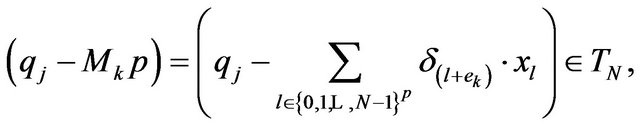
case in which
 (10)
(10)
We compute also
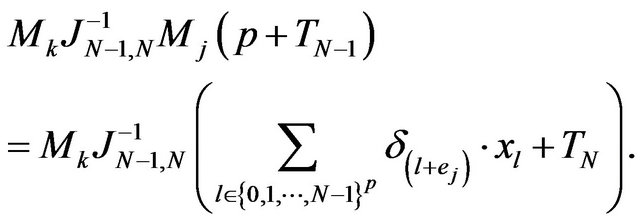
Because 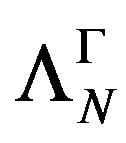 is stable at
is stable at ,
, 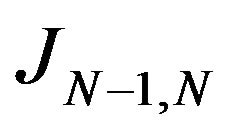 is an isomorphism, it exists
is an isomorphism, it exists  such that
such that 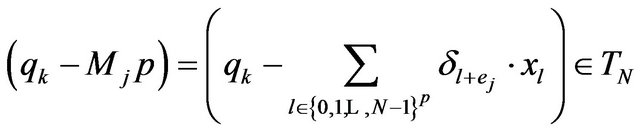 and
and
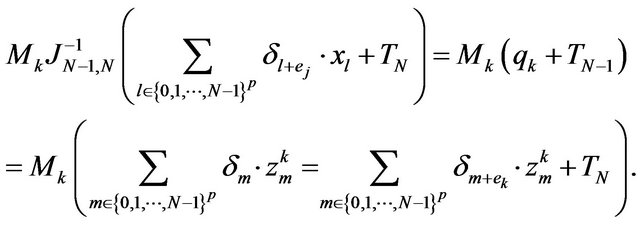 (11)
(11)
We prove that results in (10), (11) are equal; that is:
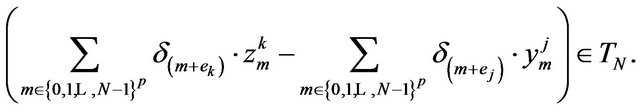
Indeed, let us consider the element
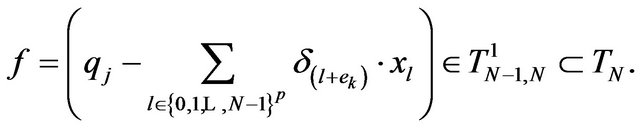
In these conditions, we can define 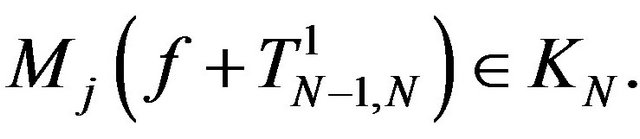 Because
Because 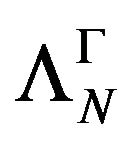 is stable at
is stable at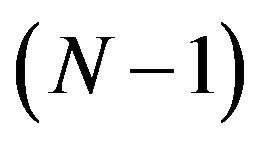 , we can find
, we can find 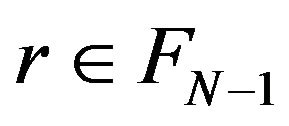 such that
such that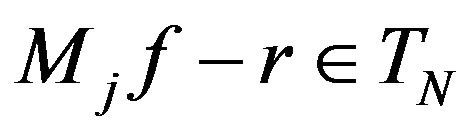 . In these conditions, from Cauchy-Buniakowski-Schwartz inequality and property b) in Remark 3.1,
. In these conditions, from Cauchy-Buniakowski-Schwartz inequality and property b) in Remark 3.1,
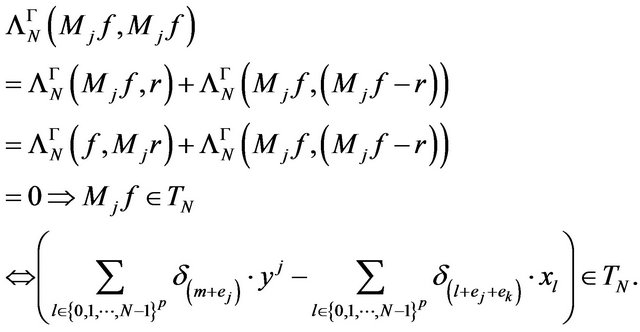 (12)
(12)
Similarly, if we denote with
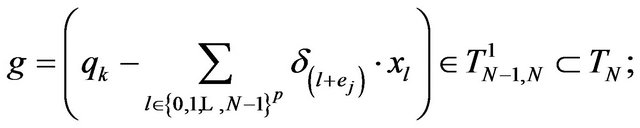
we can define the extension
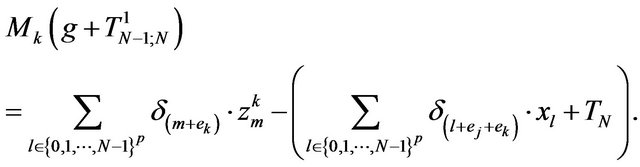
From the stability of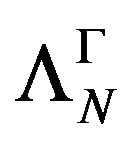 , respectively
, respectively 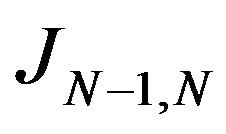 is an isomorphism, it exists
is an isomorphism, it exists 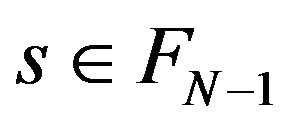 with
with 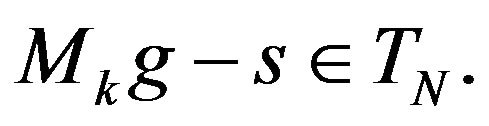 From the same calculation as previous,
From the same calculation as previous,
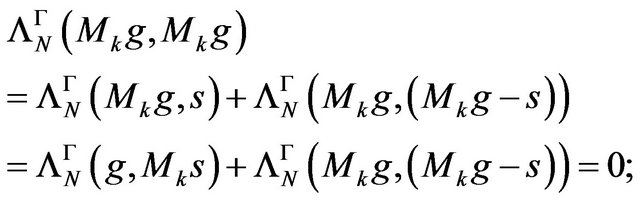
that is  Consequently, we have:
Consequently, we have:
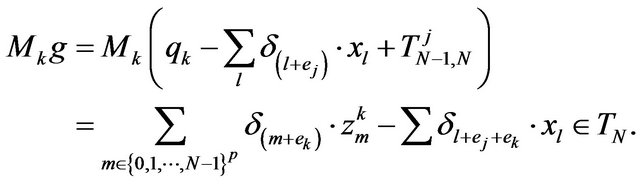 (13)
(13)
From (12) and (13),
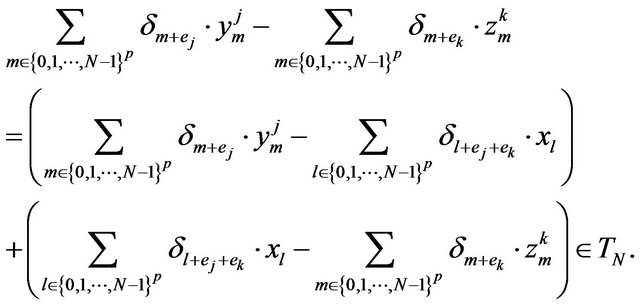
That is results in (10) and (11) are equal; commutativity occurs. 
Remark 4.4. In conditions of Proposition 4.3, we have  for all
for all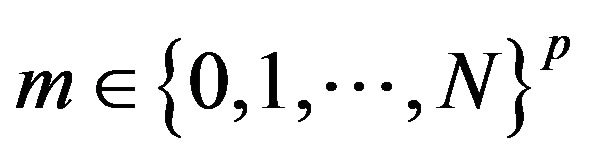 ,
,  where
where  stands for
stands for , respectively
, respectively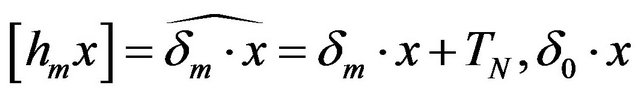 ,
, 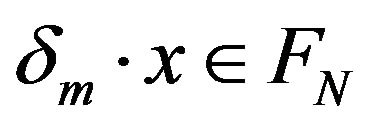
and 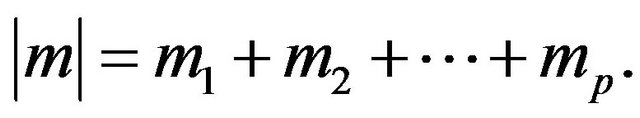
Proof. Indeed, because  is stable at
is stable at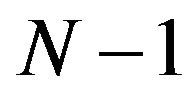 , if
, if , from the definition of
, from the definition of
 we have
we have
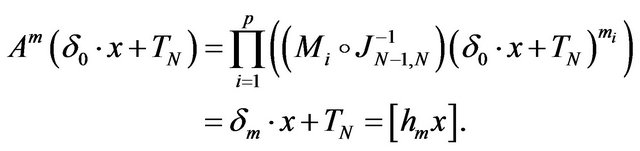
Let 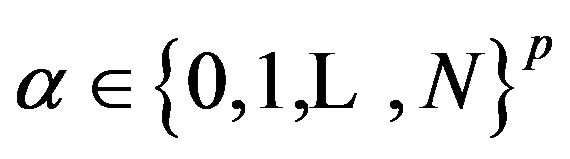 with
with  we consider
we consider 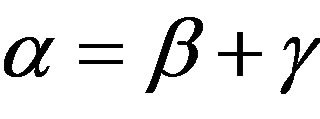 with
with 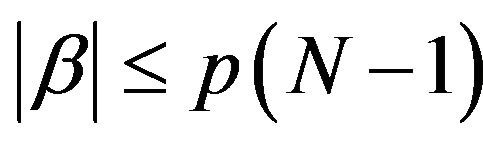 and
and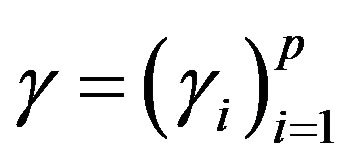 ,
,  or
or . In this case, from Remark 4.2 d) and first assertion of above,
. In this case, from Remark 4.2 d) and first assertion of above,
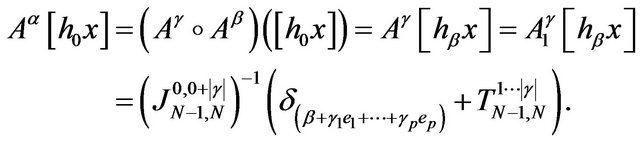
From the definitions of the isomorphisms ,
,  , it results
, it results
 ;
;
that is
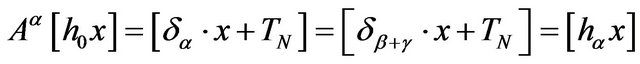
for all 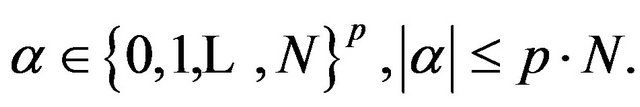
Theorem 4.5. Let
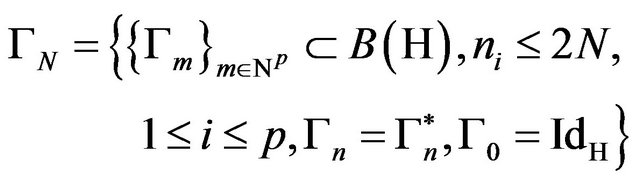
with the property 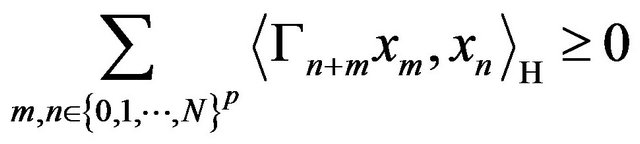 for any sequences
for any sequences  Let
Let 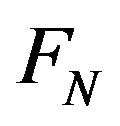 the vector space of vectorial functions and
the vector space of vectorial functions and  the hspf associated with
the hspf associated with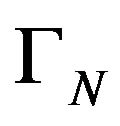 , as in Remark 3.1, stable at
, as in Remark 3.1, stable at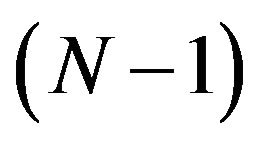 . Then there exists a unique extension
. Then there exists a unique extension  of
of 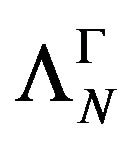 which is a hspf on
which is a hspf on  and has property b) in Remark 3.1.
and has property b) in Remark 3.1.
Proof. From Proposition 4.1, with the same notations as in Section 3, using the stability of  at
at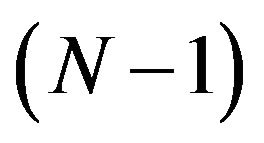 , we can define a p commuting tuple of selfadjoint operators
, we can define a p commuting tuple of selfadjoint operators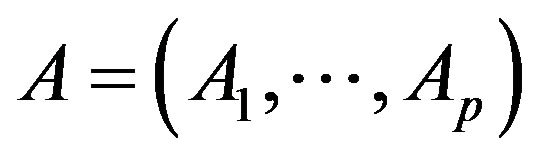 ,
,  ,
, . For an arbitrary
. For an arbitrary 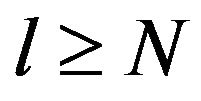 and
and , we define the element
, we define the element
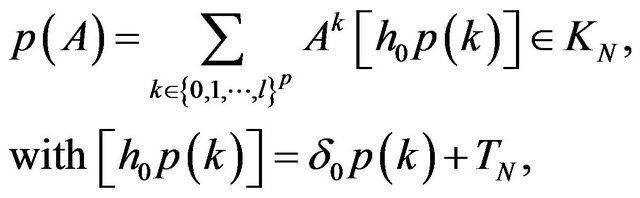
when 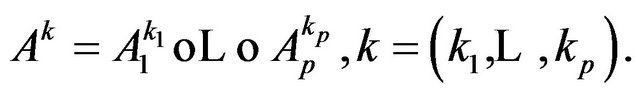 Let us consider the functional
Let us consider the functional  defined by
defined by 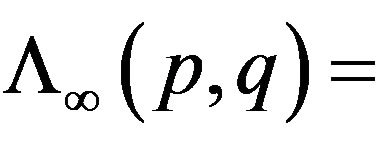
 when
when  with
with  arbitrary.
arbitrary.
We prove in the sequel that  is an extension of
is an extension of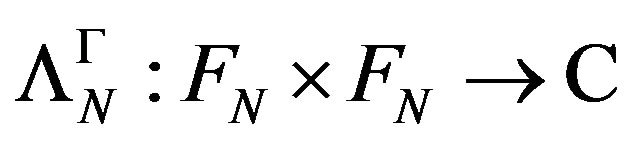 , it is a hspf on
, it is a hspf on 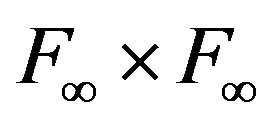 and it has property b) in Remark 3.1.
and it has property b) in Remark 3.1.
From the properties of the scalar product on 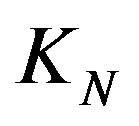 and definition of
and definition of 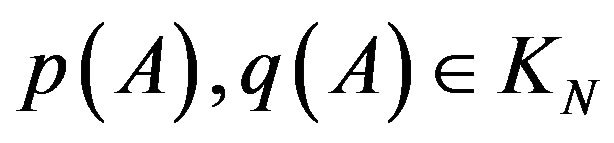 above, we have
above, we have
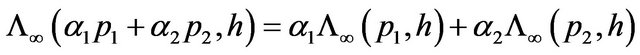
for all  arbitrary. Obviously, using the same properties, we have:
arbitrary. Obviously, using the same properties, we have:
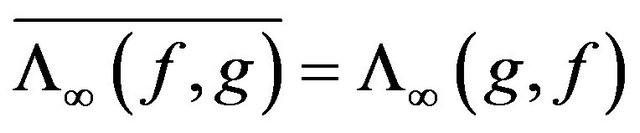 and
and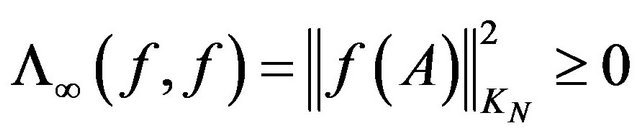 ,
, 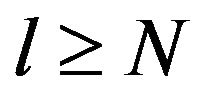 ,
, 
arbitrary. It results that  is a hspf on
is a hspf on .
.
We verify that 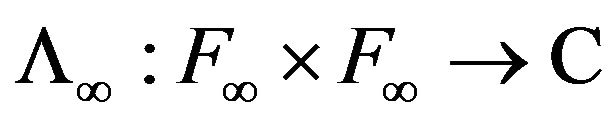 is an extension of
is an extension of  For any vector-valued functions
For any vector-valued functions
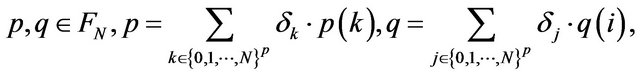
we have:
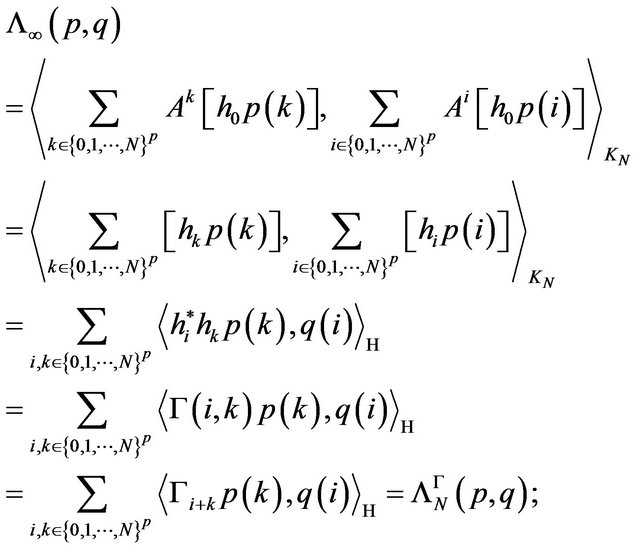
that is 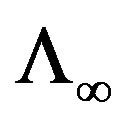 is an extension as hspf to
is an extension as hspf to 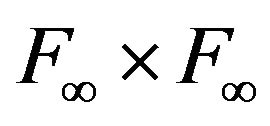 of
of  (the above results uses Remark 4.4 and Kolmogorov’s theorem).
(the above results uses Remark 4.4 and Kolmogorov’s theorem).
We verify that  has also property b) in Remark 3.1, respectively it fullfiels
has also property b) in Remark 3.1, respectively it fullfiels
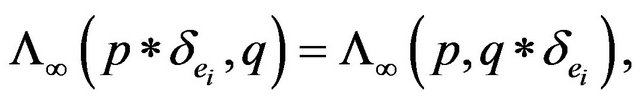
for all 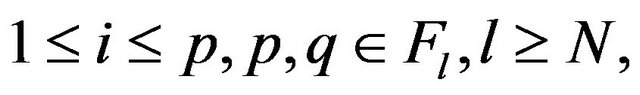 arbitrary. Indeed,
arbitrary. Indeed,
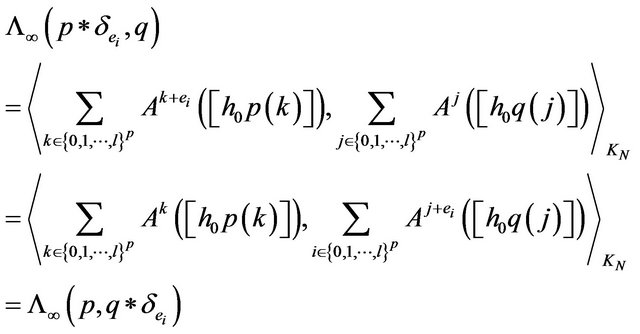
the required property. We prove that  is the unique extension of
is the unique extension of 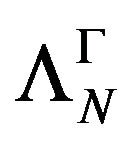 with the mentioned properties. Suppose that
with the mentioned properties. Suppose that  are two extensions to
are two extensions to  of
of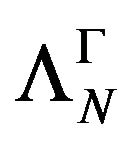 , both of them with the specified properties. We prove by recurrence, that for every
, both of them with the specified properties. We prove by recurrence, that for every  and any vectorial function
and any vectorial function , there exists
, there exists  such that
such that 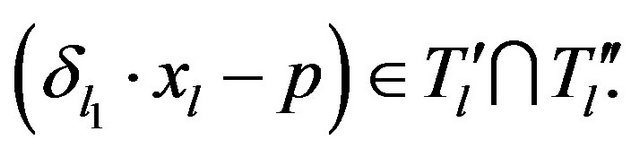 For
For 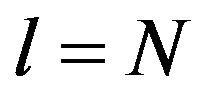 and
and , because
, because 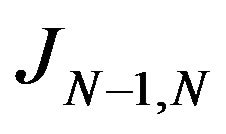 is an isomorphism, exists then an element
is an isomorphism, exists then an element  such that
such that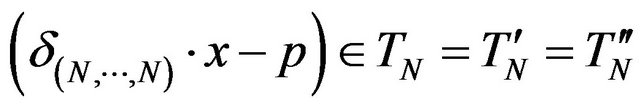 ; that is the required assertion, in case
; that is the required assertion, in case , is true. We consider the statement satisfied in case
, is true. We consider the statement satisfied in case 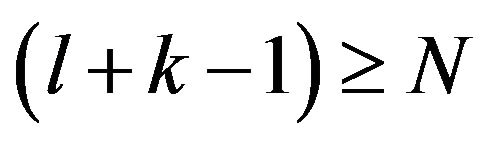 and prove it for
and prove it for 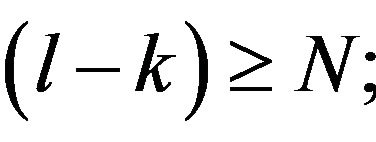 that is for any
that is for any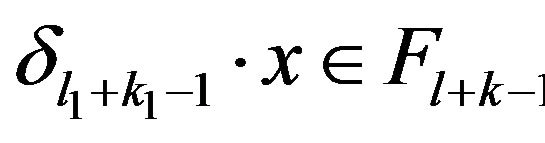 , with
, with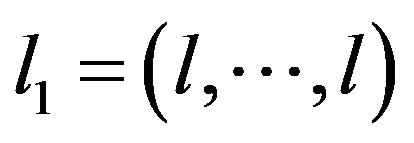 ,
,  , there is an element
, there is an element ,
, 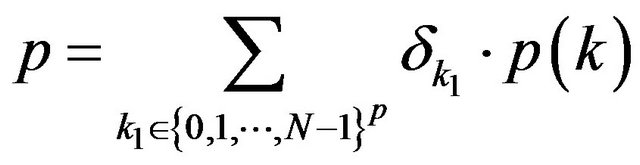 such that
such that
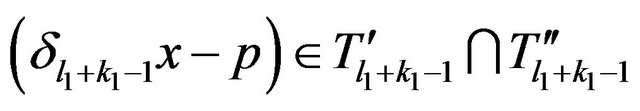 . This relation means that
. This relation means that
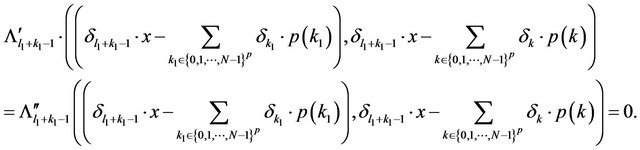
We compute:
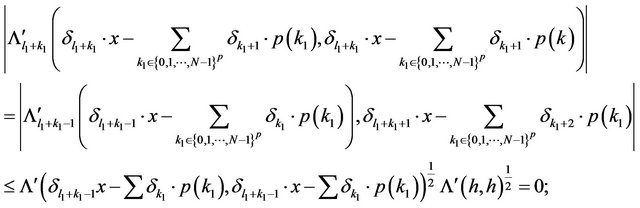
where we have denoted with:
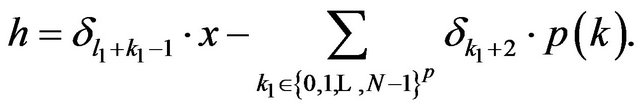
The same inequality is true for ; it results that
; it results that
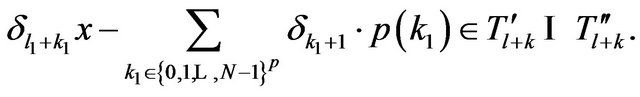
The vectorial function
 ,
, 
is an isomorphism ( is stable at
is stable at ), there exists
), there exists  such that
such that
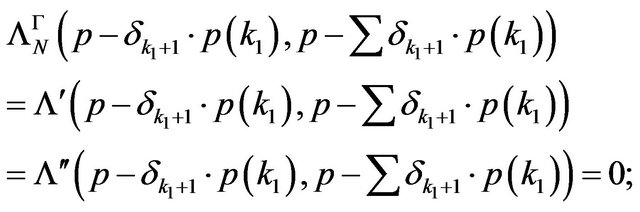
that is  We have:
We have:
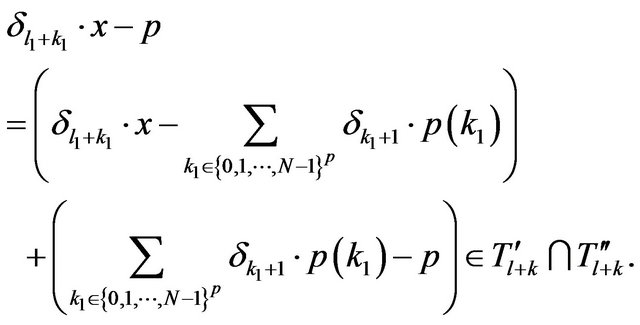
For every , and any
, and any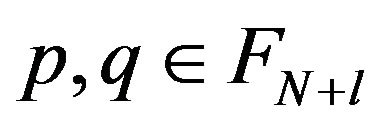 , it results, from above, that we can find the elements
, it results, from above, that we can find the elements 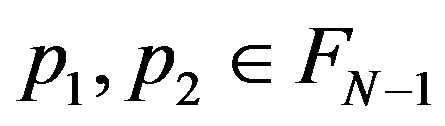 such that
such that  Moreover,
Moreover,
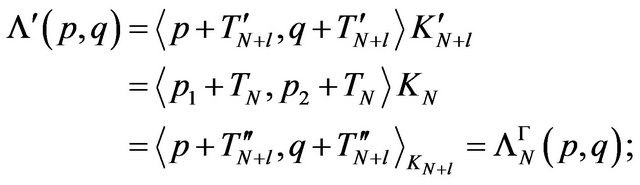
showing that 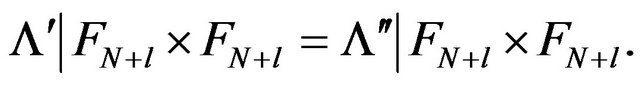 The integer
The integer  is arbitrary choosen, we obtain that
is arbitrary choosen, we obtain that
 ; that is the extension with such properties is unique.
; that is the extension with such properties is unique. 
Remark 4.6. Let 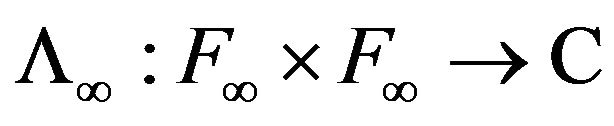 be defined by
be defined by
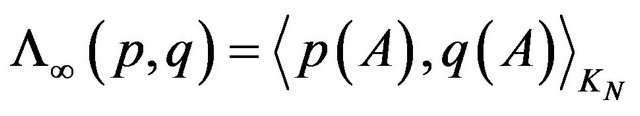 , for any
, for any .
.
In this case, the null space is
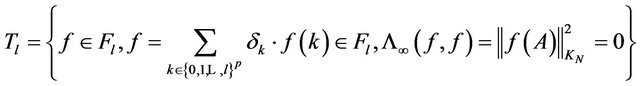 .
.
It results that, for any  there exists
there exists  such that
such that ; we prove that
; we prove that 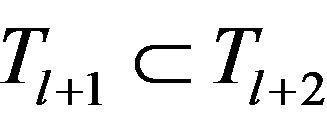 for any
for any .
.
Let 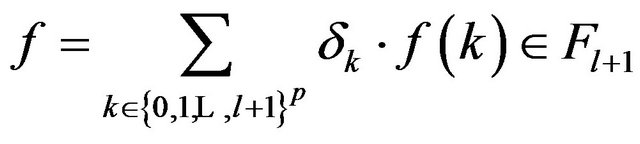 such that
such that
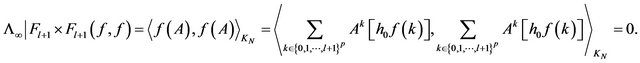
 , it follows
, it follows
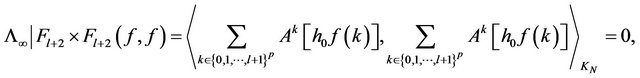
that is  for any
for any  consequently,
consequently,  for any
for any 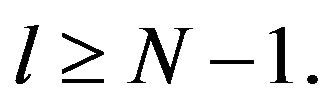
Proposition 4.7. Let  be an operator kernel, positively defined and
be an operator kernel, positively defined and  the hspf associated with the kernel
the hspf associated with the kernel 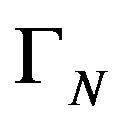 as previous, stable at
as previous, stable at  and
and 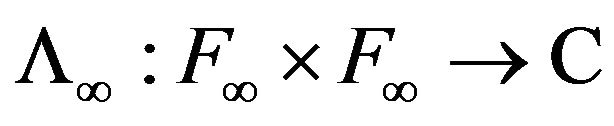 , the unique extension of
, the unique extension of  to
to  as hspf and property b) in Remark 3.1. Then
as hspf and property b) in Remark 3.1. Then 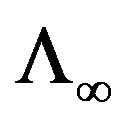 is stable at any
is stable at any 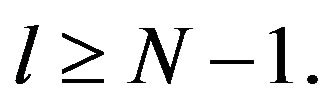
Proof. Let 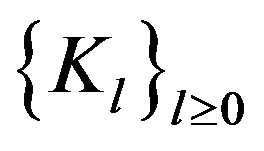 be the Hilbert spaces built via
be the Hilbert spaces built via  and
and 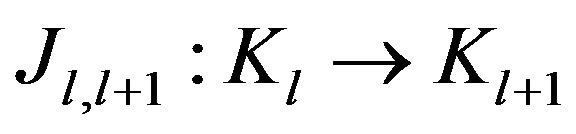 be the associated isometries. We prove, by induction, that
be the associated isometries. We prove, by induction, that  for all
for all  The assertion is true for
The assertion is true for 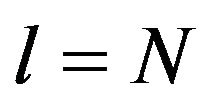 (
( is an isomorthism,
is an isomorthism,  is stable at N). Assume that the assertion is true for some
is stable at N). Assume that the assertion is true for some 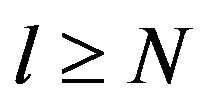 and prove it for
and prove it for  We fix an element
We fix an element 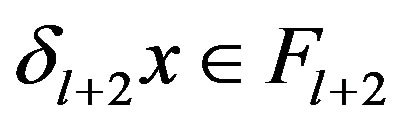 and prove thatwe can find an element
and prove thatwe can find an element 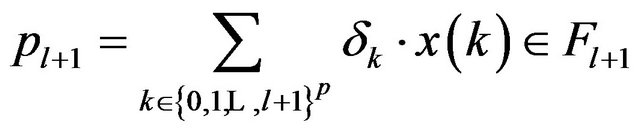
such that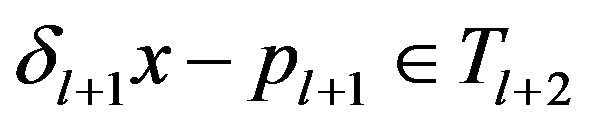 , with
, with  the null space of
the null space of 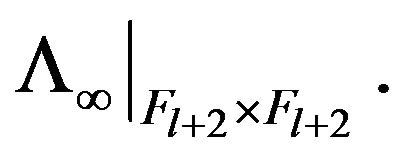 For the element
For the element 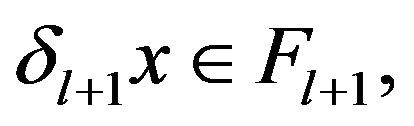 because
because 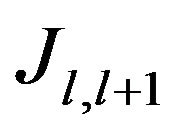 is an isomorphism, it exists then
is an isomorphism, it exists then
 such that
such that
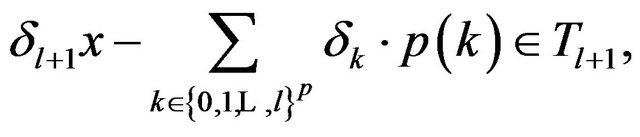 that is
that is
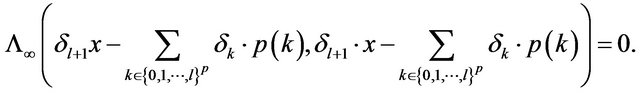
Using the property b) in Remark 3.1 for , we compute:
, we compute:
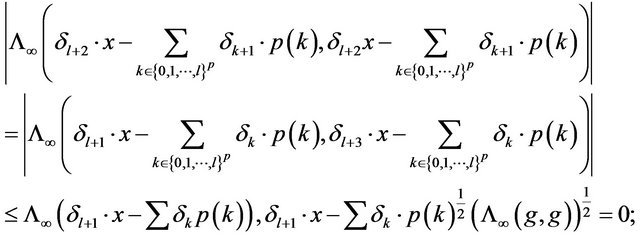
where we have denoted with
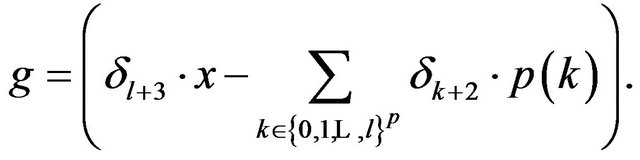
That is  is a surjective isometry, insures that
is a surjective isometry, insures that 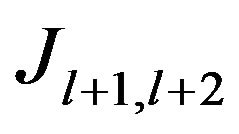 is an isomorphism of vectorial spaces. By recurrence,
is an isomorphism of vectorial spaces. By recurrence, 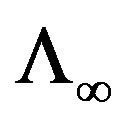 , the unique extension of
, the unique extension of 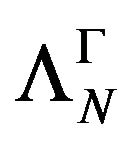 as a hspf with property b) in Remark 3.1 is stable at any
as a hspf with property b) in Remark 3.1 is stable at any 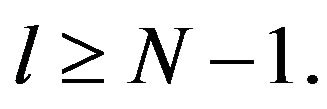
Corollary 4.8. Let  be an operator-valued kernel, positively defined and
be an operator-valued kernel, positively defined and  the hspf associated with
the hspf associated with 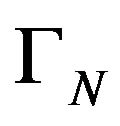 as above. If
as above. If 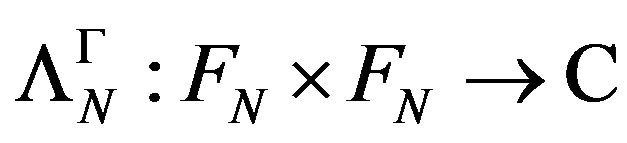 is stable at one indices
is stable at one indices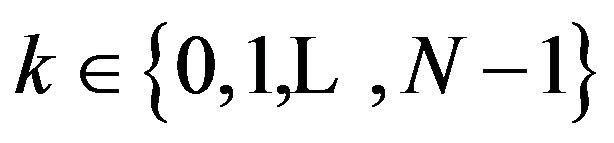 , then
, then  is stable at any
is stable at any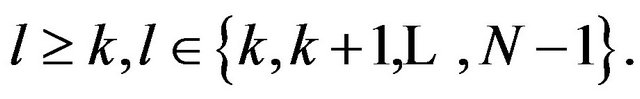
Proof. The unique extension of ,
,  as a hspf and with property b) in Remark 3.1 is the
as a hspf and with property b) in Remark 3.1 is the 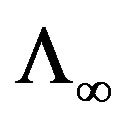 extension which is stable at any
extension which is stable at any  that is
that is 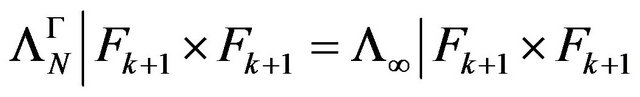 is stable at
is stable at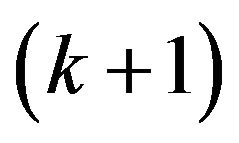 . It follows by recurrence that
. It follows by recurrence that 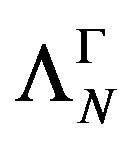 is stable at any
is stable at any 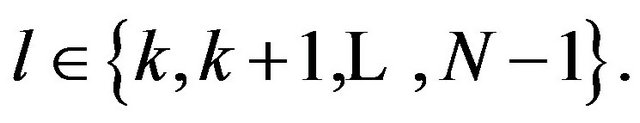
In the sequel, we argue like in [1], Remark 2.9.
Remark 4.9. Let 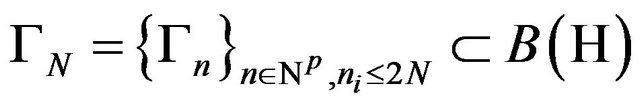 be an operator kernel, positively defined,
be an operator kernel, positively defined, 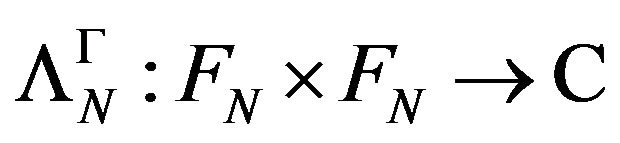 the hspf associated with the kernel
the hspf associated with the kernel 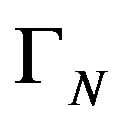 as previous, stable at
as previous, stable at  and
and , the unique extension of
, the unique extension of 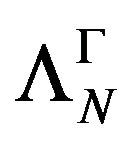 to
to  as hspf and with property b) in Remark 3.1, defined in Proposition 4.5. Let
as hspf and with property b) in Remark 3.1, defined in Proposition 4.5. Let 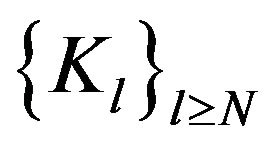 be the Hilbert spaces constructed via
be the Hilbert spaces constructed via  because
because  is stable at any
is stable at any 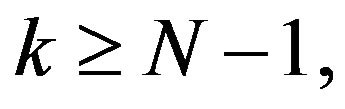 the isometries
the isometries ,
,  ,
,  are bijective one, that is
are bijective one, that is 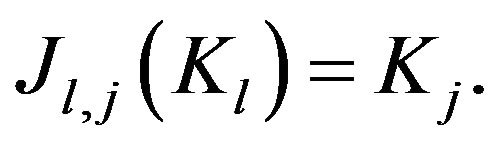 We denote with
We denote with 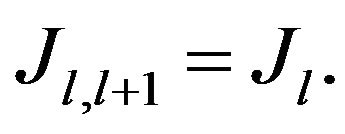 We may construct the p-tuple of commuting selfadjoint operators
We may construct the p-tuple of commuting selfadjoint operators 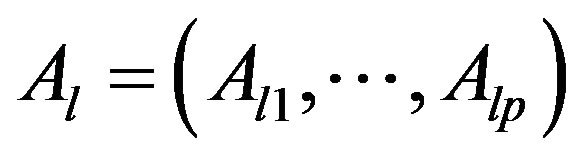 on the space
on the space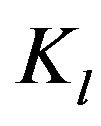 ,
, 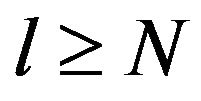 , as in Proposition 4.2. We define as in Remark 4.1 (A) the operators
, as in Proposition 4.2. We define as in Remark 4.1 (A) the operators 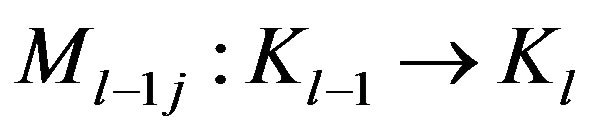 by
by
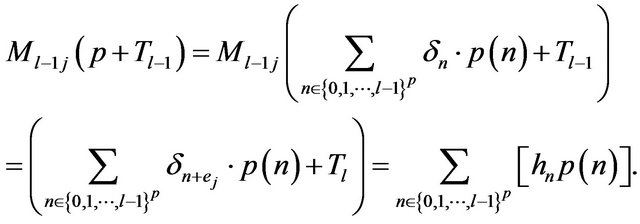
We have immediately:
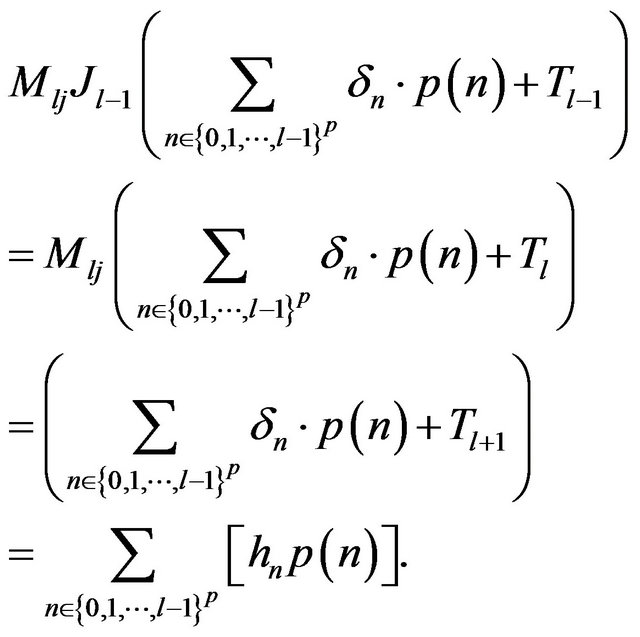
modulo  for all
for all 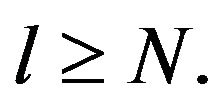 It results
It results 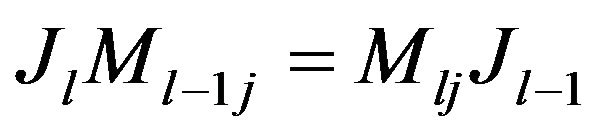 that imply
that imply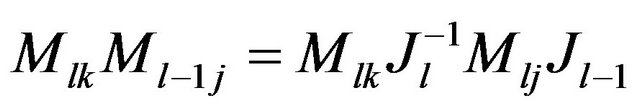 ; respectively
; respectively
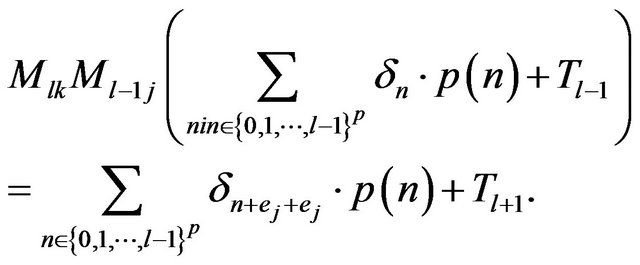
Consequently
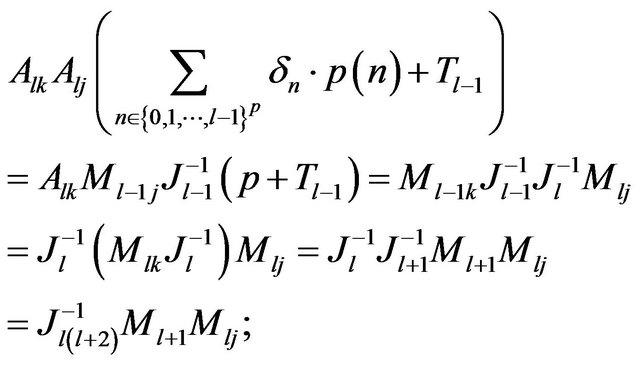
consequently we obtain:
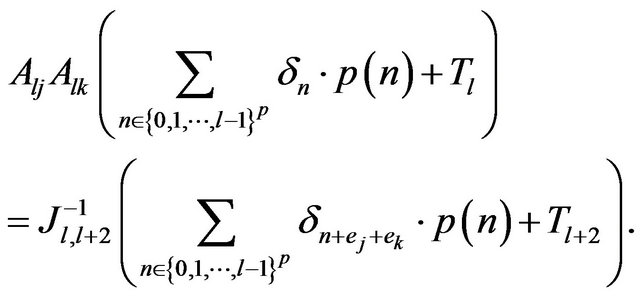
A recurrence argument leads to the formula:
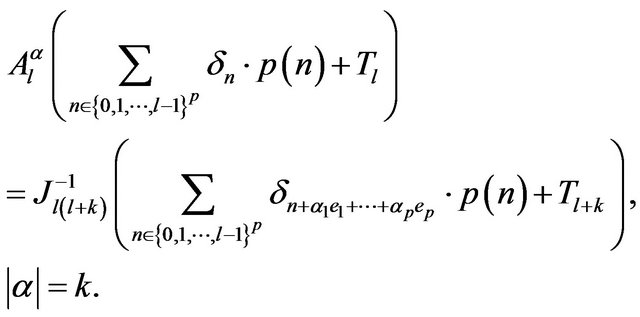
Let
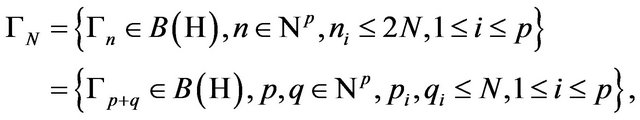
subject on the same conditions as in Remark 4.2. We denote with 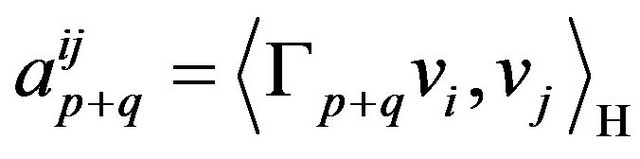 with
with 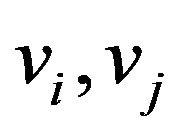 C-linear vectors in a basis of H,
C-linear vectors in a basis of H, .
.
Proposition 4.10. Let 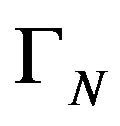 be an operator kernel, stable at
be an operator kernel, stable at , as above. We consider that:
, as above. We consider that:
1) for all , we have
, we have  , with
, with  vectors in a basis of
vectors in a basis of , and
, and 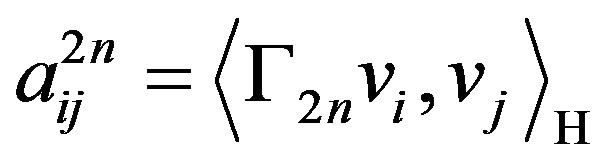 for all
for all ,
, . In this case, for all
. In this case, for all  the elements
the elements 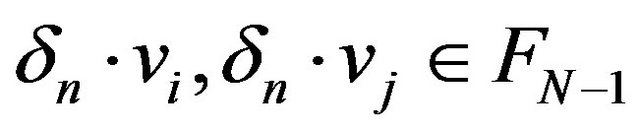 are linear independent in
are linear independent in 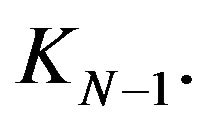
2) Moreover, we consider in addition, that the kernel  is such that for all
is such that for all , as in 1),
, as in 1), 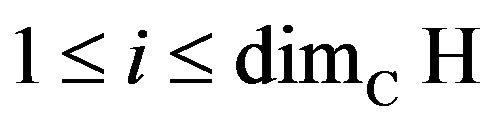 the elements
the elements
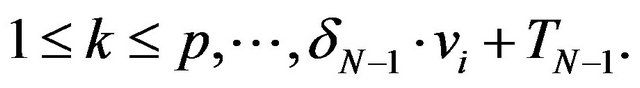
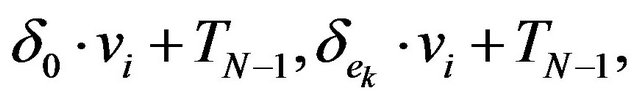
are C-linear independent in 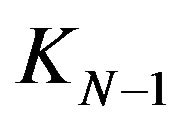 and for any
and for any ,
,  , and any
, and any  the elements
the elements
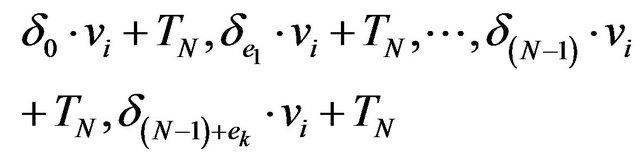
are linear dependent in KN (in 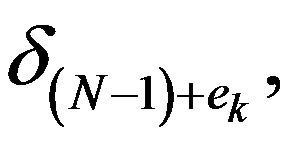
 stands for
stands for ).
).
Proof. 1) Indeed, let us show, that, if we have 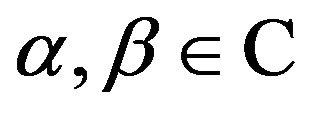 such that (14)
such that (14)
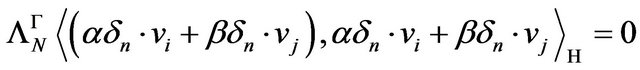
it results  We have
We have
 (14)
(14)
Immediately, from above, we have:
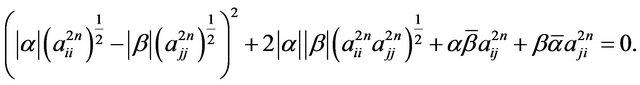 (15)
(15)
In the same time, from Cauchy-Buniakowski-Schwarz inequality, we have:
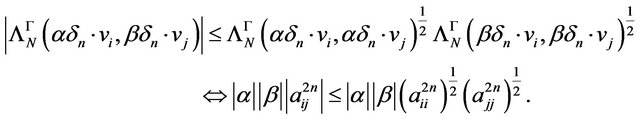 (16)
(16)
Equatities (15) can be satisfied, in case of (16), only when
 (17)
(17)
are true. In condition of Proposition 4.10. 1), the only case in which (17) can happen is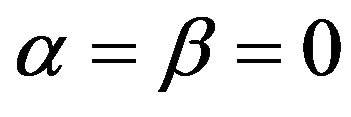 ; that is
; that is  are linear independent elements in
are linear independent elements in 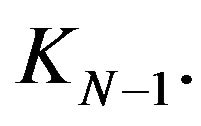
Theorem 4.11. Let  be an operator kernel, positively defined, stable at
be an operator kernel, positively defined, stable at , such that its terms
, such that its terms  satisfy conditions 1) and 2) in Proposition 4.10, that is: for all
satisfy conditions 1) and 2) in Proposition 4.10, that is: for all , there exists {
, there exists {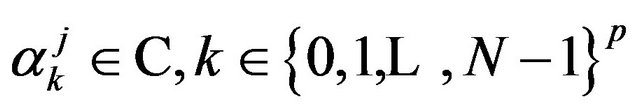 with at least one
with at least one 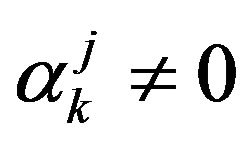 } such that
} such that
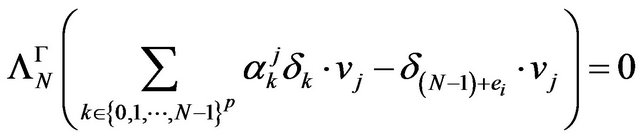
with  the hspf associated with the kernel
the hspf associated with the kernel  as previous. Then, there exists a d-atomic positive operator-valued representing measure
as previous. Then, there exists a d-atomic positive operator-valued representing measure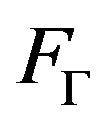 , with
, with  atoms, on a compact set in
atoms, on a compact set in 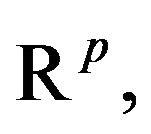 such that:
such that:
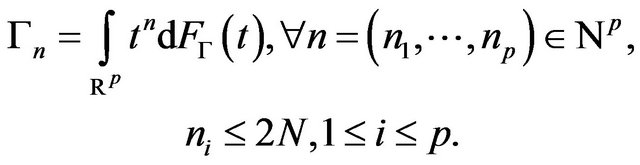
Proof. As in Proposition 4.3, in the same conditions about the kernel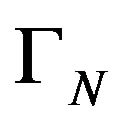 , stable at
, stable at 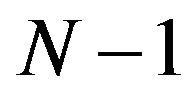 and with the same notations, we obtain a commuting p-tuple of selfadjoint operators
and with the same notations, we obtain a commuting p-tuple of selfadjoint operators ,
, 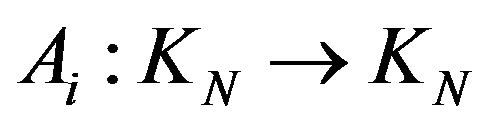 ,
,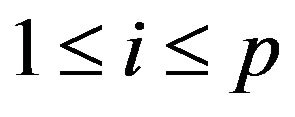 . From [7], when we aplly Kolmogorov’s decomposition theorem to the positive definite kernel
. From [7], when we aplly Kolmogorov’s decomposition theorem to the positive definite kernel , we get the representations:
, we get the representations: 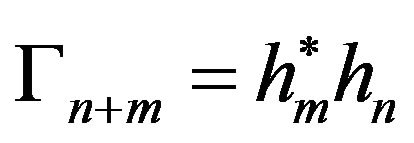 for every
for every  with the operators
with the operators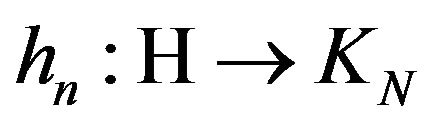 ,
,
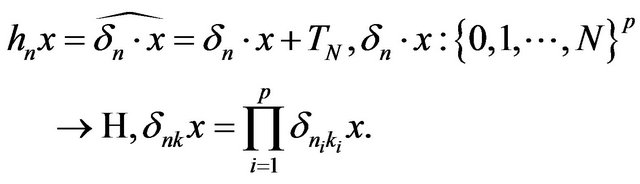
Accordingly to Remark 4.4, we have: 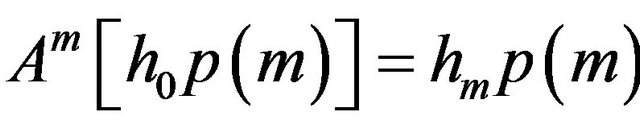 for every
for every  and every arbitrary vector-value
and every arbitrary vector-value . That is the representations
. That is the representations 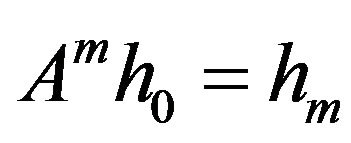 occur, and by replacing in the above representations, we obtain
occur, and by replacing in the above representations, we obtain
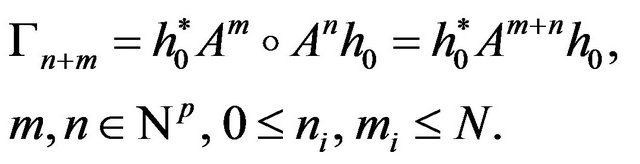
In these conditions, with respect to the joint spectral measure associated to the commuting tuple A, acting on the finite dimensional Hilbert space , the join spectrum
, the join spectrum  with
with  the spectrum of the bounded operator
the spectrum of the bounded operator  defined on
defined on . The set consists only of isolated, in finite number, principal values of
. The set consists only of isolated, in finite number, principal values of ; consequently
; consequently  is an atomic set and the joint spectral measure
is an atomic set and the joint spectral measure  of A is an atomic one. With respect to the joint spectral measure, we have
of A is an atomic one. With respect to the joint spectral measure, we have
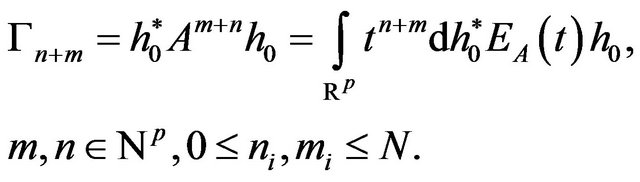
We denote with  for any
for any  a positive, operator-valued atomic measure and obtained the representations:
a positive, operator-valued atomic measure and obtained the representations:
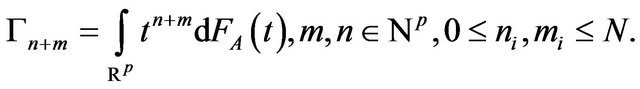
We consider the vector space
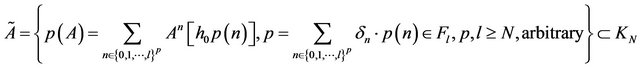
and define the map  when
when
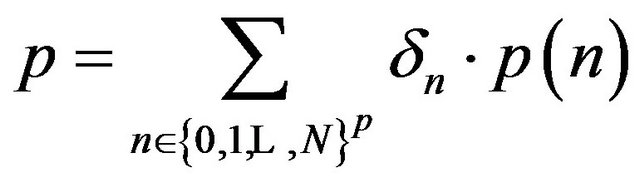
and
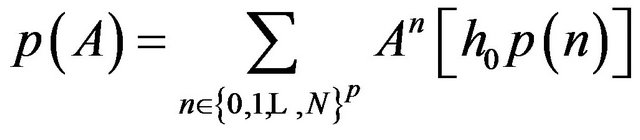
To check the definition is correct, we shall use again Remark 4.4 and show that, if , with
, with , we have
, we have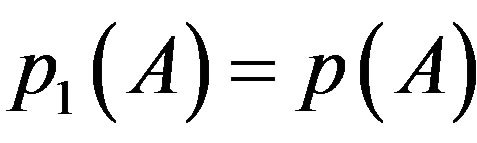 . Indeed,
. Indeed, 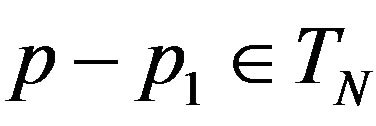 means that
means that
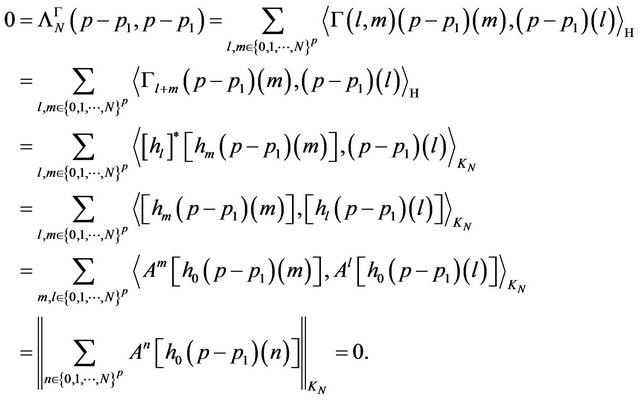
That is  From the definition,
From the definition,  is linear; we prove that
is linear; we prove that  is also injective. Let us consider
is also injective. Let us consider
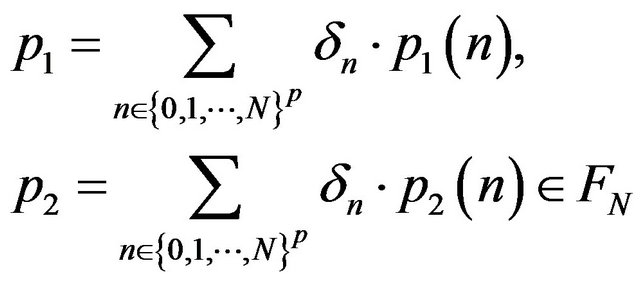
such that  that is:
that is:
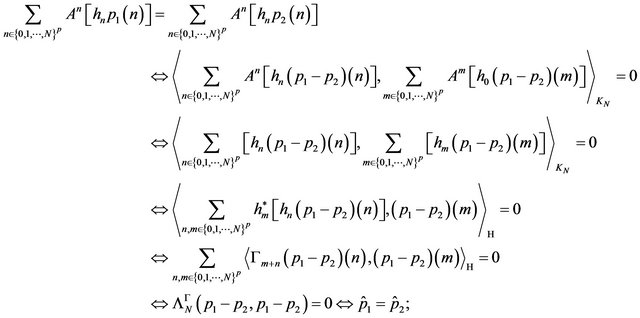
that is  is an injective map. We show that
is an injective map. We show that
 is also a surjective map. We consider the element
is also a surjective map. We consider the element  and prove that there exists
and prove that there exists  such that
such that 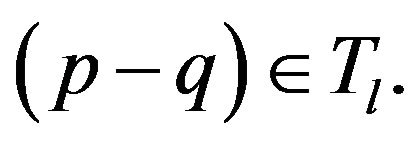 Indeed,
Indeed,  is stable at any
is stable at any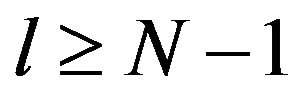 , by recurrence, in Proposition 4.7, we have proved that there exists
, by recurrence, in Proposition 4.7, we have proved that there exists  such that
such that  that is
that is
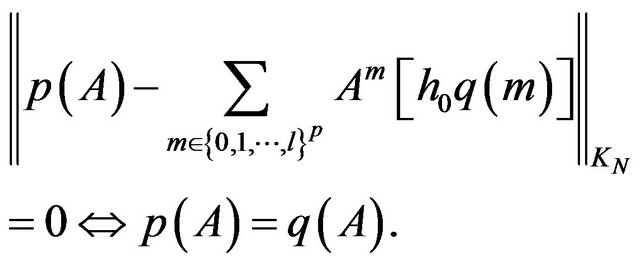
The map , above defined, is an isomorphism of vectorial spaces, consequently:
, above defined, is an isomorphism of vectorial spaces, consequently: 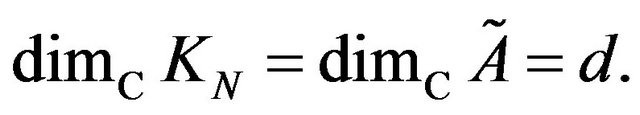
Let also
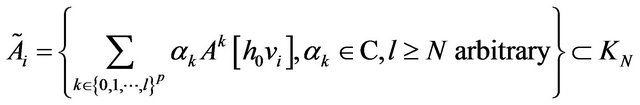 with
with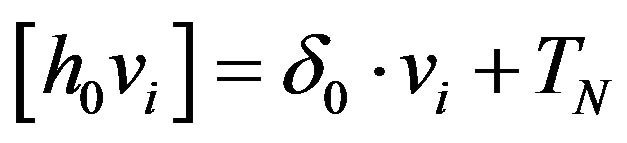 . Obviously,
. Obviously, 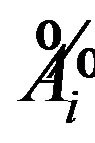 is a subspace in
is a subspace in 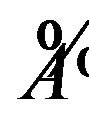 (the subspace generated in
(the subspace generated in 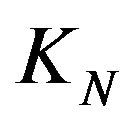 by
by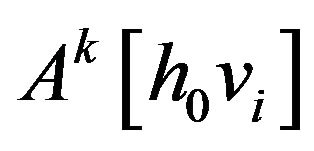 ). Because of property 2) Proposition 4.10. of the kernel
). Because of property 2) Proposition 4.10. of the kernel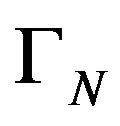 , there exists scalars
, there exists scalars 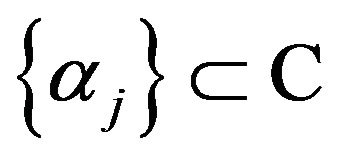 such that
such that
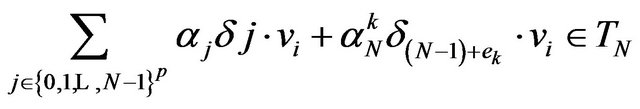 ;
;
that is
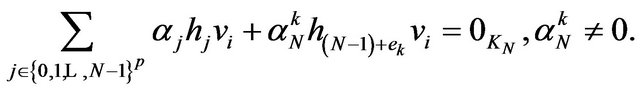
It follows that
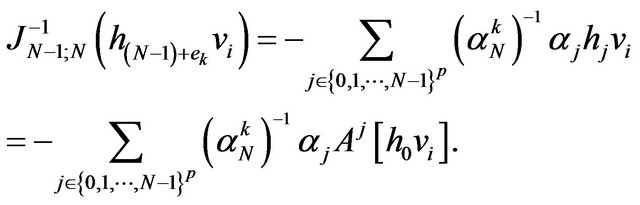
Because  is an isomorphism of vectorial spaces, the obtained representation is uniquely determinated (modulo TN) and it results easily from Remark 4.4). From property 1) of the kernel
is an isomorphism of vectorial spaces, the obtained representation is uniquely determinated (modulo TN) and it results easily from Remark 4.4). From property 1) of the kernel , we have
, we have  whenever
whenever , and also from 2),
, and also from 2), 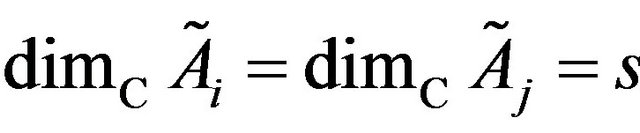 for all
for all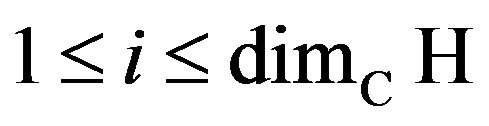 . We have proved in this way that
. We have proved in this way that  (
( represents the direct sum.) With the usual operator’s multiplication
represents the direct sum.) With the usual operator’s multiplication 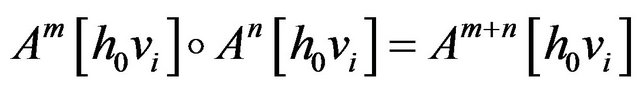 for all
for all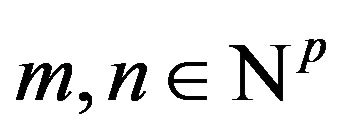 , and from Remark 4.9, endowed with an echivalent norm induced on
, and from Remark 4.9, endowed with an echivalent norm induced on  by the norm on
by the norm on 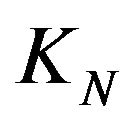 via the map
via the map , the subspaces
, the subspaces 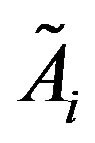 have all a structure of unital commuting C* algebra with dimension
have all a structure of unital commuting C* algebra with dimension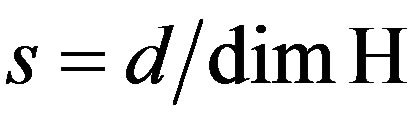 , and
, and . In these conditions, the joint spectral measure of
. In these conditions, the joint spectral measure of
 has precisely s characters, therefore, the joint spectrum
has precisely s characters, therefore, the joint spectrum  has exactely s atoms. Because of the representation
has exactely s atoms. Because of the representation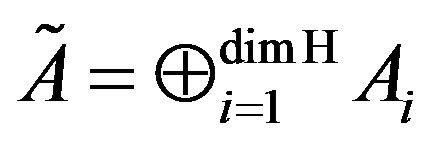 , it follows that the joint spectrum of A has exactely
, it follows that the joint spectrum of A has exactely 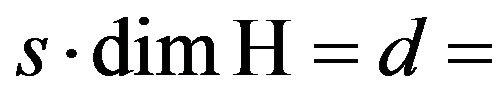
 atoms. Consequently the measure
atoms. Consequently the measure , in
, in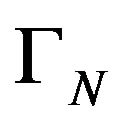 ’s representations, has the same number
’s representations, has the same number  of atoms.
of atoms. 
5. Conclusion
We adapt the concept of “stability of the dimension”, in [1], of some Hilbert spaces obtained as the qotient spaces of scalar polynomials of finite degree with respect to the null space of the Riesz functional, to that of “stability of the dimension” of some Hilbert spaces obtained as the quotient spaces of some vectorial-valued functions with respect to the null space of some hermitian square positive functional associated with a positive defined kernel of operators. The stability of this dimension is considered in connection with a truncated operator valued moment problem. The stability of the dimension of the obtained Hilbert space, represents the conditrion for stability of the number of atoms of the obtained operator-valued atomic representing measure for the given kernel.