Modeling Natural Gas Productivity Recovery from a Hydrate Reservoir Well ()
1. Introduction
Gas hydrates are crystalline inclusion compounds in which gas molecules are held as guests in a metastable host lattice made up of water molecules. The gas hydrates are formed when gas and water mixtures are subjected to high pressure or low temperature conditions [1]. These conditions are found in subsurface environments of deep-sea sediments and permafrost regions, where the presence of in situ hydrates has been confirmed by extensive exploration activities around the world [2]. One volume of hydrate could release 150 to 180 volume of natural gas at standard conditions [3]. The high concentration of natural gas puts the energy content of hydratebearing formations on par with bitumen and heavy-oil reservoirs, and much higher than the energy content of other unconventional sources of gas, such as coal bed methane and tight gas [4]. World reserves of natural gas hydrate have been estimated to be the largest fossil fuel resource among the known reserves of conventional natural gas and oil [5]. Thus, developing methods for commercial production of natural gas from hydrates has enormous economical and strategic importance [6,7].
Naturally occurring hydrate formations are present as a solid in the hydrate-stability zone. Hydrate will remain a solid until formations are moved outside of the hydratestability region. The hydrate-stability region is a function of pressure, temperature and composition of the gas and fluid in the pore space [8]. The hydrate dissociates when its temperature increases to above the temperature of hydrate formation at a specified pressure, or when the system pressure decrease to below the pressure of hydrate formation at a specified temperature rapture. When a well is drilled in to a hydrate reservoir, it initiates a depressurization that leads to decomposition of hydrate and release of hydrate gas.
The demand of natural gas as a clean source of energy is rapidly increasing in the world. Natural gas hydrates are drawing attention worldwide as an unconventional source of energy because of the vast availability of this resource of energy and the foreseen increase in the demand of natural gas. The estimates on the amount of natural gas being trapped within gas hydrate deposits vary within the limits of 1015 to 1019 standard m3. It has been assessed that the current world energy consumption could be sustained for 180 years only by recovering one tenth of this class of trapped gas [8,9].
In order to produce gas from hydrate reservoir, it is necessary to destroy the crystalline water structure which traps the hydrocarbons. From a technical point of view, all potential schemes of gas production from hydrate reservoirs need to achieve at least the following three objectives:
• bring the pressure and temperature around hydrate particles outside the hydrate-stability zone;
• sustain the energy required for endothermic dissociation reaction of hydrates;
• provide the means to transfer of gas from the dissociation to production wells.
According to these requirements, three possible basic gas recovery mechanisms have been suggested in Figure 1: 1) depressurization, 2) thermal stimulation, and 3) inhibitor injection.
There are a number of challenges associated with producing gas from hydrate reservoirs. The gas hydrate phase is immobile and impairs flow conditions within the reservoir. This could slow down the depressurization rate within the reservoir and consequently reduce the rate of hydrate dissociation. Another issue is that the sensible energy within the reservoir may not be enough to provoke hydrate dissociation at an economical rate. The temperature drop due to dissociation process could slow down the dissociation rate. Additionally, after dissociation, released free water may freeze and end up as ice which obstructs the flow in porous media (even without freezing, the free water impairs gas production).
The goal of Holder [9] study was to estimate the contribution of gas-hydrates to the total gas production of the reservoir. This study examines the dissociation of methane hydrates in a square reservoir of uniform thickness. The three-dimensional [10], two-phase (gas/water) reservoir simulation model of this study was developed to address fundamental questions regarding the feasibility of production schemes for gas reservoirs which were in contact with a gas-hydrate cap. The production of gas results in gas depressurization at the hydrate-gas interface. A one-dimensional, three-phase flow model was developed in this study to simulate the process of gas production from Berea sandstone samples containing methane hydrate by means of a depressurization mechanism [11]. A one-dimensional linearized model suggested by Makogon [5] was used in the analysis [12]. The temperature and pressure distributions in porous layer of methane hydrate and in the gas region were evaluated for different well pressures and reservoir temperatures. A 2D cylindrical simulator for gas hydrate reservoirs was developed by Hong [13]. The model includes the equations for two phase (gas-water) flow, conductive and convective heat transfer, and intrinsic kinetics of hydrate decomposition. The developed simulator was used to study a hydrate reservoir where the hydrate-bearing layer overlies a free-gas zone.
The complete numerical modeling of this type of reservoir is still at its developing stages. The reservoir modeling of this type of reservoir is still not clear because its dynamics and the role of parameters that control these dynamics have not been fully understood. Therefore, the need of the development as a tool that can further our understanding of the complication of this type of reservoirs and provide guidance for their exploitation is considered almost critical.
This work is undertaken to develop a model to predict the performance of a naturally occurring in situ hydrate reservoir. The kinetics model is incorporated in to the radical diffusivity equation using a gas mass balance in gas hydrate reservoirs well, then, the model is solved analytically. The proposed model is used to describe the gas potential of an example reservoir and to compare gas production estimates with data from other published studies.
2. Modeling Gas Production from Methane Hydrate
This section provides a detailed methodology used to model gas production. A kinetics model is developed and hydrate decomposition model to describe gas production from the gas hydrate well.
Methane hydrate, which makes up most of naturally
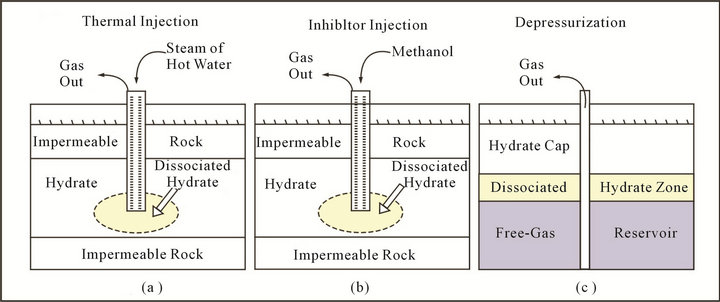
Figure 1. Schematic of gas recovery from gas hydrate methods.
occurring hydrates, is composed of roughly six molecules of water for each molecule of methane. Therefore, natural gas production from dissociation of methane hydrate in an unbounded axis symmetric reservoir due to drilling of a depressurization well is studies. The reaction of methane with water to form hydrate is represented by

Under thermodynamically favorable conditions, the water molecules form a cage around the methane molecule and from the solid hydrates. When the pressure decrease or the temperature rises, the reaction reverses and the hydrate decompose into CH4 and water.
3. Methodology to Model the Productivity
The hydrate reservoir is represented by a cylindrical geometry of the hydrate reservoir is represented as shown in Figure 2. As hydrates dissociate into gas, two regions are formed in the reservoir, one containing dissociated gas and other undissociated hydrates. These two regions are separated by an interface, located at r, which moves as the hydrates dissociate, and the r0 is the borehole radius, R is the effective radius of gas hydrate reservoir. When r = R, the reservoir will no gas recovery again.
The hydrate dissociation results in gas release from the reservoir. If nL represents the moles of gas released from the at time t. Thus the molar rate of gas released from the reservoir is given by . This rate is proportional to the hydrate decomposition rate as the moles of gas produced from a hydrate reservoir depend on the amount of hydrate dissociated.
. This rate is proportional to the hydrate decomposition rate as the moles of gas produced from a hydrate reservoir depend on the amount of hydrate dissociated.
The hydrate dissociates by the destruction of hydrate
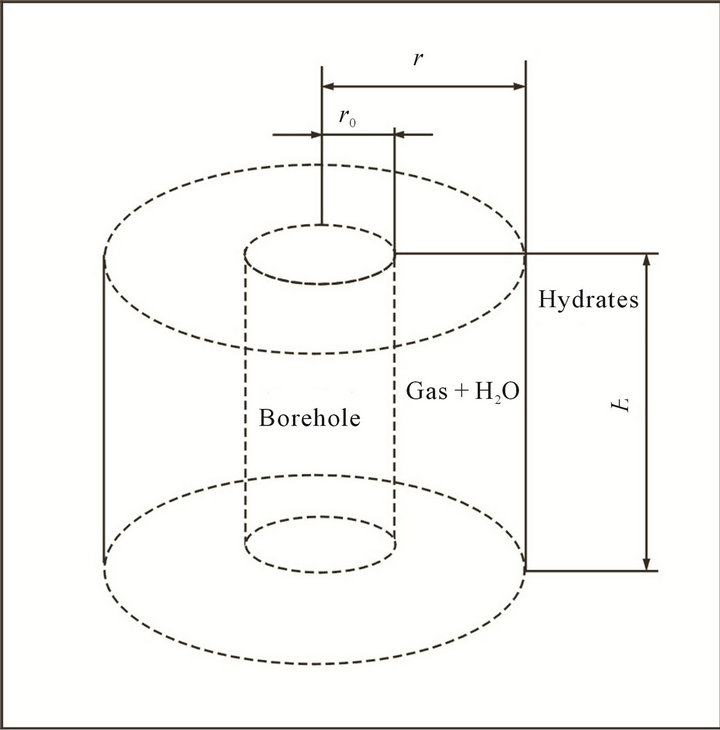
Figure 2. Reservoir schematic for kinetics model.
lattice and the release of gas from its interstices. The lattice destruction depends on a driving force applied across it; in case of depressurization induced dissociation, this driving force is the differential pressure across the hydrate lattice. As the differential pressure is applied to the hydrate surface, the hydrate lattice near the surface breaks down first, thereby releasing gas from the surface itself. For the same differential pressure, the hydrate dissociation will be greater for a larger surface area of the hydrate lattice exposed to the driving force. Hence, the hydrate dissociation rate depends on the surface area of the dissociating hydrate and on the pressure differential across the hydrate surface. The differential pressure is the difference between the pressure at hydrate-gas phase equilibrium Peq and the pressure for dissociation PD. Therefore, the molar rate of gas released from a hydrate reservoir is proportional to the hydrate surface area As and to the differential pressure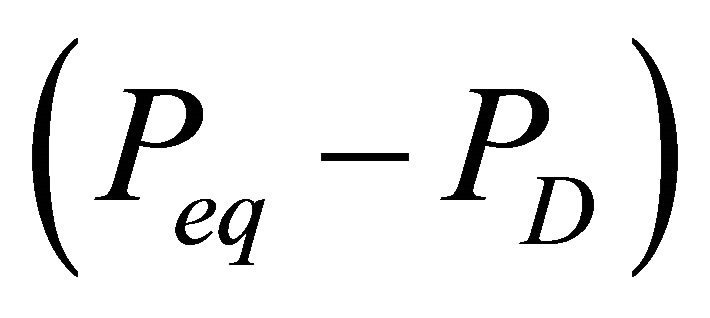 .
.
The equilibrium pressure Peq is a function of the reservoir temperature. When the hydrates dissociates in the reservoir, the reservoir temperature near the dissociating surface will decrease. This decrease in temperature will cause a decrease in the equilibrium pressure Peq, and thus, a decrease in the driving force for further dissociation of the hydrates. Therefore, the gas release rate will decrease as the hydrate dissociation progresses. This temperature effect on the dissociation rate can be approximated by describing the driving force 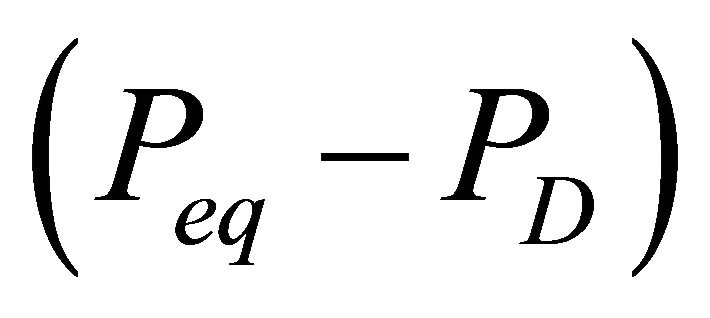 as an nth order differential pressure
as an nth order differential pressure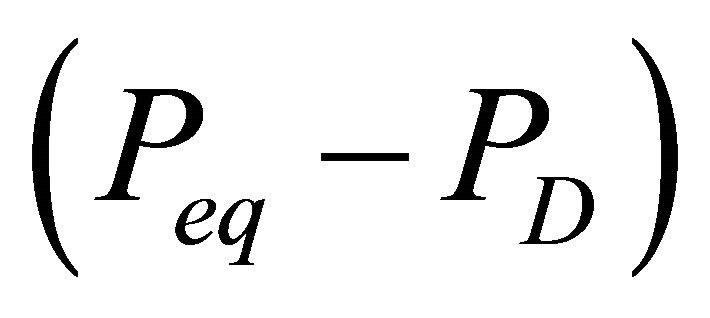 , where n is kinetics model order, the driving force is less
, where n is kinetics model order, the driving force is less  for n values less than 1. With this simplification, the hydrate decomposition can be defined by an nth order driving forceinduced decomposition kinetics model where the molar rate of gas released from the hydrate reservoir is given by
for n values less than 1. With this simplification, the hydrate decomposition can be defined by an nth order driving forceinduced decomposition kinetics model where the molar rate of gas released from the hydrate reservoir is given by
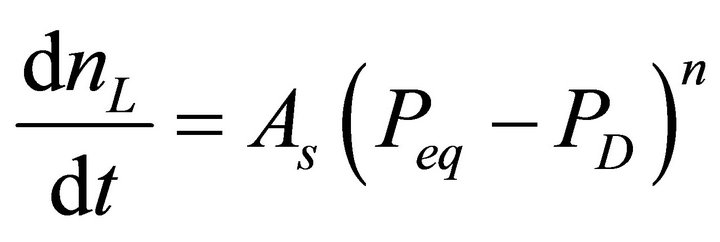 . (1)
. (1)
The kinetics model described by Equation (1) can be simplified by using gas mass balance and an appropriate equation of state. For a hydrate volume of
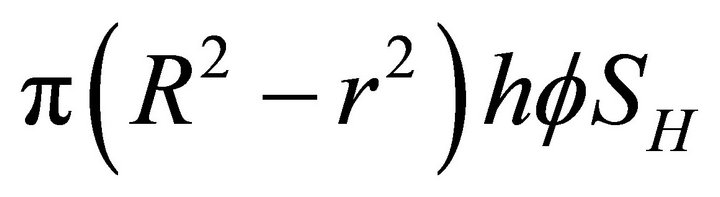 [1], the initial moles of gas trapped in the reservoir is by Equation (1)
[1], the initial moles of gas trapped in the reservoir is by Equation (1)
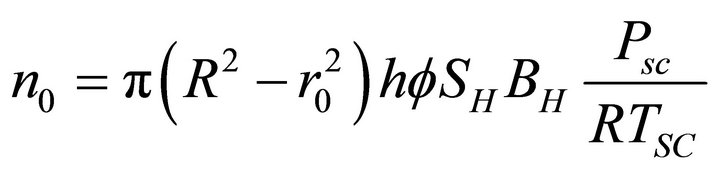 (2)
(2)
where,  is porosity (30%), h is reservoir thickness, SH is hydrate saturation (20%) and BH is the gas hydrate formation factor and is defined as the ratio of a standard volume of gas trapped in a unit reservoir volume of the hydrate. The value of BH is from 160 to
is porosity (30%), h is reservoir thickness, SH is hydrate saturation (20%) and BH is the gas hydrate formation factor and is defined as the ratio of a standard volume of gas trapped in a unit reservoir volume of the hydrate. The value of BH is from 160 to , as a cubic meter of the hydrate is known to contain about from 160 to 181 SCM of methane gas.
, as a cubic meter of the hydrate is known to contain about from 160 to 181 SCM of methane gas.
Therefore, in the unit’s time, the gas recovery from reservoir is given by Equation (3)
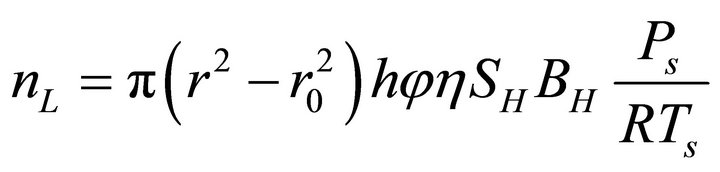 (3)
(3)
As the hydrates dissociate up to a distance RD, the hydrate volume remaining in the reservoir is
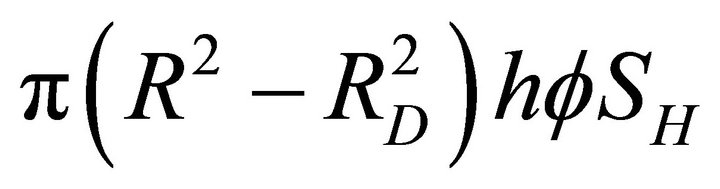 . This volume contains nH moles of methane gas as
. This volume contains nH moles of methane gas as
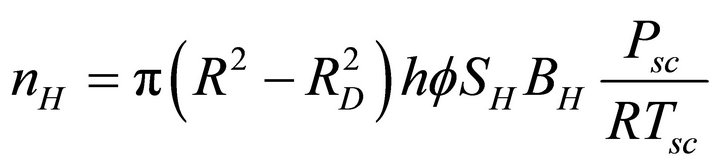 (4)
(4)
Rearranging Equation (3), an expression for RD is obtained as
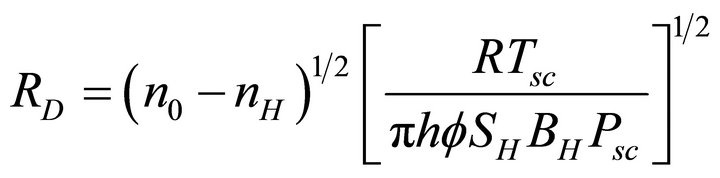 (5)
(5)
This interface is assumed to be the surface where the hydrates dissociate, so the hydrate dissociation surface area, As, is the surface area of the cylindrical hydrates dissociate up to a distance R. Thus
 (6)
(6)
Substituting Equation (3) into Equation (6), the molar rate of gas production becomes, c1 and c2 are constant of integration.
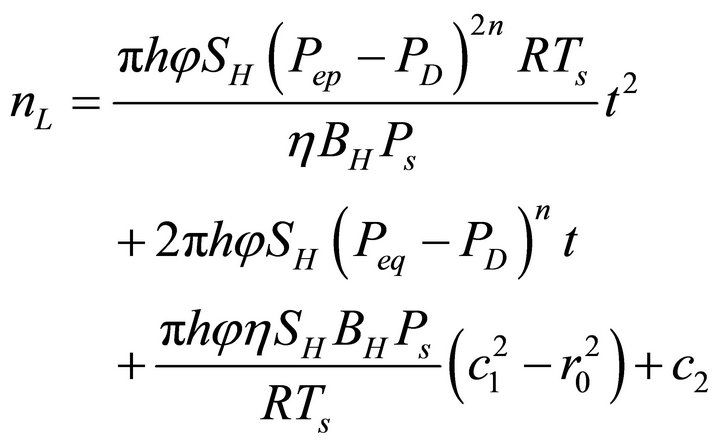 (7)
(7)
4. Conclusions
It is expected that before commercial gas production from hydrates becomes reality, technology advancements in geophysical and geological methods must lead to improved macroscopic characterization of hydrate reservoirs. Gas production from hydrate dissociation being a new area of research, the important of all these unknowns on the quality of predictions is not fully known because the study of the subject is far from complete, and its complexity is compounded by the case-specificity of the dissociation methods.
A new model is developed to predict the performance of an in situ gas hydrates. The model couples nth order decomposition kinetics with gas flow through porous media. The models provide a simple and useful tool for hydrate reservoir analysis without using any empirical correlation. The model shows that the hydrate decomposition is very slow with a pressure drive mechanism, and this low rate may be increased by using chemical enhancers.
5. Acknowledgements
This study was sponsored by the National Natural Science Foundation of China (41174159).
NOTES