1. Introduction
The Random Variable (RV) plays an important role in modeling many events [1,2]. In particular the sum of exponential random has important applications in the modeling in many domains such as communications and computer science [3,4], Markov process [5,6], insurance [7,8] and reliability and performance evaluation [4,5,9, 10]. Nadarajah [11], presented a review of some results on the sum of random variables.
Many processes in nature can be divided into sequential phases. If the time the process spends in each phase is independent and exponentially distributed, then the overall time is hypoexponentially distributed. The service times for input-output operations in a computer system often possess this distribution. The probability density function (pdf) and cummulative distribution function (cdf) of the hypoexponential with distinct parameters were presented by many authors [5,12,13]. Moreover, in the domain of reliability and performance evaluation of systems and software many authors used the geometric and arithmetic parameters such as [10,14,15].
In this paper we study the hypoexponential distribution in the case of n independent exponential R. V. with distinct parameters 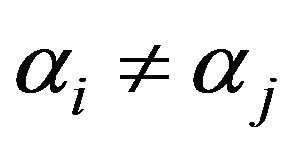 for
for 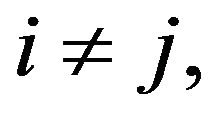 written as
written as 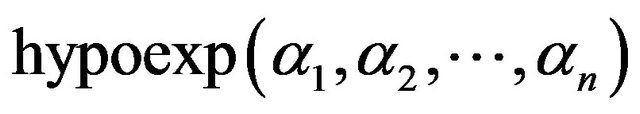 . We use in our work the properties of convolution, Laplace transform and moment generating function in finding the
. We use in our work the properties of convolution, Laplace transform and moment generating function in finding the  derivative of the pdf of this sum and the moment of this distribution of order k. In addition, we deduce some new equalities related to these parameters. Also we shall study the case when the parameters form an arithmetic and geometric sequence considered by [10,14,15] and find some new results.
derivative of the pdf of this sum and the moment of this distribution of order k. In addition, we deduce some new equalities related to these parameters. Also we shall study the case when the parameters form an arithmetic and geometric sequence considered by [10,14,15] and find some new results.
2. Definitions and Notations
Let 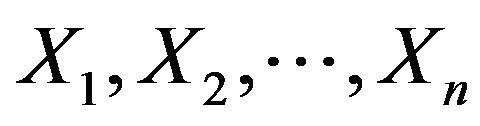 be independent exponential random variables with different respective parameters
be independent exponential random variables with different respective parameters ,
,  , written as
, written as . We define the random variable
. We define the random variable
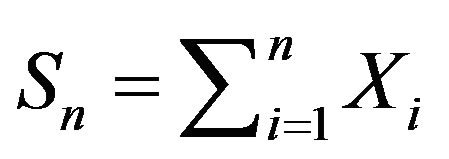
to be the Hypoexponential random variable with parameters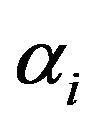 ,
,  , written as
, written as

Some notations used throughout the paper.
 :
: 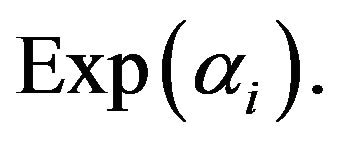
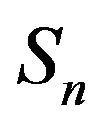 :
: 
 : The pdf of the random variable X.
: The pdf of the random variable X.
 : The cdf of the random variable X.
: The cdf of the random variable X.
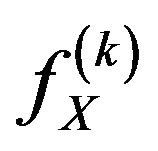 : The
: The  derivative of the pdf
derivative of the pdf .
.
 : Laplace-Stieltjes Transform.
: Laplace-Stieltjes Transform.
 : Laplace Inverse.
: Laplace Inverse.
 : The moment generating function of X.
: The moment generating function of X.
 : The moment of order k of the RV X.
: The moment of order k of the RV X.
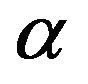 :
:  product of all parameters.
product of all parameters.
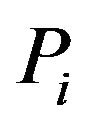 :
: 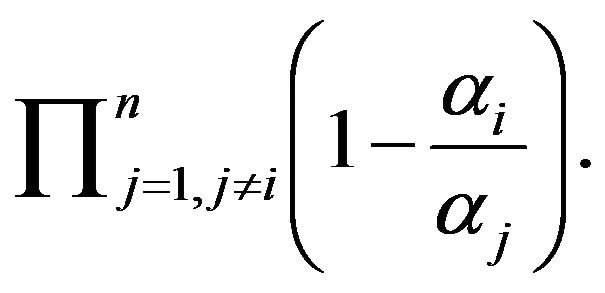
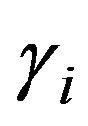 :
: 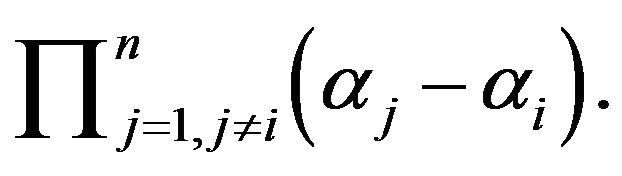
 :
: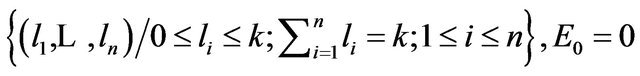 .
.
3. Applications on pdf and cdf Using Laplace Transform
The pdf and cdf of the hypoexponential with distinct parameters were presented by many authors [2,7,11-13]. We shall state in thoerem 1 and propostion 1 these results and provide another proof using Laplace transform. Next, we give some new properties of its pdf, where new identities are obtained.
Theorem 1. Let  and
and 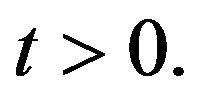 Then
Then
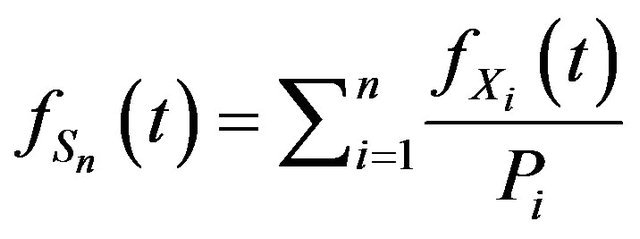
and
 .
.
Proof. We have
 where
where  for
for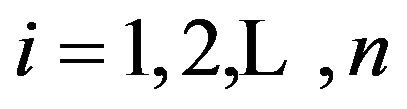 . Since
. Since  are independent then
are independent then  is the convolutions of
is the convolutions of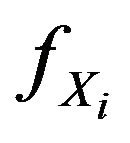 ,
,  written as
written as

and the Laplace transform of convolution of functions is the product of their Laplace transform, thus
 (1)
(1)
where  However, by Heaviside Expansion Theorem [16], for distinct poles gives that
However, by Heaviside Expansion Theorem [16], for distinct poles gives that
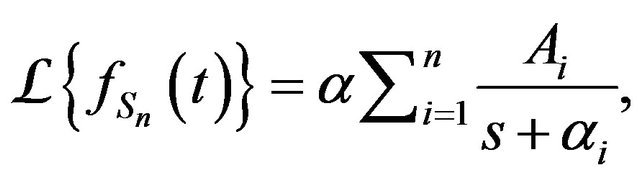
where
 .
.
Therefore,
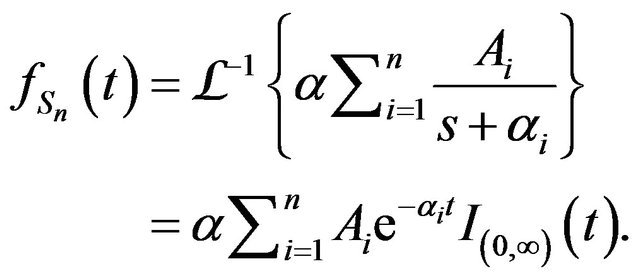
But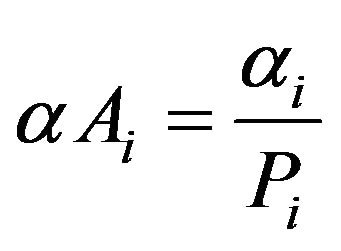 . Thus
. Thus
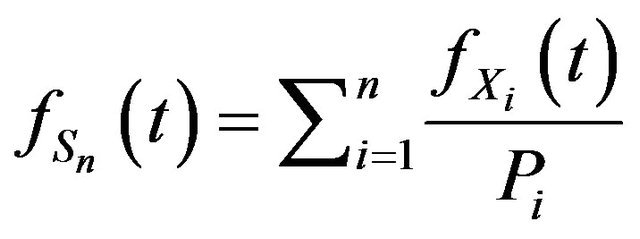 .
.
On the other hand we have
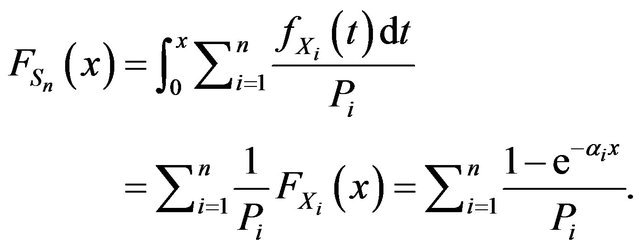
But 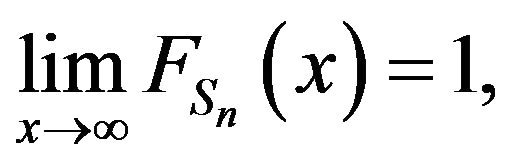 then
then  and we conclude that
and we conclude that
 .
. 
Next we shall discuss the  derivative of
derivative of  and many equalities are obtained concerning
and many equalities are obtained concerning  form and some similar forms.
form and some similar forms.
We start by noting from the previous proof that
 . Here, we shall state another simple proof using Laplace transform.
. Here, we shall state another simple proof using Laplace transform.
Proposition 1. Let . Then
. Then

Proof. We have from Equation (1),
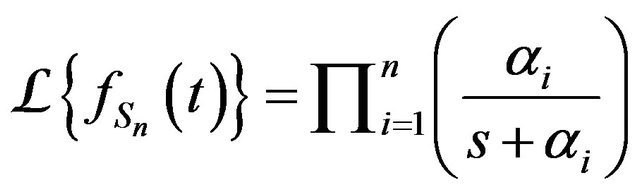
where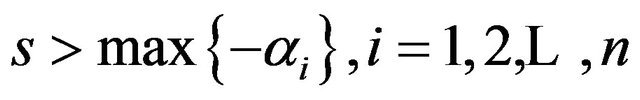 . But from Theorem 1,
. But from Theorem 1,
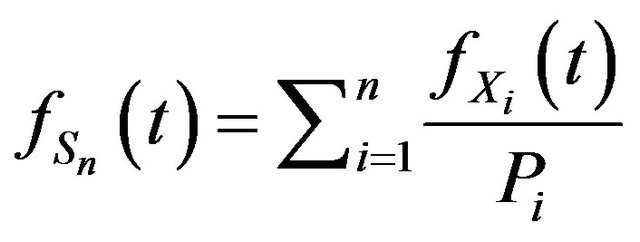
and

Hence,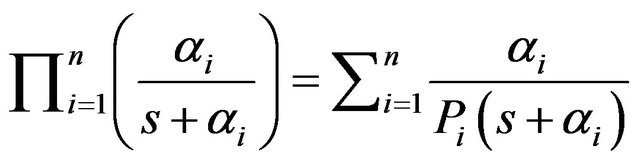 . For
. For
 Therefore,
Therefore, .
. 
Lemma 1. Let  Then
Then
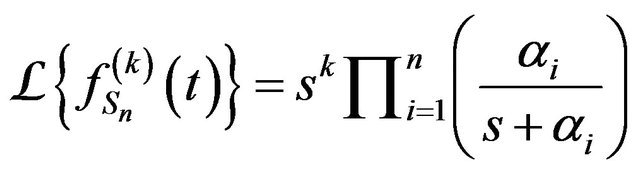
for 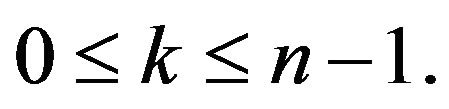
Proof. The proof is done by induction. For  we have from Equation (1)
we have from Equation (1)
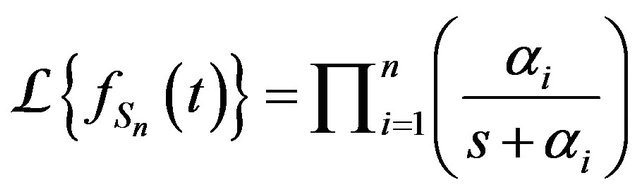 .
.
However, by Initial Value Theorem, we have

and for  we have
we have
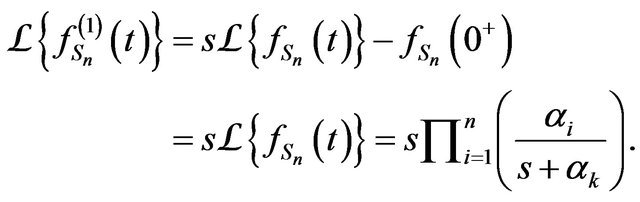
Moreover
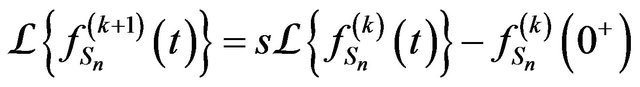
Continuing in the same manner till the  derivative, we obtain the result.
derivative, we obtain the result. 
In the following propostion we shall prove that the first  derivative of the pdf of
derivative of the pdf of  are zeros, which verifies the fact that the coefficient of variation of the hypoexponential distribution is less than one unlike the hyperexponential distribution that have the coefficient of variation greater than 1.
are zeros, which verifies the fact that the coefficient of variation of the hypoexponential distribution is less than one unlike the hyperexponential distribution that have the coefficient of variation greater than 1.
Proposition 2. Let 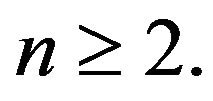 Then
Then
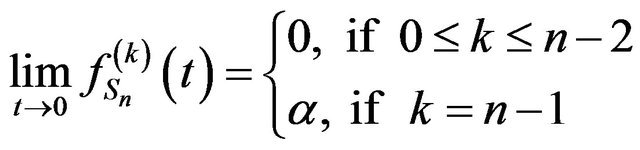
Proof. Let , we have from Lemma 1,
, we have from Lemma 1,
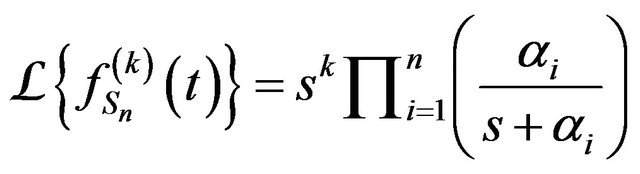
for 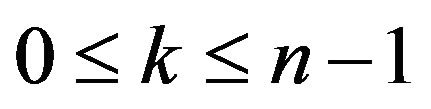 and from Initial Value Theorem, we have
and from Initial Value Theorem, we have
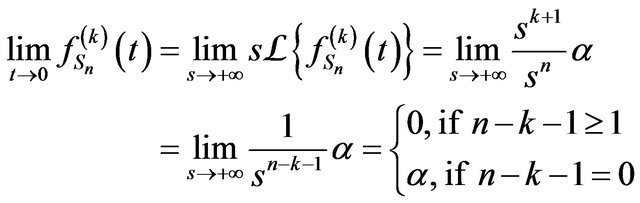

Corollary 1. Let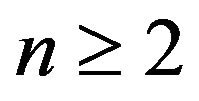 . Then
. Then
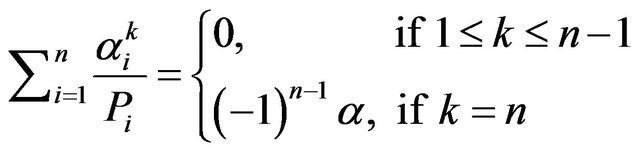
Proof. We have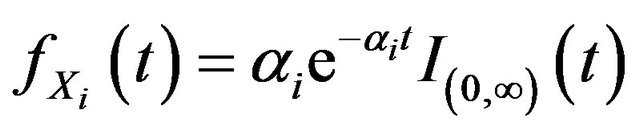 . Then the
. Then the  derivative of
derivative of 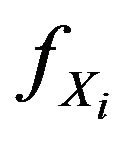 is
is
 .
.
However, from Theorem 1,
 then
then

and
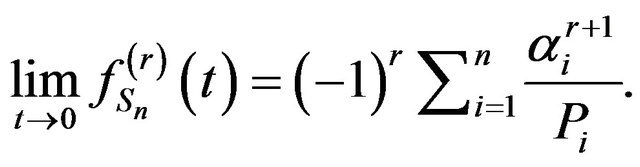 (2)
(2)
By Proposition 2, we obtain that
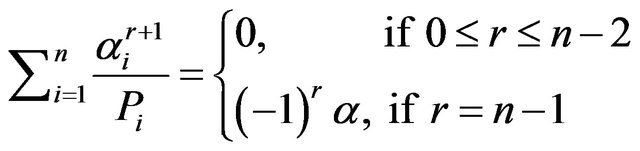
By replacing 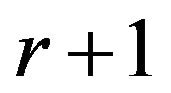 with
with 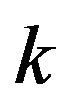 we obtain the result.
we obtain the result. 
4. Applications on pdf and cdf Using Moment Generating Function
In the previous section we saw the use of Laplace properties in the proofs of the theorems and propositions. In a similar manner, in this section we use the moment genrating function to obtain more new related results. A new form of the moment generating function of 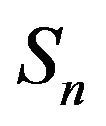 and the moment of
and the moment of 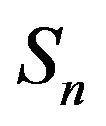 of order k is given. Moreover, we deduce more new related equalities concerning
of order k is given. Moreover, we deduce more new related equalities concerning 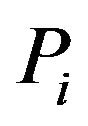 and higher order derivatives of pdf of
and higher order derivatives of pdf of .
.
Proposition 3. Let 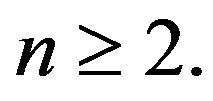 Then
Then
 .
.
Proof. We have
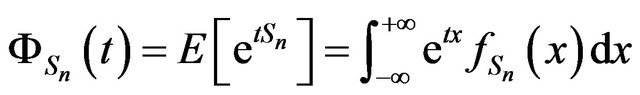
and from Theorem 1,
 then
then
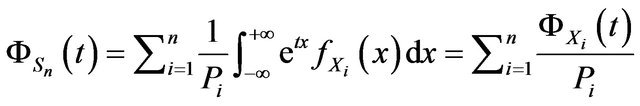 .
. 
Proposition 4. Let  and
and . Then
. Then
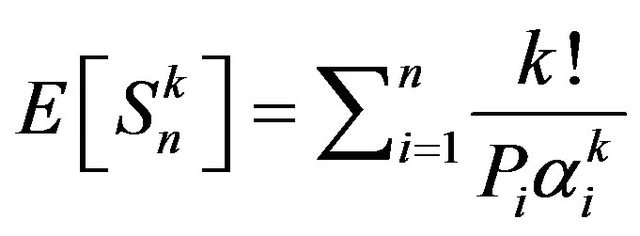
Proof. We have from Proposition 3,
 .
.
Then

and
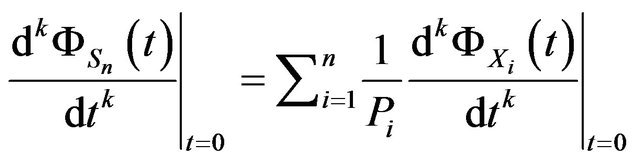
which gives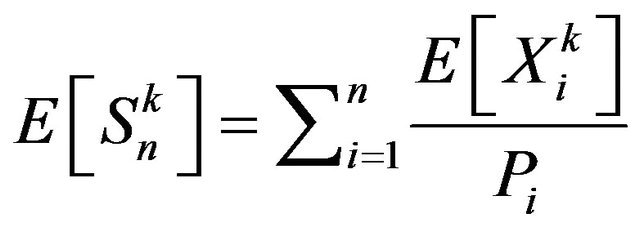 . But
. But . Thus we obtain the result.
. Thus we obtain the result. 
Next, we shall use the Proposition 3 and 4 to find other identities on 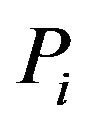 and higher orders for
and higher orders for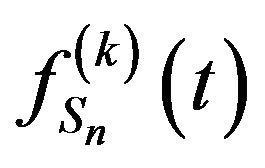 . We start by noting that
. We start by noting that  and by taking
and by taking  in Proposition 3, we again obtain the result in Proposition 1that is
in Proposition 3, we again obtain the result in Proposition 1that is .
.
Proposition 5. Let  and
and . Then
. Then
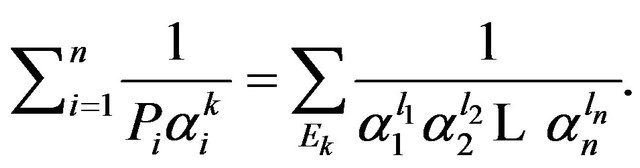
where
 .
.
Note that we may write
 , (3)
, (3)
where
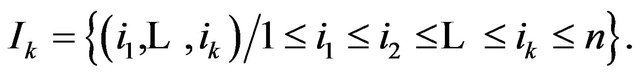
However  and
and  are equivalent representing a set of combination with repetition having
are equivalent representing a set of combination with repetition having 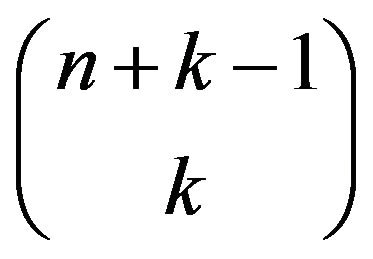
possibilities and , thus the above summation (3) shall be 1.
, thus the above summation (3) shall be 1.
Proof. Let  and
and . We have
. We have
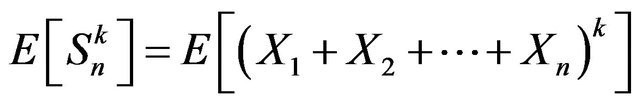
and using multinomial expansion formula, we obtain
 .
.
Knowing that expectation is linear and ,
,  are independent with
are independent with
 then
then
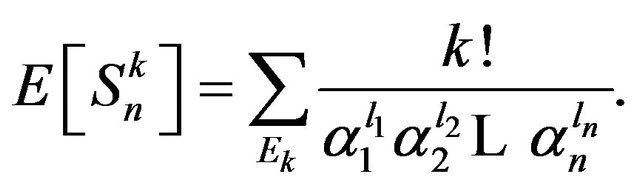 (4)
(4)
Since from Proposition 4,
 .
.
Therefore,
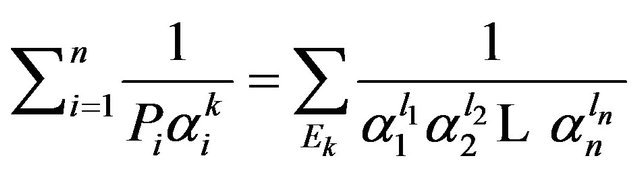 .
. 
The following corollary is direct consequence of Proposition 5 and Equation (4), taking 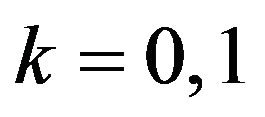 and 2 respectively.
and 2 respectively.
Corollary 2. Let . Then 1)
. Then 1) 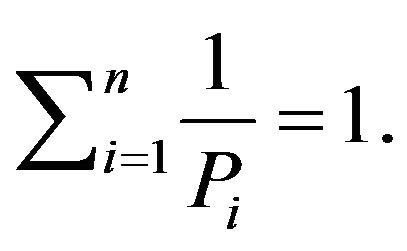
2)  and
and 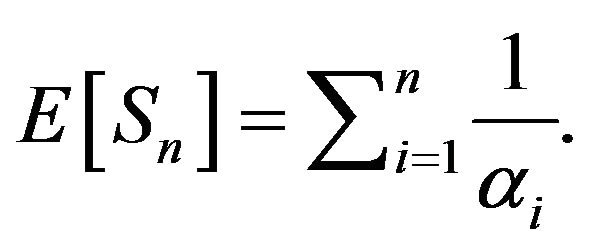
3) 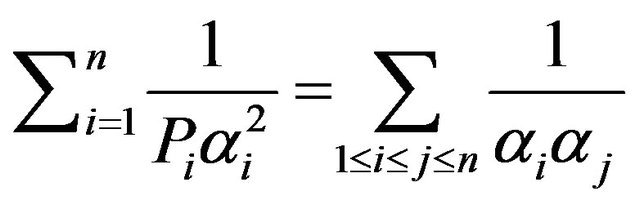 and
and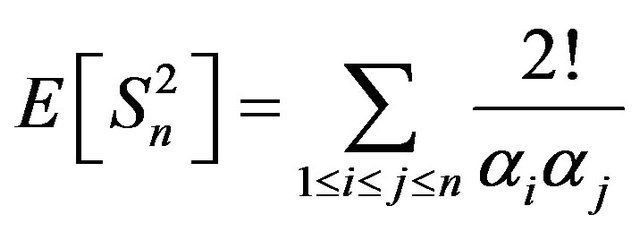 .
.
In Proposition 2, we found the first  derivative of
derivative of 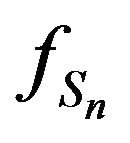 at 0, However to find higher order derivaties we recall Equation (2), that shows a direct relation between the
at 0, However to find higher order derivaties we recall Equation (2), that shows a direct relation between the  derivative
derivative 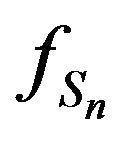 and
and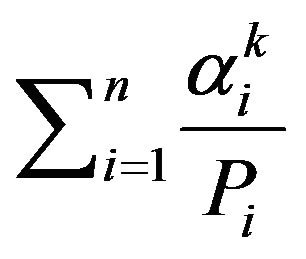 . Hence, in the next propostion we shall use Propostion 5, to find an equation for
. Hence, in the next propostion we shall use Propostion 5, to find an equation for  by finding a relation between
by finding a relation between 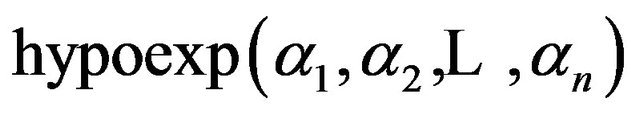 and
and 
Proposition 6. Let  and
and . Then
. Then
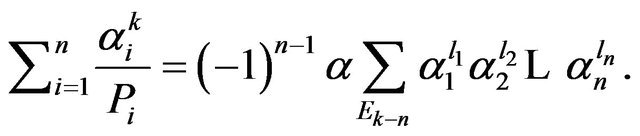
Proof. Let  and
and
 Then by Theorem 1, the pdf of
Then by Theorem 1, the pdf of  is
is
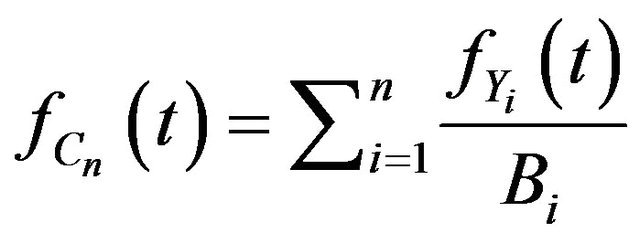
where 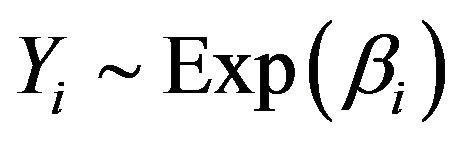 and
and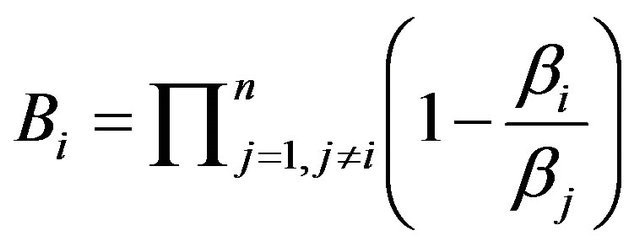 .
.
Next, we shall find 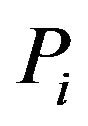 in terms of
in terms of . We have
. We have
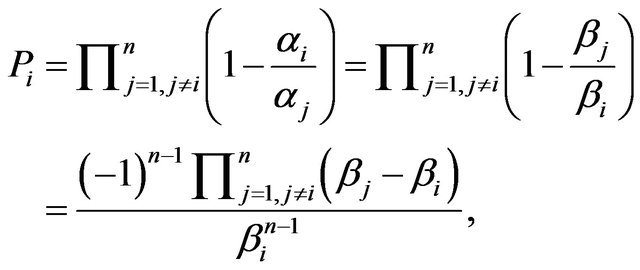
multiplying in the numerator and denominator by
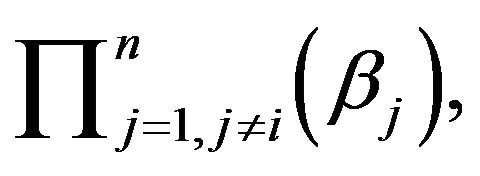 we obtain
we obtain 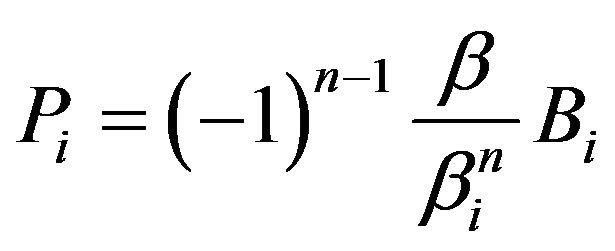 where
where 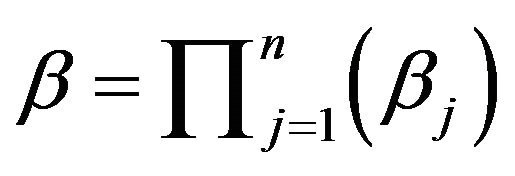 . Hence, we may write
. Hence, we may write
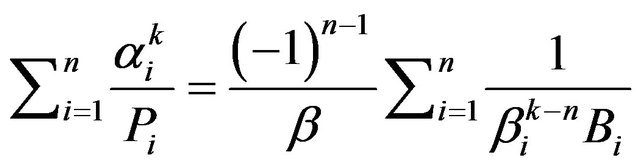 .
.
But, for  Proposition 5 gives that
Proposition 5 gives that
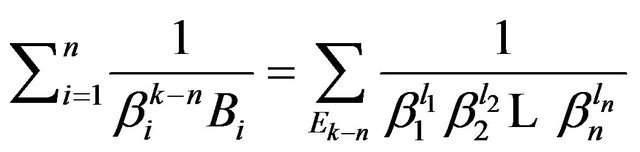 .
.
Therefore,
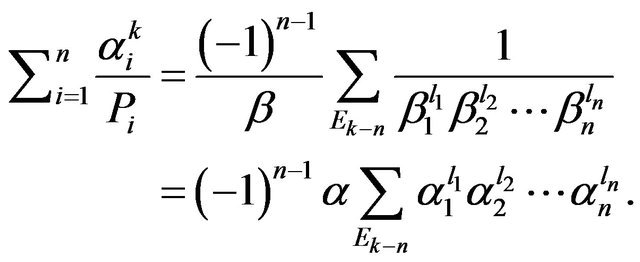

Proposition 7. Let  and
and . Then
. Then
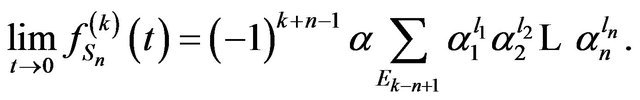
Proof. We have from Equation (2),
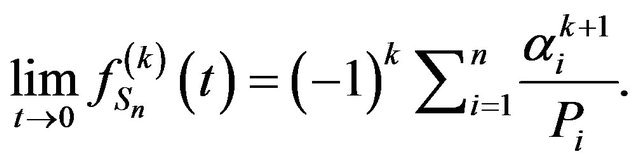
and from Proposition 6,

for 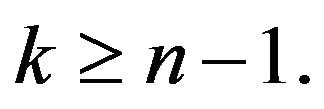 Then,
Then,
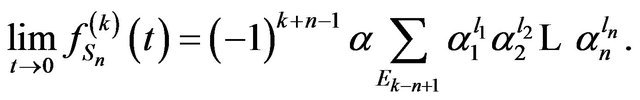

Many authors used the identity
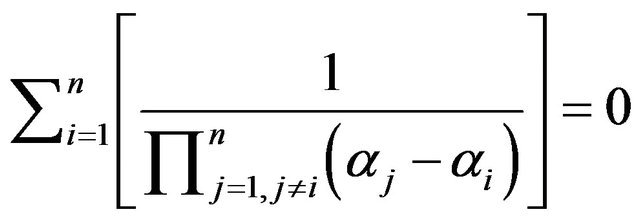
and proved it in many long and complicated methods. Here we shall submit a more simple prove. In addition, we shall find more related identities using the above results.
Proposition 8. Let  Then
Then
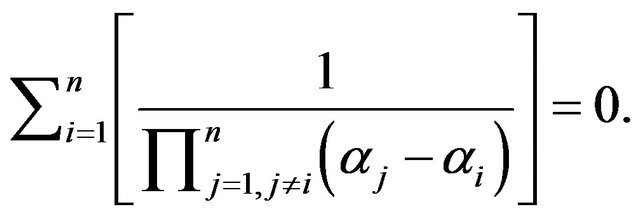
Proof. Let . By Corollary 1, taking
. By Corollary 1, taking  we have
we have  then
then
 .
.
However,
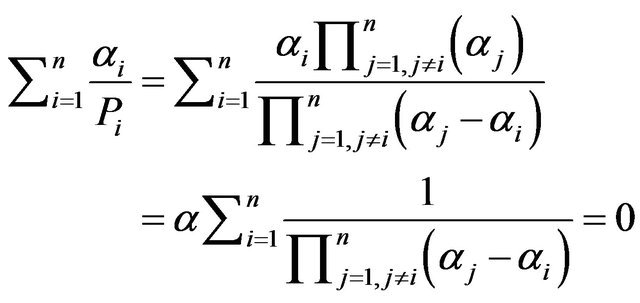
Therefore,


Next we shall find a more general equality using our previous results.
Proposition 9. Let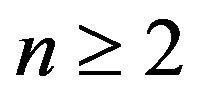 . Then
. Then
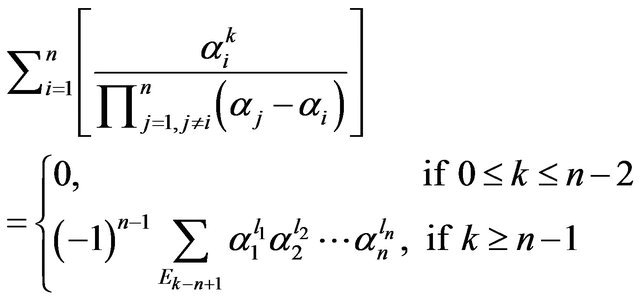
Proof. Let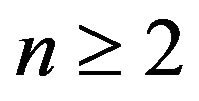 . Then,
. Then,
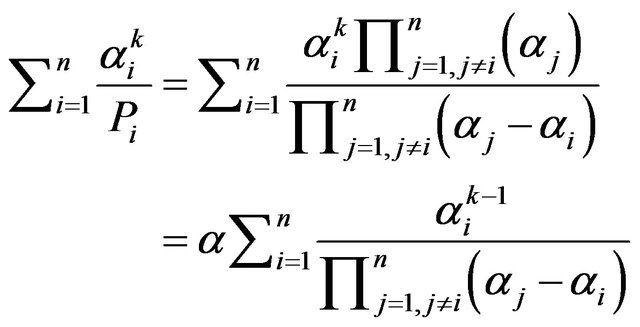 (5)
(5)
Suppose that . We have from Corollary 1,
. We have from Corollary 1,
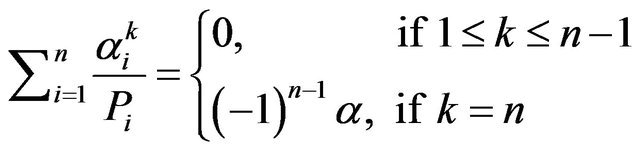
and Equation (5) gives that
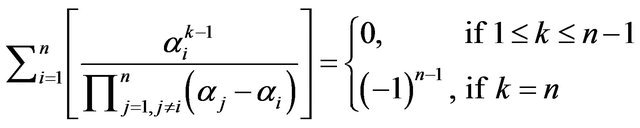
Replace 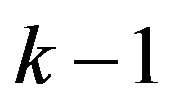 with
with 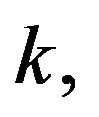 we obtain the first case and the case when
we obtain the first case and the case when  where
where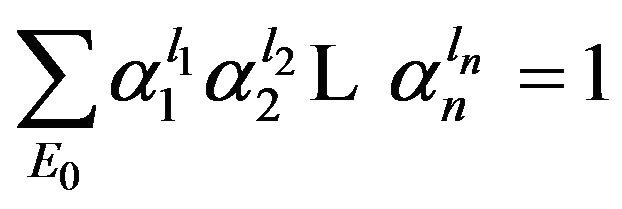 .
.
Now, suppose . By Proposition 6,
. By Proposition 6,
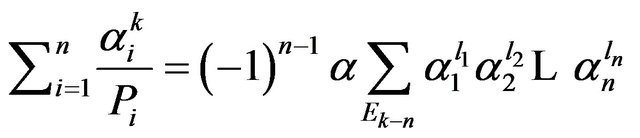
and the Equation (5) gives that
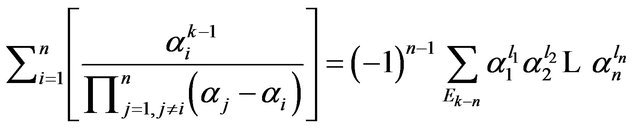 .
.
Also, replace 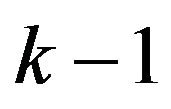 by
by  we obtain the last case when
we obtain the last case when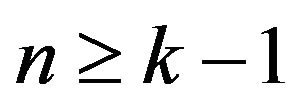 .
. 
5. The Main Results
We summarize Proposition 2 and 7 in the following theorem.
Theorem 2. Let 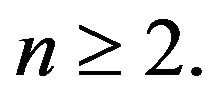 Then
Then
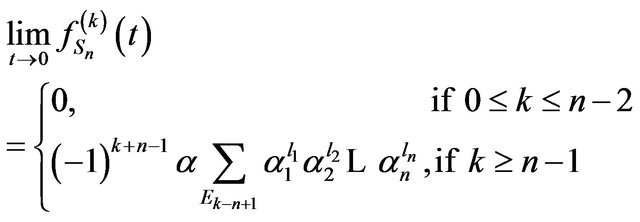
Also Corollary 1 and Proposition 5 and 6 can be summarized in the following theorem.
Theorem 3. Let 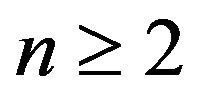 and
and . Then 1)
. Then 1) 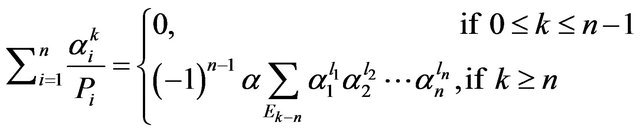
and 2) 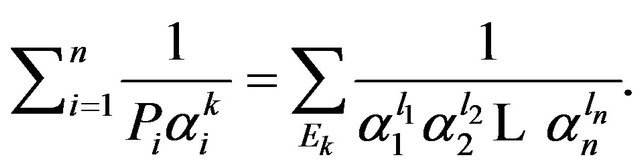
We recall Propostion 9 in the following corollary of Theorem 3.
Corollary 3. Let . Then
. Then
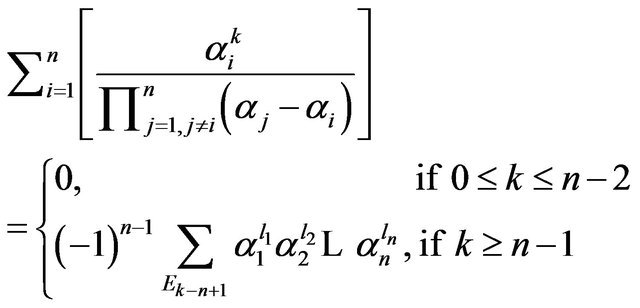
6. Case of Arithmetic and Geometric Parameters
The study of reliability and performance evaluation of systems and softwares use in general sum of independent exponential R.V. with distinct parameters. The model of Jelinski and Moranda [14], considered that the parameters changes in an arithmetic sequence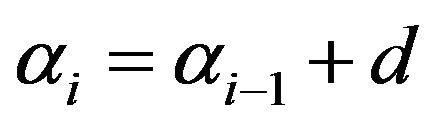 . Moreover, Moranda [15], considered the model when
. Moreover, Moranda [15], considered the model when 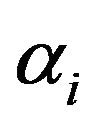 changes in an geometric sequence
changes in an geometric sequence . In this section, we study the hypoexponential in these two cases when the parameters are arithmetic and geometric, and we present their pdf.
. In this section, we study the hypoexponential in these two cases when the parameters are arithmetic and geometric, and we present their pdf.
6.1. Case of Arithmetic Parameters
We first consider the case when  form an arithmetic sequence of common difference
form an arithmetic sequence of common difference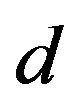 .
.
Lemma 2. For all 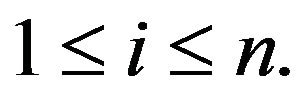
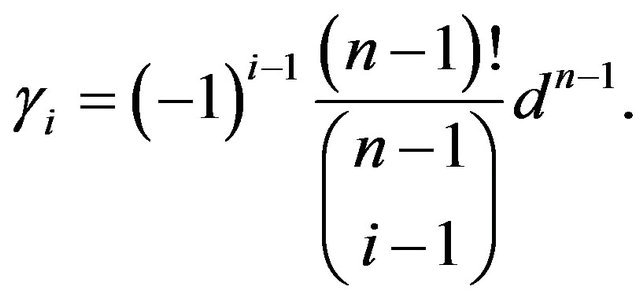
Proof. Suppose that 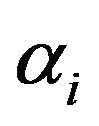 form an arithmetic sequence of common difference
form an arithmetic sequence of common difference . Then
. Then  We have
We have
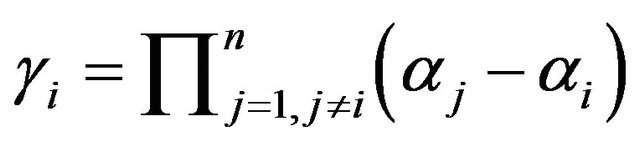 .
.
Hence,
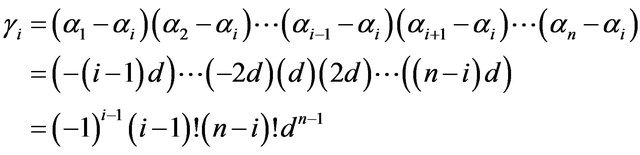
However,
 .
.
Then
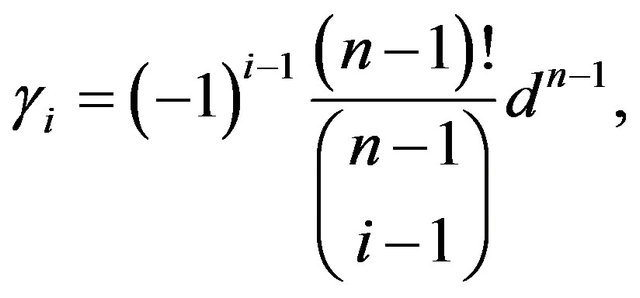

Lemma 3. For all 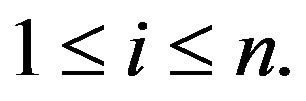
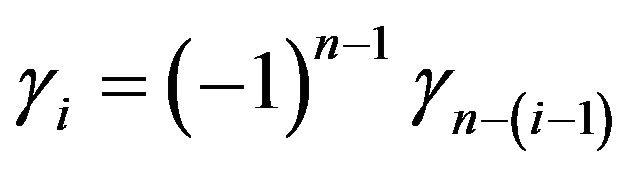 .
.
Proof. We have from Lemma 2,
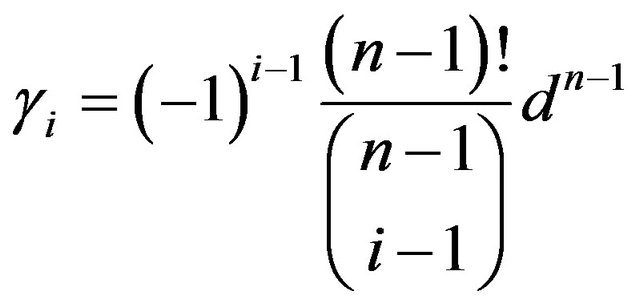
for all  Replace
Replace 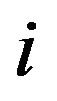 by
by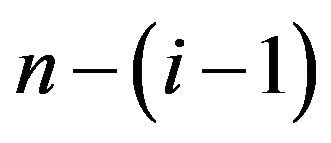 , we obtain
, we obtain
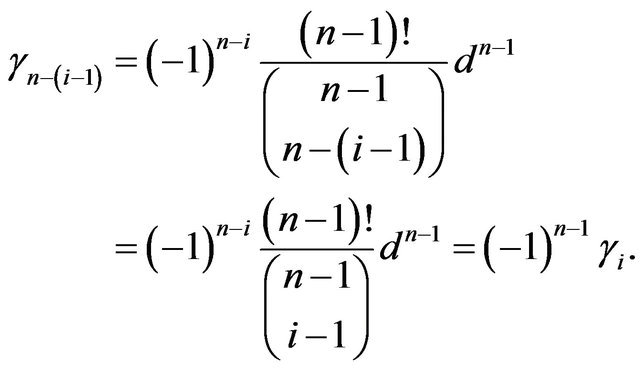
Thus we obtain the result. 
Proposition 10. Let  Then
Then
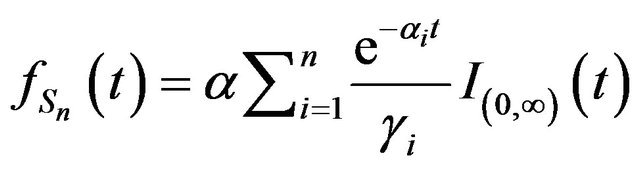 where
where

for all 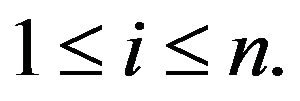
Proof. We have from Theorem 1
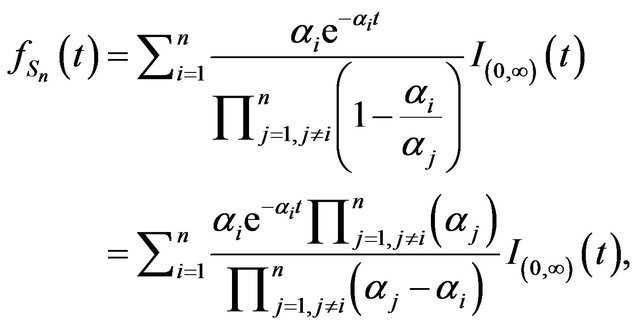
that can be written as
 where
where 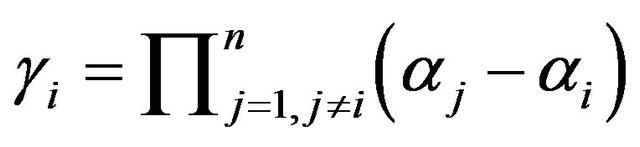 and by the Lemmas 2 and 3 we obtain the result.
and by the Lemmas 2 and 3 we obtain the result. 
6.2. Case of Arithmetic Parameters
Next, we consider the case when  form a geometric sequence of common ratio
form a geometric sequence of common ratio .
.
Proposition 11. Let 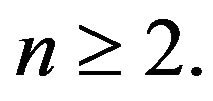 Then
Then
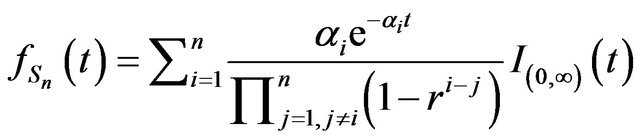 .
.
Proof. We have from Theorem 1,
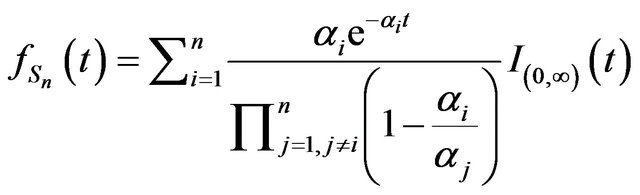 .
.
Suppose now the parameter 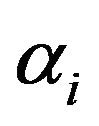 form geometric sequence of common ratio
form geometric sequence of common ratio . Then
. Then  and
and
 .
. 
We may also note that the equalities obtained for  represent here a special case and worth mentioning such as
represent here a special case and worth mentioning such as
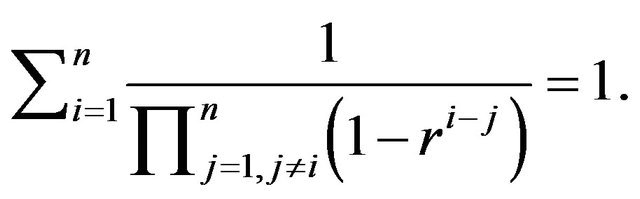
7. Conclusion
The pdf and cdf and some related properties of the hypoexponential distribution with distinct parameters were established. The proofs have been done by using Laplace transform and moment generating function technique. Also with the help of some known computational theorems as Heaviside expansion theorem and multinomial expansion formula the kth order derivative of  and the moment of this distribution of order k were established, in addition for some new related equalities. Eventually, the pdf for models when the parameters
and the moment of this distribution of order k were established, in addition for some new related equalities. Eventually, the pdf for models when the parameters  are arithmetic and geometric were presented. However the other two cases for hypoexponential distribution when the parameters are equal or not all equal can be studied and observed for future studies. It may be checked if they have the same properties as in this paper.
are arithmetic and geometric were presented. However the other two cases for hypoexponential distribution when the parameters are equal or not all equal can be studied and observed for future studies. It may be checked if they have the same properties as in this paper.