Small-Angle X-Ray Scattering of Amorphous Germanium: Numerical Modeling ()
1. Introduction
Amorphous semiconductors have been the subject of extensive experimental and theoretical investigations. Most of the interest has been focused on the tetrahedrally-coordinated amorphous germanium (a-Ge) due to its simple chemical bonding and composition on the one hand, and its potential applications in the fields of microelectronics and energy-conversion technologies on the other hand. As with all materials, the microstructure controls the electrical as well as the optical properties, so understanding and controlling the structure of a-Ge is crucial to its technological applications.
Unlike the crystalline phase, there is no experimental technique available that can determine the coordinates of atoms in a-Ge. Direct experimental data about atomic structure in amorphous materials were essentially limited to structure factors derived from X-ray, electrons, or neutron diffraction experiments [1]. Conventional diffraction measurements, principally, show that a-Ge, and other materials that form covalent tetrahedrally bonded crystals maintain the same pattern of four nearest neighbors in the amorphous phase, but do not have the long-range translational order that leads to sharp diffraction peaks. Smallangle scattering experiments performed on some a-Si and a-Ge films have shown a rapid increase of the scattered intensity as the scattering vector goes to zero [2-11]. Moreover, the shape and the magnitude of this small-angle scattering are found to be strongly dependent on the growth conditions and change after processing steps such as annealing or light illumination [12,13]. It is well known that such feature in the small-angle scattering data mirrors the heterogeneity of the amorphous material at the nanoscale. By correlating small-angle scattering results with those derived from other experiments [14-20], the mass-density measurements principally [19], many authors have postulated the existence of nanovoids in a-Si and a-Ge films. Indeed, such structural inhomogeneities are commonly believed to result in the mass-density of a-Si and a-Ge being lower than their corresponding crystalline phases; they also generate significant fluctuations in the density at the nanoscale which can be at the origin of the intense small-angle scattering in these materials. Many attempts have been made to analyze quantitatively the small-angle scattering data in a-Si and a-Ge. Using theoretical laws established previously [21], some characteristics of the nanovoids in these amorphous materials, such as size distribution, shape and number density, have been deduced from small-angle scattering data.
Numerical modeling technique has been widely used to simulate the structure of a-Ge. Most of the effort has been devoted to the analysis of its homogeneous structure; the generally accepted topological model is the socalled continuous random network (CRN). In this model, the main building blocks of the material are the same as in its crystalline counterpart, i.e. tetrahedra of Ge, but unlike in a perfect crystal, these blocks can be randomly oriented and connected, allowing “play” in atomic bondlengths and angles. Several approaches have been proposed for representing a homogenous tetrahedrally coordinated CRN models (see [22-24] and references therein). Most of these networks successfully reproduce the socalled wide-angle scattering data, i.e. for scattering vectors upper than 1 Å−1. Some numerical simulations dealing with nanovoids in a-Si have been also reported in the literature [25-31], but only two, to the best of our knowledge, are interested in the small-angle scattering [25,26]. Biswas et al. [25] were the first to demonstrate that CRN in which nanovoids are created accounts for the intense small-angle scattering, without altering the wide-angle scattering pattern. In our previous work [26], we have shown that CRN model containing nanocrystallites, called paracrystalline model [31], does not realize the intense small-angle scattering; paracrystalline networks containing nanovoids, on the other hand, account for the massdensity deficit and also the small-angle scattering feature observed experimentally. Due to computational limitations, unfortunately, relatively small atomistic models have been examined. However, it is well known that the small-angle scattering pattern is very sensitive to the model size. Indeed, the finite size of the structure imposes a scattering-vector threshold ( , where L is the size of the model), a features broadening, and also results in spurious ripples in the scattered intensity. Increasing the size of the atomistic model allows pushing down the scattering-vector threshold and reduces the amplitude of the ripples. Recently, Graff and Thorpe [32] have used a very large CRN model (105 atoms) to simulate the long-wavelength limit of the structure factor of amorphous silicon. Despite this huge model size, however, the scattering-vector threshold has moved very little (0.05 Å−1 vs 0.1 Å−1 for 4096-atom model), and the most remarkable is the persistence of the small-angle spurious ripples in the structure factor. The question that arises is then: how to make a good estimate of the scattered intensity free of finite model-size effects?
, where L is the size of the model), a features broadening, and also results in spurious ripples in the scattered intensity. Increasing the size of the atomistic model allows pushing down the scattering-vector threshold and reduces the amplitude of the ripples. Recently, Graff and Thorpe [32] have used a very large CRN model (105 atoms) to simulate the long-wavelength limit of the structure factor of amorphous silicon. Despite this huge model size, however, the scattering-vector threshold has moved very little (0.05 Å−1 vs 0.1 Å−1 for 4096-atom model), and the most remarkable is the persistence of the small-angle spurious ripples in the structure factor. The question that arises is then: how to make a good estimate of the scattered intensity free of finite model-size effects?
In the present work we reexamine the structural properties of atomistic models for a-Ge with nanovoids. We pay particular attention to the X-ray small-angle scattering. We consider structural models larger and more realistic than those considered in our previous work. We propose a simple way to get rid of finite model-size effects. A quantitative analysis of the estimated small-angle X-ray scattering is performed and comparison with available experimental data is made.
2. Computation Method
The present investigations are based on the class of CRN models generated with the Wooten-Winer-Weaire bondswitching algorithm by Barkema and Mousseau [23], resulting in N-atom models with periodic boundary conditions. 4096-atom models are provided to us by the courtesy of Normand Mousseau. To generate voids in the preceding amorphous network, a cluster of atoms is removed within a prescribed volume centered on a site selected at random. By choosing the centers of the voids to be sufficiently far apart, a number of non-overlapping voids are then constructed. After this, the dangling bonds, thus created on the void surface, are rebonded; in practice, the reconstruction of dangling bonds that would produce an unrelaxed bond of length greater than the second-neighbor distance (4 Å) and four-membered rings is rejected.
In order to obtain the equilibrium coordinates of these structures, a relaxation procedure is needed to minimize the deformation energy of the system. In the present work, the anharmonic Keating model proposed by Rücker and Methfessel [33] was used. Within the framework of this model, the strain energy of the system is given by:
 (1)
(1)
The first sum in this expression is on all atoms i in the supercell and their nearest-neighbors specified by j. The second sum is on all atoms i and pairs of distinct neighbors.  and
and 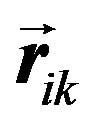 are the vectors connecting atom i with its first-neighbors j and k, respectively. R0 = 2.45 Ǻ is the unstrained length of the Ge-Ge bond. The force constants α and β essentially describe the bond-stretching and bond-bending restoring forces, respectively. Their dependence laws are given by [33]:
are the vectors connecting atom i with its first-neighbors j and k, respectively. R0 = 2.45 Ǻ is the unstrained length of the Ge-Ge bond. The force constants α and β essentially describe the bond-stretching and bond-bending restoring forces, respectively. Their dependence laws are given by [33]:
 (2)
(2)
The force constants α0 and β0 are treated as empirical parameters; they have been fixed at their crystalline values 42.09 N∙m−1 and 5.72 N∙m−1, respectively [34]. The total strain energy given by Equation (1) was minimized by an iterative conjugate gradient method. In this relaxation procedure, variations of the supercell sizes are allowed.
Now, given the equilibrium coordinates of all the atoms of the relaxed network, its structural characteristics can be easily computed such as the pair correlation function, the average bond-length, the average bond-angle, the average coordination number, the macroscopic mass density and the static structure factor. The partial pair correlation function, g(r), is defined by the relationship:
 (3)
(3)
where dn(r) is the average number of atoms lying within the spherical shell of radii r and r + dr centered at an atom taken as the origin, and n0 is the macroscopic number density of the model. Given the finite sizes of our structural models, their computed g(r)s are corrected for the supercell size effects. From the computed g(r) we deduce an important structural characteristic of a-Ge, which is directly obtainable from scattering experiments, namely the reduced scattering intensity, F(k), or the structure factor, S(k), defined as:
 (4)
(4)
where G(r), called the reduced radial distribution function, is defined by:
 (5)
(5)
The integral in Equation (4) reminds us of the onedimensional Fourier sine transform of G(r). This transformation between real and reciprocal spaces is only perfect if G(r) is known for an infinite range of r values; in practice, this is obviously not the case and the data are terminated at some finite . This is equivalent to G(r) being multiplied by a modification function, M(r), where M(r) = 1 for
. This is equivalent to G(r) being multiplied by a modification function, M(r), where M(r) = 1 for  and 0 for
and 0 for ; the effective result is thus:
; the effective result is thus:
 (6)
(6)
or, in a more condensed form:
 (7)
(7)
where  is the Fourier cosine transform of M(r) and * stands for he convolution product. This leads to the introduction of termination errors in the “perfect” Fourier transform F(k), which for the step-function M(r) given above is equivalent to features in F(k) being convoluted with the Fourier cosine transform of M(r), i.e. the sinc function
is the Fourier cosine transform of M(r) and * stands for he convolution product. This leads to the introduction of termination errors in the “perfect” Fourier transform F(k), which for the step-function M(r) given above is equivalent to features in F(k) being convoluted with the Fourier cosine transform of M(r), i.e. the sinc function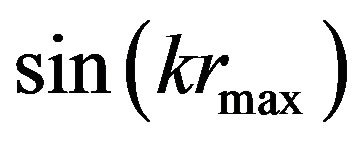 . The effect of this is twofold: a loss in resolution is incurred since wave-numbers in reciprocal space less than
. The effect of this is twofold: a loss in resolution is incurred since wave-numbers in reciprocal space less than 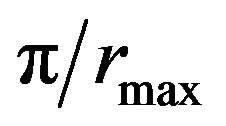 are lost, resulting in a features broadening of
are lost, resulting in a features broadening of , and spurious termination ripples at values
, and spurious termination ripples at values 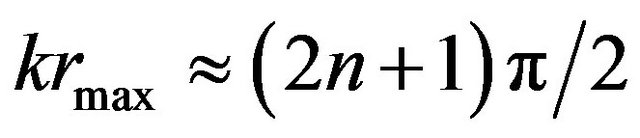 are introduced (where n is an integer), which decay with increasing k.
are introduced (where n is an integer), which decay with increasing k.
Increasing  these ripples migrate down but at the expense of an increase in amplitude. The usual procedure used to minimize termination errors employs a damping factor which multiplies the finitely ranged G(r) in the Fourier transform [Equation (6)], replacing a sharp discontinuity at
these ripples migrate down but at the expense of an increase in amplitude. The usual procedure used to minimize termination errors employs a damping factor which multiplies the finitely ranged G(r) in the Fourier transform [Equation (6)], replacing a sharp discontinuity at  by a smoothly varying function. The most used factor is the Lorch function defined by [35]:
by a smoothly varying function. The most used factor is the Lorch function defined by [35]:
 (8)
(8)
This form reduces the termination ripples but at the expense of signal distortion such as broadening, reduction in the intensity and, most interestingly, downward shift. It should be noted here that these effects are noticeable in the range of small values of k, i.e. in the small-angle scattering range which interests us most in this work. Other sources of noise, always related to the finite size of the atomistic model, contribute to a supplementary contamination of this part of the signal. Indeed, a deviation, even infinitesimal, from the exact value of the macroscopic density of the atomistic model leads to additional spurious ripples along the scattering pattern; in addition, statistical errors arising from the computation of radial distribution function are reflected in the Fourier transform in extra wrinkles too. The reduced scattering intensity can then be reformulated as follows:
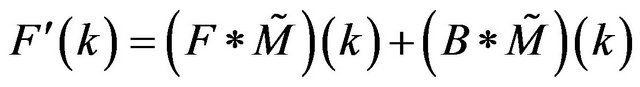 (9)
(9)
where the function B(k) reflects the noise we discussed above. The question one might ask at this level is how to estimate the function F(k) from ?
?
We limit ourselves here to the small-angle scattering range where one expects a monotonically varying intensity. The function B(k) can complicate the task if it had features reflecting correlations in r-space. But this is not the case, fortunately, in our problem. Indeed, the noise sources we discussed above relate to numerical problems and have nothing to do with the structural properties of the atomistic model in question. Thus, we expect that B(k) modulates the function  without any distortion. The problem of finding F(k) reduces then to a problem of smoothing the noisy data
without any distortion. The problem of finding F(k) reduces then to a problem of smoothing the noisy data . So, we propose a least square fitting procedure. It consists to, first, choose a function F(k), then, perform its convolution by
. So, we propose a least square fitting procedure. It consists to, first, choose a function F(k), then, perform its convolution by  and, finally, minimize the root-mean-square deviation between the convoluted function thus obtained and the raw data
and, finally, minimize the root-mean-square deviation between the convoluted function thus obtained and the raw data . It should be noted here that according to Equation (6) the function F(k) must be chosen to be odd. What form do we choose for F(k)?
. It should be noted here that according to Equation (6) the function F(k) must be chosen to be odd. What form do we choose for F(k)?
The choice of the form of F(k) is dictated in fact by that of the X-ray scattering intensity I(k), given that these two quantities are related to each other. Indeed, I(k) is expressed in terms of the reduced correlation function G(r) as follows [1]:
 (10)
(10)
where f(k) is the atomic scattering factor. Now, according to Equation (4), this relation can be rewritten as:
 (11)
(11)
which gives:
 (12)
(12)
A simple phenomenological model describing the dependence of f on the scattering vector for Ge atom is available [34], viz.:
 (13)
(13)
with K1 = 31.53, K2 = 0.13 and K3 = 2.10. For a homogenous structure such as the CRN, it is well established that I(k) decreases slowly toward “zero” as k tends to zero; thus, a polynomial form can be a good representation of the small-angle scattering intensity. Structural heterogeneities such as nanovoids in a homogenous matrix can be treated as nanoscatterers leading to smallangle scattering. In the limit of low concentrations, the small-angle scattering intensity is expected to obey the Guinier’s law [36]. For monodispersed scattering centers, this law gives:
 (14)
(14)
where RG, called the radius of gyration, represents the average size of electron density fluctuations in the material. For polydispersed widely separated centers, the relation (14) can be generalized as follows:
 (15)
(15)
Theoretically, the Guinier approximation is the asymptotic behavior of I(k) at very small values of k; it is usually valid at k-range such that . Beyond this limit, the expression of I(k) is unknown, but it is expected to be a simple monotonically decreasing function with increasing k. We propose here to reproduce the small-angle scattering intensity I(k) by a weighted sum of Gaussians that can be formulated as follows:
. Beyond this limit, the expression of I(k) is unknown, but it is expected to be a simple monotonically decreasing function with increasing k. We propose here to reproduce the small-angle scattering intensity I(k) by a weighted sum of Gaussians that can be formulated as follows:
 (16)
(16)
where ai can be positive or negative. The number N of the Gaussians and their characteristics 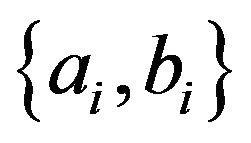 are adjustable parameters. Such form must give the Guinier’s law at very small k-values; moreover, we have verified that it reproduces very nicely simple polynomial functions and consequently the scattering intensity due to atomic centers at k < 1.5 Å−1.
are adjustable parameters. Such form must give the Guinier’s law at very small k-values; moreover, we have verified that it reproduces very nicely simple polynomial functions and consequently the scattering intensity due to atomic centers at k < 1.5 Å−1.
3. Results
The original CRN of Barkema and Mousseau [23] was first relaxed using the enharmonic Keating potential given by Equation (1). Next, voids of various size and concentration have been introduced into the preceding CRN. To prevent any correlation between the inclusions, the nanovoids are choosen sufficiently far apart and reduced in number. So, nine nanoporous networks for a-Ge (denoted hereafter by NPN) have been constructed with void volume fractions of practically 3% and 5%, and nanopores centers-separation greater than 24 Å. Finally, the obtained models are relaxed starting with initial configuration in which all the atoms in the supercell are randomly displaced from their positions in the CRN. More structural details of our nanoporous models are summarized in Table 1.
Standard measures of the short-range disorder for our structural models, characterized by the bond length, bond angle and dangling bonds density are given in Table 2. A measure of the mass density of the amorphous models is also reported in this table. The pair correlation functions computed for these structural nanoporous models as well as CRN model are reported in Figure 1. The corresponding reduced scattering intensities, 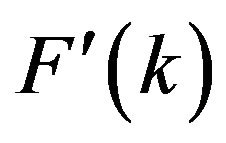 , have been computed according to the relation (6) in which the cutoff
, have been computed according to the relation (6) in which the cutoff  has been fixed at 30 Å for all the examined amorphous models. Two types of “modification function” M(r) have been used, namely the step function and the Lorch function. The results are displayed in Figure 2(a) for k values below 3 Å−1. These curves were fitted to the model function given by Equation (14) in the k-range extending from
has been fixed at 30 Å for all the examined amorphous models. Two types of “modification function” M(r) have been used, namely the step function and the Lorch function. The results are displayed in Figure 2(a) for k values below 3 Å−1. These curves were fitted to the model function given by Equation (14) in the k-range extending from  to 1.5 Å−1. The results of the best fits are displayed in Figure 2(b) by continuous lines superimposed on their corresponding
to 1.5 Å−1. The results of the best fits are displayed in Figure 2(b) by continuous lines superimposed on their corresponding  curves shown by dashed lines. Our fitting procedure is accomplished by gradually incrementing the number of Gaussians (N) by 1 from N = 1; at each step the rms deviation is minimized for all the 2N parameters starting with random values for aN and bN, and the values obtained in the preceding step for the first (2N−2) parameters. The procedure is stopped when the rms deviation stabilizes. The best fits shown in Figure 2(b) were obtained with rms values varying between 0.2 and 0.4.
curves shown by dashed lines. Our fitting procedure is accomplished by gradually incrementing the number of Gaussians (N) by 1 from N = 1; at each step the rms deviation is minimized for all the 2N parameters starting with random values for aN and bN, and the values obtained in the preceding step for the first (2N−2) parameters. The procedure is stopped when the rms deviation stabilizes. The best fits shown in Figure 2(b) were obtained with rms values varying between 0.2 and 0.4.
Table 1. The structural characteristics of the nanoporous atomistic models as-generated before relaxation.

(a)monodispersed spherical nanovoids; (b)polydispersed spherical nanovoids; (c)monodispersed arbitrarily oriented ellipsoidal nanovoids.
Table 2. Standard measures of the local disorder for the atomistic models as-generated after relaxation.

*Weighted diameter of gyration.
Once we have the estimated function F(k) we can now easily deduce the estimated scattering intensity per atom, I(k), according to the relation (10). Figure 3 shows the fitted scattering intensities superimposed on their corresponding noncorrected ones for the CRN and the six nanoporous models based on it. For comparison, we have reported in this figure three available experimental data [2]. The characterization of the small-angle scattering in our nanoporous amorphous models has been performed by means of the Guinier plot of  versus k2 [36] and by the computation of the so-called “invariant” Q defined by [21]:
versus k2 [36] and by the computation of the so-called “invariant” Q defined by [21]:
 (17)
(17)
The integration in Equation (17) was truncated to 1 Å−1 for reasons which we will come back again later. The Guinier plots of  versus k2 for some nanoporous models are displayed in Figure 4. For comparison, we have reported in this figure two available experimental data [2]. The dependences of the “invariant” Q and the ratio
versus k2 for some nanoporous models are displayed in Figure 4. For comparison, we have reported in this figure two available experimental data [2]. The dependences of the “invariant” Q and the ratio 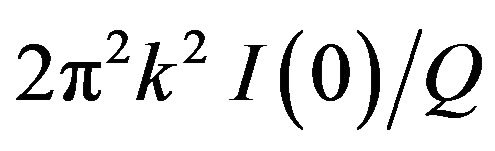 on the radius of gyration of the nanovoids are shown graphically in Figure 5.
on the radius of gyration of the nanovoids are shown graphically in Figure 5.
4. Discussion
4.1. The Structural Properties of the Atomistic Models
From the last column of Table 2, we stress that the nanoporous models are not hypothetical high energy configurations, but are energetically competitive with the starting CRN. The former present strain energies are somewhat greater than the bare CRN one. This small energy excess is reflected primarily in the bond-angle distortion. Indeed, as can be noted from the 3rd column of this table, the average bond-angle decreases slightly while the standard deviation varies in both senses relative to the CRN ones; the bond length distribution, by cons, is found to be insensitive to the presence of nanovoids in a-Ge model.

Figure 1. The pair correlation functions computed for the CRN model and six nanoporous models based on it. Traces are vertically offset by six for clarity. Inset: direct comparison between pair correlation functions of the CRN (blue) and the nanoporous model denoted by NPN7 (red) over the nanoscale range.
As shown in the 4th column of Table 2, the CRN relaxed with the anharmonic Keating potential is less dense than the crystalline phase by practically 2%. Incorporating nanovoids in the CRN leads to even further less dense amorphous phase. The density decreases with increasing void volume fraction, but it is practically independent on the nanovoid size. For amorphous models considered here, the density deficit with respect to the crystal varies between 2% and 10%, which is well within the range of measured values. In addition, the corresponding dangling bond densities, reported in the 5th column of Table 2, are of the same order of magnitude as those estimated from electron spin resonance measurements (see Ref. [2] and references therein).
Now we turn our attention to the pair correlation functions displayed in Figure 1. An overall inspection of this

Figure 2. (a) The raw reduced scattering intensities computed for the CRN model and six nanoporous models based on it, using the step function (dashed line) and the Lorch function (continuous line) as modification functions. Inset: direct comparison between the raw structure factors computed for the NPN6 model; (b) The corrected reduced scattering intensities (continuous line) superimposed on their corresponding raw data (dashed line). Inset: the noise function derived for the NPN6 model after correction.
figure shows that the g(r)s of nanoporous models are indistinguishable from that of the CRN. They reproduce very well the overall aspect of the experimentally derived pair correlation function for pure a-Ge over the experimentally accessible range 0 - 10 Å. They show that only the two first neighbor shells, at ~2.46 and ~4 Å, are well defined (firstand second-nearest neighbors, respectively). Beyond 5 Ǻ, the correlation between pairs of atoms becomes relatively much weaker, and virtually disappears from ~12 Å. A careful examination of this figure shows that nanoporous models exhibit a pair correlation function more intense than that of the CRN just over the pair-separation range of the order of the nanovoid radius. This fact is well illustrated in the inset showing a direct

Figure 3. The scattering intensities computed for the CRN model and six nanoporous models based on it: the data corrected for the finite size of the models (continuous line) are superimposed on their corresponding raw data (dashed line). Traces are vertically offset for clarity. Insets: (on the left) direct comparison of the SAXS patterns computed for the CRN (blue), the NPN1 (green) and NPN4 (red) models; (on the right) experimental SAXS data for electrodeposited (continuous line), sputtered (dashed line) and evaporated (dot-dashed line) a-Ge films (from Shevchik and Paul [2]).
comparison of the g(r)s computed for the CRN and one nanoporous model based on it denoted by NPN7 in Table 1; for clarity, only the intermediate pair-separation range was shown. The elevation of g(r) in this nanometer range particularly, will have considerable effects on the small-angle scattering as we will see later. It should be noted here that this result agrees with the finding of Opletal et al. [31] who used Monte Carlo methods to simulate the structure of porous a-Si.
4.2. X-Ray Scattering Patterns of the Atomistic Models
We arrive now to the reduced scattering intensities com-

Figure 4. Guinier plots of ln[I(k)] versus k2: (a) computed for nanoporous atomistic models for a-Ge denoted by NPN4, NPN6, NPN7 and NPN8; (b) and (c) measured for a-Ge films (from Shevchik and Paul [2]). The dashed lines represent the results of a linear regression fits. Insets: fractional void volume distributions.
puted for our structural models and shown in Figure 2(a). As we are concerned mainly with the small-angle scattering, only the data for small values of k were shown. Owing to the finite size of our structural models, the data are available for k > 0.1 Å−1. This figure illustrates well the truncation effects and the noise we discussed in the computation method section. The apparent effects are spurious ripples along the k-range. The use of damping function such as the Lorch function effectively reduces these spurious effects; the ripples disappear almost completely from the wide-angle scattering data, i.e. for k > 1 Å−1, but persist at very small values of k and increase in amplitude as k goes to zero. Moreover, a small downward shift of the small-angle features has been shown but it is more obvious in the computed structure factors  as illustrated in the inset of this figure.
as illustrated in the inset of this figure.
From this figure, we note that the wide-angle scatter-
 (a)
(a) (b)
(b)
Figure 5. (a) The Q-factor values computed for our nanoporous atomistic models for a-Ge with void volume fractions of ~3% (circles) and ~5% (triangles). The full and empty symbols refer to the members left and right of Equation (19), respectively. Each horizontal line represents the Q value computed by taking the average of the void volume fractions and the average of the electron density deficits of the corresponding nanoporous atomistic models; (b) The 2π2I(0)/Q values computed for our nanoporous atomistic models for a-Ge. The continuous line is the result of a linear regression fit.
ing data are practically insensitive to the presence of voids in a-Ge network. This is not the case, however, for the small-angle scattering data. Indeed, despite the spurious ripples, one can identify an evolution of the overall aspect of 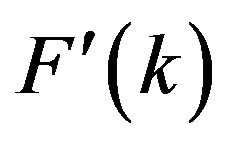 at small k-values by introducing nanovoids of progressive size and concentration in the CRN. One can foresee, in particular, a large feature that grows in the range 0 - 0.5 Å−1 with increasing the void size and/or the void volume fraction. This expected smallangle feature, free of truncation errors and noise, has become more evident through our Gaussians fitting procedure whose results are displayed in Figure 2(b). The Gaussians fitting procedure has been also applied to the voidless CRN model; the result is shown in the bottom of this figure. An excellent agreement with what one would expect for a homogeneous monoatomic amorphous structure is thus obtained. More interestingly, applied independently to the raw scattering data obtained with the step function and those obtained with the Lorch function, the Gaussians fitting procedure gives virtually indistinguishable results. In order to check the validity of the hypotheses that we have made about the sources of noise, we have computed the difference
at small k-values by introducing nanovoids of progressive size and concentration in the CRN. One can foresee, in particular, a large feature that grows in the range 0 - 0.5 Å−1 with increasing the void size and/or the void volume fraction. This expected smallangle feature, free of truncation errors and noise, has become more evident through our Gaussians fitting procedure whose results are displayed in Figure 2(b). The Gaussians fitting procedure has been also applied to the voidless CRN model; the result is shown in the bottom of this figure. An excellent agreement with what one would expect for a homogeneous monoatomic amorphous structure is thus obtained. More interestingly, applied independently to the raw scattering data obtained with the step function and those obtained with the Lorch function, the Gaussians fitting procedure gives virtually indistinguishable results. In order to check the validity of the hypotheses that we have made about the sources of noise, we have computed the difference  which must give, according to the Equation (9), the expected noise function convoluted by the Fourier transform of the corresponding modification function, i.e.
which must give, according to the Equation (9), the expected noise function convoluted by the Fourier transform of the corresponding modification function, i.e. . The inset of Figure 2(b) shows one result corresponding to the nanoporous model NPN7; the same aspect is observed with the other models. We obtain thus, as expected, a function that oscillates symmetrically about zero and is quickly damped when k increases from zero. The two last results provide support for our formulation of the problems of truncation and noise expressed by Equation (9), as well as the proposed Gaussians fitting procedure.
. The inset of Figure 2(b) shows one result corresponding to the nanoporous model NPN7; the same aspect is observed with the other models. We obtain thus, as expected, a function that oscillates symmetrically about zero and is quickly damped when k increases from zero. The two last results provide support for our formulation of the problems of truncation and noise expressed by Equation (9), as well as the proposed Gaussians fitting procedure.
Usually in a many-particles scattering problem, interference phenomena are expected to be observed in the scattering pattern. Our simulated scattering patterns displayed in Figure 2(a) don’t show any interference. Indeed, if there were interferences, the shape of the scattered intensity and its amplitude must vary considerably between models with nanopores of same size but in different numbers. This is not the case, however, as can be deduced from the comparison of NPN2 and NPN5 scattering patterns (shown in Figure 2) or those of NPN1 and NPN4 models (not shown). As a matter of fact, interferences exist but, for the choosen nanopores centers-separation of 24 Å, they manifest themselves below ~0.1 Å−1 and so not accessible by our finite size structural models. These observations lead us to assert that the estimated reduced scattering intensities F(k) on the 0 - 1 Å−1 k-range are devoid of interference phenomena.
We now turn to the discussion of the computed scattering intensities I(k) displayed in Figure 3. This figure shows, for each structural model, the scattered intensity derived from the fitted interference function F(k) superimposed on that deduced from the raw data . This comparison highlights the dramatic effect of the finite size of the structural model on the scattering intensity at small values of k. As can be seen in this figure, only the SAXS is affected by the presence of nanovoids in a-Ge. A direct comparison between the SAXS patterns of the CRN and two nanoporous networks are shown in the inset (on the left) of this figure. As expected for a homogeneous structure of a-Ge, I(k) decreases monotonically to zero as k goes to zero. More interestingly, the scattering intensity in this case does not vanish at 1 Å−1, contrary to what is expected. In presence of nanovoids in a-Ge networks, the scattering intensity increases rapidly from 1 Å−1 practically and tends to a finite value at k = 0. The latter is found to increase rapidly with increasing the void size and/or the void volume fraction. The SAXS due to nanovoids in a-Ge overlap thus with the scattering by atomic centers of the host matrix, but do not exceed 1 Å−1.
. This comparison highlights the dramatic effect of the finite size of the structural model on the scattering intensity at small values of k. As can be seen in this figure, only the SAXS is affected by the presence of nanovoids in a-Ge. A direct comparison between the SAXS patterns of the CRN and two nanoporous networks are shown in the inset (on the left) of this figure. As expected for a homogeneous structure of a-Ge, I(k) decreases monotonically to zero as k goes to zero. More interestingly, the scattering intensity in this case does not vanish at 1 Å−1, contrary to what is expected. In presence of nanovoids in a-Ge networks, the scattering intensity increases rapidly from 1 Å−1 practically and tends to a finite value at k = 0. The latter is found to increase rapidly with increasing the void size and/or the void volume fraction. The SAXS due to nanovoids in a-Ge overlap thus with the scattering by atomic centers of the host matrix, but do not exceed 1 Å−1.
A comparison with available SAXS data has been made in this figure. The inset shows three measured scattering patterns reported by Shevchik and Paul [2] for a-Ge films grown by three different methods such as evaporation, electrodeposition and sputtering. The experiment shows clearly that the SAXS depends on the preparation method. This variation is well accounted for by our structural models. More interestingly, the overall aspect of experimental SAXS curves is well realized by our simulation data corrected for termination errors and noise. This finding thus provides support for our Gaussians fitting procedure. Moreover, it leads us to assert that the structure of electrodeposited film is closer to a continuous random network, while those of sputtered and evaporated films are rather nanoporous. Even more, the sizes of nanovoids in sputtered films cannot exceed those considered in our present simulation, but they surpass many in evaporated films. In fact, Shevchik and Paul [2] have reported largest void radius of 2 Å, 5 Å and 40 Å for electrodeposited, sputtered and evaporated a-Ge, respectively.
4.3. Quantitative Analysis of the SAXS Patterns
Our simulated SAXS patterns adjusting for the effects of truncation and noise are now ready for a rigorous quantitative analysis. The Guinier plots of  versus k2 are displayed in Figure 4, whereas the computed invariant Qs and the ratios
versus k2 are displayed in Figure 4, whereas the computed invariant Qs and the ratios 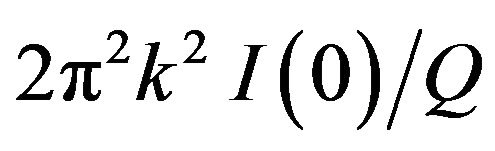 are shown graphically in Figures 5(a) and (b), respectively. As can be noted from Figure 4(a), the Guinier plots reveal linear relationships over a limited k-range close to zero. A linear regression fit of each data,
are shown graphically in Figures 5(a) and (b), respectively. As can be noted from Figure 4(a), the Guinier plots reveal linear relationships over a limited k-range close to zero. A linear regression fit of each data, 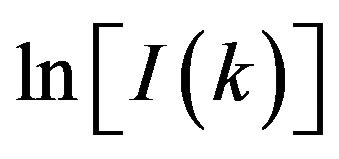 versus k2, is performed over the same k-range (0 - 0.447 Å−1) and the results are shown by dashed lines in the same figure. From this comparison, we note that the extent of the range on which the relation is linear depends on the void size; it shrinks with increasing void size. The maximum extent corresponds thus to the smallest void size detectable by SAXS measurements. As we will show in the following, this corresponds practically to the smallest void radius examined in our present work, i.e. ~5 Å. We expect thus a maximum extent of ~0.7 Å−1. From the results of the linear regression fits, and according to Equation (14), the diameters of gyration (2RG) in our nanoporous models with monodisperse distribution of nanovoids were extracted and reported in the 6th column of Table 2. For comparison, we have reported in the same column the diameters of gyration corresponding to the starting void diameters reported in Table 1. As shown in this column, the diameters of gyration after structural relaxation are smaller than their corresponding values before. In addition, this finding holds for spherical as well as ellipsoidal nanovoids. Therefore, the relaxation of nanoporous structures results in a significant compression in the volume of the individual voids. We can stress then that voids in a-Ge with diameter smaller than 10 Å will dissolve practically after relaxation leading so to a no detectable SAXS.
versus k2, is performed over the same k-range (0 - 0.447 Å−1) and the results are shown by dashed lines in the same figure. From this comparison, we note that the extent of the range on which the relation is linear depends on the void size; it shrinks with increasing void size. The maximum extent corresponds thus to the smallest void size detectable by SAXS measurements. As we will show in the following, this corresponds practically to the smallest void radius examined in our present work, i.e. ~5 Å. We expect thus a maximum extent of ~0.7 Å−1. From the results of the linear regression fits, and according to Equation (14), the diameters of gyration (2RG) in our nanoporous models with monodisperse distribution of nanovoids were extracted and reported in the 6th column of Table 2. For comparison, we have reported in the same column the diameters of gyration corresponding to the starting void diameters reported in Table 1. As shown in this column, the diameters of gyration after structural relaxation are smaller than their corresponding values before. In addition, this finding holds for spherical as well as ellipsoidal nanovoids. Therefore, the relaxation of nanoporous structures results in a significant compression in the volume of the individual voids. We can stress then that voids in a-Ge with diameter smaller than 10 Å will dissolve practically after relaxation leading so to a no detectable SAXS.
It is known that the Guinier approximation is usually valid at k-range such that RGk < 1 [21,34]. Our present simulation shows, however, that this law holds even well beyond this limit. For the largest nanopores examined in our present work, this limit reaches 2. It is worthwhile to note here that several of the small-angle scattering studies on a-Si and a-Ge also fitted data with the Guinier form in the angular region where RGk > 1 (see Refs. [7,11] and references therein). Our findings are therefore a support to these experimental works.
A comparison with available experimental SAXS data has been made in this figure. In Figures 4(b) and (c) we have reported the Guinier plots of the measured SAXS patterns for a-Ge films already shown in Figure 3. Both data show a different behavior. Only the former is apparently in agreement with our simulation data. It shows, indeed, a linear behavior over a relatively wide range extending from ~0 to ~0.4 Å−1. Void radius of gyration of 3.8 Å is deduced for the sputtered a-Ge film. The data of evaporated a-Ge film [see Figure 4(c)], however, don’t show a linear behavior over the explored 0 - 0.4 Å−1 k-range. This nonlinearity is usually attributed to a polydisperse void size distribution in the sample. The data were accounted for theoretically by a distribution of Guinier intensities according to the following relation [3]:
 (18)
(18)
where M(RG) is the volume fraction of the voids with radius of gyration RG. The derived fractional void volume distribution is reported in the inset of Figure 4(c). The latter reflects the occurrence of many void radii of gyration between 10 and 40 Å in the examined a-Ge film. To check this argument, we have generated a nanoporous structure of a-Ge with a “polydisperse” void size distribution, denoted by NPN8 in Table 1. The corresponding Guinier plot of 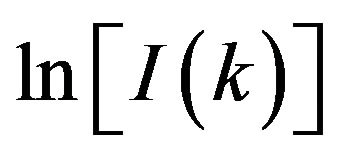 versus k2 is shown in the top of Figure 4(a), together with the result of its regression linear fit. A neat deviation from linearity can be noted from this curve, when compared with the other curves in the same figure. Using now a least-squares procedure we have derived M(RG) by fitting the simulated scattering intensity to the empirical one given by Equation (18); the result is shown in the top inset of Figure 4(a). As expected, the latter shows a bimodal void size distribution. More importantly, the two characteristic radii of gyration, 3.0 and 5.5 Ǻ, in this distribution as well as their weights are in close agreement with their corresponding theoretical values. Applied to nanoporous models with monodisperse void size distributions, this procedure gave the distributions reported in the insets of Figure 4(a). The latter clearly show the expected monodisperse void size distributions. Our findings are thus in favor of the quantitative analysis of SAXS data using the empirical law expressed by the Equation (18).
versus k2 is shown in the top of Figure 4(a), together with the result of its regression linear fit. A neat deviation from linearity can be noted from this curve, when compared with the other curves in the same figure. Using now a least-squares procedure we have derived M(RG) by fitting the simulated scattering intensity to the empirical one given by Equation (18); the result is shown in the top inset of Figure 4(a). As expected, the latter shows a bimodal void size distribution. More importantly, the two characteristic radii of gyration, 3.0 and 5.5 Ǻ, in this distribution as well as their weights are in close agreement with their corresponding theoretical values. Applied to nanoporous models with monodisperse void size distributions, this procedure gave the distributions reported in the insets of Figure 4(a). The latter clearly show the expected monodisperse void size distributions. Our findings are thus in favor of the quantitative analysis of SAXS data using the empirical law expressed by the Equation (18).
Now we conclude our discussion with the computed Q-factors and the ratios  displayed graphically in Figure 5 as functions of the void radius of gyration. The Q values are obtained from Equation (17) in which the integral was truncated to k = 1 Ǻ−1. This choice is now obvious, because in our above discussion we have seen that this value represents the cut-off of the SAXS in a-Ge. As expected, the computed Q-factor is practically independent on the void radius of gyration, but enhances when increasing the void volume fraction. The relationship between the integrated k2-weighted SAXS intensity and the void volume fraction vf has been established theoretically for a simple two-phase system, and is given by [21]:
displayed graphically in Figure 5 as functions of the void radius of gyration. The Q values are obtained from Equation (17) in which the integral was truncated to k = 1 Ǻ−1. This choice is now obvious, because in our above discussion we have seen that this value represents the cut-off of the SAXS in a-Ge. As expected, the computed Q-factor is practically independent on the void radius of gyration, but enhances when increasing the void volume fraction. The relationship between the integrated k2-weighted SAXS intensity and the void volume fraction vf has been established theoretically for a simple two-phase system, and is given by [21]:
 (19)
(19)
In this equation V stands for the total volume and Δρ is the difference in electron density of the two phases. We have computed the second member of Equation (19) for our nanoporous models. The results are also displayed in Figure 5 for comparison. Both results are in close agreement, which supports the theoretical relation (19). The latter is often used in practice to estimate the volume fraction vf of the microstructural feature producing the SAXS. In order to go further in the quantitative analysis of the SAXS, an interesting relation coupling the invariant Q and the scattering intensity at zero-angle, I(0), has been derived theoretically for a simple two-phase system, and is given by [21]:
 (20)
(20)
Here vc is a correlation volume that measures the mean size of the heterogeneities. It is interesting to note here that this relation is independent on the volume fraction vf of the heterogeneities in the system. For nanoporous network, vc reduces to the mean volume of the nanopores and thus must scale as . Figure 5(b) shows
. Figure 5(b) shows  versus
versus  computed for all the nanoporous models listed in Table 1. A linear variation law is obvious. More interestingly, this law is independent on the void volume fraction as expected theoretically. A linear regression fit of these data has given
computed for all the nanoporous models listed in Table 1. A linear variation law is obvious. More interestingly, this law is independent on the void volume fraction as expected theoretically. A linear regression fit of these data has given 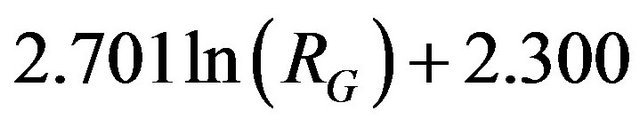 which compares favorably with the expected law
which compares favorably with the expected law
 .
.
5. Conclusion
We have presented a detailed analysis of the small-angle X-ray scattering of nanoporous atomistic models for a-Ge. The starting point was the high-quality CRN generated by Barkema and Mousseau with the improved WWW method. Widely separated nanovoids of various sizes were introduced in the preceding CRN, resulting in nanoporous models with void volume fractions that don’t exceed 6%. Each generated structure is, first, relaxed to its minimum strain energy described by the anharmonic Keating potential, then, its pair correlation function is computed, and finally, its X-ray scattering pattern is deduced. Using a Gaussians fitting procedure, the SAXS patterns are corrected for the finite size of the models, allowing so a rigorous quantitative analysis of this scattering. We have shown that at 1 Å−1 the scattering by the nanovoids is separated from that due to the atoms of the host matrix. Moreover, we confirm that the Guinier’s famous law is valid whatever the shape of the nanovoids. In addition, its k-range extends beyond the expected limit, in agreement with experimental observations. Furthermore, the invariance of the integrated SAXS intensity, on the one hand, and its relationship to the void volume fraction as well as the nanovoids size, on the other hand, are confirmed by our simulation. As a matter of fact, our present simulation is limited to relatively small and simple-shaped nanovoids, but consistent with the size of the basic CRN model. Our present work deserves to be extended to larger nanovoids with complex shapes in order to get closer to reality, but this obviously requires larger atomistic models.
6. Acknowledgements
We are indebted to Professor Normand Mousseau, of the Montréal University at Canada, for providing us its continuous random network model on which based our present study.
NOTES