Performance Analysis of Decode and Forward Cooperative Relaying over the Generalized-K Channel ()
1. Introduction
Multiple-Input Multiple-Output (MIMO) communication schemes have been widely studied to achieve diversity advantages, increased data rate, and interference suppression. However, one of the disadvantages of MIMO systems is the relatively large size needed of a wireless terminal. This is due to the requirement of an antenna spacing equal to half the wavelength to achieve sufficiently uncorrelated signals at the antenna connectors. Recently, it has been shown that cooperative diversity or user cooperation offers spatial diversity when multiple users cooperate to build a virtual antenna array [1,2], benefiting on MIMO advantages. Such a system aims to increase the channel capacity and to improve the link reliability of the wireless communications [2]. To this end, various relaying strategies have been investigated [3,4]. We distinguish mainly two techniques: Amplify and Forward (AF) (also known as analog relaying) and Decode and Forward (DF) (also known as digital relaying). In the former strategy, the relay node amplifies the received signal and then retransmits it. Thus, one disadvantage to be mentioned is the increased noise. In the latter strategy, the relay detects and possibly decodes the source message and then regenerates and retransmits it. This technique, is more reliable but it requires more processing compared to AF relaying [5]. The focus of this work is on DF relaying strategy.
To evaluate the system performance, we need to consider the propagation channel characteristics. In our context we consider the wireless channel which poses a severe challenge for reliable high-speed communication due to reflection, diffraction, scattering and absorption. To capture and model all these effects, many scientific research were carried out and they were classified mainly into three fading channel types: path-loss, multipathfading (also known as small-scale fading) and shadowing (also known as large-scale fading).
Multipath fading is relatively fast and it is, therefore, responsible for the short-term signal variations. Depending on the radio propagation environment and the underlying communication scenario, there is a range of statistical multipath fading models available in the literature, such as Rayleigh, Rician, or Nakagami-m distributions [6]. The large-scale fading (shadowing) is due to objects obstructing the propagation path as trees and buildingsgiving rise to random variations of the received power at a given distance. These fluctuations are experienced on local-mean powers. They are often modeled using a Lognormal distribution [7].
The combination of multipath fading and shadowing effects is usually known as composite fading. A versatile distribution to model the composite fading is the Generalized-K model which demonstrated a superior fit to the measured data over a wide range of physical channel conditions [8,9]. Thus, it has attracted a great deal of research interest recently. In [10], the authors have derived the outage probability, the average channel capacity and the ASEP for different modulated signals over the Generalized-K distribution. In [11], they have evaluated the spatial diversity performance over the Generalized-K channel.
Despite the multiplying number of scientific works on the cooperative diversity techniques mentioned above, most of them are limited to the Rayleigh, Rician, Lognormal and Nakagami-m channels. In [12,13], the authors studied the outage and the average error probability of adaptive DF cooperative networks with identical and non-identical Rayleigh fading channels. In [14,15] the authors derived the closed form for the outage probability of an adaptive DF over i.i.d Nakagami-m fading channels. In [16,17], the authors derived the closed form for the outage probability, the ASEP and the average channel capacity based on the MGF expression of the Nakagami-m distribution. In [18], AF cooperative diversity networks have been investigated under Generalized-K distribution. However, for a DF relaying over shadowed-Nakagami channels modeled by GeneralizedK distribution, performance analysis has never done according to our best knowledge. Recently, we have evaluated the outage probability [19], and the ASEP for M-QAM modulated signals [20], of a DF relaying technique over a Generalized-K channel. However, a complete performance analysis for different propagation environments conditions is necessary. Thus, a more detailed theoretical analysis will be presented by considering the DF relaying over the Generalized-K channel. The performance metrics under consideration are the outage probability and the ASEP. Different propagation environments will be investigated. The remainder of this paper is organized as follows. In Section 2, we introduce the system model of the DF relaying over the Generalized-K fading model. We have introduced an approximation of the Generalized-K pdf by a Gamma pdf which serves for the outage and the ASEP analysis. The closed form derivations for the outage probability and the ASEP of the non cooperative system (direct link) and the cooperative system are presented in Sections 3 and 4, respectively. Simulation results are given in Sections 5 and 6 concludes this paper.
2. System and Channel Models
2.1. Relay System Model
We consider a dual-hop cooperative wireless system consisting of 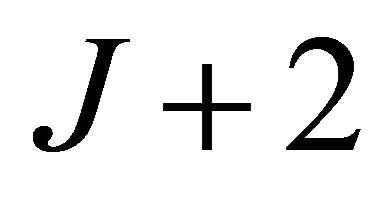 wireless nodes: one source node
wireless nodes: one source node , a set of
, a set of  relay nodes,
relay nodes,  , and a destination node
, and a destination node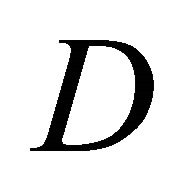 . We assume that each node has a single antenna and all
. We assume that each node has a single antenna and all  operate in half-duplex mode. We consider a time-division channel allocation scheme with
operate in half-duplex mode. We consider a time-division channel allocation scheme with 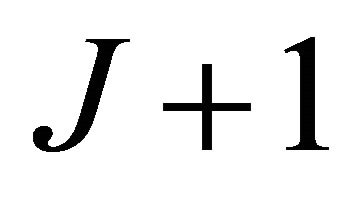 time slots. In the first time slot, the source broadcasts its message to all the nodes. During the following
time slots. In the first time slot, the source broadcasts its message to all the nodes. During the following  time slots, the source stops transmitting and the relays of the decoding set will forward the source information to the destination in a scheduled order.
time slots, the source stops transmitting and the relays of the decoding set will forward the source information to the destination in a scheduled order. 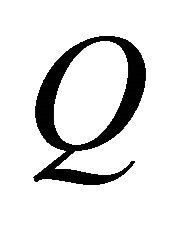 denotes the set of indexes of relays which succeed in decoding correctly the source message for a given required SNR threshold, i.e., each relay decides whether to forward the source information or not by comparing the received signal power with a decision SNR threshold. The cardinality of
denotes the set of indexes of relays which succeed in decoding correctly the source message for a given required SNR threshold, i.e., each relay decides whether to forward the source information or not by comparing the received signal power with a decision SNR threshold. The cardinality of  is denoted
is denoted . In the considered scenario, we assume that the receivers at the relays and destination have exact channel state information but no transmitter channel state information is available at the source or relays [14].
. In the considered scenario, we assume that the receivers at the relays and destination have exact channel state information but no transmitter channel state information is available at the source or relays [14].
Let us denote ,
, 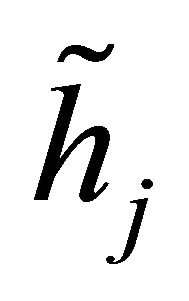 and
and 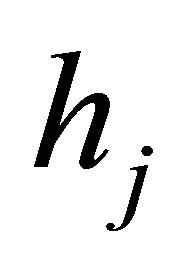 as the channel gains corresponding to the direct link, links between the source to the
as the channel gains corresponding to the direct link, links between the source to the  relay and the
relay and the  relay to the destination, respectively. Moreover,
relay to the destination, respectively. Moreover, 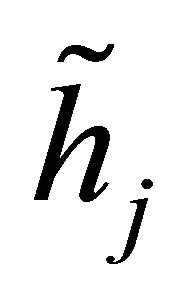 and
and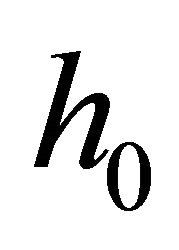 ,
, 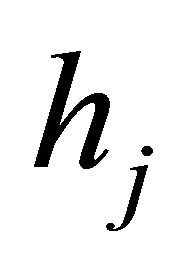 are supposed independent but not necessarily identical Generalized-K distributions with parameters
are supposed independent but not necessarily identical Generalized-K distributions with parameters ,
,  for
for 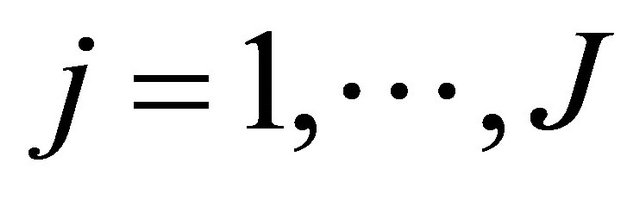 and
and ,
, 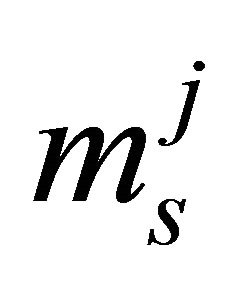 for
for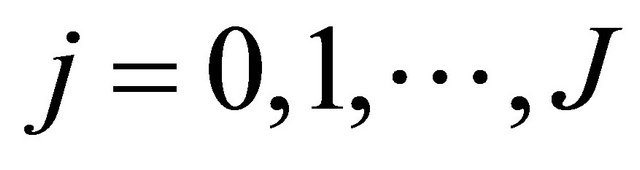 , respectively. Let
, respectively. Let  and
and  denote the instantaneous SNR received at the the
denote the instantaneous SNR received at the the  relay and the destination from the
relay and the destination from the 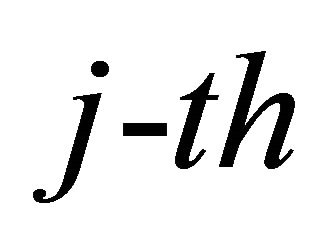 relay, respectively. Thus,
relay, respectively. Thus,
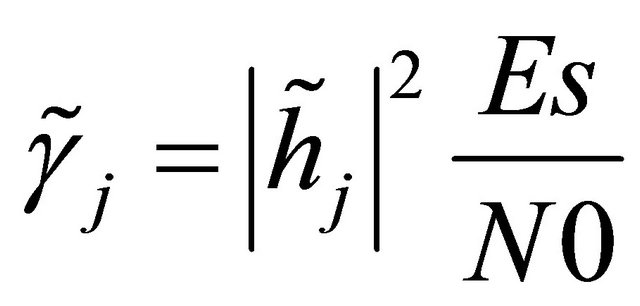 and
and 
where  is the transmit energy signal and
is the transmit energy signal and 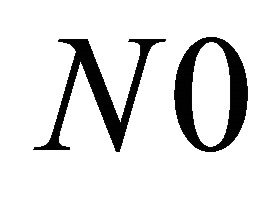 represents the single sided power spectral density of the AWGN. The corresponding average SNR are denoted
represents the single sided power spectral density of the AWGN. The corresponding average SNR are denoted
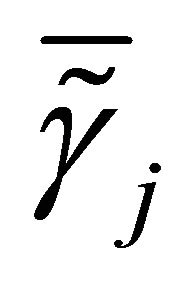 and
and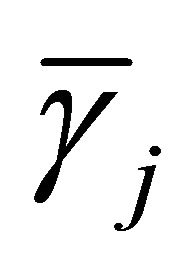 . Finally, we denote
. Finally, we denote 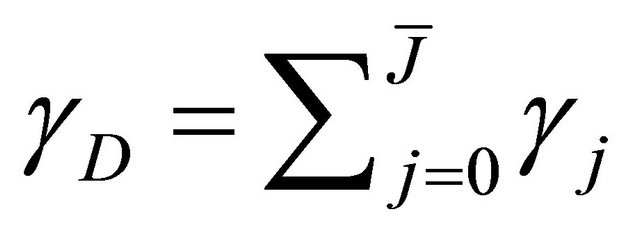 as the contribution of all the relays belonging to the set Q and the direct link using the MRC (Maximum Ratio Combiner) technique.
as the contribution of all the relays belonging to the set Q and the direct link using the MRC (Maximum Ratio Combiner) technique.
2.2. The Generalized-K Fading Channel Model
The small scale multipath fading is usually modeled using Nakagami-m distribution. The envelope of the transmitted signal over the Nakagami fading,  , has a probability density function
, has a probability density function 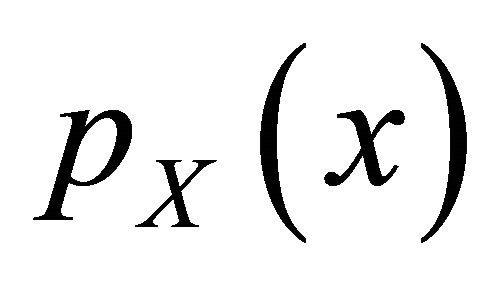 given as follows [21]
given as follows [21]
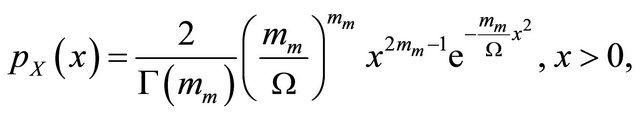 (1)
(1)
where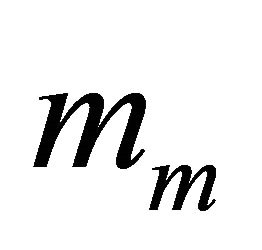 ,
,  , is the fading severity parameter called also the Nakagami parameter,
, is the fading severity parameter called also the Nakagami parameter,  ,
, 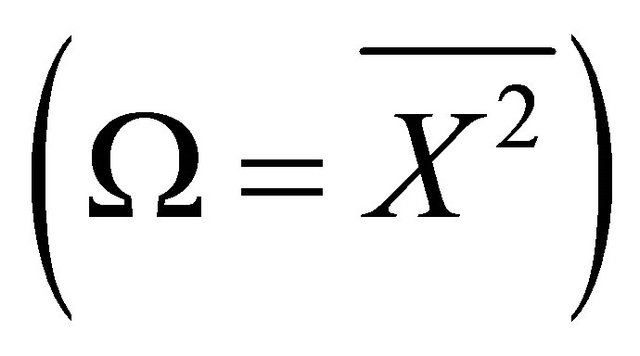 , is the average received power and
, is the average received power and 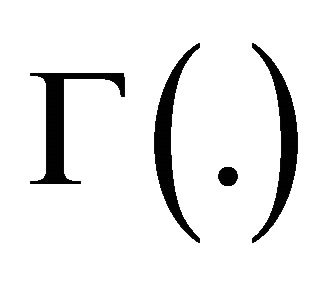 is the Gamma function.
is the Gamma function.
However, for example in terrestrial and satellite landmobile systems, the link quality is also affected by slow variation of the mean signal level due to the shadowing from terrain, buildings, and trees. Consequently, multipath fading are superimposed on shadowing. Hence, the pdf of the envelope of the received signal 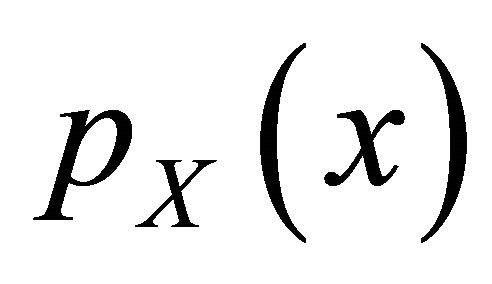 will be conditioned on the average power
will be conditioned on the average power  leading to:
leading to:
 (2)
(2)
Consequently, in combined multipath and shadowing fading, (1) can be rewritten as follows
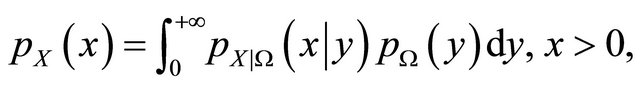 (3)
(3)
where 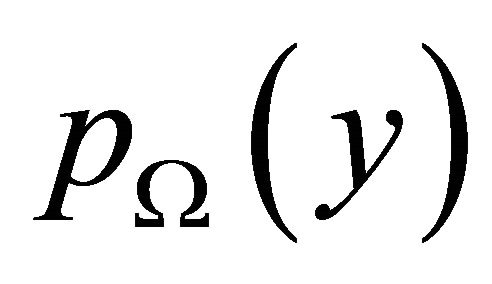 is the pdf of the average power which is usually modeled by the Lognormal distribution [21]. To mitigate difficulties to derive closed form of some metric performance measure, using the moment matching method, it has been proposed to use the Gamma distribution to model the average power random variations given as follows
is the pdf of the average power which is usually modeled by the Lognormal distribution [21]. To mitigate difficulties to derive closed form of some metric performance measure, using the moment matching method, it has been proposed to use the Gamma distribution to model the average power random variations given as follows
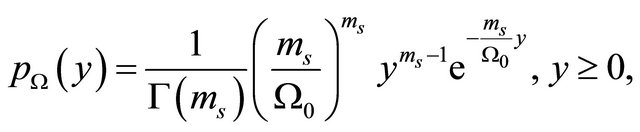 (4)
(4)
where 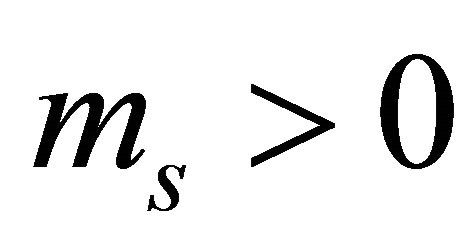 reflects the shadowing severity and
reflects the shadowing severity and 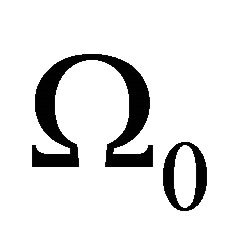 is the local mean power.
is the local mean power.
Consequently, the pdf of the received signal envelope due to the composite fading (shadowing and multipath) leads to the Generalized-K distribution which is given by
 (5)
(5)
where 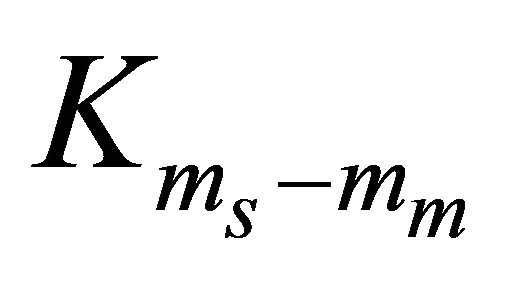 is the modified Bessel function of the second kind and order
is the modified Bessel function of the second kind and order 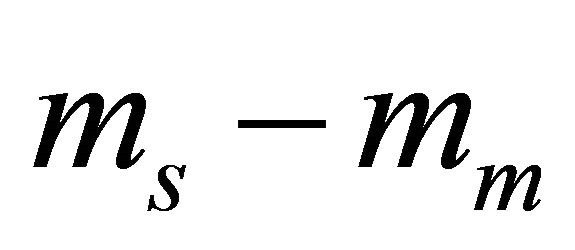 and
and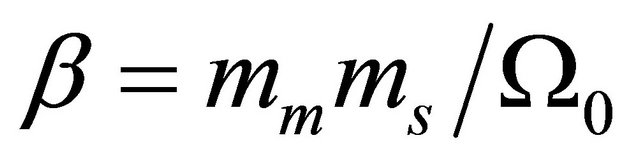 .
.
In the cooperative system, as mentioned in [2], to capture the path-loss effects, we use
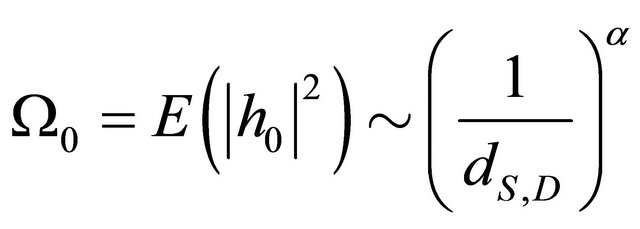 ,
, 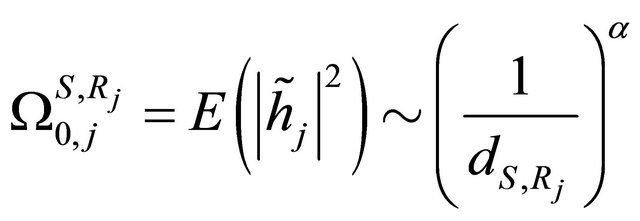 ,
, 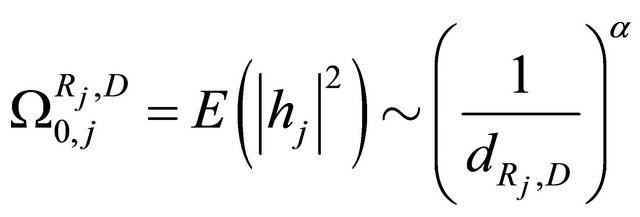 where
where 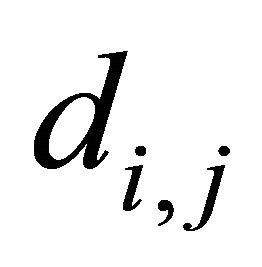 is the distance between the terminals
is the distance between the terminals  and
and , and
, and  is the pathloss exponent.
is the pathloss exponent.
Over a Generalized-K fading channel the pdf of the output instantaneous SNR 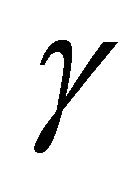 follows a Generalized-K distribution given by [11]
follows a Generalized-K distribution given by [11]
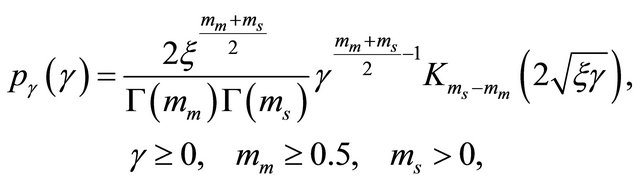 (6)
(6)
where 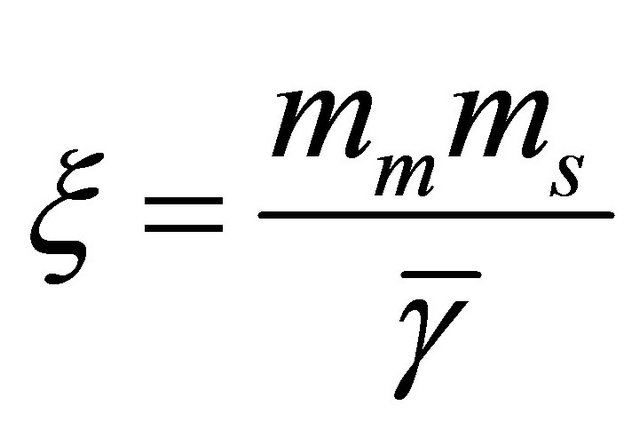 and
and 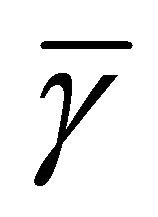 is the average SNR over the considered channel.
is the average SNR over the considered channel.
In the next section, we deal with the outage probability and the ASEP closed form derivations. To this end, in the cooperative case, we deal with the cdf of the sum of 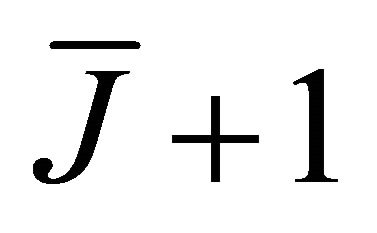 Generalized-K random variables. As pointed in [22,23], the computation of the cdf expression is not straightforward and requires the use of approximations and asymptotic expansions or the use of the numerical inversion of the characteristic function. An alternative approach, to avoid the analytical difficulties, is to consider an approximation of the Generalized-K pdf, given by (6), using the moment matching method by a more tractable pdf [22], as shown in the next subsection.
Generalized-K random variables. As pointed in [22,23], the computation of the cdf expression is not straightforward and requires the use of approximations and asymptotic expansions or the use of the numerical inversion of the characteristic function. An alternative approach, to avoid the analytical difficulties, is to consider an approximation of the Generalized-K pdf, given by (6), using the moment matching method by a more tractable pdf [22], as shown in the next subsection.
2.3. The Approximation of a Generalized-K pdf
The main goal of this subsection is to give the analytical and main results of the approximation of the Generalized-K pdf by a suitable Gamma pdf. This approximation has been developed in two steps [22]:
• Approximation of the Generalized-K pdf by a Gamma pdf by matching the two first positive moments.
• Introduction of an adjustment factor for the shape and the scale parameters of the approximating Gamma pdf.
If we consider the distribution given by (5), the 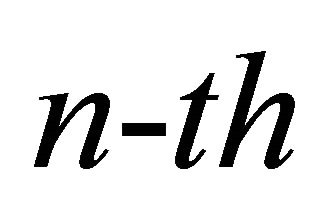 moment of the Generalized-K distribution can be derived as [22]
moment of the Generalized-K distribution can be derived as [22]
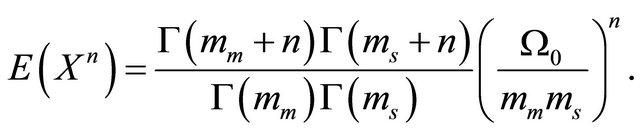 (7)
(7)
The 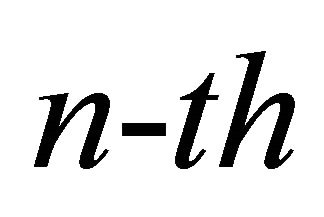 moment of the approximating Gamma distribution can be expressed as
moment of the approximating Gamma distribution can be expressed as
 (8)
(8)
where  and
and 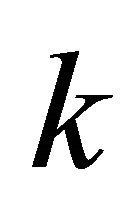 denote the scale and shape parameters of the approximating Gamma distribution, respectively.
denote the scale and shape parameters of the approximating Gamma distribution, respectively.
Matching the two first positive moments of the Generalized-K distribution to those of the approximating Gamma distribution results in
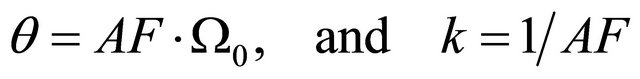 (9)
(9)
where  is the amount of fading in the composite fading channel and
is the amount of fading in the composite fading channel and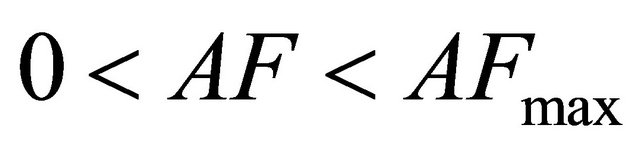 ,
, 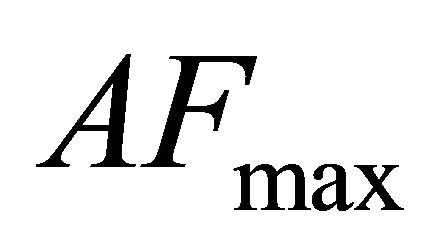 is determined by the smallest physical values of
is determined by the smallest physical values of  and
and . However, this approximation results in a poor fitting in the lower and upper tail regions as compared to the original pdf. In order to bypass this inaccuracy, an adjustable form has been introduced for the scale and shape parameters of the region-wise approximating Gamma pdf for the two first moments. These parameters are given as follows
. However, this approximation results in a poor fitting in the lower and upper tail regions as compared to the original pdf. In order to bypass this inaccuracy, an adjustable form has been introduced for the scale and shape parameters of the region-wise approximating Gamma pdf for the two first moments. These parameters are given as follows
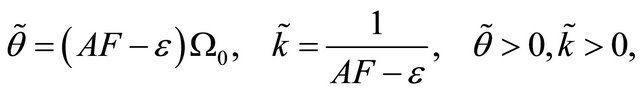 (10)
(10)
where the adjustment parameter 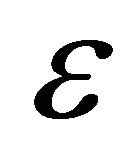 is chosen so that the pdf (cdf) of the approximating Gamma distribution becomes as close as desired to the pdf (cdf) of the Generalized-K distribution in a certain region of interest. We note that
is chosen so that the pdf (cdf) of the approximating Gamma distribution becomes as close as desired to the pdf (cdf) of the Generalized-K distribution in a certain region of interest. We note that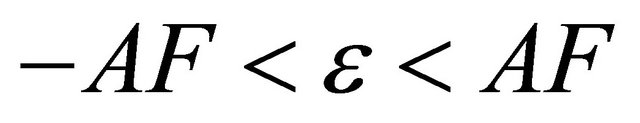 . Since, the relevant practical range of AF is from zero (for non-fading channels) to 8 (for severe multipath fading and shadowing conditions corresponding to
. Since, the relevant practical range of AF is from zero (for non-fading channels) to 8 (for severe multipath fading and shadowing conditions corresponding to 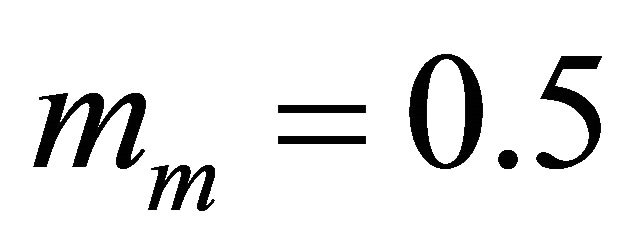 and
and ), the relevant range of the adjustment factor is
), the relevant range of the adjustment factor is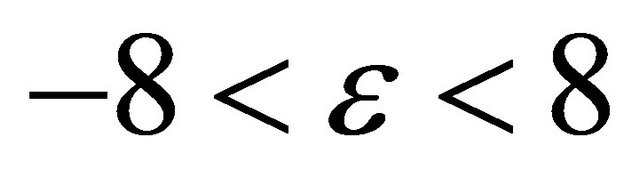 .
.
2.4. Approximation of the pdf of the Sum of N Independent Generalized-K Random Variables
As aforementioned in Subsection 2.3, the pdf of the sum of N Generalized-K random variables can be approximated by a Gamma pdf using the adjustable form.
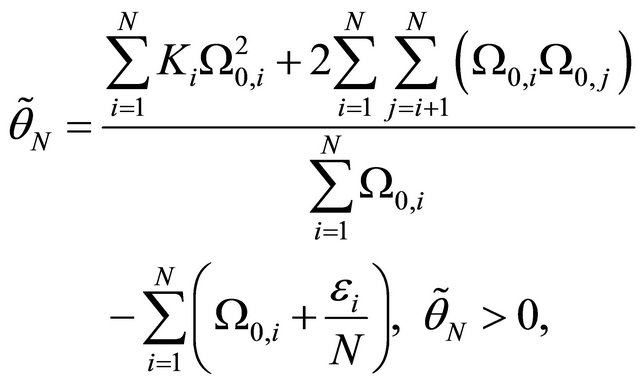 (11)
(11)
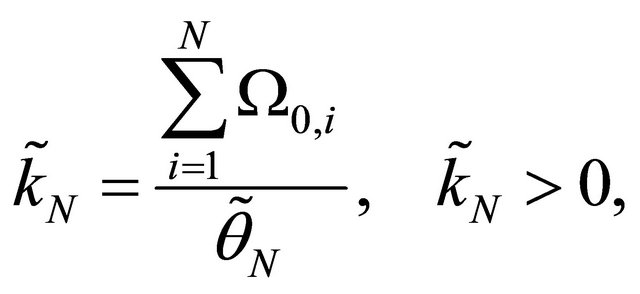 (12)
(12)
where .
.  and
and  are the shape parameters of the
are the shape parameters of the 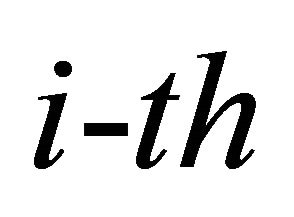 Generalized-K random variable.
Generalized-K random variable.
We note that for the i.i.d case, the expressions in (11) and (12) simplify to
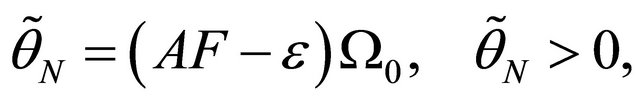 (13)
(13)
 (14)
(14)
An illustration of the choice of the optimal value of the adjustment factor is given in Section 5.
3. Performance of the Non Cooperative System (Direct Link)
In the following, we consider the outage probability and the ASEP as performance system metrics.
3.1. Outage Probability
The outage probability represents the probability of unsatisfactory signal reception. It can be defined as the probability that the received SNR is less than a specified SNR threshold value at the destination, denoted 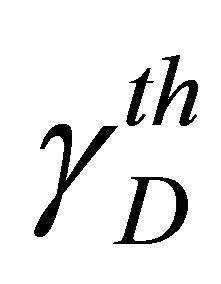 [10]. We consider the direct link composed by the source and the destination node communicating over the composite fading channel. The outage probability denoted
[10]. We consider the direct link composed by the source and the destination node communicating over the composite fading channel. The outage probability denoted 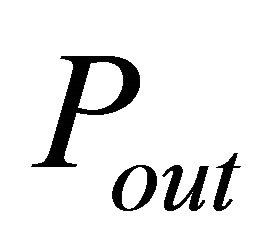 is given as [10]
is given as [10]
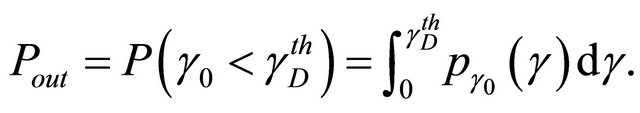 (15)
(15)
We note that 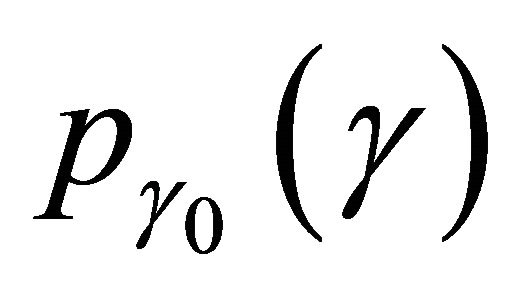 is given by (6). According to [10], we can derive
is given by (6). According to [10], we can derive 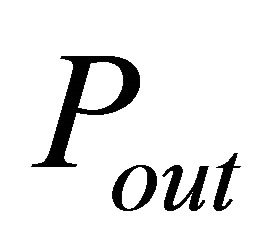 as follows
as follows
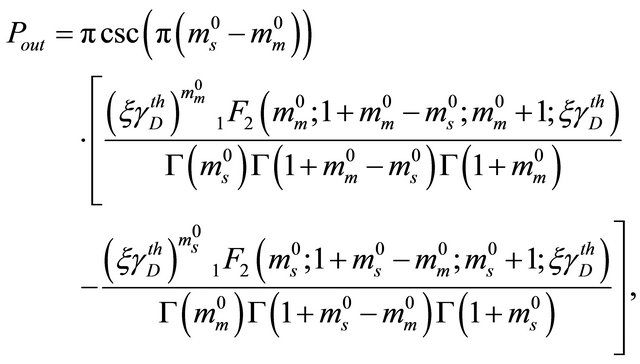 (16)
(16)
where ,
,  is the cosecant function, and
is the cosecant function, and
 is the generalized hyper-geometric function
is the generalized hyper-geometric function
[24].
3.2. Average Symbol Error Probability
The ASEP, 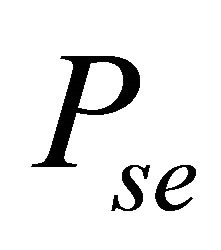 , for modulated signals over the fading channel
, for modulated signals over the fading channel 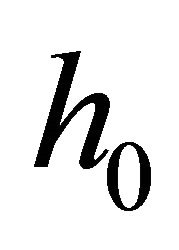 can be obtained by averaging its conditional symbol error probability,
can be obtained by averaging its conditional symbol error probability, 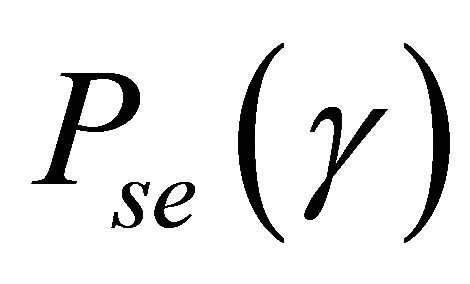 , under a given SNR
, under a given SNR 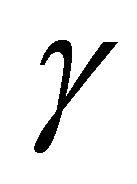 in AWGN over the pdf of the received SNR
in AWGN over the pdf of the received SNR 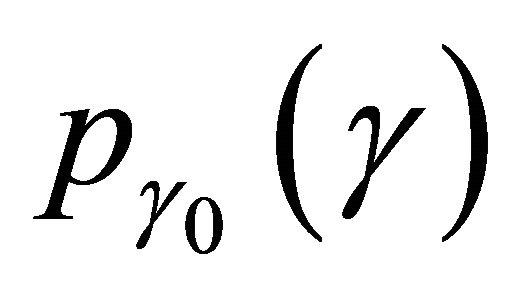
 (17)
(17)
In this paper, we consider M-QAM modulated signals over Generalized-K fading channel. Thus, 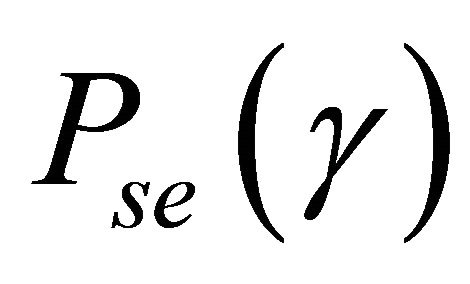 can be expressed as
can be expressed as 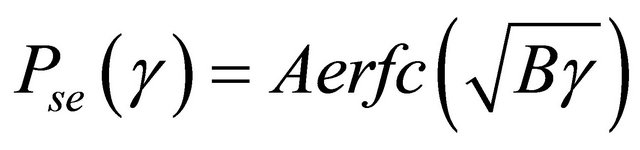 [6], where
[6], where
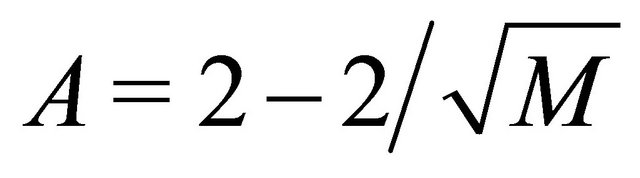 ,
, 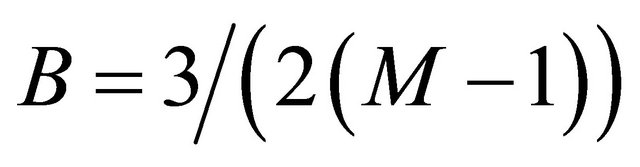 and
and
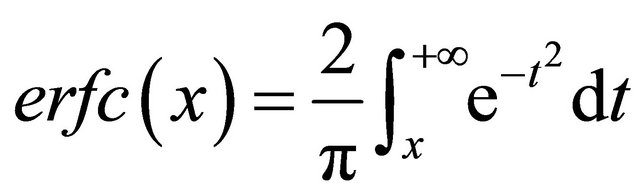 . By considering the same notations above, the closed form of the ASEP for the direct link is given by [10].
. By considering the same notations above, the closed form of the ASEP for the direct link is given by [10].
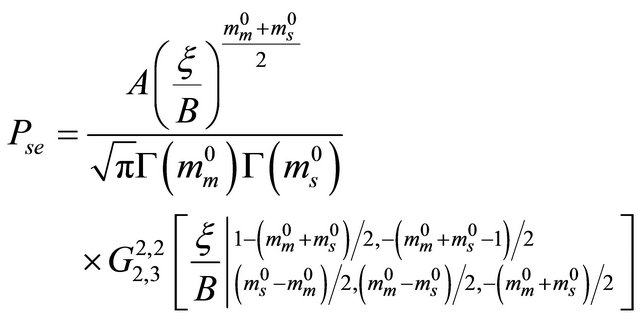 (18)
(18)
where , is the Meijer’s G-function [24].
, is the Meijer’s G-function [24].
4. Performance of the Cooperative System
4.1. Outage Probability
In the cooperative case, the outage probability 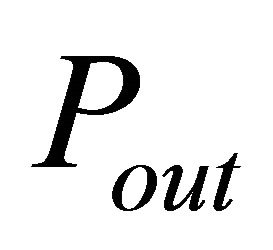 is obtained by the contribution of all the relay nodes belonging to the set Q and the direct link using the MRC (Maximum Ratio Combining) technique. Thus, by using the law of total probability we obtain
is obtained by the contribution of all the relay nodes belonging to the set Q and the direct link using the MRC (Maximum Ratio Combining) technique. Thus, by using the law of total probability we obtain
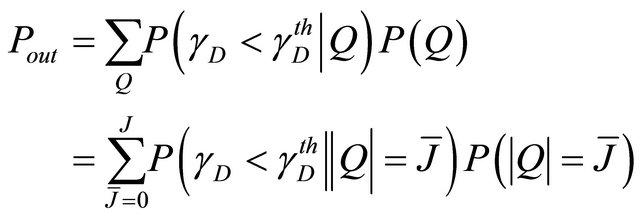 (19)
(19)
where  is the probability that
is the probability that  nodes cooperate in relaying information to the destination.
nodes cooperate in relaying information to the destination.
 is the conditional outage probability in the case of
is the conditional outage probability in the case of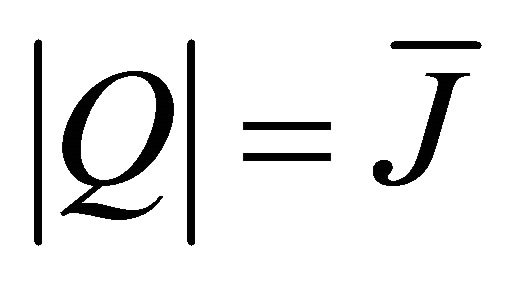 . In the following, we shall derive the expression of
. In the following, we shall derive the expression of 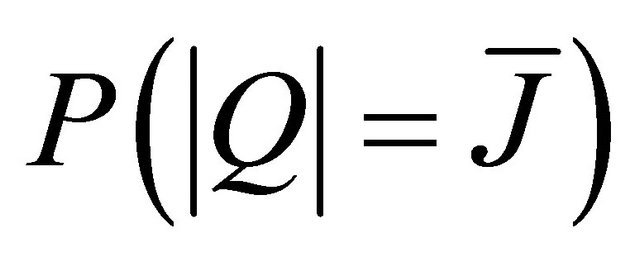 and
and
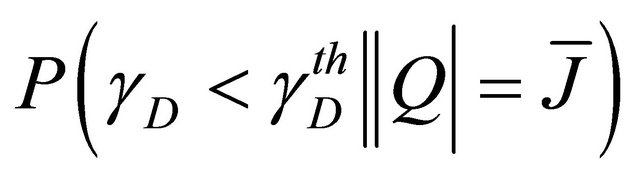 , respectively.
, respectively.
a) Calculation of 
The probability that the 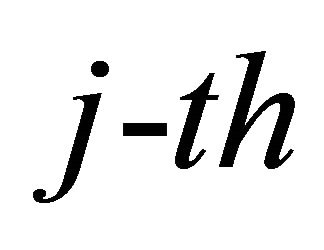 relay-node is in the decoding set
relay-node is in the decoding set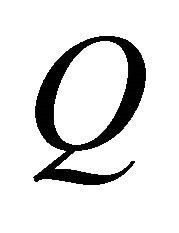 , is defined as the probability that its SNR,
, is defined as the probability that its SNR,  , is larger than the threshold SNR at the
, is larger than the threshold SNR at the  relay,
relay, . It is given as follows
. It is given as follows
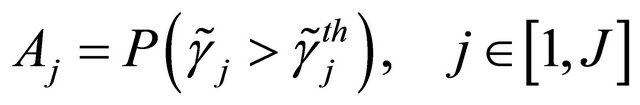 (20)
(20)
For simplicity, we choose the same threshold for all the relays, i.e,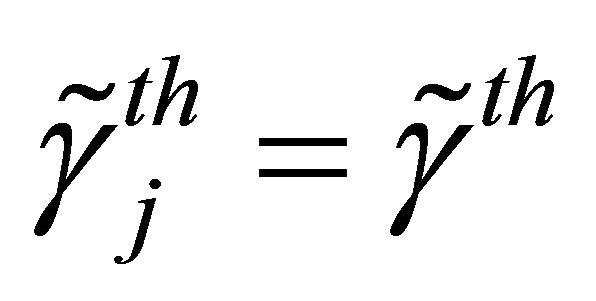 .
.
Consequently, 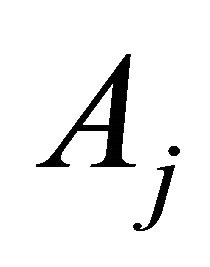 is given as follows
is given as follows
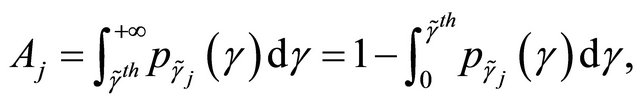 (21)
(21)
where 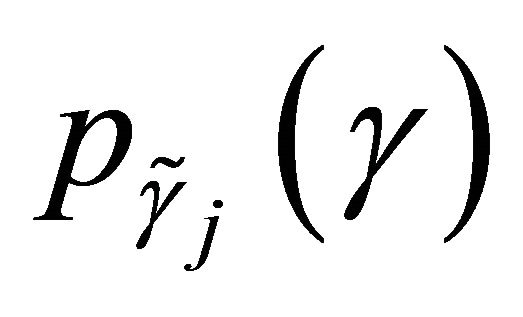 is the probability density of the SNR at the
is the probability density of the SNR at the 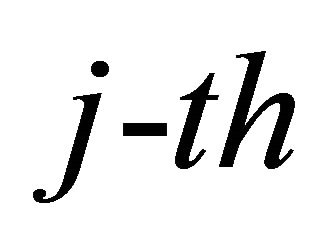 relay. It is given by (6) and its cdf function is given by (16) by setting
relay. It is given by (6) and its cdf function is given by (16) by setting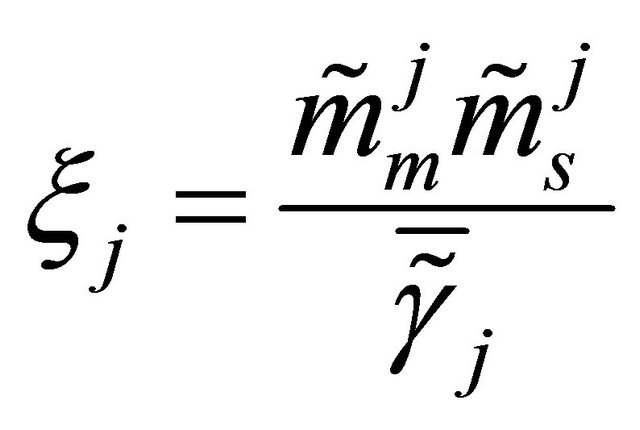 . Thus,
. Thus, 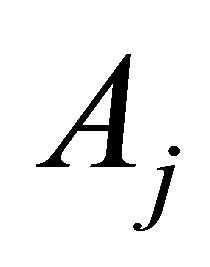 is deduced easily.
is deduced easily.
Let 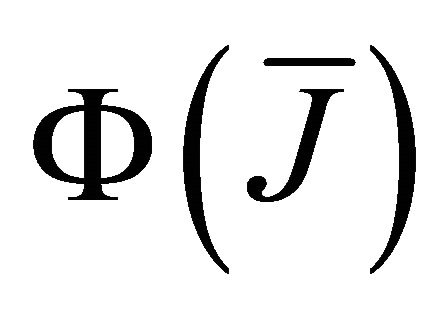 denotes a combination that
denotes a combination that  of
of  nodes cooperate in relaying information to the destination and
nodes cooperate in relaying information to the destination and 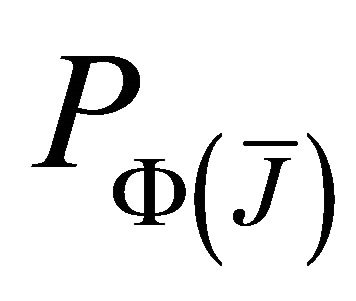 as the corresponding probability. Assuming that the relay channels are independent,
as the corresponding probability. Assuming that the relay channels are independent,  can be expressed as
can be expressed as
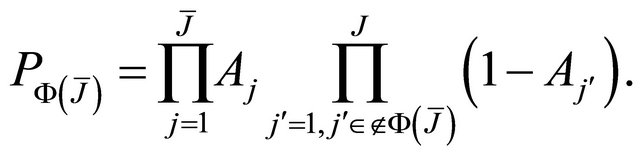 (22)
(22)
Consequently,
 (23)
(23)
b) Calculation of 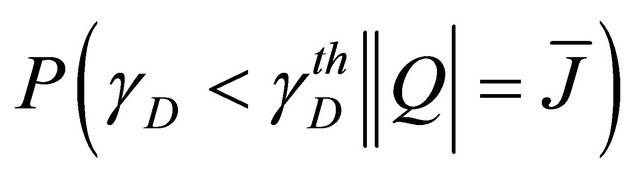
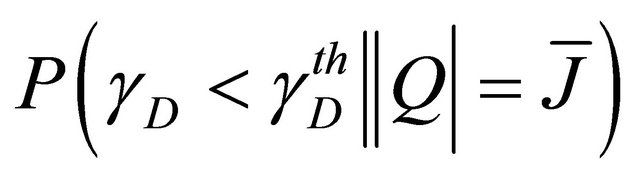 can be seen as the cdf of
can be seen as the cdf of
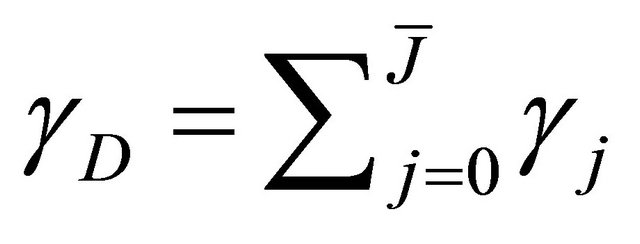 , evaluated at
, evaluated at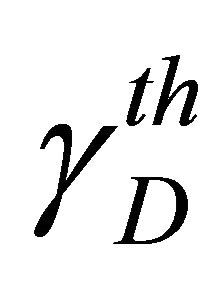 , i.e. the sum of the
, i.e. the sum of the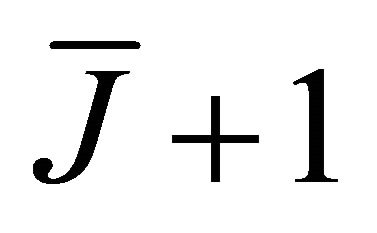 .
.
Generalized-K random variables correspond to the 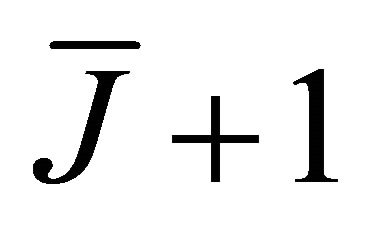 active links. As mentioned above in Section 2.4, to avoid analytical complexity, the computation of the cdf expression of
active links. As mentioned above in Section 2.4, to avoid analytical complexity, the computation of the cdf expression of  can be approximated by the Gamma pdf with the scale and shape parameters given by (11) and (12), respectively. Consequently,
can be approximated by the Gamma pdf with the scale and shape parameters given by (11) and (12), respectively. Consequently, 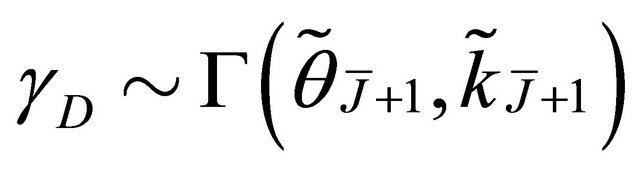 and it is expressed as
and it is expressed as
 (24)
(24)
where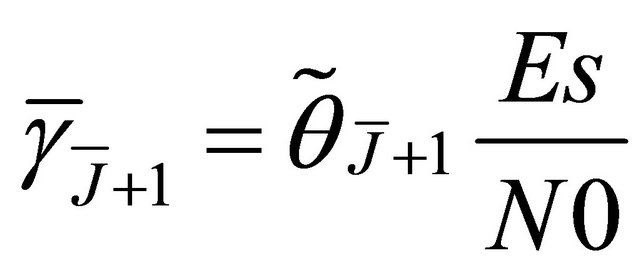 .
.
Consequently 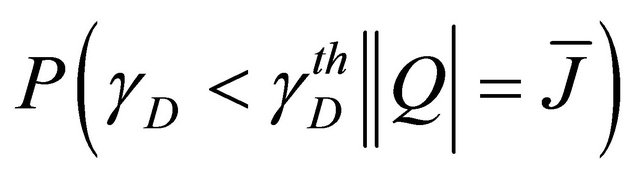 is given as follows
is given as follows
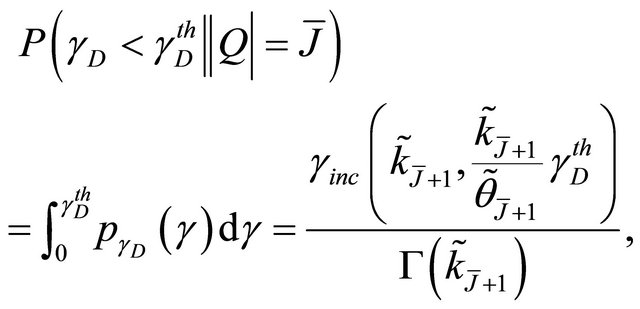 (25)
(25)
where  is the incomplete Gamma function. Finally, from (21)-(23) and (25) we derive the outage probability at the destination for the cooperative system as
is the incomplete Gamma function. Finally, from (21)-(23) and (25) we derive the outage probability at the destination for the cooperative system as
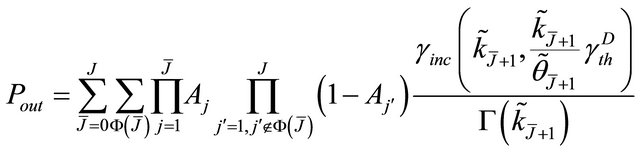 (26)
(26)
4.2. Average Symbol Error Probability
In the cooperative case, the ASEP 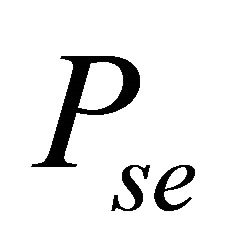 is obtained by the contribution of all the relay nodes and the direct link. At the MRC output, by considering the same notation as above,
is obtained by the contribution of all the relay nodes and the direct link. At the MRC output, by considering the same notation as above, 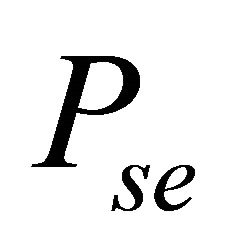 can be expressed as follows
can be expressed as follows
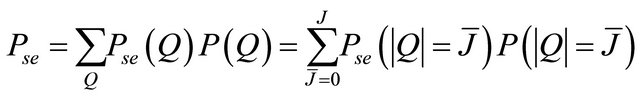 (27)
(27)
 has been calculated in the last subsection given by (23).
has been calculated in the last subsection given by (23). 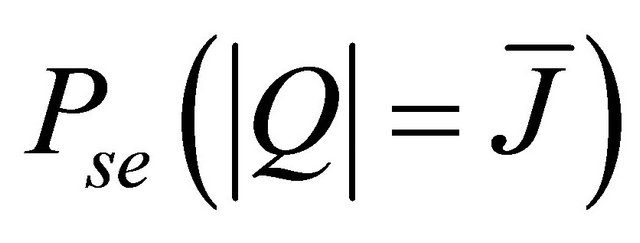 is the conditional symbol error probability corresponding to the cooperation of the
is the conditional symbol error probability corresponding to the cooperation of the  branches and the direct link (source-destination). In the following, we shall derive its expression.
branches and the direct link (source-destination). In the following, we shall derive its expression.
a) Calculation of 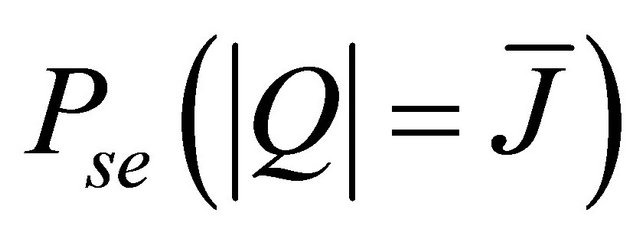
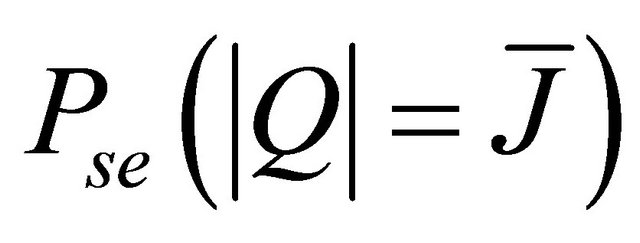 can be seen as the probability of occurring an error when
can be seen as the probability of occurring an error when  relays are active. As mentioned in the last section, it can be expressed as
relays are active. As mentioned in the last section, it can be expressed as
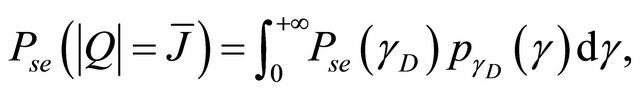 (28)
(28)
where 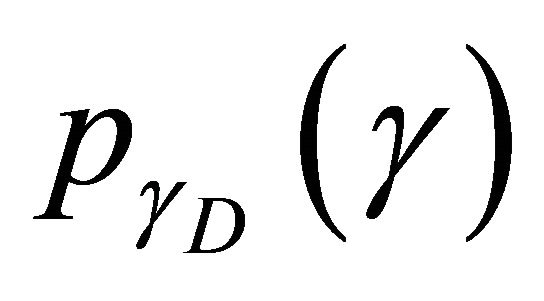 is given by (24) and
is given by (24) and  is expressed as
is expressed as
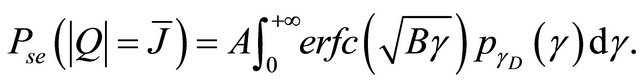 (29)
(29)
To evaluate this integral, we use the relationship
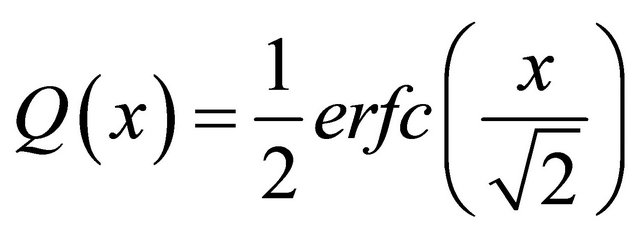 which leads to a new integral form as follows
which leads to a new integral form as follows
 (30)
(30)
where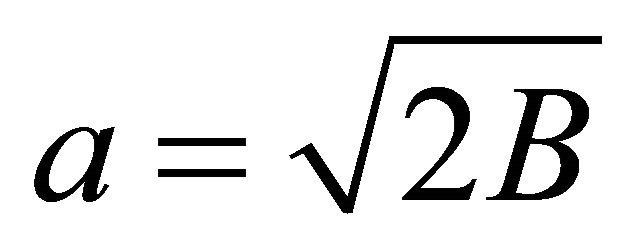 . Using ([6], (5.1), (5.18)), this integral is deduced as follows.
. Using ([6], (5.1), (5.18)), this integral is deduced as follows.
For integer values of ,
,  can be written as
can be written as
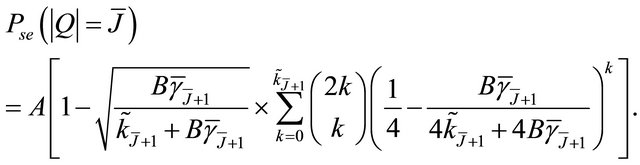 (31)
(31)
For non-integer values of ,
, 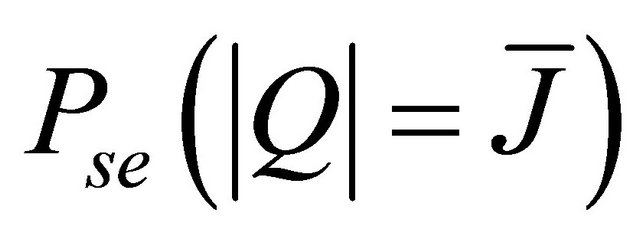 can be written as
can be written as
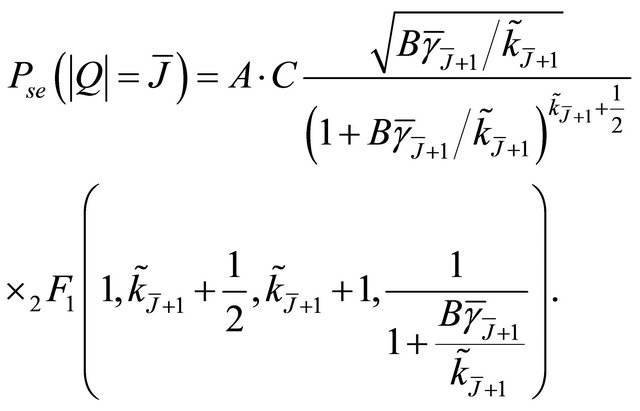 (32)
(32)
where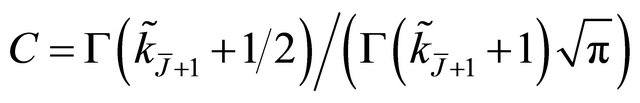 .
.
Thus, using (23), (27), (31) or (32), the ASEP 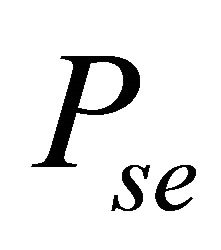 can be deduced easily.
can be deduced easily.
5. Simulation Results
In this section, we present Monte-Carlo simulations to illustrate the previous theoretical results for both the outage probability and the ASEP.
5.1. Outage Probability
To be more accurate in our illustrations, we have simulated the shadowed Nakagami channel by taking into account the Nakagami-m distribution and the Log-normal distribution. For the non cooperative system, Figure 1 depicts the outage probability versus the threshold SNR, 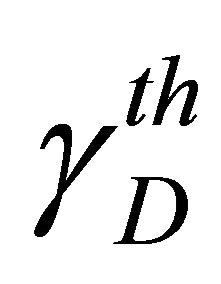 , for a transmit SNR of
, for a transmit SNR of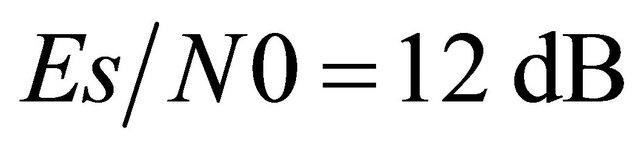 . The Threshold SNR at the relays is chosen
. The Threshold SNR at the relays is chosen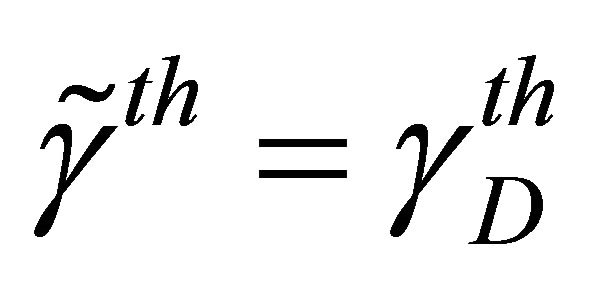 . We have considered three different environments with increasing propagation hardness:
. We have considered three different environments with increasing propagation hardness:
• Generalized-K channel with 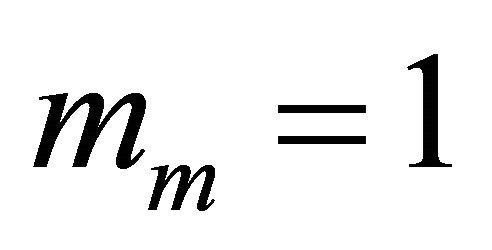 and
and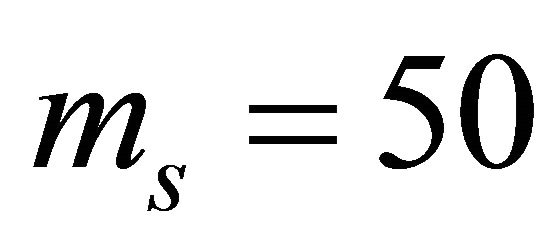 : for high values of
: for high values of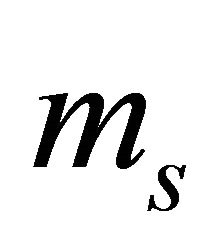 , greater than
, greater than , we consider that there is no shadowing. It is equivalent to Rayleigh channel. The corresponding plots in Figure 1, show less outage probability compared to the others configurations. Moreover, they are close each other. We note the robustness of the channel simulation compared to the theoretical rayleigh performance. Besides, we deduce the accuracy of the approximated model compared to the exact formula;
, we consider that there is no shadowing. It is equivalent to Rayleigh channel. The corresponding plots in Figure 1, show less outage probability compared to the others configurations. Moreover, they are close each other. We note the robustness of the channel simulation compared to the theoretical rayleigh performance. Besides, we deduce the accuracy of the approximated model compared to the exact formula;
• Generalized-K channel with 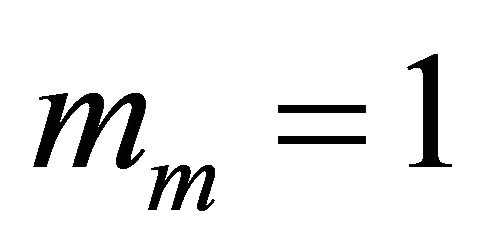 and
and ;
;
• Generalized-K channel with 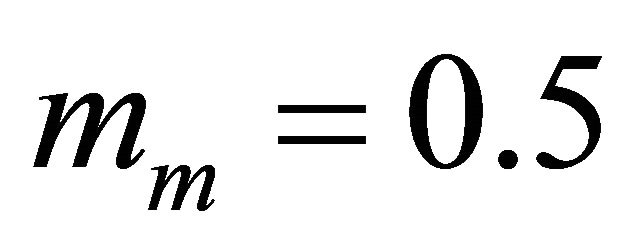 and
and .
.
For the two last configurations, we note similar performances between the Generalized-K cdf and the approximated Gamma cdf with an optimal value of  for
for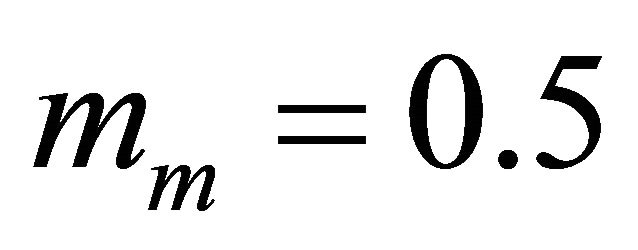 , and
, and 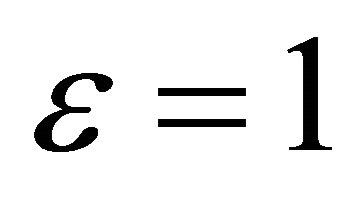 for
for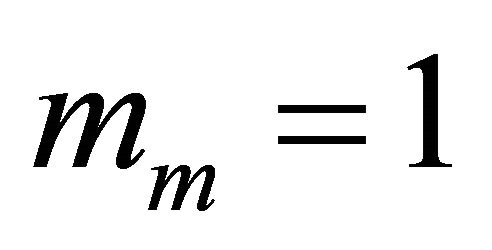 . More precisely, the optimal value of
. More precisely, the optimal value of 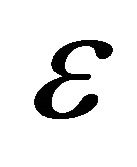 is obtained for lower tail approximation, since we are interested in small threshold values. We note just a small difference between theoretical results and simulation which is due to the approximation of the Log-normal pdf distribution by a Gamma distribution to model the shadowing fading.
is obtained for lower tail approximation, since we are interested in small threshold values. We note just a small difference between theoretical results and simulation which is due to the approximation of the Log-normal pdf distribution by a Gamma distribution to model the shadowing fading.
In some cases, it is important to illustrate the outage
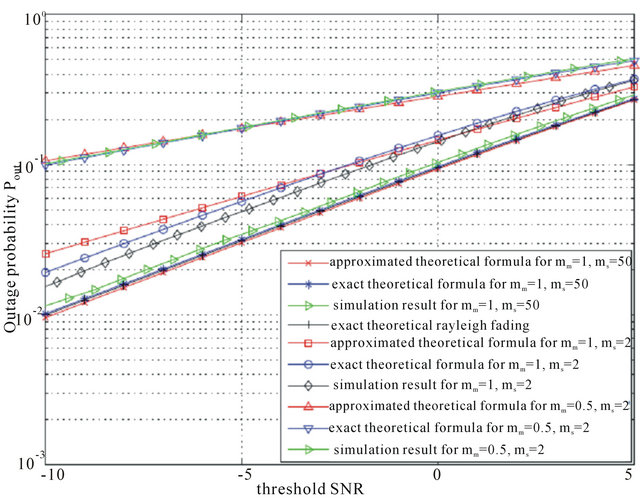
Figure 1. Outage probability versus the threshold SNR 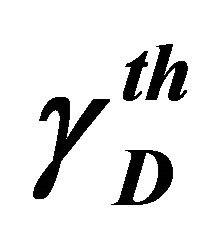 for the non cooperative system.
for the non cooperative system.
probability measure as function of the average SNR for a given threshold SNR. Figure 2 shows this illustration for 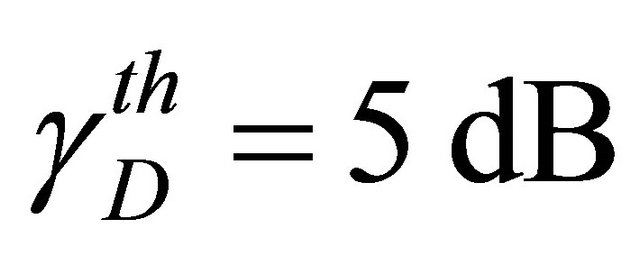 for the same parameters of the three configurations mentioned above.
for the same parameters of the three configurations mentioned above.
In the cooperative communication scenario, we have omitted the propagation environment relative to Rayleigh case; we have considered the two others environments cases corresponding to 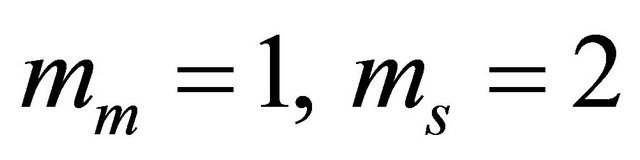 and
and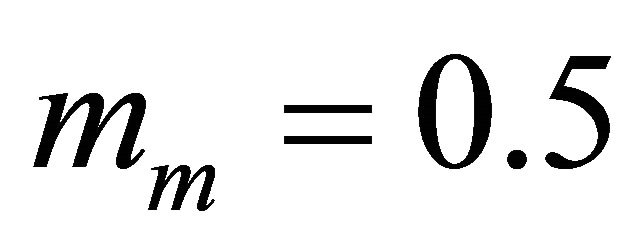 ,
, 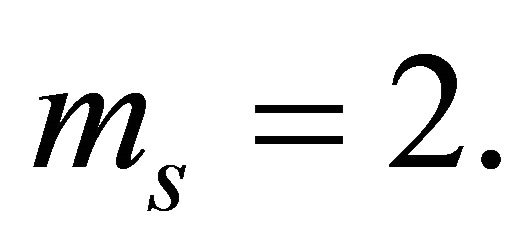 For both cases, we have considered identical Nakagami-m shadowed fading channels for the links of the first hop and those of the second dual hop.
For both cases, we have considered identical Nakagami-m shadowed fading channels for the links of the first hop and those of the second dual hop.
We have considered a number of relay nodes, J = 1, 2, and 3. Similarly to the non cooperative system, we have illustrated:
• The outage probability versus the threshold SNR 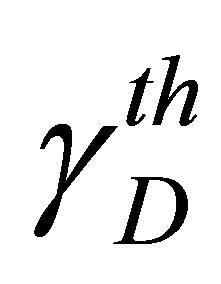 for a transmit SNR value of
for a transmit SNR value of  for both the first and the second hops. Figures 3 and 4 show
for both the first and the second hops. Figures 3 and 4 show
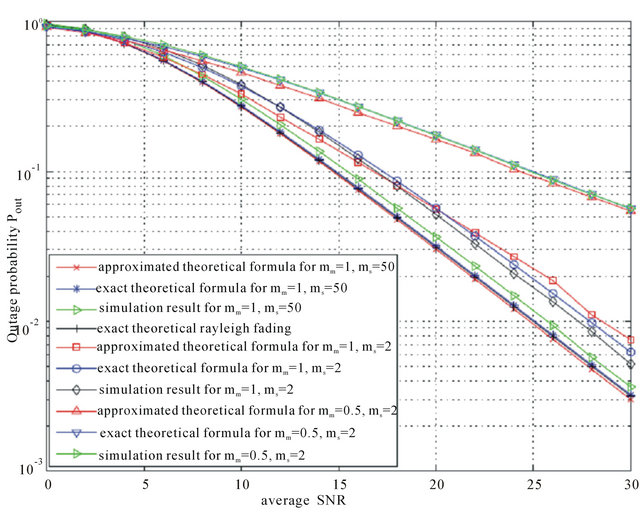
Figure 2. Outage probability versus 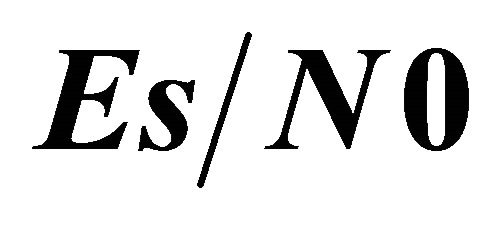 for the non cooperative system.
for the non cooperative system.
the obtained results.
• The outage probability versus 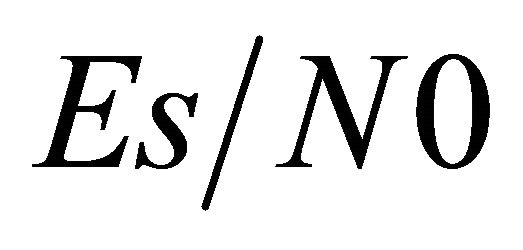 for a given threshold SNR
for a given threshold SNR . Figures 5 and 6 show the obtained results.
. Figures 5 and 6 show the obtained results.
We note that, since we consider i.i.d channels, the optimal value of 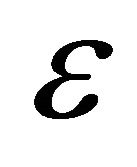 is the same for all links, as mentioned in the theoretical analysis. Thus,
is the same for all links, as mentioned in the theoretical analysis. Thus, 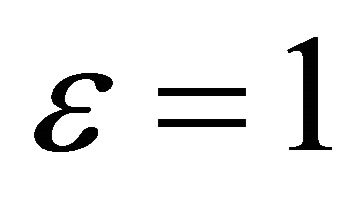 for mm = 1,
for mm = 1,  and
and 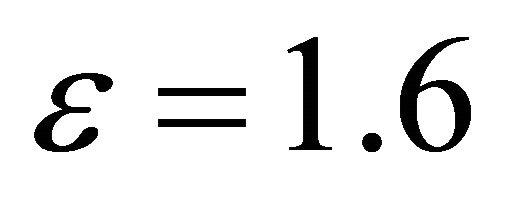 for
for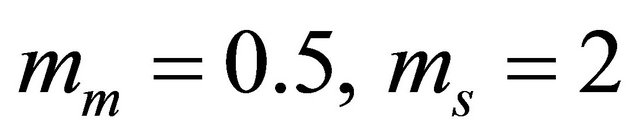 . We observe that theoretical results match well simulation results. The little difference is again due to the approximation of the Log-normal distribution by a Gamma distribution. As expected, the use of more relays provides better outage performance.
. We observe that theoretical results match well simulation results. The little difference is again due to the approximation of the Log-normal distribution by a Gamma distribution. As expected, the use of more relays provides better outage performance.
5.2. Average Symbol Error Probability
In this subsection, we have illustrated the results relative
to the ASEP for 16-QAM modulated signals. We plot the performance curves in terms of the analytical and simulation ASEP versus 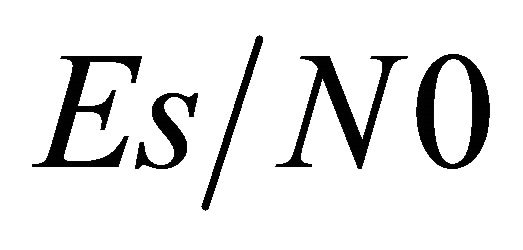 in dB. Similarly to the outage analysis, we consider two scenarii: the non cooperative and the cooperative systems. Figure 7 shows the obtained results for the first scenario.
in dB. Similarly to the outage analysis, we consider two scenarii: the non cooperative and the cooperative systems. Figure 7 shows the obtained results for the first scenario.
We note a similar performance between the theoretical Rayleigh curve, the approximated results and the simulation results.
For the second scenario, we have considered identical and independent channels with the following parameters  and
and . We have considered a threshold SNR
. We have considered a threshold SNR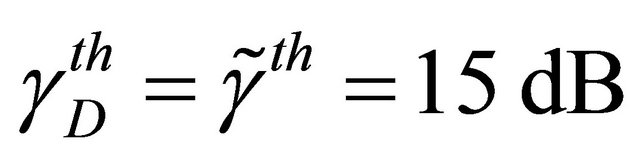 . To capture the path-loss effects, we have considered the following distances
. To capture the path-loss effects, we have considered the following distances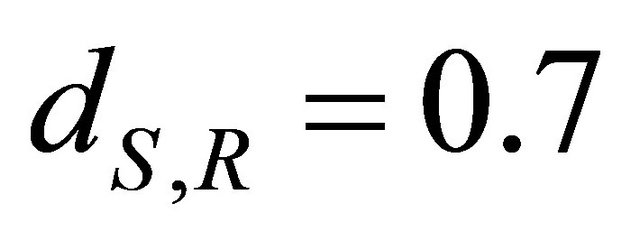 ,
, 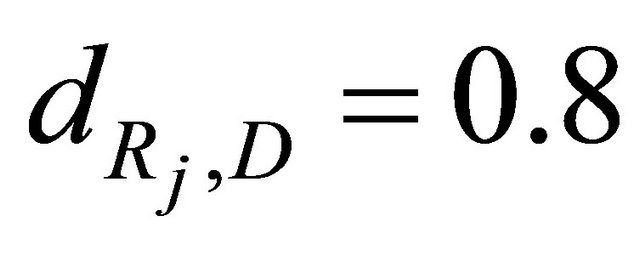 and
and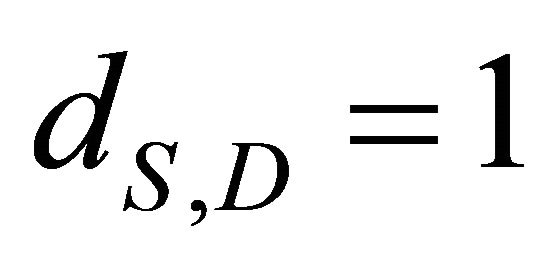 . We have chosen a number of relay nodes, J = 1, 2, and 3. Obtained results are depicted in Figure 8. Optimal values of
. We have chosen a number of relay nodes, J = 1, 2, and 3. Obtained results are depicted in Figure 8. Optimal values of  are calculated for each
are calculated for each 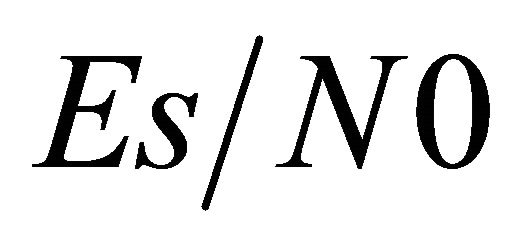 value. They are given by Table 1.
value. They are given by Table 1.
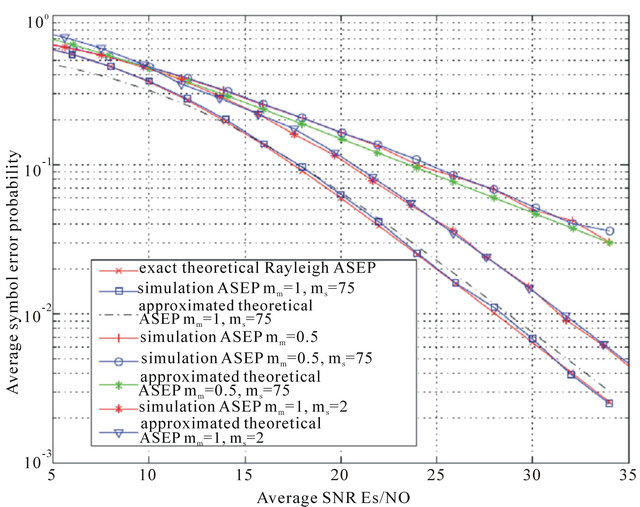
Figure 7. Average symbol error probability versus  for the non cooperative system.
for the non cooperative system.
Table 1. 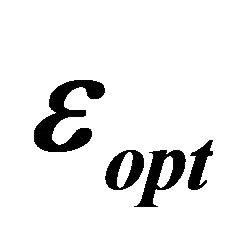 versus
versus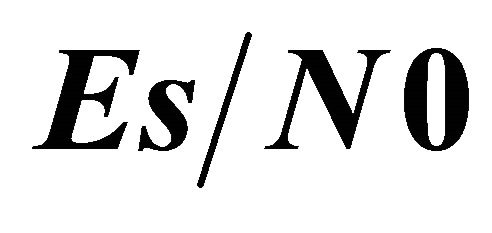 .
.

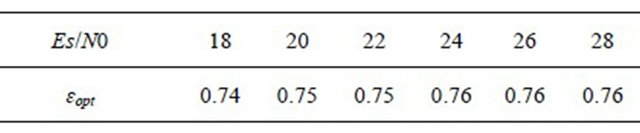
We note a good match between the simulation and theoretical results. The small difference between theoretical results and simulation includes the combination of the two approximations: approximation of the Lognormal pdf distribution by a Gamma distribution and the approximation of the Generalized-K distribution by a Gamma distribution. As expected, the use of more relays provides better ASEP performance.
6. Conclusion
We have analyzed the outage probability and the ASEP of an adaptive DF relaying over the composite fading multipath/shadowing channels modeled by a Generalized-K distribution. The utilization of an approximation of the Generalized-K pdf by an adjustable form of a Gamma distribution based on the two first moments matching method has been presented and validated by simulation under severe fading conditions. Based on this approximation, we derived closed-form expressions for the outage probability and the ASEP. We have provided Monte-Carlo simulations which are in good agreement with our theoretical analysis. This solution is helpful to investigate the performance analysis of cooperative networks under different environment conditions.