A Study of Super Nonlinear Motion of Electrostatically Coupled Two-Particle System ()
1. Introduction
In search of realistic, practical, nonlinear physics phenomena in our previous work we envision a coupled two-particle system [1,2]. In short, we consider a system composed of a pair of mechanical, electrically charged pendulums with a common pivot allowing oscillations in a vertical plane. The design of the system allows an adaptive investigation of the nonlinear oscillations. The mutual electrostatic interaction of the charged pendulums, irrespective the oscillation amplitudes make the oscillations nonlinear by itself. To make the analysis somewhat general, we consider large amplitude oscillations resulting from gravity pull and electrostatic interaction; appropriately we called the system “super nonlinear oscillations”. For sake of transparency, however, we assume identical pendulums. Meaning, we assign the same parameters to each pendulum, such as {{,m,q}. Furthermore, we apply the same initial conditions such as the initial swing angles and velocities,  to both pendulums. Under these conditions, intuitively, it is plausible to conclude the pendulums are to oscillate coherently. And each pendulum is to trace a repeatable trajectory in time. And indeed we were able quantitatively confirm our intuitive predictions.
to both pendulums. Under these conditions, intuitively, it is plausible to conclude the pendulums are to oscillate coherently. And each pendulum is to trace a repeatable trajectory in time. And indeed we were able quantitatively confirm our intuitive predictions.
To generalize the analysis, in our current work we relax the aforementioned restrictions; we consider two nonidentical pendulums. We also select nonidentical initial conditions. Under these conditions, softly speaking, our intuition is not strong enough to predict and envision the motion of the individual pendulum.
We show, these asymmetries result unpredictable, nonrepeatable chaotic motions in time. Each pendulum under the influence of the Coulombian electrostatic force, and depending on the initial conditions traces a unique chaotic trajectory. Different initial conditions result different behavior; this is a signature of chaotic behavior. To quantify the issues of interest conducive to a better understanding of this nonlinear, chaotic system, we craft this paper as follows. In the analysis section we develop the analytic expressions describing the fundamentals of the coupled two-particle nonlinear system. In numeric section, we deploy Mathematica and for a host of characteristic parameters and initial conditions we analyze the problem numerically; we showcase the results. To get a feel for the chaotic motion utilizing Mathematica animation we bring the chaotic motion of the system alive. We also display a few traditional phase diagrams. Moreover, we introduce a set of fresh, useful phase-type plots as well. We conclude the paper with a few closing remarks.
2. Analysis
Figure 1 shows the system of interest. It is composed of two asymmetric pendulums. Geometrical, mechanical, and electrical properties of each pendulum is given by the respective set of parameters, namely,  , with i = 1,2. The i is the angular position of ith pendulum from the common vertical reference. The pendulums have a common pivot and are allowed to swing in the vertical plane under the influence of the gravity and their mutual repulsive electrostatic force. The weight, tension and the electrostatic forces are designated by {wi,Ti,Fij}, for i,j = 1,2, respectively.
, with i = 1,2. The i is the angular position of ith pendulum from the common vertical reference. The pendulums have a common pivot and are allowed to swing in the vertical plane under the influence of the gravity and their mutual repulsive electrostatic force. The weight, tension and the electrostatic forces are designated by {wi,Ti,Fij}, for i,j = 1,2, respectively.
We consider a case where the movement of the pendulums is confined to a 2-dimansional space. Figure 1 displays a snapshot scenario where each pendulum has assumed an angular position i with respect the vertical reference. The relevant mechanical forces, namely weight and tension are depicted. We also assume the point-like particles are positively (negatively) charged, so that the mutual electrostatic force as shown is repulsive. We swing the pendulums to arbitrary initial positions to within the lower half plane and release them freely. It is the goal of our study to investigate the consequent motion of each bob.
We begin with Newton’s law of motion, namely, . Applying this equation to the 2nd particle along the x and y axis yields,
. Applying this equation to the 2nd particle along the x and y axis yields,  and
and

Figure 1. Display of a coupled two-particle system and their relevant mechanical and electrostatic forces.
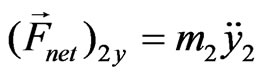 . Here over-dots indicate the second order derivative with respect to time. The x-axis equation yields,
. Here over-dots indicate the second order derivative with respect to time. The x-axis equation yields,
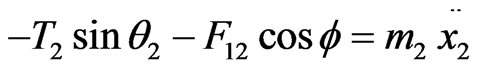 (1)
(1)
Here the mutual electrostatic Coulomb force that particle 1 exerts on 2 is , where = k q1 q2 with k1/(4 p
, where = k q1 q2 with k1/(4 p ) = 8.85 10-12 in MKS units; noting the dimension of is [l] = M L3 T-2. The auxiliary angle shown in Figure 1 is subject to cosf = (x1-x2)/r12. The abscissa of the Cartesian coordinate of the second mass can be substituted in terms of the respective angular positions; utilizing Figure 1,
) = 8.85 10-12 in MKS units; noting the dimension of is [l] = M L3 T-2. The auxiliary angle shown in Figure 1 is subject to cosf = (x1-x2)/r12. The abscissa of the Cartesian coordinate of the second mass can be substituted in terms of the respective angular positions; utilizing Figure 1, . Therefore, in terms of the polar coordinates, cos and x-component acceleration of the second particle reads,
. Therefore, in terms of the polar coordinates, cos and x-component acceleration of the second particle reads, 
 and
and . Substituting these quantities in Equation (1) and rearranging the terms yields,
. Substituting these quantities in Equation (1) and rearranging the terms yields,
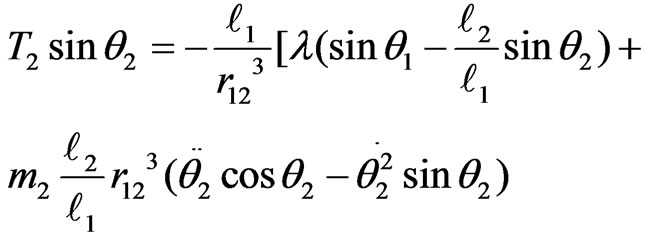 (2)
(2)
Similarly we utilize , this gives,
, this gives,
 (3)
(3)
Following the steps similar the ones outlined in the previous paragraph, utilizing Figure 1, we write, . These yields,
. These yields,
 and
and .Substituting these in Equation (3) and rearranging the terms gives,
.Substituting these in Equation (3) and rearranging the terms gives,
 (4)
(4)
and because and
and
 the distance between the particles i.e. r12 conveniently can be written in terms of the relevant angular position angles,
the distance between the particles i.e. r12 conveniently can be written in terms of the relevant angular position angles,
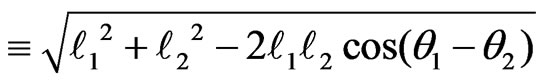 Now we divide Equation (2) by Equation (4). After some tedious, laborious algebraic manipulations we arrive at,
Now we divide Equation (2) by Equation (4). After some tedious, laborious algebraic manipulations we arrive at,
 (5)
(5)
The author based on his own experience is convinced manipulating the ration Equation (2)/Equation(4) yielding Equation (5) is more efficient manually, rather than deploying Mathematica symbolic manipulating utilities!
Now we apply 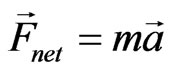 for particle 1. Following the steps similar to what we have already exercised for particle 2 we derive the equation describing the motion of particle 1,
for particle 1. Following the steps similar to what we have already exercised for particle 2 we derive the equation describing the motion of particle 1,
 (6)
(6)
The set of Equations (5) and (6) are to describe the motion of the coupled two-particle system. Each equation of the set is a second order, homogeneous and highly, super nonlinear ODEs. More over, these equations are coupled via a nonlinear, uneven trigonometry function, f[sin(q1-q2), {1,{2,cos(q1-q2)]. Before we attempt solving these equations, we make a few observations. First, it is assuring to realize the lengthy algebraic manipulations of the equations yielding Equations (5,6) have the correct features. Meaning, Equation (5) yields Equation (6) for identical pendulums; i.e. for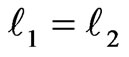 , m1 = m2 and
, m1 = m2 and . This means under these assumptions, the description of the motion of the system is given by only one equation instead of two. Moreover, this one equation is the equation we derived to describing the motion of the symmetrical pendulums in our previous work [1,2]. Second, as we discussed, the non-linearity of the motion has mechanical and electrical origins; these nonlinearities are distinctively separated in Equations (5,6). More specifically, the second and the third coefficients of Equations (5,6) are the strengths of the mechanical and electrical nonlinear terms, respectively. The coefficient of the electric nonlinear term is composed of two distinct elements; l and the rest of the parameters. The value of l as we defined previously is l = k q1 q2. Its value depends on the product of the charges. Assigning different charges to individual particle changes the overall value of the l, however, l contributes evenly to both equations. This is not true for the rest of the charge independent parameters. Meaning, different values of lengths and masses do contribute unevenly. Therefore, the overall value of the coefficient of the electric nonlinear term is different in Equations (5,6). Third, since the electrostatic interaction is the cause of the coupling one expects by stripping the charge(s) the equations describing the motion should reduce the one describing the oscillations of a mechanical nonlinear pendulum. For this scenario we set l = 0; Equations (5,6) yield
. This means under these assumptions, the description of the motion of the system is given by only one equation instead of two. Moreover, this one equation is the equation we derived to describing the motion of the symmetrical pendulums in our previous work [1,2]. Second, as we discussed, the non-linearity of the motion has mechanical and electrical origins; these nonlinearities are distinctively separated in Equations (5,6). More specifically, the second and the third coefficients of Equations (5,6) are the strengths of the mechanical and electrical nonlinear terms, respectively. The coefficient of the electric nonlinear term is composed of two distinct elements; l and the rest of the parameters. The value of l as we defined previously is l = k q1 q2. Its value depends on the product of the charges. Assigning different charges to individual particle changes the overall value of the l, however, l contributes evenly to both equations. This is not true for the rest of the charge independent parameters. Meaning, different values of lengths and masses do contribute unevenly. Therefore, the overall value of the coefficient of the electric nonlinear term is different in Equations (5,6). Third, since the electrostatic interaction is the cause of the coupling one expects by stripping the charge(s) the equations describing the motion should reduce the one describing the oscillations of a mechanical nonlinear pendulum. For this scenario we set l = 0; Equations (5,6) yield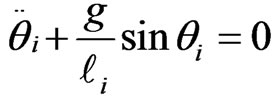 , for i = 1,2. The latter for small angle approximation i.e. for a linear oscillator yields the classic linearized equation of motion of a simple pendulum,
, for i = 1,2. The latter for small angle approximation i.e. for a linear oscillator yields the classic linearized equation of motion of a simple pendulum,  , for i = 1,2.
, for i = 1,2.
Now that we have confidence in the correctness of the format of the derived equations, we step forward attempting solving them. Because the equations include generic parameters describing the individual pendulum, we have the option of assigning a wide range of parameters to characterize each pendulum. For instance, one may consider two pendulums with two different lengths but the same parameters otherwise. Since the third coefficient of Equations (5,6) depends on the ratio of the lengths of the pendulums, then for instance in one scenario one may study the subsequent impact of assigning rational or irrational and real values to the ratio. Practicing one such option would open the “Pandora box”. Analyzing the impact of one such scenario maybe addressed in another research project. For time being in the following section we study a subset of such options showcasing our findings.
3. Numerical Analysis
In the previous section we applied fundamentals of physics principles and developed a set of equations describing the motion of the system. These equations of motion are given with a set of coupled homogeneous highly, super nonlinear ODEs, namely Equations (5,6). To pin point the angular position of each bob at a given time t, one needs to solve these equations expressing angular positions as explicit functions of time, namely {q1(t), q2(t)}. In our first attempt to solving these equations we apply various standard symbolic methods. The super non-linearity of the equations come about from the electrostatic coupling term, the third terms of Equations (5,6). These are complicated trigonometric two variable functions. No wonder we fail solving these equations symbolically. We then apply Mathematica DSolve command; it is also unable producing any output. As a last resource we pursue solving these equations numerically. We begin with selecting a set of physically reasonable parameters describing the pendulums, such as {l,m,q}. Then we set the initial conditions, i.e. the initial swing angles of the pendulums. With these parameters on hand, we apply Mathematica NDSolve; it solves the equations. According to the aforementioned description the code reads:
In MKS units the pendulums are characterized by, values = {{1®1.0, m1®8.*10-3,m2®8.*10-3,q1® 1.* 1.*10-6,q2®1.* 10-6,k®9 *109,g®9.8};
In this example the pendulums are nonidentical; their initial swing angles are different. One is set at p/4and the other one is at 1.2 p/4.
{{2,q1init,q2init,tmax} = {1.0,1.2 p/4,p/4,100.};
The coefficients of the second and the third terms of Equations (5,6) contain the mechanical and the electrostatic coupling parameters and are defined by {a’s,b’s}; {a1,b1} for the first and {a2,b2} for the second pendulum.
{{a1,b1},{a2,b2}}={{g/{1,(k q1 q2)/(m1 {13)}{g/{2,(k q1 q2)/(m2 {23)}}/.values;
The denominators of the third terms in Equations (5) and (6) are noted by r21 and r12, respectively. Noting, r21=r12/.{{1®{2,{2®{1}
r21=(1+({2/{1)2-2 {2/{1Cos[q1[t]-q2[t]])/.values;
r12=(1+({1/{2)2-2 {1/{2Cos[q1[t]-q2[t]])/.values;
We form the ODE’s given by Equations (5,6), these areeqnq1=q1''[t]+a1Sin[q1[t]]-b1{2/{1Sin[q1[t]-q2[t]]/ .values;
.values;
eqnq2=q2''[t]+a2Sin[q2[t]]+b2{1/{2Sin[q1[t]-q2[t]]/  /.values;
/.values;
Utilizing NDSolve we assume symmetrical initial conditions and drop the pendulums freely, evenly about the vertical reference through the common pivot. When invoking NDSolve, we imply the option MaxSteps ®¥ otherwise for most of the cases of interest the default numeric solution routine search stops after 1000 iterations without searching the desired time span.
soleqns=NDSolve[{eqnq10,eqnq20,q1[1x 10-8]q1init,q1'[1*10-8]0,q2[1*10-8]q2init,q2'[1* 10-8]0},{q1[t],q2[t]},{t,1*10-8,tmax},MaxSteps®¥];
Utilizing the suppressed output of the numeric solutions we evaluate the kinematic quantities of interest such as, position, speed and acceleration of the individual pendulum. These set are characterized by Kinq1 and kinq2.
kinq1={positionq1,speedq1,accq1}=Table[D[q1[t]/.soleqnsP1]],{t,n}],{n,0,2}];
kinq2={positionq2,speedq2,accq2}=Table[D[q2[t]/.soleqnsP1]],{t,n}],{n,0,2}];
The next couple of lines are used to animate the motion of the swinging pendulums.
x1y1:={{1Sin[q1[t]/.soleqnsP1]]/.values,-{1 os[q1[t]/.soleqnsP1]]/.values}
x2y2:={{2Sin[q2[t]/.soleqnsP1]]/.values,-{2 Cos[q2[t]/.soleqnsP1]]/.values}
tabx1y1=Table[x1y1,{t,0,tmax,0.05}];
tabx2y2=Table[x2y2,{t,0,tmax,0.05}];
Applying Manipulate we display an alive movement of the pendulums. This helps to gain a visual understanding about how the proposed system behaves for the chosen set of parameters. The display panel includes also additional helpful diagrams such as the time series of the angular positions of the pendulums, phase profile of the pendulums, and the parametric plot of the angular position of one of the pendulums vs. the other.
Manipulate[{{Show[Graphics[{Line[{{-2,0},{2.0,0}}],Line[{{0,-2},{0,2.5}}],{Hue[0.7],Line[{{0,0},tabx1y1Pn]}]},{PointSize[0.025],Hue[0.0],Point[tabx1y1Pn]]}, {Hue[0.],Line[{{0,0},tabx2y2Pn]}]},{PointSize[0.025],Hue[0.],Point[tabx2y2Pn]]}}],ImageSize®250,PlotRange®{{-2,2},{-2,1}}],Plot[{180/pEvalate[q1[t]/.soleqnsP1]],180/pEvaluate[q2[t]/.soleqnsP1]]},{t,1 10-8,tmax-10.},AxesLabel®{"t,s","q1,q2"},PlotStyle®{Blue,Red}]},{ParametricPlot[Flaten[{kinq2P1]],kinq2P2]]}],{t,1*10-8,tmax-50},AxesLabel®{" ","
"," "},AspectRatio®1,PlotRange®All,PlotStyle®Red]ParametricPlot[Flatten[{kinq1P1]],kinq1P2]]}],{t,1* 10-8,tmax-50.},AxesLabel®{"
"},AspectRatio®1,PlotRange®All,PlotStyle®Red]ParametricPlot[Flatten[{kinq1P1]],kinq1P2]]}],{t,1* 10-8,tmax-50.},AxesLabel®{" ","
"," "},AspectRatio®1,PlotRange®All,PlotStyle®Blue]ParametricPlot[Flatten[{kinq1P1]],kinq2P1]]}],{t,1* 10-8,tmax-50},AxesLabel®{"q1","q2"},AspectRatio®1,PlotRange®All,PlotStyle®Black]
"},AspectRatio®1,PlotRange®All,PlotStyle®Blue]ParametricPlot[Flatten[{kinq1P1]],kinq2P1]]}],{t,1* 10-8,tmax-50},AxesLabel®{"q1","q2"},AspectRatio®1,PlotRange®All,PlotStyle®Black]
}
},{{n,1,"frame"}, 1,Length[tabx1y1],1}]
To show the impact of the initial conditions on the behavior of the system, in Figure 4 we display plots similar the one shown in Figure 3. The only difference parameterizing the system is the initial swing angle of the left side pendulum; it is set at . For instance the phase profile of the first pendulum displaced by the first graphs of the Figures 3,4 are quite distinguishable. Also the difference between the left lower graphs, the parametric plots of the angular position of the second pendulum vs. the first one is drastic. These very much resemble the Lissajous curves.
. For instance the phase profile of the first pendulum displaced by the first graphs of the Figures 3,4 are quite distinguishable. Also the difference between the left lower graphs, the parametric plots of the angular position of the second pendulum vs. the first one is drastic. These very much resemble the Lissajous curves.
Note, a classic Lissajous curve is referred to a closed curve that is being traced by one particle subject to simultaneous harmonic motions in two perpendicular directions. In our study the Lissajous curves are traced by combining the oscillations of two particles subject to oscillations of with a relative arbitrary phase difference.
Reviewing Figures 2-7 reveals for the chosen set of initial conditions the motion of the each pendulum is chaotically deterministic. That is to say there should be a relation such as  for i = 1,2. Where qi,n is the angular position of one of the pendulums at a sampled time and f is the mapping procedure. In its simplest form we explore the existence of one such possibility following procedure outlined in [3] i.e. we plot qi,n+1 vs. qi,n, these are shown in Figure 9. According to these plots and according to our speculations, indeed the time series depicted in Figure 2, are not noise, rather underline a deterministic chaotic behavior. Interested reader utilizing the embedded code may explore similar plots for various possible characteristic parameters some have
for i = 1,2. Where qi,n is the angular position of one of the pendulums at a sampled time and f is the mapping procedure. In its simplest form we explore the existence of one such possibility following procedure outlined in [3] i.e. we plot qi,n+1 vs. qi,n, these are shown in Figure 9. According to these plots and according to our speculations, indeed the time series depicted in Figure 2, are not noise, rather underline a deterministic chaotic behavior. Interested reader utilizing the embedded code may explore similar plots for various possible characteristic parameters some have

Figure 2. Top row from left to right: a snapshot of the animation, the time series of the pendulums. Second row: the phase profile of the left (Red) and the right (Blue) pendulums, the parametric plot of the angular positions of the second pendulum vs. the first.


Figure 3. An extended graphic version of the plots of Figure 2. The second and third plots of the first and the second row are fresh additions to our classic/traditional plots.


Figure 4. The impact of the initial angle on the characteristic behavior of the system. The initial angle for the left particle is set at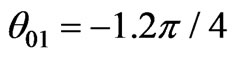 .
.


Figure 5. Same as Figure 4, with the exception of instead of identical masses we assumed m1 = 12/8 m2.


Figure 6. Same as Figure 4, with the exception of the length of the left side pendulum is .
.
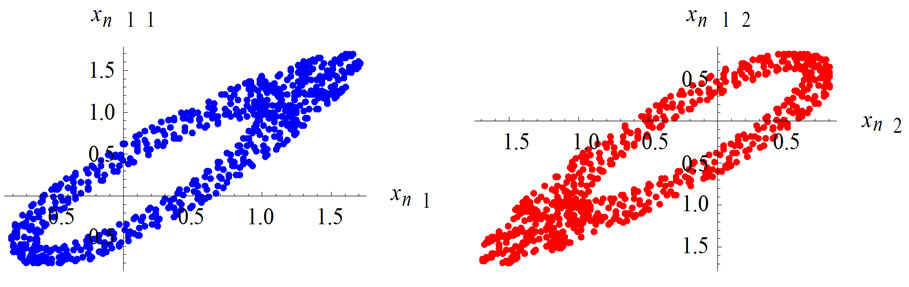
Figure 8. Plots of  vs.
vs.  for i = 1,2. The left graph depicts the first pendulum and the right graph shows the second pendulum. Parameters are as the same used in Figure 2.
for i = 1,2. The left graph depicts the first pendulum and the right graph shows the second pendulum. Parameters are as the same used in Figure 2.
been discussed in the text.
tabq1=Table[{N[t],q1[t]/.soleqnsP1]]},{t,1*10-8,tmax,0.15}];
tabq2=Table[{N[t],q2[t]/.soleqnsP1]]},{t,1* 10-8,tmax,0.15}];
tabq1n=Table[tabq1Pn,2]],{n,Length[tabq1]-1}];
tabq2n=Table[tabq2Pn,2]],{n,Length[tabq2]-1}];
tabq1nplus1=Table[tabq1Pn+1,2]],{n,Length[tabq1]-1}];
tabq2nplus1=Table[tabq2Pn+1,2]],{n,Length[tabq2]-1}];
transposeNNplus1=Transpose[{tabq1n,tabq1nplus1}];
transposeNNplus2=Transpose[{tabq2n,tabq2nplus1}];
s1=ListPlot[transposeNNplus1,PlotStyle®{Blue},PlotRange®All,AxesLabel®{"(xn)1","(xn+1)1"}];
s2=ListPlot[transposeNNplus2,PlotStyle®{Red},PlotRange®All,AxesLabel®{"(xn)2","(xn+1)2"}];
GraphicsArray[{s1,s2},ImageSize®400]
4. Conclusions
It is the objective of our analysis to explore real-life cases conducive to nonlinear physical phenomena. We suggest a system composed of a pair of charged pendulums that are free to oscillate in a vertical plane under the gravity pull and mutual electrostatic interaction. In addition to the large angle oscillations which by itself is a source of nonlinear oscillations we include the electrostatic interaction. As we show, the latter contributes strongly to the non-linearity of the oscillations. We formulate the problem at hand symbolically for a general case. The system under the consideration describes a general setting of its kind. This is a major modification vs. of our previous work where only symmetrical, identical pendulums were considered. Applying Mathematica we analyze the problem numerically. From this analysis we gain a valuable insight about the chaotic motion. For a comprehensive understanding we showcase our findings. We conclude the paper pointing to the deterministic chaotic behaviors of the system. The plot of angular position of one of the pendulums vs. the other traces a Lissajous type curve. We show the chaotic behavior of the system underlines an attractor. The paper includes a series of Mathematica codes assisting the interested reader to investigate the problem further.