1. Introduction
Prime numbers are numbers that can be divided only by one or by themselves in order to get integer number. They are probably the most famous number’s series. For finding the primes up to N, 2 main Sieves have been developed. One is the Eratosthenes Sieve [1] that is based on eliminating the not prime that is generated by multiplies of numbers over a list. For this Sieve the complexity is . Another Sieve is the Atkins and Bernstein Sieve [2,3], which is based on the remainder of modulo sixty.
. Another Sieve is the Atkins and Bernstein Sieve [2,3], which is based on the remainder of modulo sixty.
In this case the complexity is . This paper aims to continue on this work improving the sieving. Observe that all the odd numbers are not prime if they are of the form
. This paper aims to continue on this work improving the sieving. Observe that all the odd numbers are not prime if they are of the form
 (2)
(2)
where p is a prime number > 1 and  and np is for not prime.Taking all the numbers for x odd where the set of the odds is bigger than the set of prime, and k integer is possible to cover all the Not Prime set. There are some repetition in particular those that have remainder 0 divided by 3 (Of course the x = 3 series must be generated first and after a number np can be considered not prime already counted if divided by 3 gives remainder 0). In the first algorithm we give a solution with repetition in building the set of not prime. In the second we avoid the repetition considering that a square number generated from an odd, generate vary k, two possible kind of repetition: in the first is repeated for each k (mod 3) = 2, and in the second for each k (mod 3) = 3.
and np is for not prime.Taking all the numbers for x odd where the set of the odds is bigger than the set of prime, and k integer is possible to cover all the Not Prime set. There are some repetition in particular those that have remainder 0 divided by 3 (Of course the x = 3 series must be generated first and after a number np can be considered not prime already counted if divided by 3 gives remainder 0). In the first algorithm we give a solution with repetition in building the set of not prime. In the second we avoid the repetition considering that a square number generated from an odd, generate vary k, two possible kind of repetition: in the first is repeated for each k (mod 3) = 2, and in the second for each k (mod 3) = 3.
2. Methods
2.1. Method I
The follow is a explanation of the method for the search of prime. We want to count the prime up to N. We extend our iteration variable in the interval . The numbers (mod 2) = 0 are not primes. For the prime number we generate first
. The numbers (mod 2) = 0 are not primes. For the prime number we generate first  as not prime and after generate
as not prime and after generate . With p that can be an also an odd number because the set of primes is in the set of odds except that number 2 and
. With p that can be an also an odd number because the set of primes is in the set of odds except that number 2 and . The algorithm is presented in the appendix.
. The algorithm is presented in the appendix.
2.2. Method II
Another better result can achieved thinking that the numbers (mod 3) = 0, repeat in the count. I observed that there are 3 kind of repetition.  for every k like
for every k like .
.  for every k counted 1 (not counted 0) in the sequence 101-101-101 like 5. And for every k in the sequence 110-110-110 like 7.
for every k counted 1 (not counted 0) in the sequence 101-101-101 like 5. And for every k in the sequence 110-110-110 like 7.
We should make it in a way that affords us to go over a case of 0 and go to next k = k + 1, avoiding count repetition.
Example 7 × 7 = 49 (mod 3 different from 0) not counted; 7 × 7 + 2 × 7 = 63 (mod 3 = 1) already counted in the 3 sequence; 7 × 7 + 4 × 7 = 77 not counted. They gives the sequence 101.
3. Results
To count the primes up to 1,000,000 both methods take 3 seconds. This means that only for bigger N a comparison of methods is possible. The second should anyway take less time than the first. The test has been done with an machine Asus Intel i7 with 4 GB Ram, with an Operative System Windows 7 and the platform Java.
Appendix
Algorithm I
N we count the prime up to N primes [N] = true for each element

for 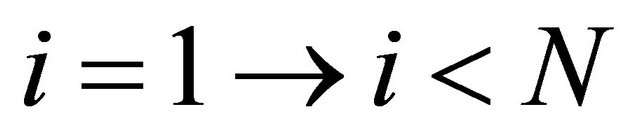 do primes [i] = false
do primes [i] = false

wang#title3_4:spend for
for  do
do

while  do if
do if  ||
||  then
then

end if

end while

wang#title3_4:spend for
return primes
Computational Complexity of Algorithm I
We call C(A) the complexity of the second loop, whereas, T(A) is the complexity of all the code.

We use the approximation
 (3)
(3)
as stated in [4]
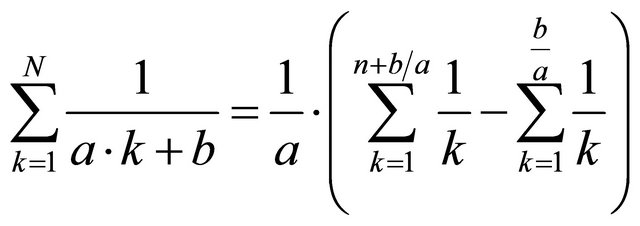 (4)
(4)
and
 (5)
(5)
as stated in [5,6]
The complexity of the first method is given by the 2 nested loop in the algorithm.

Separating the members of addition

Evaluating the second member with (3)

Taking out of the first member the constant operation

Changing the form for odd number at first member

Extending the sum adding and subtracting the same element

Using the (4)
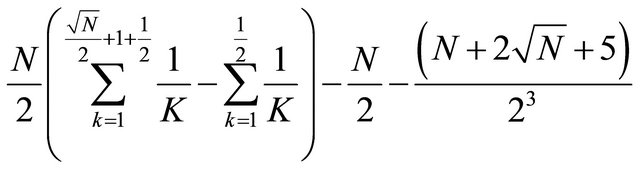
Using the (5)

That asymptotically goes like

Algorithm II
N we want to count the primes until N primes [N] = true

for  do primes [i] = false
do primes [i] = false
end if
for 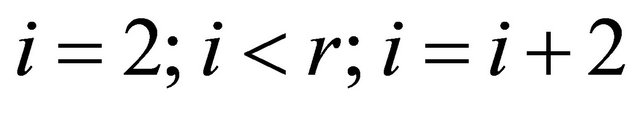 do
do

j = square k = 0 condition = "";
if  mod 3 == 0 And
mod 3 == 0 And  then condition = "101";
then condition = "101";
else if  mod 3 == 0 And
mod 3 == 0 And  then condition = "110"
then condition = "110"
else if  then condition = "111"
then condition = "111"

end if
while  And! ("111") do if j mod 3! = 0 or i == 2 then
And! ("111") do if j mod 3! = 0 or i == 2 then

wang#title3_4:spwang#title3_4:spend if

if condition = ("101") And  then
then

wang#title3_4:spwang#title3_4:spend if
if condition = ("110") And  then
then

wang#title3_4:spwang#title3_4:spend if

end while
end for
returns primes