1. Introduction and Definitions
In vector spaces and linear maps; topological spaces and continuous maps; groups and homomorphisms together with the distinguished family of maps is referred to as a category. An operator which assigns to every object in one category a corresponding object in another category and to every map in the first a map in the second in such a way that compositions are preserved and the identity map is taken to the identity map is called a functor. Thus, we may summarize our activities thus far by saying that we have constructed a functor (the fundamental group functor) from the category of pointed spaces and maps to the category of groups and homomorphisms. Such functors are the vehicles by which one translates topological problems into algebraic problem El-Ahmady [1-3].
Most folding problems are attractive from a pure mathematical standpoint, for the beauty of the problems themselves. The folding problems have close connections to important industrial applications Linkage folding has applications in robotics and hydraulic tube bending. Paper folding has application in sheet-metal bending, packaging, and air-bag folding. Following the great Soviet geometer, also, used folding to solve difficult problems related to shell structures in civil engineering and aero space design, namely buckling instability El-Ahmady [4]. Isometric folding between two Riemannian manifold may be characterized as maps that send piecewise geodesic segments to a piecewise geodesic segments of the same length El-Ahmady [5]. For a topological folding the maps do not preserves lengths ElAhmady [6] and [7]. i.e. A map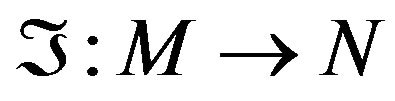 , where
, where  and N are
and N are  -Riemannian manifolds of dimension m and n respectively is said to be an isometric folding of M into N, iff for any piecewise geodesic path
-Riemannian manifolds of dimension m and n respectively is said to be an isometric folding of M into N, iff for any piecewise geodesic path , the induced path
, the induced path  is a piecewise geodesic and of the same length as
is a piecewise geodesic and of the same length as . If
. If  does not preserve length, then
does not preserve length, then  is a topological folding El-Ahmady [8, 9].
is a topological folding El-Ahmady [8, 9].
A subset A of a topological space X is called a retract of X if there exists a continuous map  such that
such that  where A is closed and X is open El-Ahmady [10] and [11]. Also, let X be a space and A a subspace. A map
where A is closed and X is open El-Ahmady [10] and [11]. Also, let X be a space and A a subspace. A map  such that
such that  is called a retraction of X onto A and A is the called a retract of X El-Ahmady [12-19] Reid [20]. This can be re stated as follows. If
is called a retraction of X onto A and A is the called a retract of X El-Ahmady [12-19] Reid [20]. This can be re stated as follows. If  is the inclusion map, then
is the inclusion map, then  is a map such that
is a map such that . If, in addition,
. If, in addition,  , we call
, we call  a deformation retract and A a deformation retract of X Arkowitz [21]. Another simple but extremely useful idea is that of a retract. If
a deformation retract and A a deformation retract of X Arkowitz [21]. Another simple but extremely useful idea is that of a retract. If  then
then is a retract of
is a retract of  if
if  . If
. If  and
and , then f is a retract of
, then f is a retract of  if
if  and
and  [13,14].
[13,14].
i.e. If  and
and  then f is a retract of
then f is a retract of  if there is a commutative diagram.
if there is a commutative diagram.

that is,  ,
, ,
,  ,
,  , and fr = sg Shick [22] and Storn [23]. The elastic manifold
, and fr = sg Shick [22] and Storn [23]. The elastic manifold  is a manifold
is a manifold  attached with
attached with ,
,  is the coefficient of elasticity, i.e.
is the coefficient of elasticity, i.e. . If
. If , then
, then , the usual manifold, and
, the usual manifold, and  is the complete manifold also for an elastic manifold
is the complete manifold also for an elastic manifold , the distance
, the distance  between any two points
between any two points  is not constant. The aim of this paper is to describe the connection between the fundamental group and the homotopy group geometrically, specifically concerned with the study of the new type of retraction, deformation retract, folding and the fundamental group of elastic Klein bottle as presented by El-Ahmady [1,2].
is not constant. The aim of this paper is to describe the connection between the fundamental group and the homotopy group geometrically, specifically concerned with the study of the new type of retraction, deformation retract, folding and the fundamental group of elastic Klein bottle as presented by El-Ahmady [1,2].
2. Main Results
To obtain the main results, we will introduce the following definition.
The Klein bottle  can be realized as a parametric surface in
can be realized as a parametric surface in . At each point of the circle of radius a in the
. At each point of the circle of radius a in the  plane there is now available a three-dimensional hyperplane in
plane there is now available a three-dimensional hyperplane in  perpendicular to the circle. A smaller circle of radius
perpendicular to the circle. A smaller circle of radius  can be rotated about a diameter at half the rate of revolution about the circle of radius
can be rotated about a diameter at half the rate of revolution about the circle of radius , giving a Klein bottle Shick [2,3]. The parameterization is given analytically as follows
, giving a Klein bottle Shick [2,3]. The parameterization is given analytically as follows
 (1)
(1)
Points in Points in the  plane which are identified as indicated in Figure 1 are mapped into the same points in
plane which are identified as indicated in Figure 1 are mapped into the same points in  by these equations.
by these equations.
From view point of elastic manifold if  are variables and instance
are variables and instance . Hence the parameterization of elastic Klein bottle is given analytically and (1) becomes
. Hence the parameterization of elastic Klein bottle is given analytically and (1) becomes
 (2)
(2)
The metric of elastic Klein bottle is given by
 . (3)
. (3)
Theorem 1. The fundamental group of types of the deformation retracts of open elastic Klein bottle  is isomorphic to Z.
is isomorphic to Z.
Proof. Now we will prove that  and
and  are the deformation retract of open elastic Klein bottle
are the deformation retract of open elastic Klein bottle . Using Lagrangian equations to obtain a geodesics and retractions of elastic Klein bottle
. Using Lagrangian equations to obtain a geodesics and retractions of elastic Klein bottle . From Equation
. From Equation
(3) we get

Then, the Lagrangian equations for elastic Klein bottle  are
are
 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
solving Equation (4) implies
 consider the case
consider the case , and and
, and and . Then we are going to discuss the following cases
. Then we are going to discuss the following cases
(i) If , then
, then , where c and a are constant. If
, where c and a are constant. If , then
, then , which means that the deformation of the manifold is regular (the piecewise geodesic deformed into piecewise geodesic). Now, if
, which means that the deformation of the manifold is regular (the piecewise geodesic deformed into piecewise geodesic). Now, if , then
, then , and the piecewise geodesic deformed into non-piecewise geodesic and the deformation of the elastic manifold is not regular and (5) becomes
, and the piecewise geodesic deformed into non-piecewise geodesic and the deformation of the elastic manifold is not regular and (5) becomes
 ,
,
 ,
,
 ,
,
 .
.
which is the elastic hyper Klein bottle . It is not a geodesic.
. It is not a geodesic.
(ii) If , then
, then , also from Equation (5) we have
, also from Equation (5) we have
 ,
,
 ,
,
 ,
,
 .
.
which is the elastic hyper Klein bottle  which is not a geodesic.
which is not a geodesic.
Now,  can be true only for
can be true only for  and (5) becomes
and (5) becomes
 ,
,  ,
, 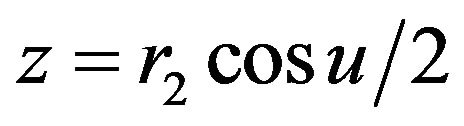 ,
, .
.
Which is the elastic hyper sphere  which is a geodesic.
which is a geodesic.
(iii) If , then
, then  constant
constant
 , if
, if , there are two geodesics in elastic Klein bottle
, there are two geodesics in elastic Klein bottle  given by
given by ,
,  ,
,  .
.
Which is the elastic great circle. . Also,
. Also,
 ,
,  ,
, .
.
Which is the elastic great circle 
(iv) If , then
, then  constant
constant , if
, if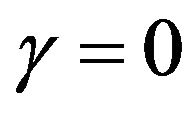 . Hence the coordinate of elastic Klein bottle are
. Hence the coordinate of elastic Klein bottle are

which is the elastic hyper Klein bottle , it is a geodesic. Also, if
, it is a geodesic. Also, if , then we obtain the following geodesic
, then we obtain the following geodesic  given by
given by

It follows immediately that. 
 is a geodesic. The deformation retract of the elastic Klein bottle
is a geodesic. The deformation retract of the elastic Klein bottle  may be defined as follows
may be defined as follows
 .
.
Also, the retraction of the elastic Klein bottle is defined as follows:  or
or  or
or  or
or  or
or  or
or  or
or .
.
The deformation retract of (2) into a retraction  is given by
is given by

where

and .
.
Thus, . Therefore
. Therefore
 .
.
Also, the deformation retract of (2) into a retraction  is defined as
is defined as

where
 and
and .
.
Thus, .
.
Therefore .
.
Corollary 1. The fundamental group of types of the deformation retracts of open elastic Klein bottle  and any manifold homeomorphic to elastic Klein bottle
and any manifold homeomorphic to elastic Klein bottle  is isomorphic to Z.
is isomorphic to Z.
Theorem 2. The fundamental group of any folding of elastic great circle  and elastic great circle
and elastic great circle  is either isomorphic to Z or identity group.
is either isomorphic to Z or identity group.
Proof. Now, we are going to discuss the folding  of
of  and
and .
.
Let  where
where

also let  where
where

An isometric folding of
of  into itself may be defined by
into itself may be defined by
 .
.
Also, an isometric folding of
of  into itself may be defined by
into itself may be defined by

This type of folding and any folding homeomorphic to this folding induce singularity of , and
, and 
thus  also
also . Now, if the folding is defined as
. Now, if the folding is defined as
 , and
, and
 this type of folding and also any folding homeomorphic to this folding not induce singularity of
this type of folding and also any folding homeomorphic to this folding not induce singularity of ,
,  and any manifold homeomorphic to
and any manifold homeomorphic to ,
,
 . Then
. Then  and
and .
.
Corollary 2. The fundamental group of types of geodesic in elastic Klein bottle can be considered as the fundamental group of types of a deformation retract in elastic Klein bottle.
Theorem 3. The fundamental group of types of the deformation retracts of the elastic Klein bottle is either a fundamental group of types of the geodesics or not and its folding may be the fundamental group of types of the deformation retracts or not.
Theorem 4. The fundamental group of the limit of foldings of the elastic hyper sphere  is the identity group.
is the identity group.
Proof. Now consider the elastic hyper sphere of dimension three  which is a geodesic in elastic Klein bottle and let
which is a geodesic in elastic Klein bottle and let  is a folding map ,now we can define a series of folding maps by
is a folding map ,now we can define a series of folding maps by
 ,
,
 ,
,
 ,
,



is a sphere  of dimension two. Therefore
of dimension two. Therefore
 is the identity group.
is the identity group.
Theorem 5. Under the folding
 , the fundamental group of the limit of foldings of the elastic hyper sphere
, the fundamental group of the limit of foldings of the elastic hyper sphere 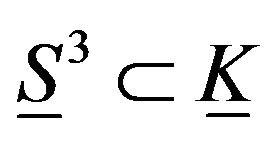 in elastic Klein bottle is isomorphic to Z.
in elastic Klein bottle is isomorphic to Z.
Proof. Now consider the elastic hyper sphere of dimension three  which is a geodesic in elastic Klein bottle and if we let
which is a geodesic in elastic Klein bottle and if we let

 be given by
be given by

Then, the isometric chain folding of the elastic hypersphere  into itself may be defined by
into itself may be defined by
 ,
,
 ,
,
 ,
,
 .
.
Then we get
 which is the elastic great circle
which is the elastic great circle 
Therefore 
Theorem 6. Under the folding
 , the fundamental group of the limit of foldings of the elastic hyper sphere
, the fundamental group of the limit of foldings of the elastic hyper sphere  in elastic Klein bottle is the identity group.
in elastic Klein bottle is the identity group.
Proof. Consider the elastic hyper sphere of dimension three  which is a geodesic in elastic Klein bottle and if we let
which is a geodesic in elastic Klein bottle and if we let  be given by
be given by

Then, the isometric chain folding of the elastic hyper sphere into itself may be defined by
 ,
,



Then we get  , which a zerodimensional hypersphere
, which a zerodimensional hypersphere  in elastic Klein bottle. Thus, it is a point and the fundamental group of a point is the identity group.
in elastic Klein bottle. Thus, it is a point and the fundamental group of a point is the identity group.
Corollary 3. The fundamental group of the end limits of foldings of the n-dimensional manifold  homeomorphic n-dimensional elastic Klein bottle
homeomorphic n-dimensional elastic Klein bottle  into itself is the identity group.
into itself is the identity group.
Proof. let  be a type of foldings of ndimensional manifold
be a type of foldings of ndimensional manifold  . Then, we have the following chains
. Then, we have the following chains


 ,
,

Thus from the above chain the end of the limits of folding coincides with the zero-dimensional manifold. Thus, it is a point and the fundamental group of a point is the identity group.
Theorem 7. The fundamental group of the minimal retraction of the n-dimensional manifold  homeomorphic n-dimensional elastic Klein bottle
homeomorphic n-dimensional elastic Klein bottle  is the identity group.
is the identity group.
Proof. let  be the retractions map. Then, we have the following chains
be the retractions map. Then, we have the following chains




Thus from the above chain the minimal retractions of the n-dimensional manifold  coincides with the zerodimensional space which is the limit of retractions. Thus, it is a point and the fundamental group of a point is the identity group.
coincides with the zerodimensional space which is the limit of retractions. Thus, it is a point and the fundamental group of a point is the identity group.
Theorem 8. The fundamental group of the end of the limits of folding of the n-dimensional manifold  homeomorphic n-dimensional elastic Klein bottle
homeomorphic n-dimensional elastic Klein bottle  coincides with the fundamental group of the minimal retractions of the n-dimensional manifold
coincides with the fundamental group of the minimal retractions of the n-dimensional manifold .□
.□
3. Conclusion
In this paper we achieved the approval of the important of the fundamental groups in the submanifolds of elastic Klein bottle by using some geometrical transformations. The relations between foldings, retractions, deformation retracts, limits of foldings and limits of retraction of the fundamental groups in the submanifolds of elastic Klein bottle are discussed. The connection between limits of the folding and the fundamental groups are obtained. New types of minimial retractions on the fundamental groups are deduced.
4. Acknowledgements
The author is deeply indebted to the team work at the deanship of the scientific research, Taibah University for their valuable help and critical guidance and for facilitating many administrative procedures. This research work was financed supported by Grant No. 3066/1434 from the deanship of the scientific research at Taibah University, Al-Madinah Al-Munawwarah, Saudi Arabia.