1. Introduction
Special relativity presupposes a smooth space-time with Lorentzian symmetry group invariance [1]. Quantum space-time on the other hand is modelled via radically different geometrical realization [1-8]. In string theory, M-theory and super gravity one uses various types of Calabi-Yau and complex Kähler manifolds for spacetime extra dimensions [9-17]. Consequently requiring Poincaré invariance in a complex space with extra dimensions will most surely lead to a different energymass relation than the classical equation of special relativity. Should the principle of scale relativity hold, then one would expect to retrieve Einstein’s familiar formula in a scaled form [3-5]. Noting that for a continuous manifold the Betti number  which counts the three dimensional holes in a manifold is given by
which counts the three dimensional holes in a manifold is given by 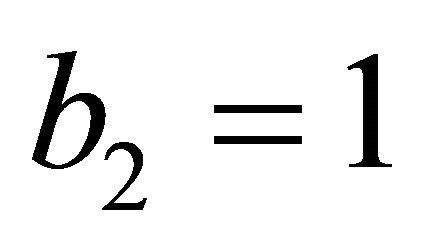 and that the same Betti number for a K3 Kähler is
and that the same Betti number for a K3 Kähler is , it is possible to show that E = m0c2 may be elevated to a quantum relativity, i.e. a quantum gravity equation when scaled by
, it is possible to show that E = m0c2 may be elevated to a quantum relativity, i.e. a quantum gravity equation when scaled by 
This prior intuitive expectation noted first by El Naschie was confirmed later on by him on two counts, namely first experimentally using the cosmic measurement of Ries, Schmidt and Perlmutter [4] and second theoretically using numerous sophisticated established theories, all leading to the same robust result, namely .
.
In this paper we show following El Naschie that for a fuzzy Kähler [10,13], the scaling factor changes from
 to
to . In addition to giving a derivation of
. In addition to giving a derivation of  where m0 is the controversial rest mass and c is the speed of light, we show that this result is in exquisite agreement with the cosmological measurement of COBE and WMAP as well as the analysis of certain supernovas which led to the award of last year’s 2011 Nobel Prize in Physics [4]. Based on K3 fuzzy Kähler, one can predict with very high precision that the percentage of hypothetical dark energy missing in the universe is 95.4915028 percent. This is a potentially unprecedented agreement between theory and measurement in cosmology, if not in all of theoretical physics [1]. We probably will know for sure when the Planck measurement project is completed. However this particular result of El Naschie has in one giant leap unified many theories, old and new, and reconciled theory with measurement [16-19]. In Table 1 we summarize the results of various theories and methods leading to the same energy reduction factor of almost
where m0 is the controversial rest mass and c is the speed of light, we show that this result is in exquisite agreement with the cosmological measurement of COBE and WMAP as well as the analysis of certain supernovas which led to the award of last year’s 2011 Nobel Prize in Physics [4]. Based on K3 fuzzy Kähler, one can predict with very high precision that the percentage of hypothetical dark energy missing in the universe is 95.4915028 percent. This is a potentially unprecedented agreement between theory and measurement in cosmology, if not in all of theoretical physics [1]. We probably will know for sure when the Planck measurement project is completed. However this particular result of El Naschie has in one giant leap unified many theories, old and new, and reconciled theory with measurement [16-19]. In Table 1 we summarize the results of various theories and methods leading to the same energy reduction factor of almost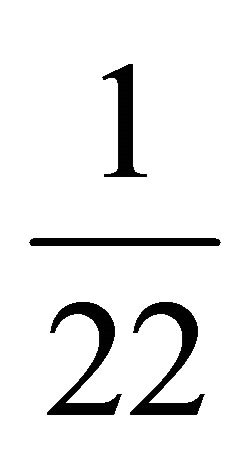 .
.
2. Motives for Revising Einstein’s Energy-Mass Equation
As aptly noted by El Naschie, an equation based entirely on a smooth space with Lorentzian space-time invariance developed years before quantum mechanics was formulated by Heisenberg, Schrödinger and Dirac could not possibly be expected not to break down at some quantum or intergalactic scale [1-3]. In the present short paper we show following El Naschie that the missing dark energy in the cosmos, discovered through various accurate cosmological measurements [4] is due to some basic fundamental inadequacies of applying Einstein’s celebrated equation E = m0c2 where E is the energy, m0 is the rest mass and c is the speed of light outside its range of validity [5,6]. We thought for a long time and understandably so that gravity cannot have that crucial effect on elementary particle physics. Similarly we thought that quantum mechanics also has very little effect on cosmology except maybe when it comes to incredibly shrinking objects such as black holes [1].
However when we started asking very deep questions regarding the unification of all fundamental interactions [7,8] we recognized suddenly that at the extreme small distance such as the Planck length (10−33 cm) the feeble gravity becomes as strong as the other three fundamental forces, i.e. the weak force, the strong force and the electromagnetic force [1,3,7]. On the other hand we now just realize that quantum effect such as quantum entanglement has an impact on physics at extremely large intergalactic distances. It is so profound that the classical equation of Einstein E = m0c2 is off the correct result by almost 95.5% [4]. Seen with the eyes of a particle physicist this should not be that astonishing because the only degree of freedom of special relativity is a single messenger particle, the photon. By contrast the simplest model for high energy quantum physics, the standard model, needs 12 messenger particles equivalent to 12 degrees of freedom. Special relativity is highly confined by the Rayleigh theorem on Eigen value and is bound to overestimate energy levels.
In the present work we trace back the deficiency in E = m0c2 and prove that this is the case because of the real non-classical geometry and topology of the actual fabric of space-time [2,7,8]. This non-classical topology is essentially the cause of amplifying what we perceive as
Table 1. Result of some of the various theories applied to dark energy by El Naschie and E-Infinity Group.

quantum effect which screens the energy by as much as 95.5% in full agreement with measurements. In particular we will show that the ratio of the two Betti numbers [9-12] fixes the homology of space-time’s de Rham topology of smooth classical space-time of relativity and the rugged K3 Kähler [11] based quantum space-time of quantum gravity and give us a scaling λQR = b2 (smooth)/ b2 (Kähler) which accounts for the 95.5% missing dark energy [4]. It is well known that the Betti numbers are topological invariants of a manifold [9,10] exactly as the dimensions and the Euler characteristics [9-12] with the added advantage that b2 counts what we may call three dimensional holes (voids) [9] in the manifold (space-time fabric). That way all the fine structures of our space are taken into account [9,13]. How this actually is done is what we will explain next.
3. Homology of a Space-Time Based on Crisp K3 Kähler Manifold
Following super strings and related theories [12] we look first at the possibility of a quantum gravity space-time based upon a K3 Kähler manifold [13]. We start with a non-fuzzy crisp Kähler then look at the fractal-like fuzzy case.
3.1. Classical Non-Fuzzy Kähler
We consider a K3 Kähler manifold with four complex dimensions used extensively in theories with hidden dimensions particularly super and Heterotic string theory [12,13]. The manifold is fixed by the Betti numbers which determine the Euler characteristic and the signature. In case of non-fuzzy (crisp) K3 the Betti numbers are [10,13]
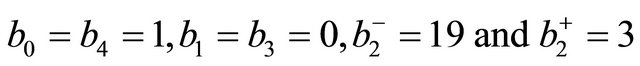 . (1)
. (1)
It follows then that the Euler characteristic is [10,13]
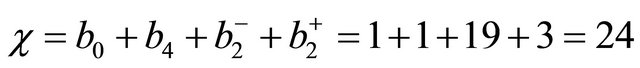 (2)
(2)
while [10,13]
 (3)
(3)
and the signature is [10,13]
 (4)
(4)
We stress once more that b2 counts the 3 dimensional holes in K3 and will play a crucial role in our derivation.
3.2. Fuzzy, Fractal-Like K3 Kähler
Now we look at an even more exotic version of K3 [13]. With that we mean El Naschie’s fuzzy Kähler which he used in earlier studies in a slightly modified form [13, 14]. The El Naschie Kähler we construct here is a fuzzy version of the one considered above. The Kähler in question is given by the same  and b3 as the previous crisp Kähler. Only
and b3 as the previous crisp Kähler. Only  and
and  which measure a sort of average number of 3D fractal voids are given by [13,14]
which measure a sort of average number of 3D fractal voids are given by [13,14]
 and
and  (5)
(5)
where . It follows then that [13,14]
. It follows then that [13,14]
 . (6)
. (6)
It is important to note the following: The small numbers  = 0.05572809014 as well as
= 0.05572809014 as well as  = 0.236067977 and
= 0.236067977 and 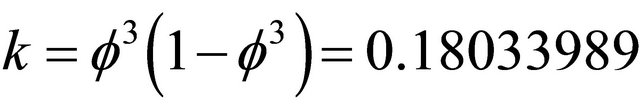 all have various physiccal, topological and geometrical interpretations. For instance
all have various physiccal, topological and geometrical interpretations. For instance  is the exact value of the vital Immirzi parameter of loop quantum gravity without which nothing would fit in this theory [15]. In addition and as realized for the first time by El Naschie
is the exact value of the vital Immirzi parameter of loop quantum gravity without which nothing would fit in this theory [15]. In addition and as realized for the first time by El Naschie  may be viewed as the probability for quantum entanglement of three quantum particles while
may be viewed as the probability for quantum entanglement of three quantum particles while  is the well known Hardy’s generic probability of quantum entanglement [16,17] for two particles which was also confirmed experimentally. The
is the well known Hardy’s generic probability of quantum entanglement [16,17] for two particles which was also confirmed experimentally. The  on the other hand is the generic probability of a Cantorian space-time with a core Hausdorff dimension equal to
on the other hand is the generic probability of a Cantorian space-time with a core Hausdorff dimension equal to  and is directly related to the famous Unruh temperature as demonstrated by El Naschie in some of his unpublished papers and lectures. Finally
and is directly related to the famous Unruh temperature as demonstrated by El Naschie in some of his unpublished papers and lectures. Finally
 (7)
(7)
That means
 , (8)
, (8)
which is a deep and useful relation utilized in various E-Infinity derivations.
4. Elevating Einstein’s Relativistic Equation to a Quantum Gravity Energy-Mass Relation
We said that b2 is an important homological invariant of a manifold [9-11] and that it basically counts the 3 dimensional voids in the manifold [9,14]. For a two sphere S2 or any connected manifold b2 is equal to unity b2 = 1. On the other hand for our classical Kähler b2 = 3 + 19 = 22, and this number already indicates that this manifold is almost a Swiss cheese full of 3 dimensional holes [10, 13]. Compared to the smooth S2 manifold akin to the space-time of Einstein, K3 has 22 times less space-time and following general relativity, less energy. Now following, for instance, Nottale’s scale relativity principle, we could define a scaling λQR to be:
 (9)
(9)
and use it to scale E = m0c2 to
 (10)
(10)
This implies that the missing hypothetical dark energy is
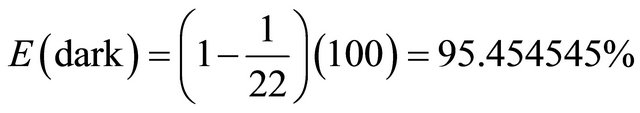 . (11)
. (11)
This is extremely close to the cosmological measurement [4]. Even better still, if we use the fuzzy version we arrive at a mathematically exact equation
 . (12)
. (12)
In fact when using the fuzzy Kähler we notice immediately a quantum mechanical interpretation of the result because
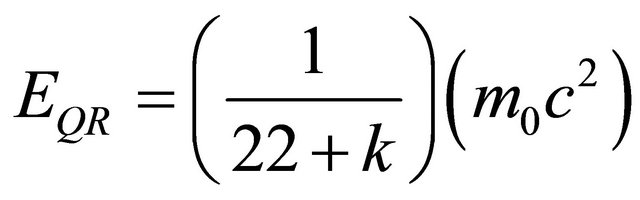 (13)
(13)
means that
 (14)
(14)
However  is nothing else but Hardy’s generic quantum entanglement [16,17] so that our λQR may be viewed as the screening of a substantial part of the energy in the cosmos by quantum entanglement reducing the Newtonian action at distance by as much as
is nothing else but Hardy’s generic quantum entanglement [16,17] so that our λQR may be viewed as the screening of a substantial part of the energy in the cosmos by quantum entanglement reducing the Newtonian action at distance by as much as  95.4915%. Finally there is an even more immediate interpretation when we invoke string theory and M-theory. The largest number of dimensions in Heterotic string theory is 26 in the classical case [12] and 26 + k in the transfinite fractal-fuzzy case [7,14]. However we can make real measurement only via 4 dimensions, 3 space dimensions and one time dimension. Thus we have 22 hidden dimensions [12]
95.4915%. Finally there is an even more immediate interpretation when we invoke string theory and M-theory. The largest number of dimensions in Heterotic string theory is 26 in the classical case [12] and 26 + k in the transfinite fractal-fuzzy case [7,14]. However we can make real measurement only via 4 dimensions, 3 space dimensions and one time dimension. Thus we have 22 hidden dimensions [12]
 (15)
(15)
or more accurately [12,14]
 (16)
(16)
Thus our scaling exponent is
 (17)
(17)
or in the fuzzy case [13,14]
 (18)
(18)
Within this mental picture we could say that the missing dark energy is concealed and hidden inside the dark extra dimension [7,12,14]. It is a deep philosophical and ontological question to consider something which we cannot measure nor detect to be real or not.
5. Conclusion
The homology of K3 Kähler and what El Naschie calls extra “dark” dimensions is the definite cause behind what we call the missing dark energy [4]. To arrive at the correct quantitative result and reconcile theory with experiments we need to scale the classical E = m0c2 by a scale relativity factor λQR defined as the ratio of two second Betti numbers [10,11]. Since the Betti number of fuzzy Kähler b2 is 22 + k and since b2 = 1 for Einstein space of special relativity, our λQR becomes equal to 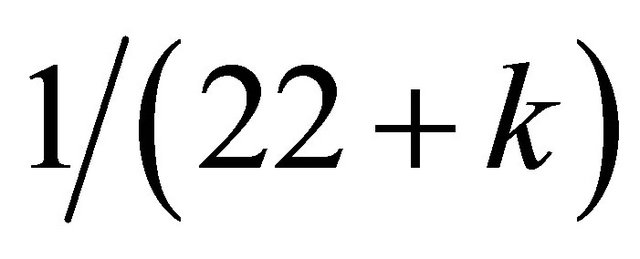 and one finds
and one finds  [9]. This means the so-called missing dark energy of the cosmos is exactly equal to
[9]. This means the so-called missing dark energy of the cosmos is exactly equal to . It is almost surreal how close the results of cosmic measurement are to this percentage [4]. Noting that λQR may also be written as
. It is almost surreal how close the results of cosmic measurement are to this percentage [4]. Noting that λQR may also be written as  that means half Hardy’s quantum entanglement probability found using orthodox quantum mechanics and confirmed through sophisticated quantum information experiments, we feel that the ordinary sharp non-fuzzy K3 Kähler manifold approximates quantum gravity space-time geometry and topology to an astonishing extend and must be real. Seen that way, we must infer with El Naschie that the designer of the universe is a mathematician [1] with a deep inclination towards topology, geometry and number theory [7]. From a purely intuitive view point however the result is not surprising when we remember that in terms of particle physics Einstein’s special relativity could in principle be found from a Lagrangian with a single generalized coordinate, namely the photon. A realistic theory of nature however must have a Lagrangian with a minimum of 12 generalized coordinates representing 12 massless gauge Bosons being the number of messenger particles of the standard model of high energy physics [1,7,14]. Our E-Infinity team has checked El Naschie’s result using at least 10 different theories including Nottale’s scale relativity, Magueijo and Smolin’s varying speed of light theory, Witten’s M-theory, Veneziano’s dual resonance theory and quantum field Yang-Mills theory in curved space-time and obtained exactly the same result reported [18,19]. Table 1 gives an overview of some of these results. With that we feel quite confident that the mystery of the dark energy has been solved at least in principle by Mohamed El Naschie and that it is essentially not a mystery any more.
that means half Hardy’s quantum entanglement probability found using orthodox quantum mechanics and confirmed through sophisticated quantum information experiments, we feel that the ordinary sharp non-fuzzy K3 Kähler manifold approximates quantum gravity space-time geometry and topology to an astonishing extend and must be real. Seen that way, we must infer with El Naschie that the designer of the universe is a mathematician [1] with a deep inclination towards topology, geometry and number theory [7]. From a purely intuitive view point however the result is not surprising when we remember that in terms of particle physics Einstein’s special relativity could in principle be found from a Lagrangian with a single generalized coordinate, namely the photon. A realistic theory of nature however must have a Lagrangian with a minimum of 12 generalized coordinates representing 12 massless gauge Bosons being the number of messenger particles of the standard model of high energy physics [1,7,14]. Our E-Infinity team has checked El Naschie’s result using at least 10 different theories including Nottale’s scale relativity, Magueijo and Smolin’s varying speed of light theory, Witten’s M-theory, Veneziano’s dual resonance theory and quantum field Yang-Mills theory in curved space-time and obtained exactly the same result reported [18,19]. Table 1 gives an overview of some of these results. With that we feel quite confident that the mystery of the dark energy has been solved at least in principle by Mohamed El Naschie and that it is essentially not a mystery any more.
NOTES