1. Introduction
We have formulated in the language of the D-modules and their sheaves, like the given in a resolution [APM] 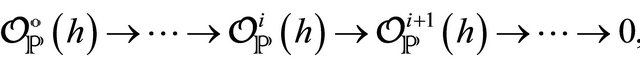 the correspondence between the space of coherent D-modules and the space of equations of massless fields
the correspondence between the space of coherent D-modules and the space of equations of massless fields  which can be established if we can grantee the uniqueness of the Penrose transform. This at least, have stayed guarantied of a partial form to conformal class obtained by the classical Penrose transform [4]
which can be established if we can grantee the uniqueness of the Penrose transform. This at least, have stayed guarantied of a partial form to conformal class obtained by the classical Penrose transform [4]
 (1)
(1)
that in the  modules categories, and to the functors
modules categories, and to the functors 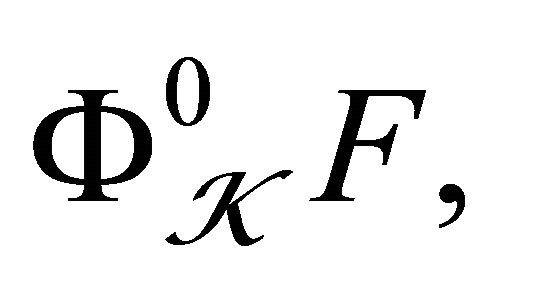 and
and  is translated in
is translated in
 (2)
(2)
where  is the full subcategory of
is the full subcategory of  whose open sets are of the
whose open sets are of the  type to some bundle of lines L.
type to some bundle of lines L.
Precisely these equivalences shape a classification given of the homogeneous vector bundles of lines [2,5] to differential operator classification [1].
Some important facts that demonstrate by means of the use of the Radon transform and their version of  Module transform (Radon-Schmid transform), is the necessity of include a result that establishes the regularity in the analytical sense of the Riemannian manifold, which shapes the space-time, and that allows the application of the involutive distribution theorem on integral submanifolds as solutions of the corresponding equations of massless fields on submanifolds isomorphic in the Kählerian model inside of the Flat model given on
Module transform (Radon-Schmid transform), is the necessity of include a result that establishes the regularity in the analytical sense of the Riemannian manifold, which shapes the space-time, and that allows the application of the involutive distribution theorem on integral submanifolds as solutions of the corresponding equations of massless fields on submanifolds isomorphic in the Kählerian model inside of the Flat model given on 
Of fact, an analogy in the obtaining of models of space-time (under the same reasoning) must be realized between special Lagrangian submanifolds and m-folds of Calabi-Yau. But to it, we need define the complex microlocal structure that define all the phenomena of strings and branes in microscopic level, which happen in the 6-dimensional component of the universe (6-dimensional compact Riemannian manifold) with ratio of the order 10−33 cm (Max Plank longitude of a string) [1,6]. The Penrose transform is an integral geometric method that interprets elements of various analytic cohomology groups on open subsets of complex projective 3-space as solutions of linear differential equations on the Grassmannian of 2-planes in the 4-space. The motivation for such transform comes from the interpretation of this Grassmannian as the complexification of the conformal compactification of the Minkowski space and their differential equations being the massless field equations of various helicities .
.
Nevertheless: what is the global notion of the equivalence created through the Radon-Schmid transform for the general case of classes not necessary conformal? Which are the classes that are extensions of the space of equivalences of the type (1)? Why are necessary these classes to include more phenomena of the space-time? What version of the Penrose transform will be required?
Part of the goal of our research is centered in the extension of the space of equivalences of the type (1), under a more general context given through the language of the D-modules, that is to say, we want extend our research al context of non-conformal manifolds and with it to find some condition at least of sufficiency for the resolution via the generalized Penrose transform of  Modules, which are
Modules, which are 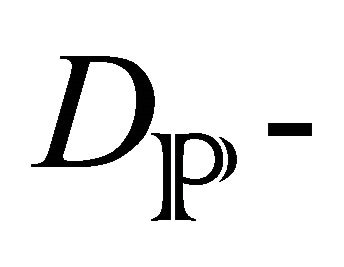 Modules and to induce their application to para-conformal classes through of the use of versions more generalized of Radon transforms that are connected with Penrose transforms to create conformal invariance in geometrical images that are physical stacks at least in the first development and tries to obtain an integral operators cohomology that be a sheaf cohomology group that includes the BRST-cohomology studied in field theory and where be applicable the second scheme of gauge theories (topological gauge theory [7]). The topological gauge theory search use the deformation theory in derived sheaves that not requires use excessive functor calculations. In this sense, the most direct and shortest applications of deformation theory are to the study of moduli spaces (remember that we want to obtain equivalences between categories of objects that are D-modules in different scales inside of field theory from a point of view of bundle of lines, worldsheets from
Modules and to induce their application to para-conformal classes through of the use of versions more generalized of Radon transforms that are connected with Penrose transforms to create conformal invariance in geometrical images that are physical stacks at least in the first development and tries to obtain an integral operators cohomology that be a sheaf cohomology group that includes the BRST-cohomology studied in field theory and where be applicable the second scheme of gauge theories (topological gauge theory [7]). The topological gauge theory search use the deformation theory in derived sheaves that not requires use excessive functor calculations. In this sense, the most direct and shortest applications of deformation theory are to the study of moduli spaces (remember that we want to obtain equivalences between categories of objects that are D-modules in different scales inside of field theory from a point of view of bundle of lines, worldsheets from  and all space time
and all space time  (for example D-branes and strings)). If we have a pre-deformation functor
(for example D-branes and strings)). If we have a pre-deformation functor , obtained from a point x, of a moduli space
, obtained from a point x, of a moduli space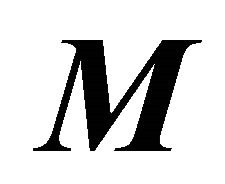 , then as was mentioned in [8,9], the notions of tangent space and formal smoothness for
, then as was mentioned in [8,9], the notions of tangent space and formal smoothness for , and for
, and for , coincide. Noting that if a manifold is smooth, their dimension is the dimension of their tangent space, one could prove in this way that the Grassmannian
, coincide. Noting that if a manifold is smooth, their dimension is the dimension of their tangent space, one could prove in this way that the Grassmannian 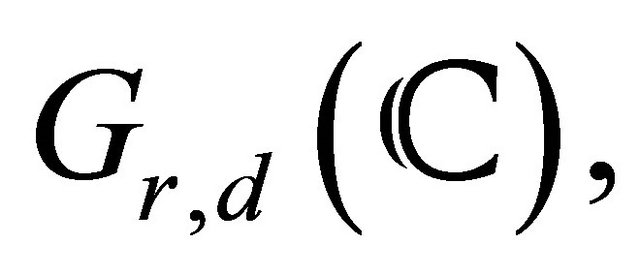 is smooth of dimension
is smooth of dimension  although of course a proof of representability gave inside of the deformation theory a more direct and stronger statement in showing that it is covered by copies of
although of course a proof of representability gave inside of the deformation theory a more direct and stronger statement in showing that it is covered by copies of  However, later we will study other fine moduli spaces, such as Hilbert spaces, where in many cases deformation theory is the only way of obtaining such statements. Along these lines, one of the archetypical examples is the moduli space
However, later we will study other fine moduli spaces, such as Hilbert spaces, where in many cases deformation theory is the only way of obtaining such statements. Along these lines, one of the archetypical examples is the moduli space  of curves of genus g, which is proposed inside of moduli spaces that appear in the Fukaya category Fuk
of curves of genus g, which is proposed inside of moduli spaces that appear in the Fukaya category Fuk  [14]. This parametrizes flat families of smooth, proper, geometrically connected curves of genus g. Although it is not representable, it is nonetheless rather well-behaved for
[14]. This parametrizes flat families of smooth, proper, geometrically connected curves of genus g. Although it is not representable, it is nonetheless rather well-behaved for 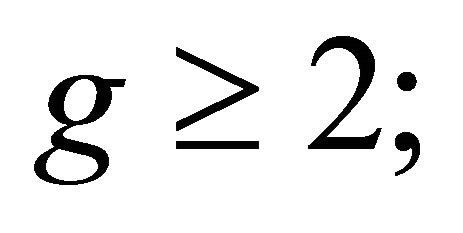 technically, it is a “DeligneMumford stack”, but from our point of view, it suffices to take for granted that the notions of smoothness and dimension can be defined independently, and in this sense there are many results, proved via deformation theory [8,10].
technically, it is a “DeligneMumford stack”, but from our point of view, it suffices to take for granted that the notions of smoothness and dimension can be defined independently, and in this sense there are many results, proved via deformation theory [8,10].
Until this point, can establish a correspondence of the genus as geometric images with elements of field theory? Can a space-time carpet be created from the strings tacked and D-branes, like 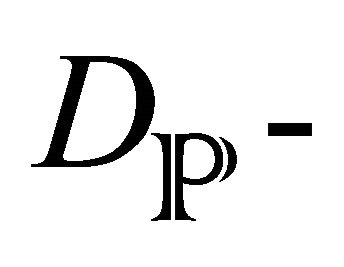 modules to the creation of
modules to the creation of  modules that cover all
modules that cover all ? Which must be these
? Which must be these  -modules? Are there some space of geometric invariant equivalences that that is adapted to the whole standard model of the space-time, doing that derived categories are applicable to the SUSY theory and QFT theory of same form, that is to say, to a transitive class of moduli spaces in the space
-modules? Are there some space of geometric invariant equivalences that that is adapted to the whole standard model of the space-time, doing that derived categories are applicable to the SUSY theory and QFT theory of same form, that is to say, to a transitive class of moduli spaces in the space ?
?
These and many other aspects can be answered if we generalize functors between categories of coherent DModules in equivariant D-modules to sub-clases of the homogeneous space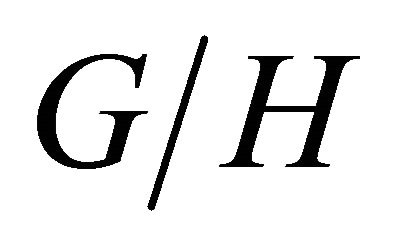 , of G-equivariant D-modules, where the functors of the transform of D-modules are the obtained through the Penrose-Radon transform with close range on D-modules that are certain generalized g-modules [13,28], in the context of the infinite Lie theory, and must be Harish-Chandra functores of derived categories [20], in these modules. This latter functorial application must record in eigen-sheaves de categorías de Hecke.
, of G-equivariant D-modules, where the functors of the transform of D-modules are the obtained through the Penrose-Radon transform with close range on D-modules that are certain generalized g-modules [13,28], in the context of the infinite Lie theory, and must be Harish-Chandra functores of derived categories [20], in these modules. This latter functorial application must record in eigen-sheaves de categorías de Hecke.
2. Revisited Cycles and Equivalences (in the Mirror Symmetry)
Now in the context of the generalized D-modules (inside of the derived categories) to the use of the Schmid-Radon transform, and finally obtain Radon-Penrose Transform, the functor [2]
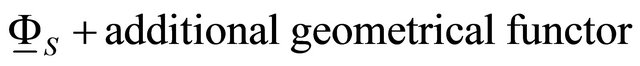 (3)
(3)
establish a equivalence between the category M(DX- modules/flat connection), and M(DY-modules/Singularies to along of the involutive manifold V/flat connection) [4,11]. Then our moduli space that we constructed is the categorization of equivalences:
 (4)
(4)
considering the moduli space as base [4],
 (5)
(5)
The moduli space (5) and under certain hypothesis of the twisted (0, 2)-sigma model whose path integral lolizes on holomorphic maps to twistor space [23], is the corresponding flat moduli space
 [6], which satisfies under speal conditions of compactication that (considering the formula to helicities when there is holes of genus
[6], which satisfies under speal conditions of compactication that (considering the formula to helicities when there is holes of genus  in a Kähler manifold
in a Kähler manifold ,
,
 (6)
(6)
then the cohomology on moduli spaces is the cohomology of the space-time with an equivalence like the given in (1), to a more general cohomological group that the given by  and whose dimension of
and whose dimension of  can be calculated by the intersection methods, to a complex sheaf O [23], which is of the type
can be calculated by the intersection methods, to a complex sheaf O [23], which is of the type 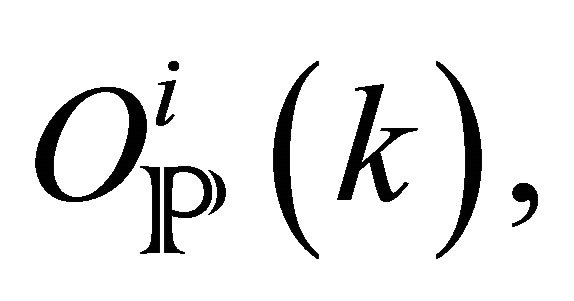 (for example: elements of the cohomology group
(for example: elements of the cohomology group  ,1 correspond via the Penrose transform to the spacetime fields of helicity h, so that in particular a negative helicity gluon corresponds to a twistor wavefunction of weight 0. The additional geometrical hypothesis in the functor (3), comes established by the geometrical duality of Langlands [5], which says that the derived category of coherent sheaves on a moduli space
,1 correspond via the Penrose transform to the spacetime fields of helicity h, so that in particular a negative helicity gluon corresponds to a twistor wavefunction of weight 0. The additional geometrical hypothesis in the functor (3), comes established by the geometrical duality of Langlands [5], which says that the derived category of coherent sheaves on a moduli space  where C, is the complex given by
where C, is the complex given by
 (7)
(7)
which is equivalent to the derived category of D-modules on the moduli space of holomorphic vector G-bundles given by  [6]. These equivalences permit to map points of
[6]. These equivalences permit to map points of  to eigen-sheaf of Hecke given by
to eigen-sheaf of Hecke given by  [23]. The complex
[23]. The complex 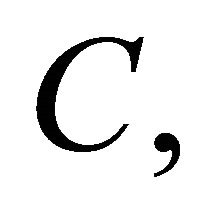 is an infinite dimensional
is an infinite dimensional  -complex. Then we need to establish a local cohomology to coherent D-modules
-complex. Then we need to establish a local cohomology to coherent D-modules , to every reduce analytic subspace of
, to every reduce analytic subspace of . In other words, to find the local cohomology that is intrinsic part of the cohomology of (7). We will do the following extension of
. In other words, to find the local cohomology that is intrinsic part of the cohomology of (7). We will do the following extension of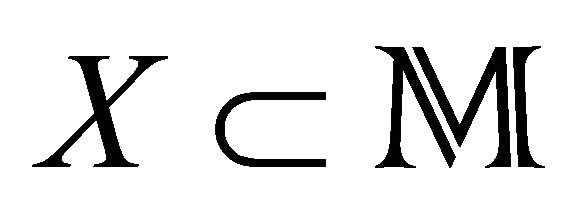 .
.
Considering the filtration  of closed subspaces of a Riemannian complex manifold M, which defines the topology of
of closed subspaces of a Riemannian complex manifold M, which defines the topology of . Exactly like an open covering of
. Exactly like an open covering of , this filtration associates to every sheaf
, this filtration associates to every sheaf  their Cěch complex, where the filtration persists associating to every sheaf a Cousin complex
their Cěch complex, where the filtration persists associating to every sheaf a Cousin complex  The required cohomology is on
The required cohomology is on  This cohomology is on sheaves of
This cohomology is on sheaves of  modules that are
modules that are  modules. The
modules. The  -modules there must be the given in the category of (4), with the due meromorphic extensions of one Cousin-Dolbeault-complex to the inclusion of involutive manifolds with singularities [16].
-modules there must be the given in the category of (4), with the due meromorphic extensions of one Cousin-Dolbeault-complex to the inclusion of involutive manifolds with singularities [16].
We consider the following fundamental results to the securing of the Hecke sheaves using local cohomology in the Cousin-Dolbeault-complex.
Theorem 2.1. 1) The local algebraic cohomology is a complex with D-holonomic cohomology; 2) We have the canonical morphism in 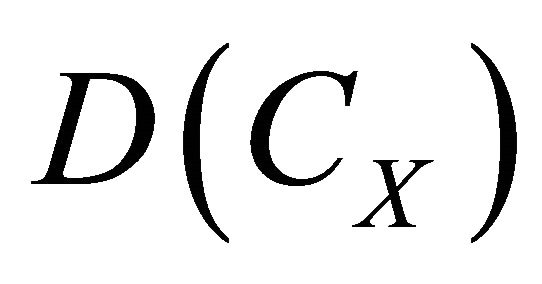
 (8)
(8)
Proof. [24].
By the kashiwara theorem, we have that the equivalence between the categories , and
, and  preserves coherency and holonomicity [3]. Then preserve conformability in
preserves coherency and holonomicity [3]. Then preserve conformability in  [12,13].
[12,13].
In this case we want to decompose singular regions 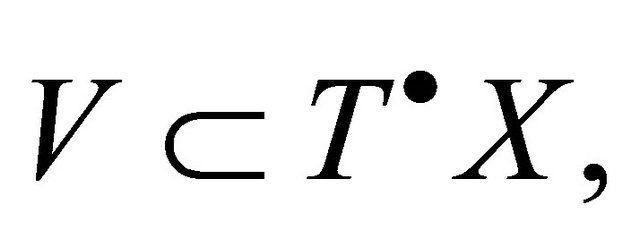 of the space-time
of the space-time , in regions of conformal nature that could be valued through contour integrals, whose cohomology of contours could be related to the cohomology of the total Riemannian complex manifold maintaining the conformability of these micro-components. Then for micro-local analysis, we can observe flatness conditions of the space to scales of the
, in regions of conformal nature that could be valued through contour integrals, whose cohomology of contours could be related to the cohomology of the total Riemannian complex manifold maintaining the conformability of these micro-components. Then for micro-local analysis, we can observe flatness conditions of the space to scales of the  and the singularities that shape
and the singularities that shape  there are zeros of polynomials of algebraic manifold of the Riemannian complex variety.
there are zeros of polynomials of algebraic manifold of the Riemannian complex variety.
In case of the Cousin complexes, the idea is to decompose a complex with non-conformal properties in conformal parts where it exists flatness due to the holonomicity and conformability of , to these scales. A promissory result in this sense is the due to Kashiwara applying jointly the Poincarè theorem (Theorem 2.1) in local cohomology, where for the resolution proposed in [13], we can investigate in the cohomology of
, to these scales. A promissory result in this sense is the due to Kashiwara applying jointly the Poincarè theorem (Theorem 2.1) in local cohomology, where for the resolution proposed in [13], we can investigate in the cohomology of  through the moduli space
through the moduli space 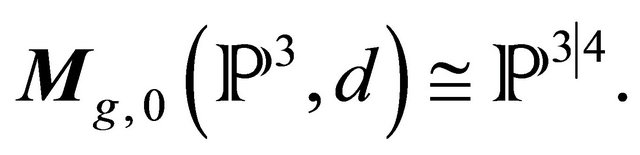
Then from the depth and substantial of the complex (7) the conformability is maintained by the Cousin complexes that shape quotients of complexes to every component of the complex (7). The natural morphism
 (9)
(9)
induces a morphism in  that is to say,
that is to say,
 (10)
(10)
Theorem 2.2. The morphism (*) is an isomorphism in and the local cohomology sheaves of Y, are  -holonomic and admissible modules.
-holonomic and admissible modules.
Proof. [21,24]. □
To relate the cohomological groups of the sheaves of  with the sheaves of
with the sheaves of  we use an intertwining operator that compound with the Penrose transform, allows determine the solution space of the differential equations of the operators given for the equivalence of the moduli space (4). In the following section we will use like intertwining operator the twistor transform, which establishes an isomorphism of Harish-Chandra modules.
we use an intertwining operator that compound with the Penrose transform, allows determine the solution space of the differential equations of the operators given for the equivalence of the moduli space (4). In the following section we will use like intertwining operator the twistor transform, which establishes an isomorphism of Harish-Chandra modules.
Then our sheaves complex takes the form as a holomorphic bundles complex and is aquanstance as to this can be associated branes. In this case we associate branes to every possible sheaf: we can map branes to sheaves but the reciprocal thing is not true.
3. Methods: Equivalences of Cycles in Quasi-G-Equivariant D-Modules Category and Their Ramifications in Derived Sheaves
To obtain a generalization of the Kashiwara theorem in the context of the G-equivariant D-modules is necessary the geometric Zuckerman functor. This is the localization of the equivariant Zuckerman functor to the derived equivariant  categories on generalized flag varieties (this to apply in our study an appropriate D-module transform of the Penrose transform type). To this case, we define our categories of interest and construct the geometric Zuckerman functor from the basic D-module functors.
categories on generalized flag varieties (this to apply in our study an appropriate D-module transform of the Penrose transform type). To this case, we define our categories of interest and construct the geometric Zuckerman functor from the basic D-module functors.
The category of (left) G-equivariant 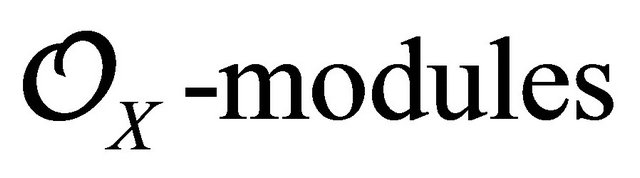 is denoted by
is denoted by  The following theorem is well known:
The following theorem is well known:
Theorem 3.1. If  acts on
acts on  freely, there is an equivalence of categories
freely, there is an equivalence of categories 
For homogeneous spaces, we can make a stronger statement. Let  be a complex linear group, let
be a complex linear group, let 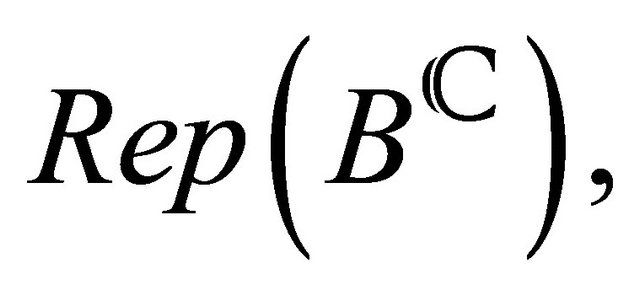 be the category of algebraic representations of
be the category of algebraic representations of 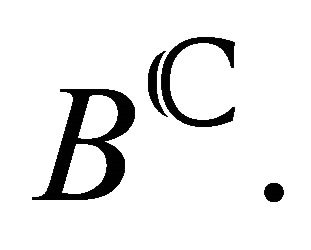
Proof. [20]. □
Theorem 3.2. If 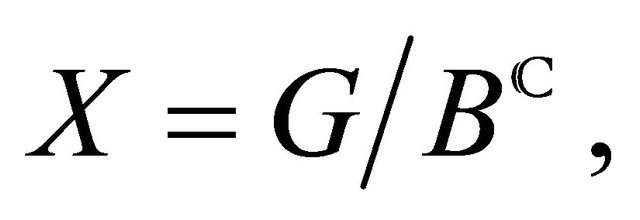 there is an equivalence of categories
there is an equivalence of categories 
Proof. [20]. □
We consider the Penrose transform between flag manifolds on an algebraic complex group  using the Kashiwara theorem between quasi-
using the Kashiwara theorem between quasi-  - modules and some kind representation spaces, which are
- modules and some kind representation spaces, which are  (complex vector space endowed always with an action of a Lie algebra
(complex vector space endowed always with an action of a Lie algebra  associated to
associated to  and an action
and an action which is compatible in some sense when
which is compatible in some sense when  is a closed algebraic subgroup of
is a closed algebraic subgroup of ).
).
Let  be a quasi-
be a quasi- -module belonging to the subcategory of
-module belonging to the subcategory of  -modules given by
-modules given by  (category of the
(category of the  - modules).
- modules).
The idea is to obtain equivalence between the different classes of -modules establishing the isomorphism between the categories
-modules establishing the isomorphism between the categories  and
and  where
where must be the functor of Zuckerman restricted to the subcategory of left
must be the functor of Zuckerman restricted to the subcategory of left  -modules to obtain the derived category that is a product of a trianguled subcategory (like the given in [1,6]) for a factor category that determine us the functor of Harish-Chandra between categories. These equivalences in analogy to established in (4) take the form for specific
-modules to obtain the derived category that is a product of a trianguled subcategory (like the given in [1,6]) for a factor category that determine us the functor of Harish-Chandra between categories. These equivalences in analogy to established in (4) take the form for specific  -modules
-modules
 (11)
(11)
considering the moduli space as base,
 (12)
(12)
where  such that
such that  where
where  and
and  are Higgs fields on either side of the open string [23]. This condition established in the kernel of equivalences inside the moduli space
are Higgs fields on either side of the open string [23]. This condition established in the kernel of equivalences inside the moduli space  is analogous to the given by the isomorphism of the Penrose transform discussed in foot of page 2, in the section 2, in this work. The idea is extend the harmonic condition to the functions to differential operators of derived sheaves that are in
is analogous to the given by the isomorphism of the Penrose transform discussed in foot of page 2, in the section 2, in this work. The idea is extend the harmonic condition to the functions to differential operators of derived sheaves that are in  cohomology, such that the equivalences in (5) are defined by the certain functors due to the duality between the
cohomology, such that the equivalences in (5) are defined by the certain functors due to the duality between the  resolution and meromorphic version of the Cousin complex2 associated to
resolution and meromorphic version of the Cousin complex2 associated to 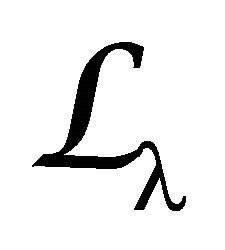 (bundle of lines associated to the flag manifold
(bundle of lines associated to the flag manifold  then
then 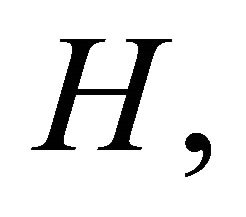 is a Borel subgroup).
is a Borel subgroup).
Let 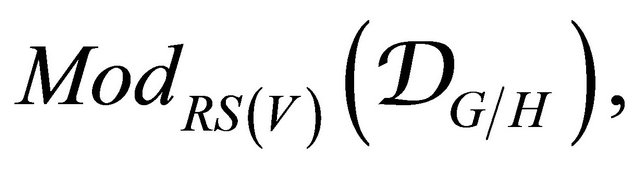 be the thick subcategory of
be the thick subcategory of 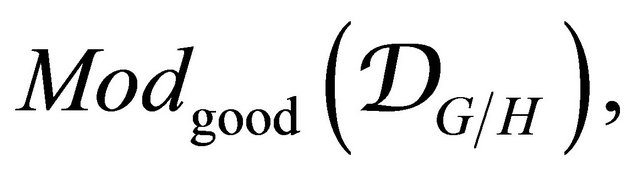 whose objects have regular singularities on
whose objects have regular singularities on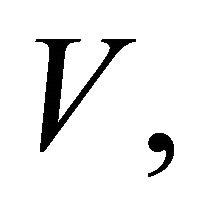 and by
and by  the full triangulated subcategory of
the full triangulated subcategory of 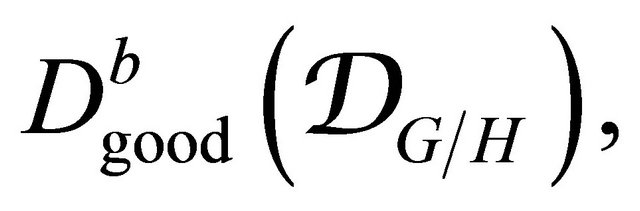 whose objects have cohomology groups belonging to
whose objects have cohomology groups belonging to  [6]:
[6]:
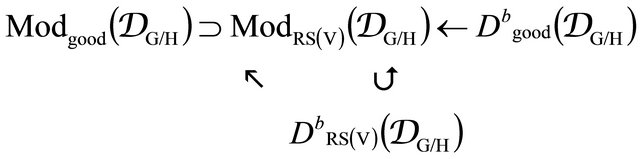
Let  be a Harish-Chandrs pair, let
be a Harish-Chandrs pair, let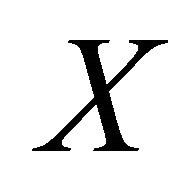 , be a generalized flag variety for
, be a generalized flag variety for  and let
and let  be a homogeneous twisted sheaf of differential operators on
be a homogeneous twisted sheaf of differential operators on 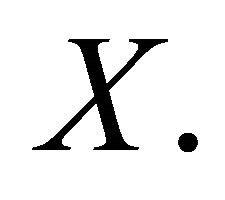 A weak Harish-Chandra sheaf for the pair
A weak Harish-Chandra sheaf for the pair  is a quasi-coherent
is a quasi-coherent  with a
with a  structure such that the action of
structure such that the action of  is
is  A weak Harish-Chandra sheaf is a Harish-Chandra sheaf if additionally the differential of the
A weak Harish-Chandra sheaf is a Harish-Chandra sheaf if additionally the differential of the  agrees with the action of
agrees with the action of  induced by
induced by 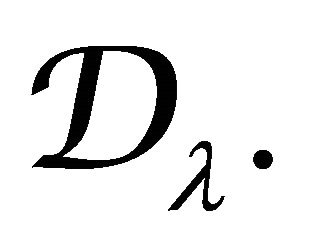
A morphism of weak Harish-Chandra sheaves is a  homomorphism which respects the underlying
homomorphism which respects the underlying  As with weakly equivariant Harish-Chandra modules, we will use
As with weakly equivariant Harish-Chandra modules, we will use 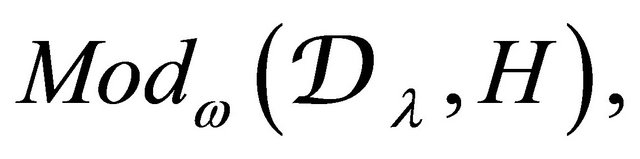 to denote the category of weak Harish-Chandra sheaves and
to denote the category of weak Harish-Chandra sheaves and  for the category of Harish-Chandra sheaves. There is an equivalence of categories for
for the category of Harish-Chandra sheaves. There is an equivalence of categories for  anti-dominant and regular
anti-dominant and regular
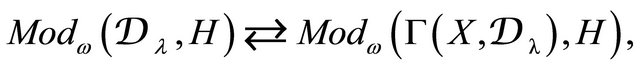 (13)
(13)
We construct the derived equivariant Harish-Chandra sheaf category in the same way as the derived equivariant Harish-Chandra module category. The derived equivariant Harish-Chandra module category is precisely that we want obtain to consider it inside the base moduli space to determine an extension of this one, in the context of a cousin cohomology.
Theorem 3.3. The morphism (sfc) is an isomorphism in and the local cohomology sheaves of  are
are  - holonomic and admissible modules.
- holonomic and admissible modules.
Proof. [24]. □
Here the local system on the complex manifold is given by the  inside one Dolbeault-Cousin cohomology that shape a complex as the given in the Morphism (9).
inside one Dolbeault-Cousin cohomology that shape a complex as the given in the Morphism (9).
Theorem (Deligne) 3.4. The functor  gives a categorical equivalence between the category of regular connections on an algebraic manifold
gives a categorical equivalence between the category of regular connections on an algebraic manifold  and that of local systems on the complex manifold
and that of local systems on the complex manifold 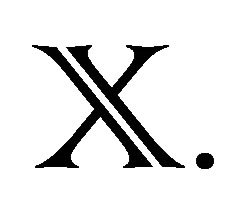
Proof. [15]. □
4. Results
Theorem 4.1 (F. Bulnes). The derived category of quasiG-equivariant  modules can be identify for twisted Hecke category if
modules can be identify for twisted Hecke category if  is a derived version of the category of Harish-Chandra to a certain
is a derived version of the category of Harish-Chandra to a certain 
Proof. If  then
then  of the group
of the group 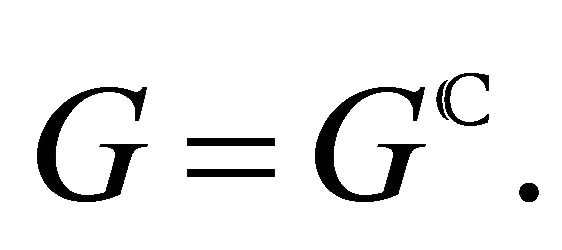 b-equivariant D-module on the flag manifold
b-equivariant D-module on the flag manifold  provide integral kernels and thus integral transforms, to know
provide integral kernels and thus integral transforms, to know
 3 (14)
3 (14)
For other side, realizing the following considerations to the extension of the Langlands geometrical program, the category  of D-modules is the double quotient stack of a complex reductive group
of D-modules is the double quotient stack of a complex reductive group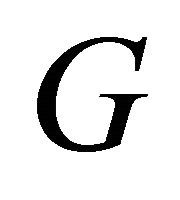 , by a Borel subgroup
, by a Borel subgroup  along with familiar related versions involving twisted D-modules. Our aim is to construct a topological field theory from
along with familiar related versions involving twisted D-modules. Our aim is to construct a topological field theory from , and in particular to relate the abelianization and center of
, and in particular to relate the abelianization and center of , to each other and in turn to character sheaves. These character sheaves are the Hecke eigensheaves required.
, to each other and in turn to character sheaves. These character sheaves are the Hecke eigensheaves required.
The Hecke category  is a fiber of a natural family of Hecke categories
is a fiber of a natural family of Hecke categories 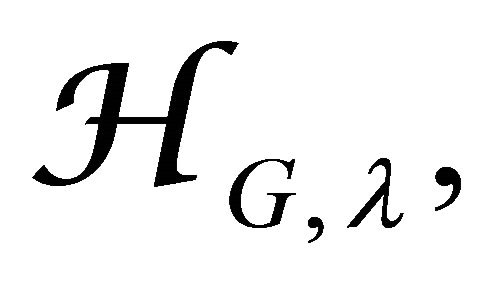 labeled by infinitesimal character
labeled by infinitesimal character  in the dual of the Cartan Lie algebra. The twisted Hecke category
in the dual of the Cartan Lie algebra. The twisted Hecke category  consists of the natural integral transforms acting on categories of
consists of the natural integral transforms acting on categories of  twisted
twisted  modules on the flag variety
modules on the flag variety 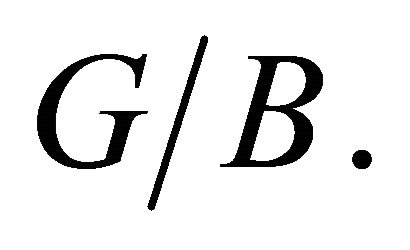 (For
(For  regular, such categories are equivalent to categories of g-modules with infinitesimal character
regular, such categories are equivalent to categories of g-modules with infinitesimal character , modulo
, modulo  (Harish-Chandra categories)). Concretely, we can realize
(Harish-Chandra categories)). Concretely, we can realize  as the monoidal category of
as the monoidal category of  modules on N\G/N with strict
modules on N\G/N with strict  monodromy with respect to the left and right actions of
monodromy with respect to the left and right actions of  (For
(For  regular, such
regular, such  modules are equivalent to Harish Chandra bi-modules for
modules are equivalent to Harish Chandra bi-modules for 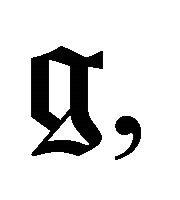 with infinitesimal character
with infinitesimal character  modulo
modulo ).
).
Taking the fibers  of the above family of Hecke categories, we can allow the parameter
of the above family of Hecke categories, we can allow the parameter  to vary infinitesimally, and obtain the monodromic Hecke categories
to vary infinitesimally, and obtain the monodromic Hecke categories  of natural integral transforms acting on categories of generalized λ-monodromic D-modules on the flag variety
of natural integral transforms acting on categories of generalized λ-monodromic D-modules on the flag variety  (For
(For  regular, such categories are equivalent to categories of
regular, such categories are equivalent to categories of  modules with generalized infinitesimal character
modules with generalized infinitesimal character  modulo
modulo ). Remember that there are basic integral transforms associated to pairs of flags in a fixed relative position indexed by an element of the Weyl group of
). Remember that there are basic integral transforms associated to pairs of flags in a fixed relative position indexed by an element of the Weyl group of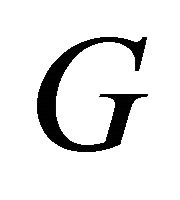 . (These are closely related to the Radon and Penrose transforms of algebraic analysis and with analogous in field theory by the twistor transform (this was established in the Gindikin conjecture [6])).
. (These are closely related to the Radon and Penrose transforms of algebraic analysis and with analogous in field theory by the twistor transform (this was established in the Gindikin conjecture [6])).
We consider a complex holomorphic bundle  on a hypersurface
on a hypersurface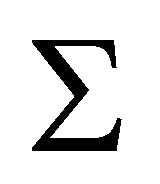 , and that is a derived category of quasi-coherent d-modules
, and that is a derived category of quasi-coherent d-modules  (that is to say, we have applied the direct Penrose transform to the bundle
(that is to say, we have applied the direct Penrose transform to the bundle  [6]) which is isomorphic to the category
[6]) which is isomorphic to the category  to some
to some 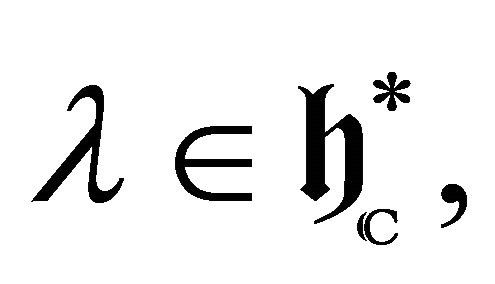 of fact,
of fact,  But for Langlands geometrical duality, whose equivalence that shape a moduli stack in the character category context, takes the form
But for Langlands geometrical duality, whose equivalence that shape a moduli stack in the character category context, takes the form
 (15)
(15)
But this means that in duality quasi-coherent versions of the affine Hecke category are images of the Penrose transfom applied to d-modules on finite flag manifolds (that is to say, in this context our d-modules are  modules). Thus
modules). Thus  and
and  lead to d-modules on finite flag varieties4.
lead to d-modules on finite flag varieties4.
| 5Using Penrose transform, we obtain the geometrical images of the vector bundles given by the category 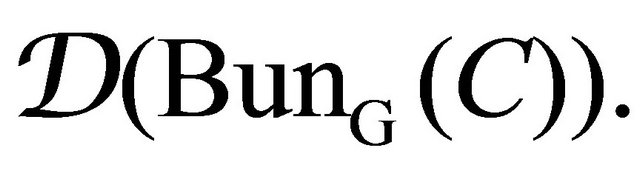 |
Newly, consider the Hecke category  Also consider
Also consider  with
with , a surface in
, a surface in . Said category assign a Riemannian surface S, the
. Said category assign a Riemannian surface S, the  category of D-modules given by
category of D-modules given by 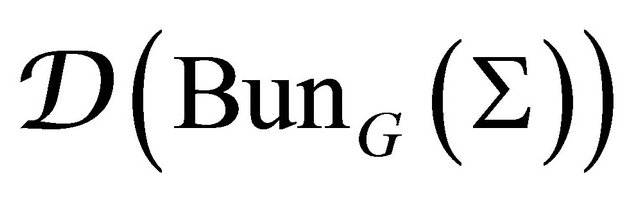 on moduli stack of G-bundles, while that
on moduli stack of G-bundles, while that  assigns the
assigns the  categories of quasi-coherent sheaves on the stack
categories of quasi-coherent sheaves on the stack  of
of  local systems of
local systems of 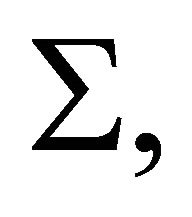 denoted also by
denoted also by  Then by the theorem given in [6], and by relative discussion to the eigen-object that stays to the apply de MO-duality [23], to A-brane on moduli space
Then by the theorem given in [6], and by relative discussion to the eigen-object that stays to the apply de MO-duality [23], to A-brane on moduli space  we have that the
we have that the  module on
module on  corresponding to a point on
corresponding to a point on  is Hecke eigen-sheaf. Then in this point, we can affirm that
is Hecke eigen-sheaf. Then in this point, we can affirm that 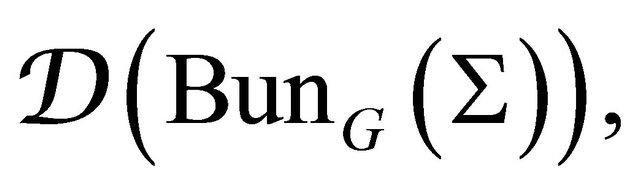 is the category of the twisted Hecke category
is the category of the twisted Hecke category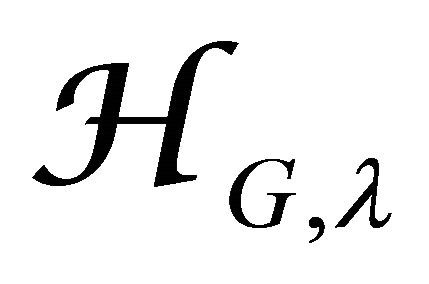 ,consists of the natural integral transforms acting on categories of
,consists of the natural integral transforms acting on categories of  twisted
twisted  modules on the flag variety
modules on the flag variety  Indeed, is necessary go from the co-cycles for the Radon-Penrose transform on
Indeed, is necessary go from the co-cycles for the Radon-Penrose transform on 
 to the obtained cycles by Penrose transform on
to the obtained cycles by Penrose transform on  and viceversa. The equivalence of both spaces of cocycles demonstrates that the functors are the given by
and viceversa. The equivalence of both spaces of cocycles demonstrates that the functors are the given by  of the moduli space
of the moduli space , which consider as base the moduli space given in (5).
, which consider as base the moduli space given in (5).
Then these functors are  invariants and their image under
invariants and their image under 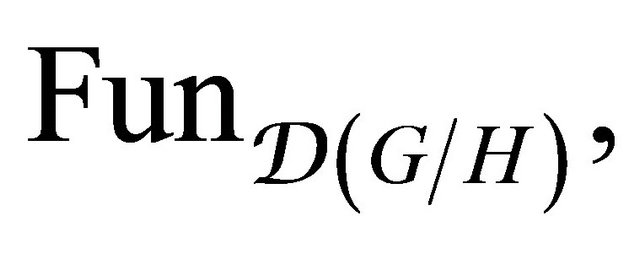 is recorded in a moduli space of holomorphic bundles
is recorded in a moduli space of holomorphic bundles  [27]5 which is an extension of the transformed cycles by the classic Penrose transform [17] The equivalence under the
[27]5 which is an extension of the transformed cycles by the classic Penrose transform [17] The equivalence under the  invariance of holomorphic bundles must be demonstrated using a generalized Penrose transform for D-modules that is the composition of an inverse image functor and a direct image functor on the side D-module, which is foreseen by the geometrical duality of Langlands [5]. □
invariance of holomorphic bundles must be demonstrated using a generalized Penrose transform for D-modules that is the composition of an inverse image functor and a direct image functor on the side D-module, which is foreseen by the geometrical duality of Langlands [5]. □
Theorem 4.2. (F. Bulnes).

being  a Cousin-Dolbeautl complex
a Cousin-Dolbeautl complex
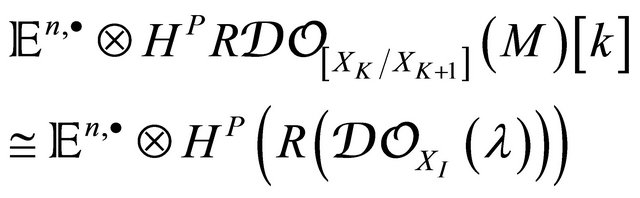
Proof. We realize an extension by local cohomology of the complexes,
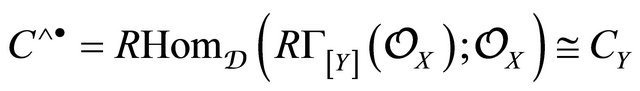 , using inverse and direct images of the Penrose transform on the corresponding Hochschild cohomologies obtained on the domains
, using inverse and direct images of the Penrose transform on the corresponding Hochschild cohomologies obtained on the domains  an
an  [6], using their developments of Dolbeault-Cousin complexes[16] The bijection of the Penrose transform on orbifolds in both cases gives the result. □
[6], using their developments of Dolbeault-Cousin complexes[16] The bijection of the Penrose transform on orbifolds in both cases gives the result. □
Corollary (F. Bulnes) 4.1. We consider the corresponding equivalence given by the Theorem 7.1. [6], and using the large resolution [1].
 (16)
(16)
we can to give the following scheme of Cousin complexes  that brings an equivalence between the spaces
that brings an equivalence between the spaces  and
and  where
where  is the supertwistor space
is the supertwistor space , in [26]. In this case, the equivalence is given by the Penrose transform on the quasi-coherent
, in [26]. In this case, the equivalence is given by the Penrose transform on the quasi-coherent  modules established by the diagram (
modules established by the diagram ( to the Verma modules diagram in the conjecture Recillas to the group
to the Verma modules diagram in the conjecture Recillas to the group  [6])
[6])
 (17)
(17)
where .
.
Proof. We consider the Cousin complex diagram

and applying to the exact succession

we find that (in the upper part)

is commutative. For other side, using the Penrose-Ward transform in the down part of the diagram we have
 [29] (18)
[29] (18)
But  in the level of moduli space
in the level of moduli space
 To obtain the equivalence between the space
To obtain the equivalence between the space
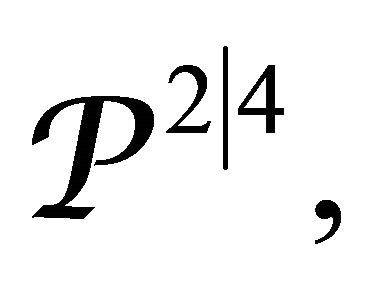 and
and  is necessary to consider the interpretation of the quadric inside the space
is necessary to consider the interpretation of the quadric inside the space 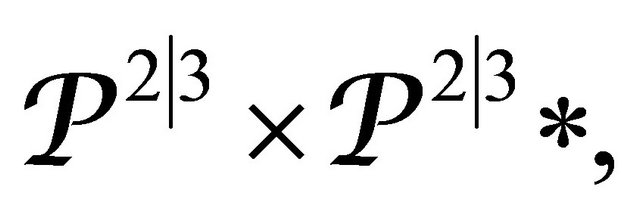 and construct the double fibration in the twistor scheme corresponding to the supertwistor space
and construct the double fibration in the twistor scheme corresponding to the supertwistor space . This double fibration takes us to
. This double fibration takes us to
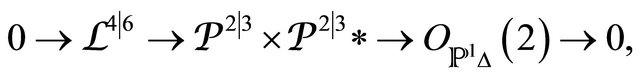 (19)
(19)
which is not vector bundles fibration. Then is necessary the degeneration of cycles given inside of  manifold signed in the equivalences of moduli spaces in the Theorem 7.1. Using action given by path integrals given in [6], we can to obtain an approximation that can legitimize the extension of the Penrose transform in the linear context (integrals become traces of matrices) of the representations in
manifold signed in the equivalences of moduli spaces in the Theorem 7.1. Using action given by path integrals given in [6], we can to obtain an approximation that can legitimize the extension of the Penrose transform in the linear context (integrals become traces of matrices) of the representations in 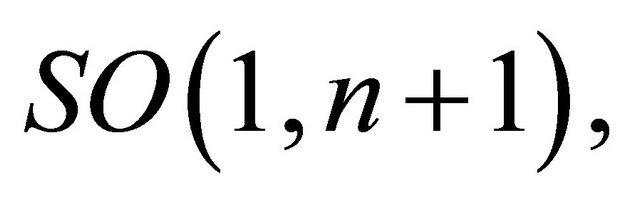 and the use of strings and heterotic strings to obtain the commutability of all diagram. Details of the calculations will happen in a next paper. □
and the use of strings and heterotic strings to obtain the commutability of all diagram. Details of the calculations will happen in a next paper. □
5. Conclusions
Spaces of equivalence modulus a relation of congruence were constructed on field solutions to establish a theory of the universe that includes the theory QFT (Quantum Field theory), the SUSY (Super-symmetry theory) and HST (heterotic string theory) using the sheaves correspondence of differential operators of the field equations and sheaves of coherent D-Modules. The above mentioned correspondence was constructed using a Zuckerman functor that is a factor of the universal functor of derived sheaves of Harish-Chandra to the Langlands geometrical program in mirror symmetry. The obtained development included complexes of D-modules of infinite dimension, generalizing this way, the BRSTcohomology in this context. With it the class of the integrable systems was extended in mathematical physics and the possibility of obtaining a general theory of integral transform for the space-time, and with it the measurement of many of their observables. Also has tends a bridge to complete a classification of the differential operators for the different field equations using on the base of Verma modules that are classification spaces of 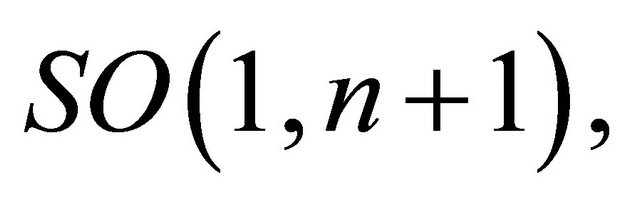 where elements of the Lie algebra
where elements of the Lie algebra  are differential operators, of the equations in mathematical physics.
are differential operators, of the equations in mathematical physics.
The cosmological problem that exists is to reduce the number of field equations that are resoluble under the same gauge field (Verma modules) and to extend the gauge solutions to other fields using the topological groups symmetries that define their interactions.
NOTES
1One example of these moduli spaces is  The equivalences in this case are obtained by the classic Penrose transform
The equivalences in this case are obtained by the classic Penrose transform

where  is a homogeneous holomorphic line bundle on
is a homogeneous holomorphic line bundle on . In this case the complex
. In this case the complex  is a Dolbeault complex that is an elliptic complex on
is a Dolbeault complex that is an elliptic complex on  [30].
[30].
2Cousin Dolbeault theory refers to the complex Dolbeault infinite dimension.
3Our demonstration will consist of the fact that each of these subspaces of the complexes Cousin must be Hecke eigensheaves [14]. The sum of Hecke eigen-sheaves is the Hecke category in our result, which is twisted, since there are images of isomorphisms of Harish-Chandra modules (that is to say, in a category of Harish-Chandra whose D-modules are DF-modules) created via the Penrose transform on twisted modules. Here the property of being twisted is demonstrated by the argument of the Penrose transform that involve to the twistor transform in field theory.
Then the twistor transform followed from the Penrose transform 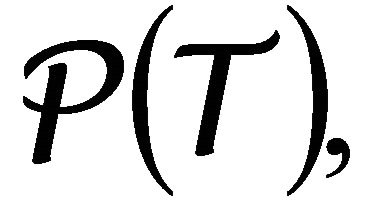 will calculate the kernels of the cohomological groups that are isomorphisms in the sense of the equivalence of the Kashiwara theorem. Nevertheless, we need a version of eigensheaves that include connections with regular singularities that could be extended through a pull-back of certain bundle of lines on BunG [6,23], to the irregular connections that there need no to be Verma modules, as it is mentioned in the Recillas conjecture [1]. In fact, the implications to that the above mentioned conjecture is valid, is the fact of considering regular connections to be the established for the Deligne theorem mentioned in the previous section, which is not clear when is want to extend them in the diverse ramifications of Langlands geometrical program [27,31].
will calculate the kernels of the cohomological groups that are isomorphisms in the sense of the equivalence of the Kashiwara theorem. Nevertheless, we need a version of eigensheaves that include connections with regular singularities that could be extended through a pull-back of certain bundle of lines on BunG [6,23], to the irregular connections that there need no to be Verma modules, as it is mentioned in the Recillas conjecture [1]. In fact, the implications to that the above mentioned conjecture is valid, is the fact of considering regular connections to be the established for the Deligne theorem mentioned in the previous section, which is not clear when is want to extend them in the diverse ramifications of Langlands geometrical program [27,31].
4This last, can be interpreted through the field theory like the flatness that characterize the background radiation in the spacetime producing the energy support of all variations of strings and heterotic strings that happen inside the deep space-time. To obtain interpretations in the frame of the topological gauge theories is necessary use the dual image of orbit space like orbifolds from the Calabi-Yau manifold that establishes relations between bundles of forms of fields on orbit  via a enclosed transform with Penrose transform. In this sense the
via a enclosed transform with Penrose transform. In this sense the  -resolution is given by the Penrose transform.
-resolution is given by the Penrose transform.