1. Introduction
The uncertainty relation, which displays an elementary property of quantum theory, was originally described by Heisenberg [1] as the relation between the error 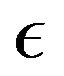 and disturbance
and disturbance 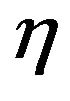 of a particle’s position and momentum as
of a particle’s position and momentum as
 (1)
(1)
where h is Planck’s constant.
Subsequently, a more generalized inequality was shown [2,3]:
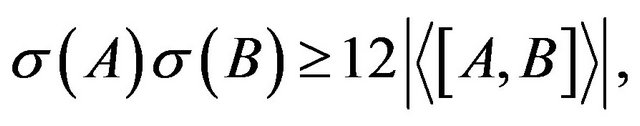 (2)
(2)
where  is the standard deviation of a self-conjugate operator X, which corresponds to some physical quantity, defined as
is the standard deviation of a self-conjugate operator X, which corresponds to some physical quantity, defined as
 , (3)
, (3)
with
 (4)
(4)
and  as the commutator of A and B.
as the commutator of A and B.
In some literature (for example, [4]), (2) is considered to be a more formal expression of (1).
Several decades later, Ozawa presented a more rigorous expression of the uncertainty relation [5-7]. The rootmean-square noise  and root-mean-square disturbance
and root-mean-square disturbance  are defined as
are defined as
 (5)
(5)
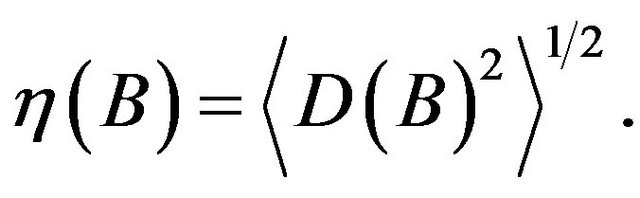 (6)
(6)
The Noise operator  is defined using the meter-observable
is defined using the meter-observable  of
of  as
as
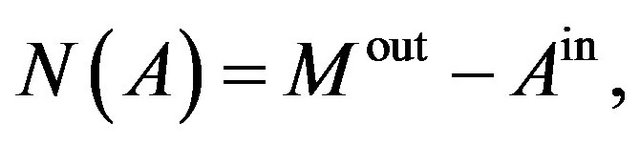 (7)
(7)
with the disturbance operator  as
as
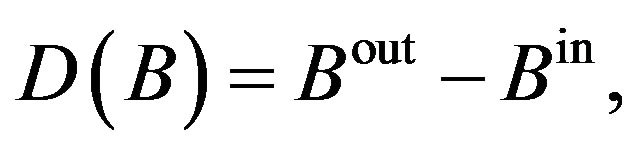 (8)
(8)
where in and out mean just before and just after measurement, respectively. The new uncertainty relation is written by means of (5), (6) and also (3) as
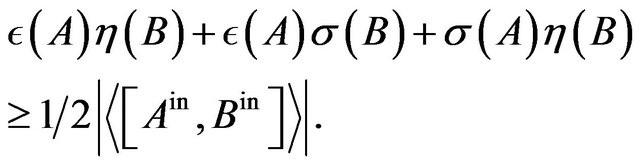 (9)
(9)
Recently, it was reported [8] that (9) was verified experimentally by a neutron spin experiment. Nevertheless, it is not clear whether verification of (9) is possible for continuous quantities such as position and momentum. In other words, it is not clear whether (5) and (6) are measurable for such quantities [9,10]. Watanabe et al. [11-13] suggested another inequality suitable for practical measurement.
Moreover, error and disturbance were defined in the identical state in Heisenberg’s thought experiment [1] referring to the uncertainty principle. If we follow his presupposition, the operators corresponding to error and disturbance should be simultaneously measurable. In many textbooks on quantum theory, commutativity of observables is regarded as a necessary and sufficient condition of possibility of simultaneous measurement. Ozawa, however, insists in his paper [14] that, in some states, two noncommutative observables, A and B, are simultaneously measurable if they satisfy
 (10)
(10)
and their meter observables are commutative. Simultaneous measurability has been discussed with respect to contextuality and weak measurement [14-17].
The purpose of this letter is to discuss the simultaneous measurability of error and disturbance. Firstly, we define simultaneous measurability from the quantum logical aspect. According to our definition, there exists no state where noncommutative observables are simultaneously measurable. Then, we define commutative operators which correspond to the error and disturbance of noncommutative observables. This definition leads to the uncertainty relation of error and disturbance in the identical state. A testable example of this relation is also suggested, where definition of error 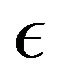 in [8] is shown to be insufficient for other settings.
in [8] is shown to be insufficient for other settings.
2. Simultaneous Measurability
To prepare for discussion about simultaneous measurability, we define observables according to a common quantum logical approach [18,19]. The proposition that a measured value of a physical quantity u belongs to a subspace A of space of real number R is written as . When the truth value of
. When the truth value of 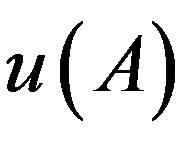 can be determined experimentally, u is called measurable. Logic L, which is nothing but a
can be determined experimentally, u is called measurable. Logic L, which is nothing but a  -complete orthomodular lattice, consists of such propositions. Classical logic is a Boolean lattice, namely, an orthocomplemented distributive lattice, while quantum logic is not.
-complete orthomodular lattice, consists of such propositions. Classical logic is a Boolean lattice, namely, an orthocomplemented distributive lattice, while quantum logic is not.
We suppose  -field
-field , which consists of all open sets belonging to space of real number R. A map u from
, which consists of all open sets belonging to space of real number R. A map u from 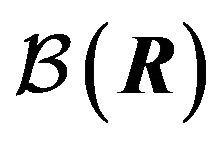 to logic L is called an observable of L if
to logic L is called an observable of L if
 (11)
(11)
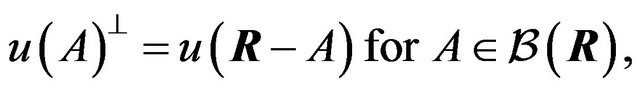 (12)
(12)
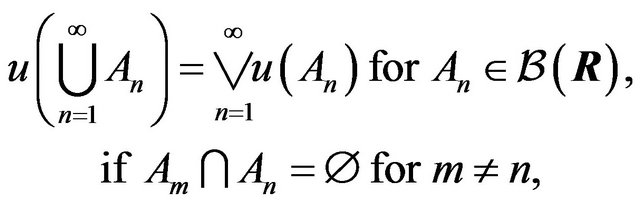 (13)
(13)
where 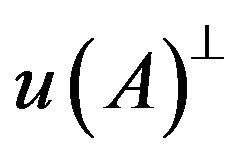 is the orthocomplement of
is the orthocomplement of  and
and 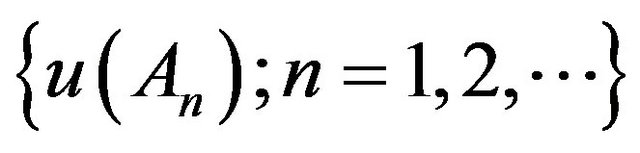 constitute an orthogonal set of projection operators. It is proved that observables are
constitute an orthogonal set of projection operators. It is proved that observables are  - homomorphism from
- homomorphism from  to L.
to L.
There exists a one-to-one correspondence between the whole set of bounded observables and the whole set of bounded self-conjugate linear operators. If, and only if, two such operators, which correspond to observables u and v, are commutative, they satisfy for any pair of 
 (14)
(14)
and the orthomodular lattice whose elements are ’s and
’s and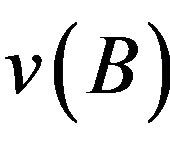 ’s is Boolean. Here, we assume, as usual, that all the measurable quantities are observables.
’s is Boolean. Here, we assume, as usual, that all the measurable quantities are observables.
We define the simultaneous measurability of observables u and v as follows.
Definition u and v are called simultaneously measurable if the truth value of 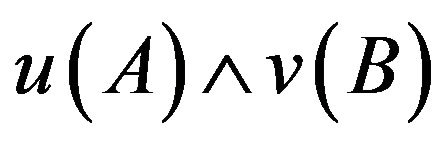 can be determined experimentally.
can be determined experimentally.
We present the following theorem:
Theorem Let u and v be observables of logic L and  ,
, 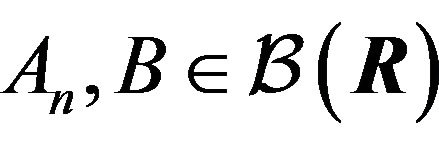 ,
,  for the fixed
for the fixed . Then,
. Then,  ,
,  are observables if, and only if, they satisfy (14).
are observables if, and only if, they satisfy (14).
Proof (sufficiency)
We assume (14) is satisfied. Firstly, we show the whole set  whose elements are
whose elements are ,
,  is a
is a  -complete orthocomplemented distributive lattice. Since
-complete orthocomplemented distributive lattice. Since ’s and
’s and  satisfy the distribution law,
satisfy the distribution law,

and 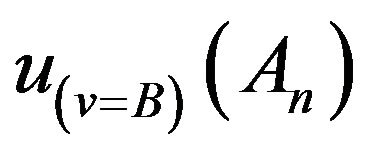 also satisfy the distribution law. Moreover, if we define
also satisfy the distribution law. Moreover, if we define
 (15)
(15)
for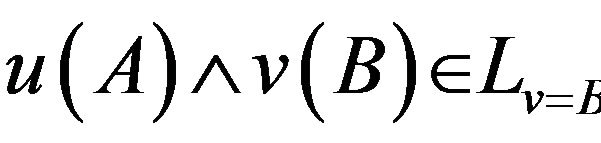 ,
, 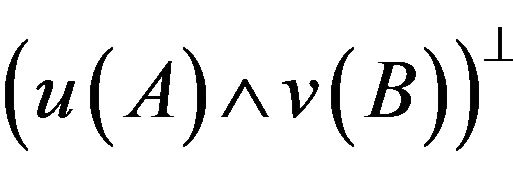 is the orthocomplement of
is the orthocomplement of . Thus
. Thus 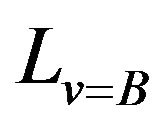 is a
is a  -complete orthocomplemented distributive lattice. It is clear that
-complete orthocomplemented distributive lattice. It is clear that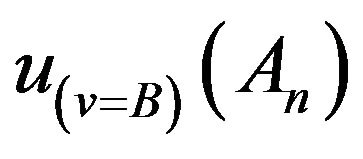 ,
,  satisfy (11)-(13) because
satisfy (11)-(13) because  is a distributive lattice. Therefore
is a distributive lattice. Therefore ,
, 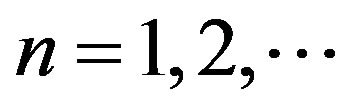 are observables of
are observables of  if they satisfy (14). (necessity).
if they satisfy (14). (necessity).
Let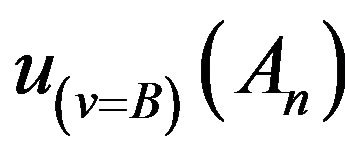 ,
, 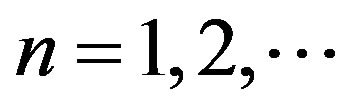 be observables. From (13)
be observables. From (13)

if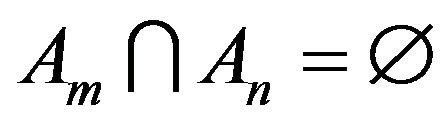 . This equation leads to
. This equation leads to

If we put ,
,
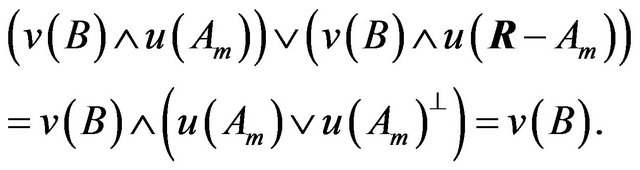
QED.
From the above, it is shown that  is not an observable if (14) is not satisfied, that is, two observables which correspond to mutually-noncommutative linear operators are not simultaneously measurable.
is not an observable if (14) is not satisfied, that is, two observables which correspond to mutually-noncommutative linear operators are not simultaneously measurable.
For example, let


be projection operators corresponding to 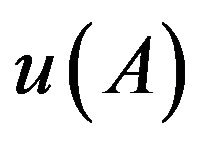 and
and , respectively, where
, respectively, where

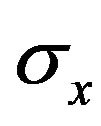 and
and 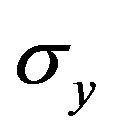 are Pauli spin matrices. Then, if
are Pauli spin matrices. Then, if , the projection operator corresponding to
, the projection operator corresponding to  is
is , which is not an observable.
, which is not an observable.
3. Uncertainty Relation
From the previous section, we can say such quantities as
 (16)
(16)
are not measurable because (7) and (8) are noncommutative when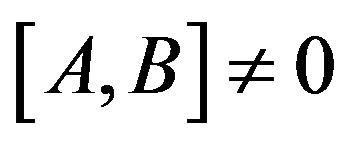 . Note that this fact does not deny (9) where (16) does not appear but (5), (6) and (3) do. These are measured separately by using states belonging to the same statistical ensemble. What we would like to emphasize is that the uncertainty relation should be written by means of commutative quantities if it is thought to be the relation between quantities which are measured in the identical state. Thus we define
. Note that this fact does not deny (9) where (16) does not appear but (5), (6) and (3) do. These are measured separately by using states belonging to the same statistical ensemble. What we would like to emphasize is that the uncertainty relation should be written by means of commutative quantities if it is thought to be the relation between quantities which are measured in the identical state. Thus we define
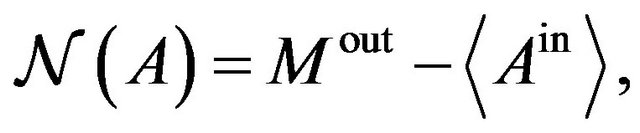 (17)
(17)
 (18)
(18)
as operators which express error and disturbance from the expectation values, respectively.
Using these operators, we examine the following quantity:
 (19)
(19)
Since  and
and  are observables in different systems, (19) becomes
are observables in different systems, (19) becomes

If we use
 (20)
(20)
 (21)
(21)
and assume
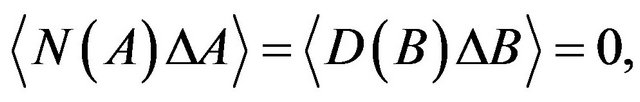 (22)
(22)
(19) is written by the use of (3), (5) and (6) as
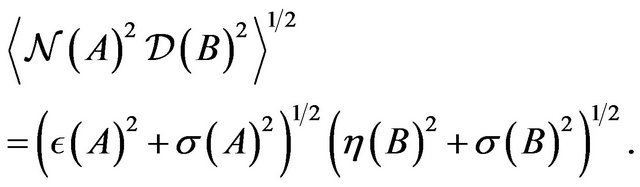 (23)
(23)
It is clear that (22) is not invariably realized. One of the simplest counter examples is the case where  always indicates
always indicates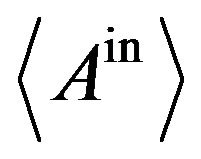 . Nevertheless, we regard (22) as a rather reasonable assumption, which means that
. Nevertheless, we regard (22) as a rather reasonable assumption, which means that  and
and 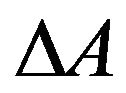 are independent stochastic variables, and so are
are independent stochastic variables, and so are  and
and .
.
We can calculate the lower bound of (23) by means of (2) and (9) to obtain
 (24)
(24)
If we use
 (25)
(25)
in place of (9), the minimal value becomes almost double:
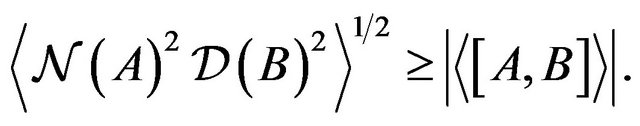 (26)
(26)
4. A Testable Example
In this section, we suggest an experiment with a setting which is a little modified from the experiment in [8] as a testable example of the inequality (24). We define A, B and OA instead of their definition in [8] as
 (27)
(27)
 (28)
(28)
where
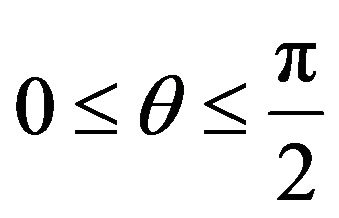
and . (22), which is necessary to conclude with (24), is satisfied in this setting. If the root-meansquare noise
. (22), which is necessary to conclude with (24), is satisfied in this setting. If the root-meansquare noise 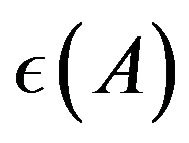 is completely calculable by using A, B and OA as insisted in [8],
is completely calculable by using A, B and OA as insisted in [8],
 (29)
(29)
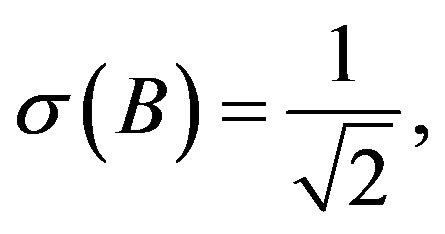 (30)
(30)
 (31)
(31)
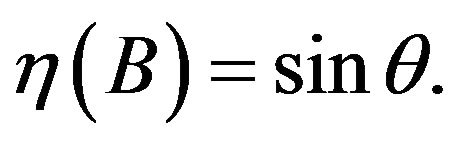 (32)
(32)
Then,
 (33)
(33)
and
 (34)
(34)
It comes down to that Ozawa’s inequality (9) is not realized within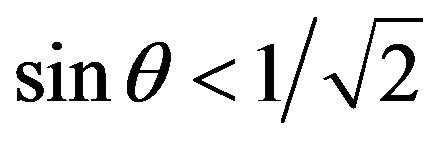 . This fact seems to show that
. This fact seems to show that 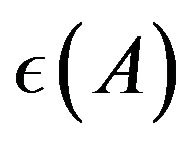 includes uncontrollable error.
includes uncontrollable error.
Accordingly, we will estimate the range of , including uncontrollable error, on the assumption that (25) or (9) is realized. We redefine
, including uncontrollable error, on the assumption that (25) or (9) is realized. We redefine 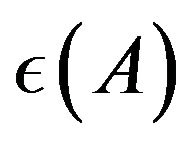 as
as
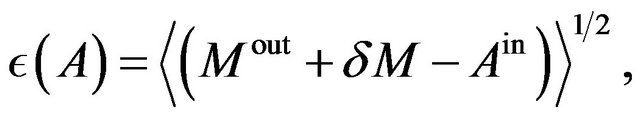 (35)
(35)
where  is the operator which gives uncontrollable error and is assumed to satisfy
is the operator which gives uncontrollable error and is assumed to satisfy
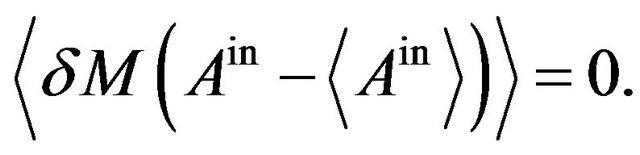
This assumption may demand that the angular momentum of the particle should be measured continuously. Then, inequalities corresponding to (26) and (24) will be derived from (23).
Firstly, if we assume (25),  independently of
independently of . Then,
. Then,
 (36)
(36)
The minimum value of the coefficient of the righthand side is 1 when .
.
Next, if (9) is assumed,
 (37)
(37)
Then
 (38)
(38)
The minimum value of the coefficient of the righthand side is  when
when .
.
If
 (39)
(39)
at some angles and
 (40)
(40)
at each angle are shown experimentally, we can conclude that Inequality (24) is realized. This is also an experimental proof that Ozawa’s inequality is correct.
5. Conclusion
To summarize, we have defined simultaneous measurability from the quantum logical aspect and conclude that operators corresponding to the error and disturbance should be commutative if they operate in the identical state. Moreover, a new inequality using such operators and a testable example are presented.