Method for Tentative Evaluation of Membrane Permeability Coefficients for Sodium and Potassium Ions in Unicellular Organisms ()
1. Theory of Method
The ion permeability of the plasma membrane has been recognized as an important problem in cell function. The main ions in cell physiology are protons, sodium, potassium and chloride ions, because of their participation in the building of transmembrane ions gradients, the support of cell potentials and energetics mechanisms in cells [1-4]. Permeability may be defined phenomenological as the amount of substance transported across a unit area in unit time as the result of a unit force [5,6]. Permeability of given solutes is characterized by the permeability coefficient, measured by the amount of solute passing in unit time through unit area of membrane under the influence of unit concentration gradient [7]. The dimension of permeability coefficient is in meter per second if membrane area is given in m2, cell volume in m3 and concentration of solutes is given in mol per liter [8].
A guiding principle in the estimation of the permeability coefficient is that the cell boundary acted as a lipidlike phase through which the penetrating solute diffused. A simple hypothesis based on Fick’s laws of diffusion is that the instantaneous rate of uptake of the solutes (ds/dt) through the semi-permeable bounding membrane, into a vesicle (liposome or cell) of volume (V), is represented as the product of the surface area (S) of vesicle, the difference in solute concentration between the interior (Cin) and exterior (Cex) compartments (Cex − Cin), and the permeability coefficient (P) that connect the diffusion coefficient of solutes, thickness of membrane and relative solubility of substances in water-oil phases [9].
The relevant equations are:
 (1)
(1)
and
 (2)
(2)
where Cex and Cin are function of the time.
When cell surface area S, cell volume V and exterior concentration Cex (because of big exterior volume) are constant, these two equations simplify to:
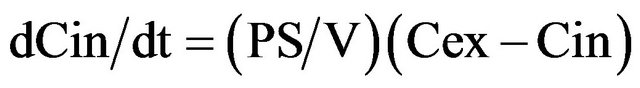 (3)
(3)
After integration we receive for concentration Cin(t) in vesicle after time t :
 (4)
(4)
where Cin(0) is the concentration of solute in vesicle at the moment t = 0.
The equation (PSt)/V = kt represents the connection between permeability coefficient P(m/s) and the firstorder rate constant k(t−1) :
 (5)
(5)
The initial concentration of solute in cell, at the moment t = 0 is assumed to be zero, and for C(0) = 0 the Equation (4) receives the form:
 (6)
(6)
For the natural logarithm of Equation (6) we’ll receive for permeability coefficient:
 (7)
(7)
The Equations (4) and (7) keep validity for measuring the permeability coefficient in vesicle and liposome (in vitro) and cell (in vivo).
For vesicles and liposome, the gradient of solute concentration ∆C = Cex − Cin dissipates up to equilibration of concentration in the interior and exterior compartments i.e. up to Cex = Cin. In this case the Equations (4) and (7) describe the establishment of the equilibrium concentration in the internal volume of the vesicle or liposome, following an exponential law equation. In this case the permeability coefficient is calculated from Equation (5) after experimental measuring of first-order rate constant “k” [10].
By empiric way, we established that the Equation (7) may be applied for calculation of permeability coefficient of ions passing trough outer cell membrane in growing cells. In all growing cells the transmembrane concentration of sodium and potassium ions maintained on constant level by the active transport of cell. For these ions the ratio Cin(t)/Cex is a constant and don’t depend on the time. For time-period equal to generation (doubling) time (Tgt) the mother cell grows and divided by binary. Similarly to the mother cell, a daughter cell has same cellular characteristics, including transmembrane distribution of sodium (Na+) and potassium (K+) ions. For time t = Tgt the Equation (7) received the form:
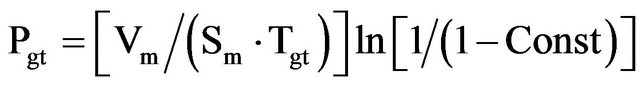 (8)
(8)
where Pgt presents the membrane permeability of cells. The volume Vm, surface Sm and genera tion time Tgt presented the maximum values of volume, surface and generation (doubling) time of cell. The Cin(Tgt)/Cex ratio is given to be the constant (Const).
Because of every unicellular organism grows up to nearly the same maximum volume and surface, in the moment of end of cell cycle the Vm/Sm ratio of daughter cell is equal to the volume to surface ratio of mother cell. Thus, for given unicellular organism the volume to surface ratio has nearly a constant value in the end of cell cycle, independently of duration of generation time. For small Prokaryotes to big Eukaryotes (from bacteria to amoebas) the volume to surface ratio changes about 4 orders of magnitude [11-14]. The generation time from bacteria to amoeba changes about 4 orders of magnitude too ([11,15-19]. In unicellular organisms the transmembrane concentration of Na+ and K+ ions (ion gradient Cin/Cex) change maximum 103 - 104 folds [1,2,20]. Because of that, the term ln[Cin(Tgt)/Cex] and consequently ln[1/(1 − Cin(Tgt)/Cex)] changes maximum 3 - 4 fold. Thus, the permeability coefficient Pgt in Equation (8) depends firstly, on volume to surface ratio and generation time (changing 104 folds), and secondly from ln[1/(1 − Cin(Tgt)/Cex)] (changing 3 - 4 fold).
This gives us the reason to simplify the Equation (8) as:
 (9)
(9)
where Pgt shows the value of permeability coefficient in end of cell cycle, in the moment t = Tgt.
On Figure 1 schematically are presented tree fashions of growth and dividing of unicellular organisms by binary, from which is observed that the volume to surface ratio in mother and daughter cell remains relatively constant.
Accordingly Formula (9), the permeability coefficient (Pgt) characterizes permeability of ions, passing trough the area of outer cell membrane (Sm), which limits the total cell volume (Vm) for time-period, equal to the duration of the cell cycle (Tgt). The ions acting in the area of outer cell membrane could be sodium, potassium and chloride ions. In outer cell membrane are localizes the Na+ − K+ ion pumps of active transport, which creates and maintain the constant transmembrane gradients of these ions [21].
The permeability coefficient of K+ and Na+ ions (including CI− ions), falls in diapason of 1.0 × 10−14 - 1.0 × 10−10 m/s [6,7,22]. Scaling of permeability coefficients of
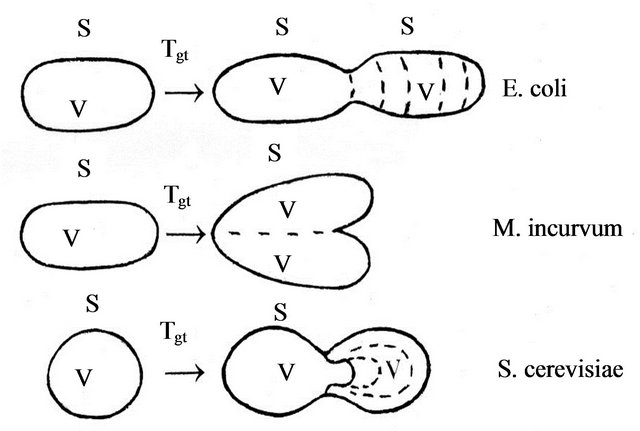
Figure 1. Growth and dividing by binary of Prokaryotes and Eukaryotes (E. coli, S. cereviseae and M. Incurvum), accordingly to Holt [15-18] and Hausmann [12] (Legend: by V, S and Tgt are signed cell volume, surface and generation time).
solutes passing trough outer cell membrane has showed that the sodium, potassium and chloride ions have the lowest permeability in comparison to other solutes (divalent ions, protons, phosphate, glucose, water and metabolites) [22]. The permeability coefficient of Na+, K+ and CI− ions don’t differ more than one order of magnitude [7,14]. The permeability coefficient of sodium ions is lower than coefficient for potassium and chloride ions, whereas the permeability coefficient of potassium and chloride ions is lower than those of protons [3,23,24].
Because of the protons act in the mitochondrial membrane (inside in the cell volume) and life cycle of mitochondria differ from life cycle of cells, the relatively high permeability coefficient for protons range in diapason of 1.0 × 10−10 − 1.0 × 10−8 m/s and can be connected rather with mitochondrial processes than the processes in outer cell membrane.
2. Data and Methods
The data for body mass (M, kg), temperature of growth (t, ˚C), minimum, maximum and mean generation (doubling) time Tgt (min, h, d) of cells and calculated data for volume to surface ratio (V/S, m) for 14 unicellular organisms (Prokaryotes and Eukaryotes) are presented on
Table 1.
The data for temperature of growth and generation time are given from the same sources. The mean generation time of cells is calculated as:
 (10)
(10)
Calculation of the volume to surface ratio in unicellular organisms was made accordingly source [25] by formula:
 (11)
(11)
The value for body density (r) of unicellular organisms is given to be 1100 kg/m3 and coefficient (k) is given to be 0.0542, accordingly data by Schmidt-Nielsen [26].
Calculation of the membrane permeability coefficient Pgt(m/s) equal to volume/(surface × generation time) ratio was made, accordingly theory of method by formula:
 (12)
(12)
In Formula (12) the body mass (M) is in “kg”, the volume to surface ratio (Vm/Sm) is in “m” and generation (doubling) time (Tgt) is in “s”. The mean membrane permeability can be calculated as:
Table 1. Body mass, calculated accordingly Formula (11) volume to surface ratio and generation time in some Prokaryotes and Eukaryotes.

 (13)
(13)
or
 (14)
(14)
For calculation of Pmax and Pmin, the minimum (Tmin) and maximum (T max) generation times are used.
The experimental data for sodium and potassium permeability coefficients (PNa+ and PK+) are received by three fashions. Firstly, from published in scientific literature data for sodium and potassium permeability coefficient. Secondly, by calculation of membrane permeability coefficient, accordingly Fick’s law dividing mass flux of ions Ji (mol/m2·s) passing trough external cell membrane to ion concentration Cin (mol/m3) in cells [5]:
 (15)
(15)
The data for mass flux and internal concentration of sodium and potassium ions were given from published in scientific literature data.
Thirty, by calculation of sodium and potassium permeability coefficients as a product between first-order rate constant k (in s−1) and volume to surface ratio of cell V/S (in meter), accordingly Stein [8], and Yamauchi et al. [10]:
 (16)
(16)
The data for first-order rate coefficient were given from scientific literature sours.
Statistical software “STATISTICA” was used for calculation of means ± standard deviation (SD), and correlation coefficients.
3. Results
In given on Table 1 data for 14 unicellular organisms, the mass of unicellular organisms changes 12 orders of magnitude, from 3.0 × 10−16 kg in Psychrobacter immobilis to 1.32 × 10−4 kg in Hydrodyction africanum. The volume to surface ratio changes 4 orders of magnitude, from Psychrobacter immobilis (1.26 × 10−7 m) to Hydrodyction africanum (5.24 × 10−3 m). The generation time changes nearly 4 orders of magnitude too, from 20 min in Escherichia coli to 150 days in Hydrodyction africanum.
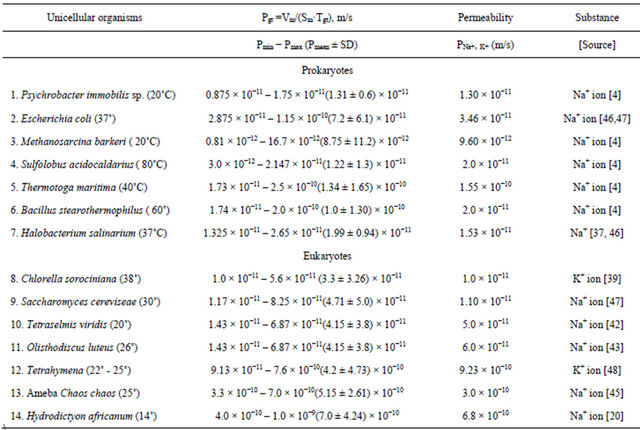
In Table 2 are given the calculated data for minimum (Pmin), maximum (Pmax) and mean (Pmean ± SD) permeability coefficients accordingly formulas (12 - 14), and experimental measured data for sodium and potassium membrane permeability coefficient (PNa+, K+) in 7 Prokaryotes and 7 Eukaryotes.
Table 2. Calculated data for minimum (Pmin), maximum (Pmax), mean permeability coefficient (Pmean ± SD) and experimental data for permeability coefficient of sodium (PNa+), and potassium (PK+) ions.
\
In given on Table 2 data set, the calculated diapason of values for mean permeability coefficient in Prokaryotes change about 2 orders of magnitude (from 8.75 × 10−12 m/s in Methanosarcina barkeri to 1.34 × 10−10 m/s in Thermotoga maritima) and overlaps with diapason of experimental data for permeability coefficients for sodium (PNa+) and potassium (PK+) ion (from 9.6 × 10−12 m/s in Methanosarcina barkeri to 1.55 × 10−10 m/s in Halobacterium salinarium).
In given on Table 2 data set the calculated diapason of values for mean permeability coefficient in Eukaryotes change about 1 orders of magnitude (from 3.3 × 10−11m/s in Chlorella sorociniana to 5.78 × 10−10 m/s in Hydrodictyon africanum) and overlaps with diapason of experimental data for permeability coefficient for sodium and potassium ions (from 1.0 × 10−11 m/s in Chlorella to 9.23 × 10−10 m/s in Tetrahymena). The summarizing diapasons of data for mean permeability coefficients in Prokaryotes and Eukaryotes, accordingly Table 2 are given on Figure 2.
On Table 2, the calculated data for Pmean coefficient and the experimental data for PNa+, K+ coefficient differs less than one order of magnitude. From 14 studied organisms, in 12 organisms (P. immobilis, E. coli, M. barkeri, S. acidocaldarius, T. maritime, H. salinarium, Ch. Sorociniana, T. viridis, O. luteus, Tetrahymena, Ch. chaos, H. africanum) the ratio between calculated and experimental values of permeability coefficients (Pmean/PNa+, K+) changes from 1 to 3 folds. In two organisms only (Bacillus stearothermophilus and Saccharomyces cereviseae) this ratio is 4 - 5 folds.
On Figure 3 is given in more details the comparison between the mean calculated values (Pgt = Pmean) and experimental values of coefficient (PNa+, K+), where two values are situated on the horizontal and vertical axis on coordinate system in the same scale. The position of the points with coordinates (Pgt, PNa+,K+) is compared with the position of the points with equal coordinates on equilibration line of Pgt = PNa+, K+. The position of intersection coordinate (Pgt, PNa+, K+) on Figure 3 don’t lies more than one order of magnitude from the equilibration line of Pgt = PNa+, K+. This shows that the relation from type PNa+, K+ ≈ Vm/(Sm·Tmean) is valid within an order of magnitude. The correlation coefficient between Pgt and PNa+, K+ values is 0.845 which shows that this relation is not random.
For minimum Tmin and maximum Tmax generation time, the corresponding calculated permeability coefficients are Pmax = Vm/(Sm·Tmin), and respectively Pmin = Vm/ (Sm·Tmax). Because of the validity of the ratio Tmin < Tmean < Tmax, and corresponding ratio Pmin < Pmean < Pmax, the interval of values between Pmin and Pmax contained membrane permeability coefficients for sodium and potassium ions i.e. the relation Pmin < PNa+, K+ < Pmax is valid.
In summary, the proposed method can solve two main tasks. In the first task, knowledge of the minimum and maximum generation time of cells dives possibility to determinate the interval, which contained permeability coefficients for sodium and potassium ions. In the second task, knowledge of the mean generation time of the cells gives possibility to determinate, with accuracy of an order of magnitude, permeability coefficient for sodium and potassium ions. The accuracy of the method is determined by the two terms of Equation (8):
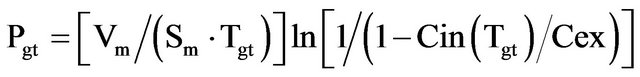
Ignoring the term ln[1/(1 − Cin(Tgt)/Cex)] brings error 3 - 4 times, and giving in the mind that the term (Pmean/ PNa+, K+) brings error 3 - 4 times, the product between two errors gives 9 - 12 times summarized error. For two organisms only (Bacillus stearothermophilus and Saccharomyces cereviseae), where (Pmean/PNa+, K+) ratio is 4 - 5 times, the summarized error is 12 - 15 times. This shows that the maximum error of the methods is about one order of magnitude. For better evaluation of permeability coefficient is needed to calculate the term ln[1/(1 − Cin(Tgt)/Cex)] in Equation (8), which will reduce the error 3 - 4 times and make at least one order of magnitude. The proposed method can be improved for specific groups of microorganisms with similar characteristics.
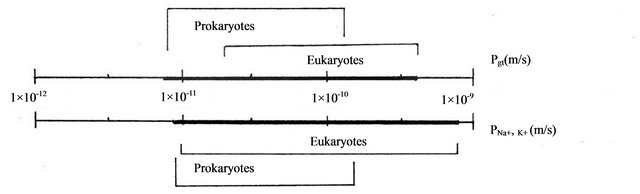
Figure 2. Scaling diapasons of calculated (Pmean) and experimental (PNa+, K+) values of permeability coefficient for sodium and potassium ions. The full diapasons of calculated and experimental values of coefficients in Prokaryotes and Eukaryotes overlap and is marked by solid line on the figure axes.
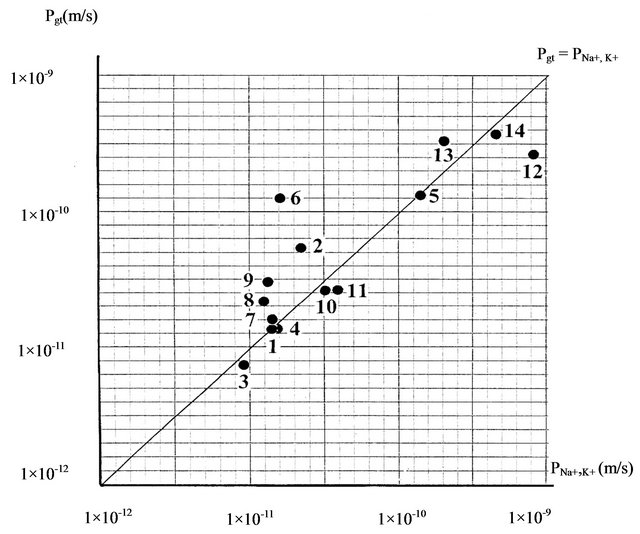
Figure 3. Scaling of mean permeability coefficient Pgt, and experimentally measured membrane permeability coefficients PNa+, K+ for sodium and potassium ions in 14 unicellular organisms: 1—P. immobilis, 2—E. coli, 3—M. barkeri, 4—S. acidocaldarius, 5—T. maritime, 6—B. stearothermophilus, 7—H. salinarium, 8—Ch. Sorociniana, 9—S. cereviseae, 10—T. viridis, 11—O. luteus, 12—Tetrahymena, 13—Ch. chaos, 14—H. africanum.
4. Discussion
A new method requires measure the mass or volume, surface and minimum and maximum generation time of the unicellular organism at given growing conditions. At different growth conditions (temperature of growth, substrates, air pressure and others) the generation time can change inordinately, while cell mass, volume and surface of organisms keep on relatively constant level, because the cells grow always up to gain the maximum values, before cell division. Minimum and maximum generation time can be measured by the change of the experimental conditions or can be taken from microbiology scientific sources. Recently, in this direction are accumulated many data for every cell line.
In some previous works Atanasov [14] lanced the hypothesis that the volume/(surface·lifespan) ratio in cells correlated to minimum membrane permeability of cells, namely the membrane permeability to sodium and potassium ions [19]. The mechanism of cell control on potassium and sodium ion permeability is not clear, in contrast to the mechanism of ion permeability of protons [25, 49,50]. From the given experimental data is shown that there is a relationship between the volume, surface, generation time and the membrane permeability to sodium and potassium ions in unicellular organisms. As the author has shown, a similar relationship exists between the volume, surface and lifespan of multicellular organisms (animals) [22]. Because this relationship seem to be universal, it is possible to express one cell mechanism to control and maintain minimum membrane permeability in cell membrane, and in particular the permeability of sodium and potassium ions.
However, the mechanism of maintenance of lowest permeability of sodium and potassium ions in cells is not clear. The independence of their permeability coefficient to membrane composition [4] leads to model, in which the permeability coefficient depends mainly on spatialtime parameter of cells. From an evolutionary point of view, this dependence is associated with the emergence of life in the aqueous environment of the oceans the main ion composition is represented mainly by sodium, potassium, chloride ions, protons and hydroxyl ions.
5. Conclusion
The established theoretic equation between membrane permeability, volume, surface and generation time in unicellular organisms allows to calculate sodium and potassium ion permeability in these organisms. It is possible the equation to express cell mechanism for control the permeability of sodium and potassium ions.