The Context of Knowledge and Data Discovery in Highly Dense Data Points Using Heuristic Approach ()
1. Introduction
Clustering is an accepted unsupervised knowledge approach functioned in areas, such as image processing, data mining, bioinformatics and pattern recognition. Clustering classifies the data significantly by combining analogous data points in a group and dividing divergent data points in diverse clusters. Usually, the comparison among data points is charged with the assist of a difference or distance appraise, for instance Euclidian distance. Classical clustering technique by k-means splits the data into k panels so that the amount of square-error among cluster means and the data in the equivalent cluster is decreased. The k-means process falls beneath the group of dividing methods for clustering.
Hierarchical methods of clustering generate a hierarchy of clusters. In an agglomerative chain of command, lesser clusters are combined to build superior clusters, initiating from separate data points primary to a distinct cluster. Under a discordant hierarchy, bigger clusters are spitted to structure smaller clusters. The divisive approach initiates with a distinct cluster, and at last, every data point communicates to a cluster. The preferred clustering can be produced by wounding the hierarchy at a prearranged depth. Density-based clustering techniques develop clusters supported on solidity of data points in the clustering gap. Not like dividing techniques, the density-based techniques are able to notice clusters of subjective shapes. In the model-based clustering technique, each cluster is symbolized by a parametric representation. A data point is dispensed to the group whose model elucidates the data points finest. A representation, such as Gaussian mixture model (GMM) or hidden Markov model (HMM) is definite a priori supported on the field information.
Clustering problems concerning image data, for instance image segmentation, action segmentation, stereo system inequality segmentation, and structure-and-motion segmentation, can be articulated as model-based clustering troubles. For model-based clustering troubles, to allocate a data point data to a suitable group, the cluster parameters are supposed to be recognized. Alternatively, the cluster parameters can be calculated only if the cluster course works are recognized. This “chicken-andegg” quandary directs to an iterative expression for model-based clustering techniques analogous to anticipation maximization (EM) algorithm.
Clustering intends to optimize an obligation cost to attain a (nearby) most favorable solution. If the number of clusters is enlarged, normally the cost for the similar data decreases. The disintegration folder for this occurs when one group communicates to one data point and the equivalent clustering cost is zero. Obviously, such a situation is adverse. Thus the clustering charge must be castigated for further clusters. A selection of model-selection techniques subsist, which integrate this idea. Make a memo of that the name “model” in representation refers to the collection of the amount of clusters and the parametric representation for these clusters. To pertain model collection to clustering, applicant models are produced successively by changing the number of clusters, and the finest model consistent with a model-selection principle is chosen. For the image data, the iterative and chronological crisis of model collection can be reduced to a one-step optimization by employing the information that the clusters produced in an image are spatially rational.
In this work, we are going to analyze the model selection clustering is first initiated through the process of heuristic training sequences on image data points and appropriates the problem—specific characteristics.
2. Literature Review
Clustering is an accepted unsupervised knowledge approach functioned in areas, such as image processing, data mining, bioinformatics and pattern recognition. An imperative crisis connected with clustering (esp. in the situation of density evaluation) is the fortitude of the number of amendable model constraints. Model collection approaches in clustering contain mainly on the trouble of shaping the number of workings/clusters. Branchand-bound methods [1] are employed in different data study problems, for instance clustering, serration and feature collection. Traditional techniques of branch-andbound based clustering investigate during mixtures of different partitioning potentials to optimize a clustering cost. Nevertheless, these techniques are not virtually practical for grouping of image data where the size of data is huge.
The conventional searching technique for model-order collection in linear deterioration is a nested full-parameters-set penetrating process over the preferred orders, which describe full-model order collection. In [2], proposed the model-selection searching technique for form order collection, which recognize restricted model order collection. A model selection algorithm [3] for a nonlinear structure recognition technique is proposed to revise practical magnetic quality imaging (fMRI) efficient connectivity. The crisis of model selection happens in a number of contexts, for instance compressed logic, division collection in linear deterioration, inference of structures in graphical models, and signal denoising. In scrupulous, it used two procedures of coherence [4] to present an in-depth examination of an easy one-step threshold (OST) algorithm for model collection. An iterated algorithm for model collection is proposed in [5], which can routinely present the best form of clusters and expected [6].
Clustering has been a focus of widespread research in data mining, model detection and other areas for numerous decades. The major objective is to disperse samples, which are naturally non-Gaussian and uttered as points in high-dimensional characteristic spaces, to single of a number of clusters. In [7], offer a distinction supposition structure for unsupervised non-Gaussian model collection. For the learning of the model, the author in [8] believes both Bayesian and information-theoretic techniques during stochastic density. On the source of the cluster strength, the paper [9] proposed a collection model to recognize the number of clusters. Numerous improvements and heuristics [10] for humanizing model selection, counting the alteration of well-known techniques. A significant component of the unsupervised learning crisis [12] is shaping the number of clusters [11] which finest explain the data. In this work, we are going to analyze the model selection clustering is first initiated through the process of heuristic training sequences on image data points and appropriates the problem-specific characteristics.
3. Proposed Model-Selection Clustering for Image Data Point Using Heuristic Approach
The proposed work is efficiently designed for identifying the best model selection for the analysis of image data points through heuristic approach. Model selection is a division of statistics and information theory, which is apprehensive with recognizing the precise parametric representation for a specified set of data. This is proficient by suiting diverse models to the given data point of the image, and devising a trial and error method, which consigns a scalar to each of the models. The form with the finest score is then chosen as the most suitable one. The essential input for the model selection practice is a surplus position of M supposed object actions, each specified by a set of image point paths practical during some part of the sequence. The architecture diagram of the proposed model selection clustering for image data point using heuristic approach (MSCHA) is shown in Figure 1.
3.1. Model Selection
The crisis of the model selection is formulated here based on the different problem characteristics. Consider a set of M observations O, such as image intensity/color, video motion or stereo disparity [1],
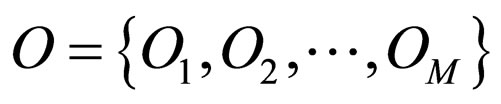 (1)
(1)
The corresponding cluster memberships for the observations can be denoted by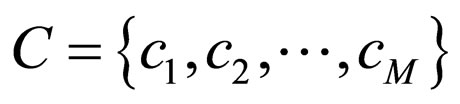 . If an observation Oj belongs to a cluster k then Cj = k and vice versa. Under the model-based clustering paradigm, the data can be explained with one of the K clusters with parameters
. If an observation Oj belongs to a cluster k then Cj = k and vice versa. Under the model-based clustering paradigm, the data can be explained with one of the K clusters with parameters , respectively. A general representation for guessing observations from the cluster constraints and the memberships could be specified as
, respectively. A general representation for guessing observations from the cluster constraints and the memberships could be specified as
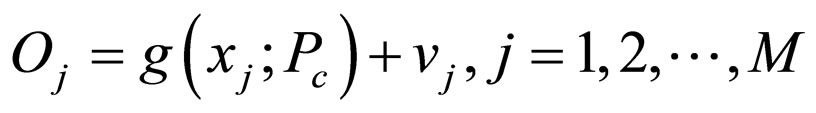 (2)
(2)
In model,  are the independent variables on which the observations O depend (these can be quantities, such as spatial locations for images or time instances for time-series data). If the data do not have spatial or temporal relationship, which is true for many clustering problems, the independent variables would not appear in the model. g (x'PC) can be a linear or nonlinear function or any process that can compute observation o from x given parameters Pf.
are the independent variables on which the observations O depend (these can be quantities, such as spatial locations for images or time instances for time-series data). If the data do not have spatial or temporal relationship, which is true for many clustering problems, the independent variables would not appear in the model. g (x'PC) can be a linear or nonlinear function or any process that can compute observation o from x given parameters Pf.  the noise demeaning the surveillance, which is normally implicit to go behind a zero mean autonomous Gaussian distribution. The above model appears in the missing data problems as well. According to the missing data formulation, the observations O are available and the cluster memberships C are missing.
the noise demeaning the surveillance, which is normally implicit to go behind a zero mean autonomous Gaussian distribution. The above model appears in the missing data problems as well. According to the missing data formulation, the observations O are available and the cluster memberships C are missing.
The model-based clustering problems have two unknown quantities, the cluster parameters
 and the memberships C. Given the memberships C, the maximum likelihood estimate for the parameters P is given by
and the memberships C. Given the memberships C, the maximum likelihood estimate for the parameters P is given by
 (3)
(3)
Conventional methods for model-based clustering iterate between estimation of the model and L till one or the other converges. They additionally require that the number of clusters K is known a priori. This requirement is unrealistic for most clustering problems. Thus the number of clusters has to be varied to select the optimal number of clusters. This process is called model-selection. The model-selection constitutes to the choice of K and corresponding P. Since the likelihood of the model increases as more clusters are added, a criterion which penalizes the likelihood with increasing clusters, such as Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) is used to select the optimal number of clusters.
Imagine a collection of N data objects X (e.g., sequences), symbolized by  and xN, and K probabilistic generative representations (e.g., HMMs),
and xN, and K probabilistic generative representations (e.g., HMMs),  , each consequent to a group of data objects. The diagram shown (Figure 2) below describes the connections among the data and models. The models generally enclose members of probabilistic models. A model ly can be analyzed as the widespread “centroid” of cluster y, while it classically presents a much comfortable depiction of the cluster than a centroid in the data point. A association among an object x and a model ly specifies that the object x is being connected with cluster y, with the association weight (closeness) among them given by the log-likelihood log p (xjly).
, each consequent to a group of data objects. The diagram shown (Figure 2) below describes the connections among the data and models. The models generally enclose members of probabilistic models. A model ly can be analyzed as the widespread “centroid” of cluster y, while it classically presents a much comfortable depiction of the cluster than a centroid in the data point. A association among an object x and a model ly specifies that the object x is being connected with cluster y, with the association weight (closeness) among them given by the log-likelihood log p (xjly).
The design of presenting clusters by models simplifies the model selection algorithm, where both data objects with models and cluster centroids are in the similar data space. The models also present a probabilistic analysis of clusters, which is an enviable characteristic in several applications. The model based clustering is simply defined under the control of probabilistic generative representations with consequent set of objects.

Figure 1. Architecture diagram of the proposed MSCHA.
3.2. Heuristic Technique for Model Selection
Heuristic technique specifies to knowledge based approach for crisis solving, learning, and detection. Where a comprehensive exploration is impossible, heuristic methods are utilized to accelerate the course of deciding a satisfactory solution. Examples of heuristic approach comprise by a rule of thumb, an instinctive decision, or common sense. The most essential heuristic form is trial and error, which is to be to identify the standards of variables in algebra problems. A heuristic technique considered for resolving a problem when standard methods are too time-consuming for judging an estimated elucidation. By dealing optimality, comprehensiveness, exactness, and/or accuracy for rapidity, a heuristic might rapidly create a explanation that is sufficient for solving the problem.
A heuristic valuation is a usability testing method developed by skilled usability guides. In software improvement, the exercise of a heuristic technique can assist a well-designed user line, allowing users to find the way of complex systems instinctively and without obscurity. The interface might direct the user when essential (Figure 3).
Trial and error, is a tentative technique of problem resolving also termed as generate and test. This technique could be processed under two basic techniques to problem solving and is compared with an approach utilizing imminent theory.
Trial and error has a number of features:
• Solution-oriented: trial and error constructs no effort to determine why a solution works; simply that it is a solution.
• Problem-specific: trial and error builds no effort to simplify a clarification to other troubles.
• Non-optimal: trial and error is usually an effort to discover a resolution, not all results, and not the best elucidation.
• Needs diminutive information: trials and error can progress where there is slight knowledge of the subject.
For a given data point in a image, there might be different models based on different characteristics that need to be applied. Based on the characteristics of the problem, the user has to choose the model for a particular type of the process. In the proposed MSCHA, the process of selecting the model is based on the process of heuristics training sequences. The heuristic process followed trial and error process which formed a set of assumptions and matched with the solution of the given problem. If it matched exactly, the technique stops its process. The process of models selection criterion using heuristic technique is shown in Figure 4.
Here in this work, we proposed heuristic technique for identifying the best model based on problem characteristics. Normally, for a data point in a given image, consists of different model. To choose the model based on problem characteristics, heuristic approach is used. It keeps on trying the process of identifying the solution until the best solution reaches and matches with the characteristics of problem. It is probable to utilize trial and error to discover all solutions or the finest solution, when a test ably restricted number of probable solutions subsist. To discover all solutions, one merely creates a message and persists, fairly than finishing the process, when a clarification is established, until all solutions have been attempted. To discover the best solution, one discovers all solutions by the technique just explained and then moderately estimates them supported upon some predefined deposit of measure, the subsistence of which is a form for the prospect of ruling a best solution. The next section describes about the experimental evaluation of the proposed model selection clustering for image data point using heuristic approach.
4. Experimental Evaluation
The proposed heuristic approach is efficiently used for model selection clustering through image data point. The proposed model selection clustering for image data point using heuristic approach is implemented in Java. An experimental evaluation is conducted on the proposed model selection clustering for image data point using heuristic approach (MSCHA) with real and synthetic data sets extracted from research repositories (UCI). At first, group parts of image which has analogous motion. To

Figure 3. Process of model selection criterion using heuristic technique.
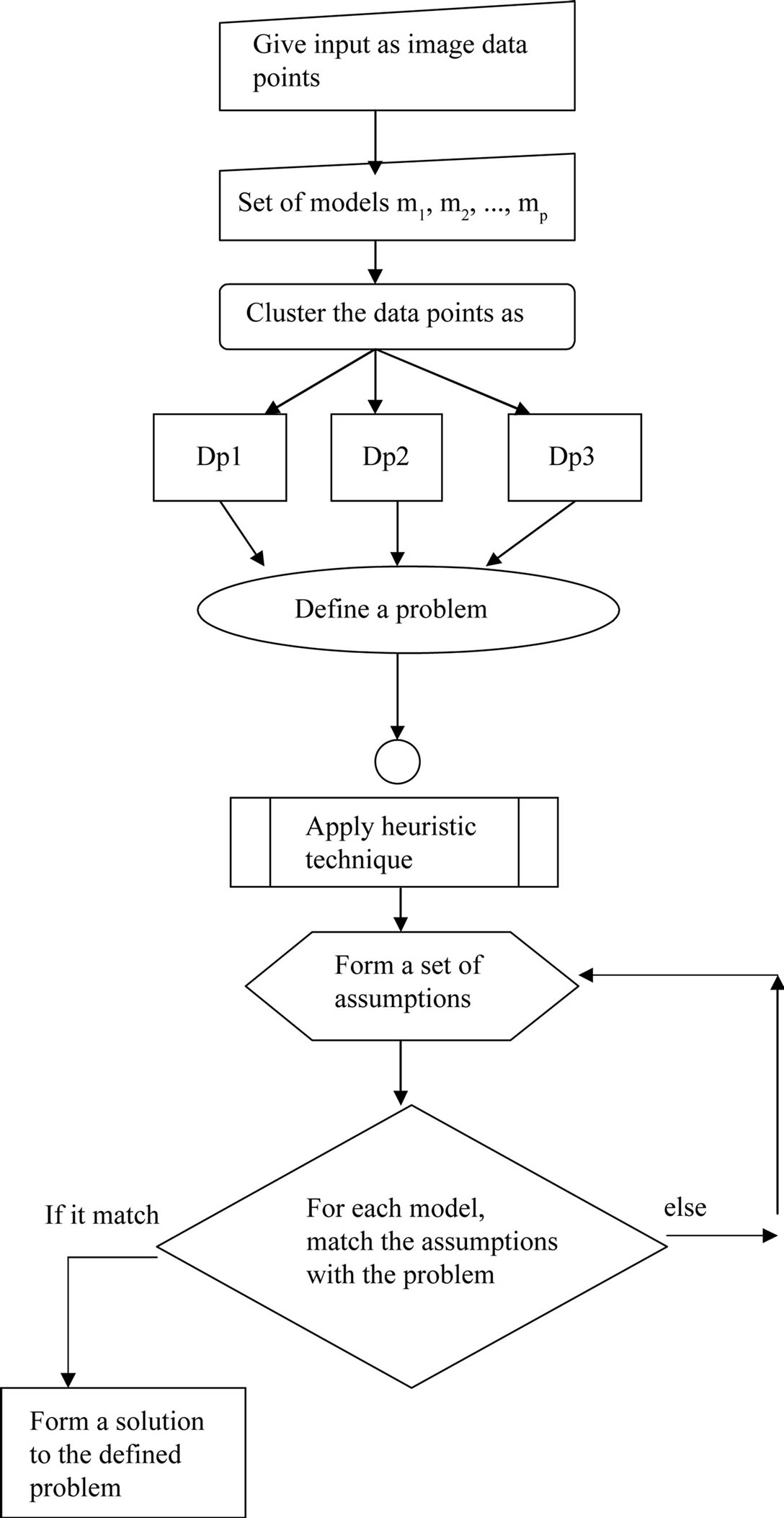
Figure 4. Flowchart for model selection criterion algorithm.
generate candidates for the proposed model-selection approach through the process of heuristic, for each image correspondence, perform trial and error method to identify the best solution. The heuristic approach will keep on forming the set of training sequences until it found a model to be matched with the problem characteristics of the data point. The process was taken place until the best solution is identified for the specified problem characteristics. The performance of the proposed model selection clustering for image data point using heuristic approach is measured in terms of:
1) Computational complexity2) Detection rate of the best model3) Time consumption.
5. Experimental Evaluation
In this work, we have seen how the best solution has been identified through the process of heuristic training sequences on image data points and appropriate the problem-specific characteristics. The outcome of the proposed model selection clustering for image data point using heuristic approach is compared with an existing Branch-and-Bound for Model Selection and Its Computational Complexity (BMSCC).
The above Table 1 describes the computational complexity of the models formed based on the data points presents in the image. The computational complexity of the proposed model selection clustering for image data point using heuristic approach is compared with an existing Branch-and-Bound for Model Selection and Its Computational Complexity.
Figure 5 describes the computational complexity of identifying the models based on the data points of the given image. For a given data point, there might be different models based on different characteristics that need to be applied. Based on the characteristics of the problem, the user has to choose the model for a particular type of the process. In the proposed MSCHA, the process of selecting the model is based on the process of heuristics training sequences. The heuristic process followed trial and error process which formed a set of assumptions and

Table 1. No. of models vs. computational complexity.
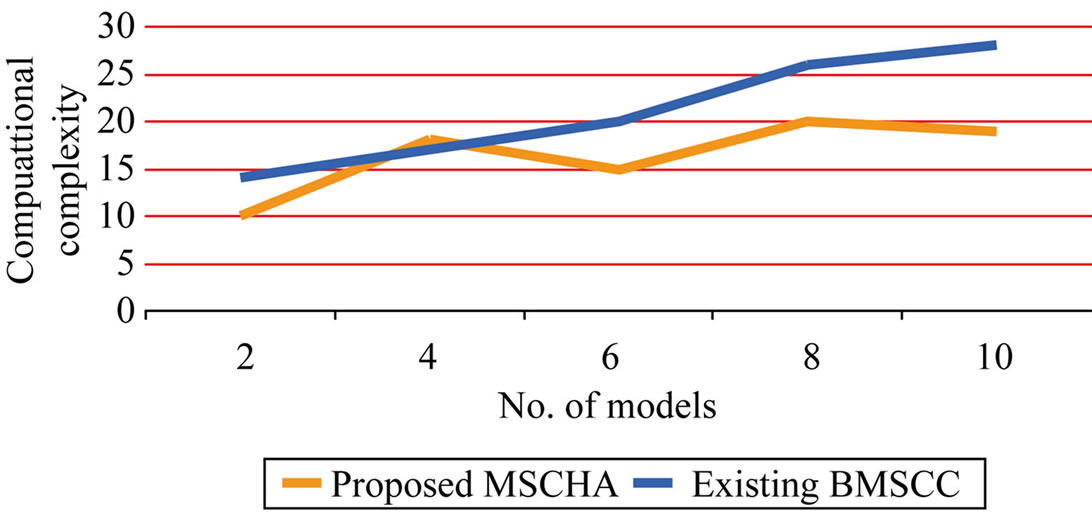
Figure 5. No. of models vs. computational complexity.
matched with the solution of the given problem. If it matched exactly, the technique stops its process. So, the computational complexity of the model selection process is considerably low in the proposed MSCHA compared to an existing BMSCC. The variance in computational complexity is 25% - 35% low in the proposed MSCHA.
The above Table 2 describes the detection rate of the best model formed based on the number of models to be formed with the given data point of the image. The detection arte of the proposed model selection clustering for image data point using heuristic approach is compared with an existing Branch-and-Bound for Model Selection and Its Computational Complexity.
Figure 6 describes the detection arte of the best model formed based on the number of models to be formed with the given data point of the image. For the given problem characteristics, we have to choose the model to resolve the given problem. In the proposed MSCHA, the process of choosing the model is done based on the trial and error procedure. Generate and test procedure will keep on forming the solution until the solution is exactly matched with the given problem characteristics. Compared to an existing Branch-and-Bound for Model Selection and Its Computational Complexity, the proposed MSCHA provides the best detection rate by consuming less interval of time. The variance in the detection rate of the proposed model selection clustering for image data point using heuristic approach is 20% - 30% low contrast to BMSCC.
The above Table 3 describes the time consumption of choosing the best model formed based on the number of models to be formed with the given data point of the image. The detection arte of the proposed model selection clustering for image data point using heuristic approach is compared with an existing Branch-and-Bound for Model Selection and Its Computational Complexity.
Figure 7 describes the time consumption of choosing the best model formed based on the number of models to be formed with the given data point of the image. The consumption of time is ensured based on the time taken to identify the best model with minimal number of trials. The time consumption is measured in terms of seconds. In the proposed MSCHA, the best solution is identified

Table 2. No. of models vs. detection rate of best model.

Table 3. No. of models vs. time consumption.
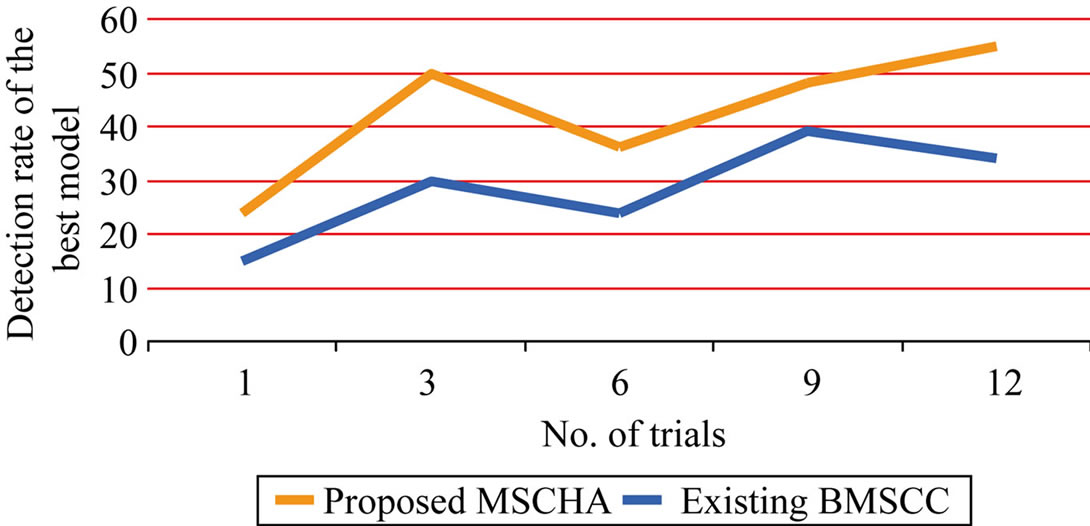
Figure 6. No. of models vs. detection rate of best model.

Figure 7. No. of models vs. time consumption.
in a less interval of time since it followed generate and test procedure. Trials are generated based on the models formed with the given data point. While generating the trials, it will check the solution with the given problem characteristics simultaneously, so the process consumes less time in the proposed MSCHA. Compared to an existing Branch-and-Bound for Model Selection and Its Computational Complexity, the proposed model selection clustering for image data point using heuristic approach consumes less time and the variance is 25% - 35% low in the proposed MSCHA.
Finally, it is being observed that the proposed MSCHA efficiently identified the best model for the data point of the given image through the process of heuristic training sequences on image data points and appropriate the problem-specific characteristics. Generate and test procedure is followed for identifying the best model criteria based on the specific problem characteristics in a less interval of time.
5. Conclusion
In this paper, we proposed a heuristic approach based model selection algorithm for clustering of image data to the given data points and examined its estimated difficulty. The proposed model-selection-based approach using heuristic notices the number of clusters routinely and it is vigorous to outliers. When compared to an existing branch and bound algorithm for model based clustering, the proposed MSCHA algorithm illustrates marked development in the time consumption, detection rate of selecting the best model among the set of models. It could also be observed from the experiments that the average complexity of the MSCHA algorithm is much lower than the BMSCC worst case complexity. Thus the proposed MSCHA algorithm is practical for model-based clustering of image data, which has reasonable number of training sequences, and processed based on the appropriate problem characteristics. With problem-specific bounds and/or added heuristics, the complexity of the proposed model selection clustering for image data point using heuristic approach algorithm can be further reduced. Even though the proposed MSCHA mechanism provides an appropriate model for specific characteristics of the problem, it does not identify the candidate attributes of the chosen model for data discovery in the dense data points of the image. The issue raised over data discovery in the dense data points of the image is carried efficiently in our future work.