A Family of Methods for Solving Nonlinear Equations with Twelfth-Order Convergence ()
1. Introduction
Solving nonlinear equations is one of the most important problems in numerical analysis. Generally，it is difficult to find the exact root of the nonlinear equations, and so iterative methods become the efficient way to obtain approximate solutions. Two important aspects related to iterative methods are order of convergence and computational efficiency. Order of convergence presents the speed at which a given iterative sequence converges to the root, and the computational efficiency shows the economy of the iterative scheme. In this paper, we will consider the above two aspects and establish a family of iterative methods to find the simple roots for the nonlinear equation
, i.e., we will find 
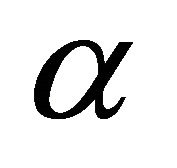such that
.
It is well known that the classical Newton’s method is a basic and important iterative method [1] to find 
by
which is quadratically convergent in the neighborhood of
.
In recent years, many variants of accelerated Newton’s methods have been proposed, for example [1-14]. In particular, [1,14] constructed a variant of Newton’s method via the iterative scheme:
which converges cubically with three function evaluations per iteration and the computational efficiency index 1.442. In [10], the authors presented a new modification of Jarratt’s method based on the circle of curvature which has the same convergent speed as our method.
Motivated by the recent activities in developing modified Newton’s method, concerning both the order of convergence and the computational efficiency, we present a family of new iteration schemes for solving nonlinear equations with twelfth-order convergence which are better than Newton’s method, the method provided by [1,10,14], and can be used to find the simple roots of any type of nonlinear equation
.
2. Convergence Analysis
Based on the iterative method provided by [1,14], we construct the iterative scheme as follows:
(1)
where 
and 
is an arbitrary real constant.
Theorem 2.1. Let 
be a simple root of sufficiently smooth function 
for an open interval
. If 
is sufficiently close to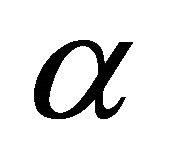
, then the method defined by (1) is at least twelfth-order , and its error equation is given by
(2)
where
.
Proof: By Taylor expansion of the function 
at point 
and using the fact that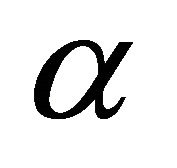 
is a simple zero of
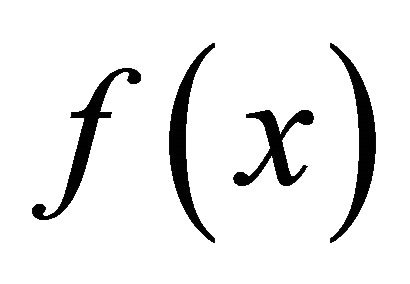, we have
and
Thus
and
Similarly, we have
and
Note that
and using the Taylor expansions of 
and
, we have
and
Hence,
and
Furthermore, we can obtain that
and
it follows from (1) that
that is
The proof is complete.
3. Numerical Examples
We give some examples to illustrate the efficiency of the new iterative method (1) with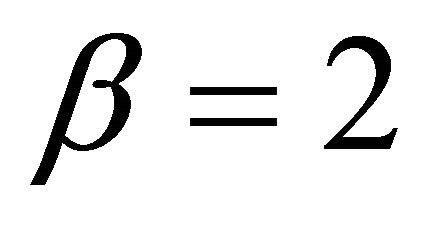 
(denoted by NVNM) and compare the method with Newton’s method (NM), the method provided by [1] (VNM), [10] (YM) and [14] (VNM).
We use the following stopping criteria for computer programs:
and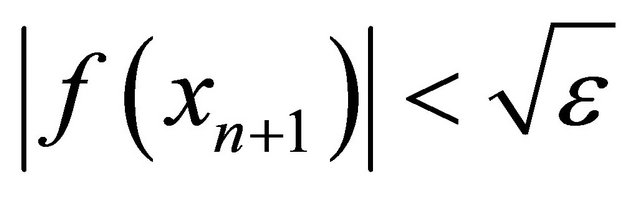
where
, which are the same as those used in [14].
The test functions are listed as follows:
The computational results in the Table 1 show that the method NVNM requires less NOFE than NM, and less NOFE than VNM in most cases. So, it is better in practical interest.
4. Conclusion
It is shown that the method (1) converges to the root. The computational efficiency index is 1.513 which is bigger than the index of NM 1.414 and the index of VNM 1.442. The method constructed in this paper is more efficient and performs better than classical Newton’s method and the method presented by [1,10,14].
Table 1. Comparison of some iterative methods.
N: Numbers of iterations; NOFE: Numbers of function evaluations.
5. Acknowledgements
This paper was supported by the NNSF (10961020), the Chunhui Project of Chinese Ministry of Education (Z2009-1-81007), the 135 Talent Project of Qinghai Province and the Foundation of the Chinese Nationality Committee (10QH03).