1. Introduction
In macrophysics mass (m) is defined as the measure of a particle’s resistance to acceleration, and is measured relative to a standard mass (ms); , where a is a dimensionless parameter. If a results from a purely mechanical interaction, m is called inertial mass (mi); and if from gravitational interaction, m is called gravitational mass s(mg). In the 19th century Roland Eotvos showed experimentally that
, where a is a dimensionless parameter. If a results from a purely mechanical interaction, m is called inertial mass (mi); and if from gravitational interaction, m is called gravitational mass s(mg). In the 19th century Roland Eotvos showed experimentally that . The particle used as a standard of mass is a 1-kg cylinder of platinum-iridium alloy, called the international standard of mass [1].
. The particle used as a standard of mass is a 1-kg cylinder of platinum-iridium alloy, called the international standard of mass [1].
In microphysics, on the other hand, the mass of a fundamental (elementary) particle is an intrinsic property of the particle—it is the measure of the amount of matter (or antimatter) in the particle. Defined in this way, mass is an absolute quantity! Experiments performed in the 20th century established that the elementary particle masses that are known range between zero and about 100 GeV [2].
The scientific method consists of two components, namely, the study of science based on observation and experience, and the study of science based on the mathematization of physical processes (theorization). The two components are not independent—a symbiotic relationship exists between them: A fundamental theory changes our view of the universe; it’s unifying synthesis joins two or more separate bodies of established knowledge whose connection at some deep level had not previously been recognized. Observations confirm the predictions of the new theory. On the other hand observations may form the basis of a new theory, and the theory confirms the observation, and in some cases extends and generalizes the observation.
The mass of elementary particles appears to be an exception to this symbiosis according to the two cornerstones of 20th century physics, standard model of elementary particles and the big-bang scenario: Gauge theory forbids masses for all the known elementary particles! For them to acquire masses, gauge symmetry must be broken simultaneously some way! The symmetry of gauge theory will be spontaneously broken if some gauge noninvariant scalar quantity is non-zero in the theory’s lowest energy state. The original version of the standard model introduced a new elementary scalar particle, called the Higgs particle, to make gauge invariance break down spontaneously. The Higgs particle’s couplings to other particles are proportional to their masses, and are hence fixed though unexplained [2]. The disciples of the standard model announced the discovery of the Higgs particle of mass greater than 100 GeV on 4th July, 2012. This result is in violent disagreement with experiment.
The problem of the disciples of the big-bang scenario is not the determination of the masses of elementary particles, but rather the asymmetry between matter and antimatter; and whether the asymmetry has a cosmic origin or whether it results from cosmic evolution. Thus, given the assumed expansion of the universe, what is the universe’s ultimate fate-whether it will expand indefinitely, or it will terminate eventually and thereafter remain static, or the expansion will stop and then be followed by recollapse? The answer depends on the critical mass density (rc) of the universe. rc is the density required to close the universe—that is for its own gravitational self-attraction to be sufficient to terminate the current expansion eventually, or to stop the expansion and cause recollapse. If the density (r) of the universe is less than rc then the universe will expand for ever.
The present baryon density (rb) is one or two orders of magnitude less than rc, hence rb is insufficient to close the universe. This is the problem of the invisible (or missing, or dark) matter, which is assumed to be something other than baryons. The dark-matter candidates must be nonbaryonic dark-mass and together with baryonic dark-mass the closure density can be achieved. Several elementary particles, some yet unobserved, are proposed as dark-matter candidates including massive neutrinos, axions, photino, gravitino, etc. Arguments from cosmology have set a rough upper limit of a few GeV on the neutrino mass, based on the observation that the universe is still expanding at present, if these neutrinos are not to decelerate or reverse the expansion of the universe. These constraints on the neutrino masses are much more general than those obtained from laboratory experiments according to which the most stringent upper limit on a neutrino mass is about 10−4 of the electron mass for the electron neutrino. Other dark-matter candidates can have any mass whatsoever [3].
The assumed matter-antimatter asymmetry is in conflict with the Dirac theory of the electron, a special case. There is complete symmetry between electrons and positrons in the Dirac theory [4]. Dirac’s theory is a proof that the assumed matter—antimatter asymmetry does not apply in the fermion world. Dirac’s proof has now been extended to all physical worlds [5]. Thus, the assumed mater-antimatter asymmetry is not a law of nature! Further, the conclusion that non-baryonic elementary particles can have any mass is in conflict with the experimentally established fact that elementary particle masses range between zero and about 100 GeV. Finally, the universe is not undergoing any motion relative to us, if it did we cannot detect it because we are part of the universe—no absolute motion.
2. The Mass of an Elementary Particle
Every elementary particle has a dual nature, namely, particle and wave properties. The particle variables E (energy) and  (momentum) are connected by the fundamental relation [4],
(momentum) are connected by the fundamental relation [4],
 (1)
(1)
where m is the rest mass of the particle, while the wave variables l (wave length) and n (frequency) are related to the particle variables by the Louis de Broglie equations,
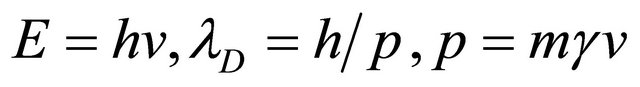 (2)
(2)
where h is Planck’s constant, v the speed of the particle, g the Einstein factor, and lD the de Broglie wave length [6]. It is clear from (2) that lD is not defined in the special cases v = 0, and v = c. These special cases describe two fundamental particles, namely, the photon with v = c, and graviton with v = 0—the photon is a particle with no corresponding antiparticle, and the graviton is an antiparticle with no corresponding particle [5]. From (1) and (2) we deduce that when v = c, corresponding to m = 0,  , and when v = 0,
, and when v = 0, 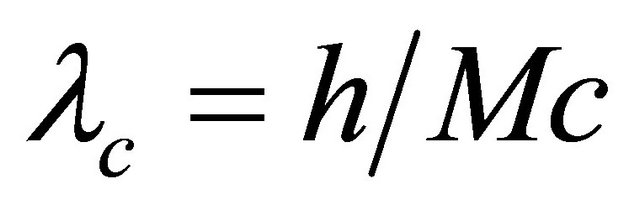 , where
, where  is Compton wavelength, and M is the mass of the graviton.
is Compton wavelength, and M is the mass of the graviton.
Consider now the ratio , where m is the mass of all other elementary particles of nature. A plot of y against v gives a straight line of slope
, where m is the mass of all other elementary particles of nature. A plot of y against v gives a straight line of slope  passing through the origin. When g = 1 corresponding to v = 0, m = M and
passing through the origin. When g = 1 corresponding to v = 0, m = M and ; and when g = c corresponding to g = ¥, m = o. Hence the allowed masses are those for which
; and when g = c corresponding to g = ¥, m = o. Hence the allowed masses are those for which , so that as g®¥,m®o. Thus, M is the mass standard for elementary particles and elementary particle masses are defined relative to the mass of the graviton and their normalized values lie between zero and 1. Exact theory shows that M is the mass of the Z0, hence Z0 is the graviton and not a weakly interacting nuclear particle [5].
, so that as g®¥,m®o. Thus, M is the mass standard for elementary particles and elementary particle masses are defined relative to the mass of the graviton and their normalized values lie between zero and 1. Exact theory shows that M is the mass of the Z0, hence Z0 is the graviton and not a weakly interacting nuclear particle [5].
3. The Neutrino Mass
Wulfgang Pauli proposed the existence of neutrinos in 1930 while investigating the conundrum of radioactive beta decay. He hypothesized, in order to abide by the laws of energy conservation, the existence of as yet undetected neutral particle which Enrico Fermi named “neutrino” (“little neutral one”). About his hypothesis, Pauli wrote “I have done something very bad today by proposing a particle that cannot be detected; it is something no theorist should ever do.” It became clear that if such a particle existed, it must be both very light and interact very weakly with matter, making it difficult to detect.
In 1956, however, Clyde Cowan and Frederic Reines succeeded in detecting the electron neutrino. On getting the information about neutrino’s detection, Pauli retorted “Everything comes to him who knows how to wait.” The discovery of the electron neutrino was followed in 1962 by the discovery of the muon neutrino corresponding to the charged muon lepton; and that of the tau neutrino on July 21, 2000, corresponding to the charged tau lepton [7].
The discovery of the neutrinos raise some fundamental questions: whether neutrinos might have a tiny bit of mass, whether they could oscillate, and how many kinds of neutrinos exist? On the basis of the big bang scenario stable neutrino mass must be less than 100eV, or more than a few GeV. Laboratory experiments, on the other hand, posit that electron neutrino mass is about 10−4 of the electron mass. Nucleosynthesis impose the most stringent limit on the number of neutrino species—the number is restricted to 3 or at most 4 which is below the best upper limits available from particle physics experiments. Formal theory gives 3 as the number of neutrino species, all of which are stable [5]. Thus, the neutrino mass is the only outstanding problem that needs to be settled.
This problem can be settled on the basis of the geometrical theory of the chemical elements; according to which fermions reside in 4n-dimensional reducible quantum spaces —n is the index of the space and is called principal quantum number and period by physicists and chemists respetively [5]. The implication of this is that each fermion system (neutrinos, electrons, protons, neutrons and their antiparticles) reside in an infinite set of discrete energy levels separated by energy gap En = hn, where n is the Lamb-Retherford frequency (n = 1000 megahertz), and h the Planck’s constant—n is the frequency of a microwave field that induced transitions between the two levels of the hydrogen atom. Thus, the energy quantum hn is the work done by an external field to “lift” the electron from one atomic level to the neighbouring level (the electron loses this quantum of energy to return to the original level when the field is removed). This gives a gap “width”
—n is the index of the space and is called principal quantum number and period by physicists and chemists respetively [5]. The implication of this is that each fermion system (neutrinos, electrons, protons, neutrons and their antiparticles) reside in an infinite set of discrete energy levels separated by energy gap En = hn, where n is the Lamb-Retherford frequency (n = 1000 megahertz), and h the Planck’s constant—n is the frequency of a microwave field that induced transitions between the two levels of the hydrogen atom. Thus, the energy quantum hn is the work done by an external field to “lift” the electron from one atomic level to the neighbouring level (the electron loses this quantum of energy to return to the original level when the field is removed). This gives a gap “width”  , and is the same for the electron neutrino.
, and is the same for the electron neutrino.
The neutrino is affected by the gravitational force which is 10−36 times weaker than the electromagnetic force, hence , where
, where  is the energy the charged lepton loses when it returns to the original level. On putting
is the energy the charged lepton loses when it returns to the original level. On putting  and substituting the values of the fundamental constants we obtain,
and substituting the values of the fundamental constants we obtain,
 (3)
(3)
These neutrino masses are so small that their experimental determination lies in the distant future on account of the sensitivity of today’s instruments.
4. Conclusion
Conventionally elementary particle is a particle that is not composite-hence elementary particles are the simplest physical objects in the universe. This is certainly necessary but not sufficient; rather, we define elementary particle as a particle of spin  and rest mass m which is subject to the constraint
and rest mass m which is subject to the constraint . Thus, in unit of the mass of the graviton, 0 £ m £ 1. Elementary particles of spin (rank) 0 and
. Thus, in unit of the mass of the graviton, 0 £ m £ 1. Elementary particles of spin (rank) 0 and  are stable, being residents of irreducible “tensor spaces”, and elementary particles of spin (rank) 1 are unstable because eventhough the base “space” is irreducible they cannot on their own form physical states. Thus, fermions and bosons of spin zero (photon and graviton) are stable, while the Ws and mesons are unstable [5].
are stable, being residents of irreducible “tensor spaces”, and elementary particles of spin (rank) 1 are unstable because eventhough the base “space” is irreducible they cannot on their own form physical states. Thus, fermions and bosons of spin zero (photon and graviton) are stable, while the Ws and mesons are unstable [5].
Einstein’s theory of gravitation (General Theory of Relativity (GTR)) was formulated by analogy with electromagnetism: Electromagnetism is described by a 4- tensor Fmn which is derivable from a 4-vector Am, a purely physical quantity [8]. On the other hand Einstein’s gravitation is described by a symmetric 4-tensor gmn, a purely geometrical entity, which is a function of the space-time variables. gmn is not derivable from any 4-vector, indeed the gravitational 4-vector analogous to Am is a purely static entity, and hence not a function of the time [9]. Gravitation being a time-independent phenomenon is not described by Einstein’s 4-tensor (gmn). Consequently Einstein’s theory of general relativity is not a theory of gravitation; hence its consequences, gravitational radiation, black holes, quantum gravity, etc. have nothing to do with physical reality! As a physical theory GTR is a massive blunder, but as a geometrical theory of curved space-time it is a thing of exquisite beauty.
According to the big bang scenario the universe evolved from an undefined initial state via an explosion of a hot, dense mixture of matter and energy. As a consequence of this cosmic explosion the universe is expanding and this expansion is buoyed up by the matter-antimatter asymmetry (dark energy). The fate of the universe depends on its mass density: If the mass density r = pc, the expansion will either stop so that the universe is closed and static, or stop and contract, where rc is the closure density. The observed present density r is less than rc, hence for the universe to be closed there must exist unobserved density, called the invisible (missing, or dark) matter, to ensure this closure. The arbitrary initial state is in conflict with the principle of relativity because it violates the dimensionality law of nature, and the assumed matter-antimatter asymmetry is inconsistent with the established matter-antimatter symmetry in the universe [5]. Consequently the big bang scenario is not a theory of the universe!