Pricing and Hedging in Stochastic Volatility Regime Switching Models ()
1. Introduction
In this paper, we consider general regime switching stochastic volatility models where both the asset and the volatility dynamics depend on the values of a Markov jump process. We are interested in finding formulae to solve the problem of pricing and hedging contingent claims in this framework. However, due to the stochastic volatility and the Markov regime switching, the market is incomplete and thus perfect pricing and hedging are not possible. Hence, to hedge derivatives, we adopt firstly the local-risk minimization approach studied by Föllmer and Schweizer in [1]. This approach consists of controlling the hedging errors at each instant  by minimizing the conditional variances of the instantaneous cost increments. Health et al. in [2], provided comparative theoretical and numerical results on risks, values and hedging strategies for this approach versus the meanvariance (see [3] or [4] for more details on this approach), in the specific case of stochastic volatility models. We propose in this paper to apply the local risk minimization approach to a more global class of stochastic volatility models since we will assume in the sequel that all parameters of the model depend on the values of a Markov jump process. Hence, we will work on a global class of regime switching stochastic volatility models. We will obtain formulae to give the price of contingent claims by solving a system of partial differential equations. We will also obtain the optimal strategy which solves the local risk minimization hedging problem.
by minimizing the conditional variances of the instantaneous cost increments. Health et al. in [2], provided comparative theoretical and numerical results on risks, values and hedging strategies for this approach versus the meanvariance (see [3] or [4] for more details on this approach), in the specific case of stochastic volatility models. We propose in this paper to apply the local risk minimization approach to a more global class of stochastic volatility models since we will assume in the sequel that all parameters of the model depend on the values of a Markov jump process. Hence, we will work on a global class of regime switching stochastic volatility models. We will obtain formulae to give the price of contingent claims by solving a system of partial differential equations. We will also obtain the optimal strategy which solves the local risk minimization hedging problem.
There has been considerable interest in applications of regime switching models driven by a Markov process to various financial problems. Elliott et al. in [5] provided an overview of hidden Markov chain models. Indeed, the use of Markov switching in diffusions allows us to have different levels of drift or volatility during time. Moreover these regime switching activities are a better fit for economic times series data than non regime switching models and also allow us to better capture some market features or economics behaviors such as recession and financial crisis periods (see for example Goutte and Zou in [6]). Thus, Di Masi et al. in [7] considered the problem of hedging an European call option for a (nonstochastic volatility) diffusion models where the drift and volatility are functions of a Markov jump process.
Furthermore, we are also interested in pricing volatility derivatives, such as variance and volatility swaps. Broadie et al. in [8] studied the pricing and hedging of variance swaps and other volatility derivatives in the classical Heston stochastic volatility model introduced by Heston in [9]. Elliott et al. in [10] then developed a model for pricing the same class of derivatives but under a Markov-modulated version of this stochastic volatility model. In their paper, they only considered the case where not all the parameters of the model depend on the state of the Markov process. Moreover, they studied only the Heston stochastic volatility model. Hence, based on these two preceding works, we will extend this methodology to our global class of regime switching stochastic volatility models. Thus, we will obtain formulae to price options on the stochastic volatility process such as variance and volatility swaps.
This paper is arranged as follows: Section 1 gives the notion of the regime switching framework and presents our regime switching stochastic volatility models. Section 2 solves the problem of pricing and hedging using the local risk minimization approach. Section 3 then gives the formulas to price options on the volatility process.
2. The Stochastic Regime Switching Volatility Model
Let  be a filtered probability space with filtration
be a filtered probability space with filtration  satisfying the usual conditions for some fixed but arbitrary time horizon
satisfying the usual conditions for some fixed but arbitrary time horizon . We consider a general stochastic volatility model defined by the stochastic differential equations:
. We consider a general stochastic volatility model defined by the stochastic differential equations:
 (1.1)
(1.1)
where  and
and  are two correlated Brownian motions. In fact, the process
are two correlated Brownian motions. In fact, the process  represents the discounted price process of a tradable asset price process
represents the discounted price process of a tradable asset price process 
divided by a Bond price process . The process
. The process
 represents the savings account in a riskless asset.
represents the savings account in a riskless asset.
 is a real stochastic process which is
is a real stochastic process which is  adapted and
adapted and  is a Markov jump process on finite state space
is a Markov jump process on finite state space . It can be viewed as an observable exogenous quantity. We assume that the time invariant matrix
. It can be viewed as an observable exogenous quantity. We assume that the time invariant matrix  denotes the infinitesimal generator
denotes the infinitesimal generator  of
of , where
, where  is an infinitesimal intensity of
is an infinitesimal intensity of . This generator is defined as
. This generator is defined as , for all
, for all  and
and  for all
for all .
.
Then, the semi-martingale decomposition for  is given by
is given by

where  is an
is an  -valued martingale with respect to
-valued martingale with respect to , which is the natural filtration generated by the Markov process
, which is the natural filtration generated by the Markov process  under
under .
.
Hence, in our model, there are three sources of randomness: ,
,  and
and . We will denote by
. We will denote by
 the filtration generated by the two Brownian motions. Finally, we will denote by
the filtration generated by the two Brownian motions. Finally, we will denote by  the global filtration
the global filtration .
.
Let  be the sequential jump times of
be the sequential jump times of  (i.e.
(i.e. ) and
) and  a jump measure of
a jump measure of , i.e. the integer-valued random measure given by
, i.e. the integer-valued random measure given by
 (1.2)
(1.2)
Then the  -compensator of
-compensator of  is given by
is given by
 (1.3)
(1.3)
Assumption 1.1
1) We assume all the hypothesis to ensure the existences and the regularities of the solutions of our model (1.1) (see for example [11] for more details). Hence, the system of stochastic differential Equations (1.1) admits a unique strong continuous solution for the vector process  with a strictly positive price process
with a strictly positive price process  and a volatility process
and a volatility process .
.
2) We assume moreover that the Markov process  is independent to both processes
is independent to both processes  and
and .
.
Remark 1.1 This independence implies that the Markov process  is an exogenous factor of the market information. Thus, it can be viewed as an exogenous factor such as an economic impact factor. An economic interpretation of this is that this Markov process can represent a credit rating of a firm
is an exogenous factor of the market information. Thus, it can be viewed as an exogenous factor such as an economic impact factor. An economic interpretation of this is that this Markov process can represent a credit rating of a firm . Indeed, assume that our stochastic volatility model describes the price of a commodity produced by the firm
. Indeed, assume that our stochastic volatility model describes the price of a commodity produced by the firm , then the Markov process
, then the Markov process  can represent the credit rating of this firm given by an exogenous rating company as “Standard and Poors”. Thus, it is natural to think that the dynamic of the commodity’s price, produced by the firm
can represent the credit rating of this firm given by an exogenous rating company as “Standard and Poors”. Thus, it is natural to think that the dynamic of the commodity’s price, produced by the firm , depends on the value of this notation
, depends on the value of this notation .
.
To exclude arbitrage opportunities, we assume that the process S admits an equivalent local martingale measure (ELMM) . In the sense that it is a probability measure with the same null sets as
. In the sense that it is a probability measure with the same null sets as  and such that the process S is a local martingale under
and such that the process S is a local martingale under . We will denote, in the sequel, by
. We will denote, in the sequel, by  the set of all ELMMs
the set of all ELMMs .
.
Remark 1.2
1) We can rewrite the Brownian motion  as
as  , where the process
, where the process  is another Brownian motion such that processes
is another Brownian motion such that processes  and
and  are now independent.
are now independent.
2) The condition that S should be a  -local martingale fixes the effect of the Girsanov transformation of
-local martingale fixes the effect of the Girsanov transformation of  but allows us for different transformations on the independent Brownian motion
but allows us for different transformations on the independent Brownian motion  defined in point 1. Consequently, if the correlation factor
defined in point 1. Consequently, if the correlation factor  satisfies
satisfies , then the set
, then the set  contains more than one element and so the financial market is then incomplete. Moreover, there is an other source of incompleteness of the market which is the dependence of processes
contains more than one element and so the financial market is then incomplete. Moreover, there is an other source of incompleteness of the market which is the dependence of processes  and
and  with respect to the Markov process
with respect to the Markov process .
.
We give now some examples of classical stochastic volatility models which are contained in our model (1.1).
Example 1.1 Hull-White:



Stein-Stein:



Heston:




3. Pricing and Hedging via Local Risk Minimization Approach
We are interested, in this section, in the hedging of an European contingent claims with an  -measurable squared integrable random variable
-measurable squared integrable random variable  based on the dynamics given by (1.1). As an example of this payoff, we can take an European call option:
based on the dynamics given by (1.1). As an example of this payoff, we can take an European call option:  with maturity T and strike K > 0.
with maturity T and strike K > 0.
We consider here the local risk-minimization approach to hedge in this incomplete market. We recall some definitions of this approach.
Definition 2.1 An hedging strategy is a pair  such that
such that  is a predictable process which satisfies
is a predictable process which satisfies
 (2.4)
(2.4)
and  is an adapted process such that
is an adapted process such that
 (2.5)
(2.5)
We will denote by  the set of strategies which satisfy (2.4) and (2.5).
the set of strategies which satisfy (2.4) and (2.5).
The hedging strategy  defines a portfolio where
defines a portfolio where  denotes the number of shares of the risky asset
denotes the number of shares of the risky asset  held by the investor at time
held by the investor at time  and
and  denotes the amount invested at time
denotes the amount invested at time  in the bond.
in the bond.
Definition 2.2 Given a hedging strategy , we call the Value process
, we call the Value process  of this corresponding portfolio the right continuous process given by
of this corresponding portfolio the right continuous process given by
 (2.6)
(2.6)
Definition 2.3 Given a hedging strategy , we call the Cost process
, we call the Cost process  of this corresponding portfolio the process given by
of this corresponding portfolio the process given by
 (2.7)
(2.7)
We can see that the quantity  represents the hedging gains or losses up to time
represents the hedging gains or losses up to time  following the hedging strategy
following the hedging strategy . A hedging strategy
. A hedging strategy  is called self-financing if its cost process is
is called self-financing if its cost process is  -a.s. constant over the time
-a.s. constant over the time  and mean self-financing if
and mean self-financing if  is a
is a  -martingale. If
-martingale. If  is square integrable, then the risk process of
is square integrable, then the risk process of  is defined by
is defined by
 (2.8)
(2.8)
Remark 2.3 Since the contingent claim  is
is  - measurable and
- measurable and  is adapted, there always exists a hedging strategy such that
is adapted, there always exists a hedging strategy such that . Indeed, we can take
. Indeed, we can take  and
and  for all
for all .
.
3.1. Local Risk Minimization Approach
We only consider hedging strategies which replicate contingent claim  at time
at time . This means that we only allow hedging strategies
. This means that we only allow hedging strategies  such that
such that
 (2.9)
(2.9)
Thus, the hedging problem is so to find the strategy  which minimizes at time
which minimizes at time  the quadratic risk:
the quadratic risk:
 (2.10)
(2.10)
The idea is so to control the hedging errors at each instant  by minimizing the conditional variances of the instantaneous cost increments sequentially over time.
by minimizing the conditional variances of the instantaneous cost increments sequentially over time.
Remark 2.4 An alternative approach to hedge in incomplete market is the mean-variance approach (see [3]). In fact, in this approach, the aim is to minimize the global risk over the entire time . Hence, it is a different approach than the local risk minimization which focuses on the minimization of the second moments of the infinitesimal cost increments (8).
. Hence, it is a different approach than the local risk minimization which focuses on the minimization of the second moments of the infinitesimal cost increments (8).
Therefore, the study of this minimization problem in a general semimartingale case is due to Schweizer [3] and it requires more assumptions on the asset dynamic . We assume firstly that
. We assume firstly that  can be decomposed as
can be decomposed as

where  is a real valued locally squared integrable local
is a real valued locally squared integrable local  -martingale null at zero and A is a real valued adapted continuous process of finite variation also null at zero.
-martingale null at zero and A is a real valued adapted continuous process of finite variation also null at zero.
We recall now the Definition of the Structure Condition (SC). We say that the process  satisfies the (SC) if there exists a predictable process
satisfies the (SC) if there exists a predictable process  such that the process
such that the process  is absolutely continuous with respect to
is absolutely continuous with respect to  (i.e. the oblique bracket). In the sense that
(i.e. the oblique bracket). In the sense that

and such that the so called mean variance tradeoff process (MVT)  satisfies
satisfies

Lemma 2.1 Since , we have that if the process
, we have that if the process  is continuous then (SC) is satisfied.
is continuous then (SC) is satisfied.
Proof. See Theorem 1 of Schweizer [4].
Proposition 2.24 of Föllmer and Schweizer in [1] shows that finding a locally risk minimizing strategy for a given contingent claim  is equivalent to finding a decomposition of
is equivalent to finding a decomposition of  of the form:
of the form:
 (2.11)
(2.11)
where  is a constant,
is a constant,  is a predictable process satisfying Condition (2.4) and
is a predictable process satisfying Condition (2.4) and  is a square integrable
is a square integrable  -martingale null at 0 and strongly orthogonal to
-martingale null at 0 and strongly orthogonal to  (i.e.
(i.e.  is a P-martingale). The representation (2.11) is usually referred to as the Föllmer-Schweizer (FS) decomposition of the random variable
is a P-martingale). The representation (2.11) is usually referred to as the Föllmer-Schweizer (FS) decomposition of the random variable . Once we have (2.11), then the desired hedging strategy
. Once we have (2.11), then the desired hedging strategy , which is locally risk minimizing, is then given, for all
, which is locally risk minimizing, is then given, for all , by
, by
 (2.12)
(2.12)
and
 (2.13)
(2.13)
where
 (2.14)
(2.14)
with
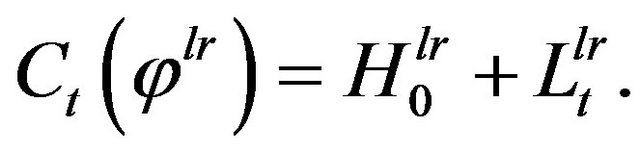 (2.15)
(2.15)
In view of these results, finding the Föllmer-Schweizer decomposition (2.11) of a given contingent claim  is important because it allows us to obtain the locally risk minimizing strategy. Monat and Sticker in [12] and Pham et al. in [13] give sufficient conditions to prove the existence of this decomposition. We therefore explain how one can often obtain this decomposition by switching to a suitably chosen martingale measure for S. Indeed, as it is shown in [1] and [4], there exists a measure
is important because it allows us to obtain the locally risk minimizing strategy. Monat and Sticker in [12] and Pham et al. in [13] give sufficient conditions to prove the existence of this decomposition. We therefore explain how one can often obtain this decomposition by switching to a suitably chosen martingale measure for S. Indeed, as it is shown in [1] and [4], there exists a measure , which is the so called minimal equivalent local martingale measure (minimal ELMM), such that
, which is the so called minimal equivalent local martingale measure (minimal ELMM), such that
 (2.16)
(2.16)
where  denotes the conditional expectation under
denotes the conditional expectation under .
.
Remark 2.5 If there exists a locally risk minimizing strategy , then we can use the expression of
, then we can use the expression of  appearing in (2.16) as a price of the contingent claim
appearing in (2.16) as a price of the contingent claim  at time
at time .
.
In the case where the process  is continuous (which is our case), Theorem 1 of [1] allows us to construct uniquely
is continuous (which is our case), Theorem 1 of [1] allows us to construct uniquely . Indeed, we have the following result:
. Indeed, we have the following result:
Proposition 2.1  exists if and only if for all
exists if and only if for all 
 (2.17)
(2.17)
is a square integrable martingale under .
.
Moreover,  defines a probability measure
defines a probability measure  equivalent to
equivalent to  which is in
which is in  since one easily verifies that
since one easily verifies that  is a local
is a local  -martingale.
-martingale.
3.2. Markovian Regime Switching Case
Let ,
,  and
and  given by the model (1.1), then the local risk minimizing hedging strategy can be obtained in two steps:
given by the model (1.1), then the local risk minimizing hedging strategy can be obtained in two steps:
1) Determine  and deduce the dynamic of
and deduce the dynamic of  under
under .
.
2) Find the Galtchouk-Kunita-Watanabe decomposition of  with respect to
with respect to 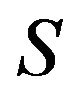 under
under .
.
Then, the optimal local risk minimizing hedging strategy is given by (2.12) and (2.13).
3.2.1. Finding 
According to the previous subsection, the density process of the minimal ELMM  with respect to
with respect to  is given by the Equation (2.17). We can firstly remark that
is given by the Equation (2.17). We can firstly remark that

Since  is continuous, we have first of all to determine the canonical decomposition
is continuous, we have first of all to determine the canonical decomposition

of the asset process  under
under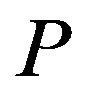 .
.
Proposition 2.2 Assume that the regime stochastic volatility model follows (1.1) then we have, for all , that
, that


therefore we obtain

Proof. It comes immediately from the definition of the dynamic of our model (1.1).
We are now able to determine the dynamic of our model under .
.
Proposition 2.3 Assume that  is a true
is a true  -martingale, then the dynamic of the model (1.1) under
-martingale, then the dynamic of the model (1.1) under  is given for all
is given for all  by
by
 (2.18)
(2.18)

with
 (2.19)
(2.19)
Proof. Since  is a
is a  -martingale, Girsanov’s theorem implies that
-martingale, Girsanov’s theorem implies that  and
and
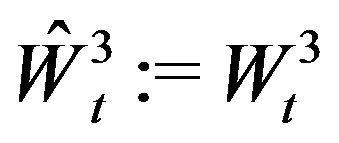 are independent
are independent  -Brownian motions. Hence
-Brownian motions. Hence

and

3.2.2. Decomposition of the Contingent Claim  with Respect to
with Respect to  under
under 
Let  be a contingent claim of the form
be a contingent claim of the form  , then finding the Galtchouk-KunitaWatanabe decomposition of
, then finding the Galtchouk-KunitaWatanabe decomposition of  under
under  reduces to solve a system of partial differential equations if one exploits the Markovian structure. Indeed, using the Markov property, we can rewrite (2.16):
reduces to solve a system of partial differential equations if one exploits the Markovian structure. Indeed, using the Markov property, we can rewrite (2.16):

for some function  defined on
defined on .
.
Proposition 2.4 For all , if
, if , then
, then  is the solution to the system of partial differential equations given by
is the solution to the system of partial differential equations given by
 (2.20)
(2.20)
with terminal condition for all  given by
given by
 and where
and where ,
,
 ,
,  ,
,  and
and .
.
Proof. Since

(2.21)
and notice that for any function  on
on  , which is right continuous and with left limits in
, which is right continuous and with left limits in , we have
, we have

Hence, replacing the last equality in (2.21) gives

The function  is a
is a  -martingale so all boundary terms are null. Hence we obtain that
-martingale so all boundary terms are null. Hence we obtain that  need to satisfy
need to satisfy

with terminal condition . Moreover,
. Moreover,

where  means that at time
means that at time  the Markov process is in state
the Markov process is in state  (i.e.
(i.e. ). Hence with
). Hence with , we obtain the expected result.□
, we obtain the expected result.□
Example 2.2 (Pricing European call options on the underlying process S) The value of an European call option on the stock price  with maturity T and strike K is given by
with maturity T and strike K is given by . Hence we can apply Proposition 2.4 with
. Hence we can apply Proposition 2.4 with

where the terminal conditions for all  are given by
are given by .
.
According to (2.12) and (2.15), we are now able to find the decomposition of  with respect to
with respect to  under
under  and so the locally risk minimizing
and so the locally risk minimizing  -admissible strategy
-admissible strategy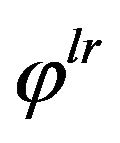 .
.
Theorem 2.1 For all , we have that the locally risk-minimizing hedging strategy of
, we have that the locally risk-minimizing hedging strategy of ,
,  is given by
is given by
 (2.22)
(2.22)
 (2.23)
(2.23)
where

and

Remark 2.6 Moreover, taking the problem at time , we get
, we get

which is the so-called Föllmer-Schweizer decomposition of the random variable .
.
Proof. Let , apply Ito’s formula to
, apply Ito’s formula to  , then by (2.21), we obtain:
, then by (2.21), we obtain:

We apply now the result of Proposition 2.4 to obtain

Combining this result with
 gives the expected result.□
gives the expected result.□
We can also obtain a formulation of the conditional expected squared cost on the time interval  for the locally risk-minimizing strategy
for the locally risk-minimizing strategy .
.
Proposition 2.5 We have, for all , that the conditional expected squared cost on the interval
, that the conditional expected squared cost on the interval  for the locally risk-minimizing strategy
for the locally risk-minimizing strategy  is given by
is given by

Proof. Applying the result of Theorem 2.1 in (2.8) we obtain

We can also simplify the second expectation

To apply all the results about local risk minimizing hedging strategy , it remains to prove that  is a true P-martingale and square integrable under P. A wellknown sufficient condition for both is the boundedness of the mean variance tradeoff process
is a true P-martingale and square integrable under P. A wellknown sufficient condition for both is the boundedness of the mean variance tradeoff process , stated in Proposition 0.2, uniformly in
, stated in Proposition 0.2, uniformly in  and
and  (see [12-14]).
(see [12-14]).
Proposition 2.6 If the mean variance tradeoff process , defined in Proposition 0.2, is uniformly bounded in
, defined in Proposition 0.2, is uniformly bounded in  and
and  then we have that:
then we have that:
1)  is a true
is a true  -martingale and square integrable under
-martingale and square integrable under .
.
2) H admits a Föllmer-Schweizer decomposition given by (2.11).
3) , defined in (2.12) and (2.13), is the local risk minimizing hedging strategy.
, defined in (2.12) and (2.13), is the local risk minimizing hedging strategy.
Example 2.3 (Heston model) We can take for the model (1.1) a Heston model case. Hence, by Example 1.1, we take




The constants ,
,  and
and  are all nonnegative for all
are all nonnegative for all . And we assume for the existence and positivity of the solution
. And we assume for the existence and positivity of the solution  that for all
that for all ,
,
 .
.
The model is then given by


and the corresponding mean variance tradeoff process is then given by

Hence the MVT process K is deterministic so bounded uniformly in  and
and . This implies that
. This implies that  is a P-martingale and so that we can apply all the results mentioned before.
is a P-martingale and so that we can apply all the results mentioned before.
4. Pricing Option on the Volatility: 
We are now interested in establishing some formulae to price options based on the stochastic volatility process .
.
4.1. Variance Swap
A variance swap is a forward contract on the annualized variance, which is the square of the realized annual volatility. Thus, let  denote the realized annual stock variance over the life of the contract. Then it is given by:
denote the realized annual stock variance over the life of the contract. Then it is given by:
 (3.24)
(3.24)
Let  and
and  denote the delivery price for variance and the notional amount of the swap in dollars per annualized volatility point squared. Then, the payoff
denote the delivery price for variance and the notional amount of the swap in dollars per annualized volatility point squared. Then, the payoff  of the variance swap at the maturity time
of the variance swap at the maturity time  is given by
is given by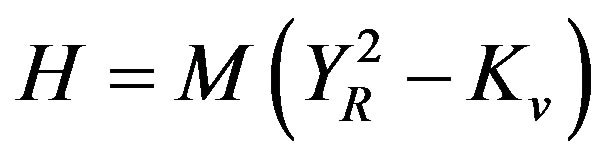 . Intuitively, the buyer will receive
. Intuitively, the buyer will receive  dollars for each point by which the realized annual variance
dollars for each point by which the realized annual variance  has exceeded the variance delivery price
has exceeded the variance delivery price . The results provided, in the sequel, are an extension of the results obtained in [10]. Indeed, firstly we study more general class of stochastic volatility models and secondly we apply our results, in the particular case of Heston model, but where not only the long-term volatility level depends on the regime but also the speed of mean reversion on the volatility of the volatility.
. The results provided, in the sequel, are an extension of the results obtained in [10]. Indeed, firstly we study more general class of stochastic volatility models and secondly we apply our results, in the particular case of Heston model, but where not only the long-term volatility level depends on the regime but also the speed of mean reversion on the volatility of the volatility.
Hence, we start by considering the evaluation of the conditional price of a derivative H given the information about the sample path of the Markov process from time 0 to time T (i.e. ). This means that we assume to know all the historical path of the Markov process
). This means that we assume to know all the historical path of the Markov process . Assume, also, that we are under the minimal ELMM
. Assume, also, that we are under the minimal ELMM . Thus, we recall that in this case our regime switching model is given by:
. Thus, we recall that in this case our regime switching model is given by:


with
 . In particular, given
. In particular, given , the conditional price of the variance swap
, the conditional price of the variance swap  is given by
is given by
 (3.25)
(3.25)
Hence, if we denote as previous
 , we obtain by Itô formula that for all
, we obtain by Itô formula that for all ,
,
 (3.26)
(3.26)
Thus, given , we get
, we get
 (3.27)
(3.27)
So
 (3.28)
(3.28)
Assumption 3.2 Assume that we know the solution of Equation (3.28) which we will denote by , for all
, for all .
.
Proposition 3.7 Under Assumption 3.2, we have, for all , that the conditional variance swap price P(X) is given by
, that the conditional variance swap price P(X) is given by
 (3.29)
(3.29)
Example 3.4 (Heston Model) Assume that we are in the Heston model case. Hence as mentioned in Example 1.1 we take
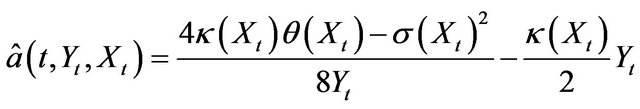
and

Then the dynamic of  is given by
is given by
 .
.
Moreover, (3.28) becomes

Let , then we have to solve the differential equation
, then we have to solve the differential equation . The solution of this differential equation is given for all
. The solution of this differential equation is given for all  by
by

Thus, we get
 (3.30)
(3.30)
We can now obtain the conditional variance swap price by applying Proposition 3.7:

We can also obtain the value of the conditional variance given the full history of .
.
Lemma 3.2 For all , the conditional variance of
, the conditional variance of  is given by
is given by

Proof. By Ito’s lemma we get

Hence, given , we find that
, we find that
 (3.31)
(3.31)
Using (3.27) and the definition of the variance give the result.
Example 3.5 (Heston Model) We continue the study of the Heston model case (see Example 3.4). Thus Equation (3.31) gives

Given (3.30), we know that

which is a function of time  and the Markov process
and the Markov process . Let
. Let , then we have to solve the differential equation given by
, then we have to solve the differential equation given by

The solution of this differential equation is given for all  by
by

where


We finally obtain in the Heston model case that

and that the conditional variance is equal to

4.2. Pricing Volatility Swaps
In this section, we follow the same methodology studied by Broadie and Jain in [8] where there is no regime switching component. We recall that the realized annual stock variance over the life of the contract is given by (3.24) and depends on the values of the Markov process
 . Denote by
. Denote by  the accumulated variance between time 0 to
the accumulated variance between time 0 to . We recall that the process
. We recall that the process  is the solution of the stochastic differential equation given by
is the solution of the stochastic differential equation given by

Hence  is the solution of the stochastic differential equation given by
is the solution of the stochastic differential equation given by . Let define by
. Let define by  the expectation at time
the expectation at time  with respect to
with respect to 
 (3.32)
(3.32)
Hence  depends on the variance process
depends on the variance process
 of the underlying asset and on the Markov process
of the underlying asset and on the Markov process . We call by fair conditional variance strike price the quantity
. We call by fair conditional variance strike price the quantity  which is defined such that Equation 3.25 vanishes:
which is defined such that Equation 3.25 vanishes:

Then, we have that  and for time
and for time
 , we obtain that
, we obtain that . We define now the forward price process
. We define now the forward price process  as
as
 (3.33)
(3.33)
Proposition 3.8 The forward price process  can be expressed as a function
can be expressed as a function  and it is the solution of the system of stochastic differential equations given by
and it is the solution of the system of stochastic differential equations given by
 (3.34)
(3.34)
with boundary condition given by
 .
.
Proof. Rewrite  as
as
 .
.
Applying Itô Lemma to , using (3.26) and the fact that the forward price measure
, using (3.26) and the fact that the forward price measure  is a martingale give the expected result.
is a martingale give the expected result.
5. Conclusions
In this paper, we studied the problem of pricing and hedging options based on an asset which is modeled by a regime switching stochastic volatility model. We presented firstly this class of regime switching stochastic volatility models. We shown that this class of regime switching models encompasses a large panel of classical financial models. We also explained the interest in applications of this kind of models. Secondly, we used the local risk minimization approach to solve the problem of pricing and hedging contingent claims in this incomplete market. Thus, we obtained pricing and hedging formulae and also the formula of the optimal hedging strategy. Finally, we fund formulae to price volatility and variance swap options by solving a system of stochastic differential equations.
Some possible future directions in this field of research are the following:
- Develop a method to estimate all the parameters of this class of regime switching models, including the hidden Markov chain (its transition matrix);
- Apply these pricing and hedging formulae to economic and financial data. Indeed, regarding the existing literature, a good candidate could be the electricity spot price;
- Construct a method to evaluate quickly the solutions of the system of stochastic differential Equations (2.20) and (3.34). A system of spatial and time discretization grids could be considered and investigated.