Optimal Foreign Exchange Risk Hedging: A Mean Variance Portfolio Approach ()
1. Introduction
Beginning in the early 1970s, floating foreign exchange (FX) rates became more common, among the major currencies. Now the recent global financial crisis including euro zone instability have clearly illustrated the critical importance of hedging for risks in foreign exchange rate. See following figures of monthly Euro/Dollar and Yen/ Dollar foreign exchange rates during 1999.1-2011.7, where both FX rates are fluctuating especially after global financial crisis.1
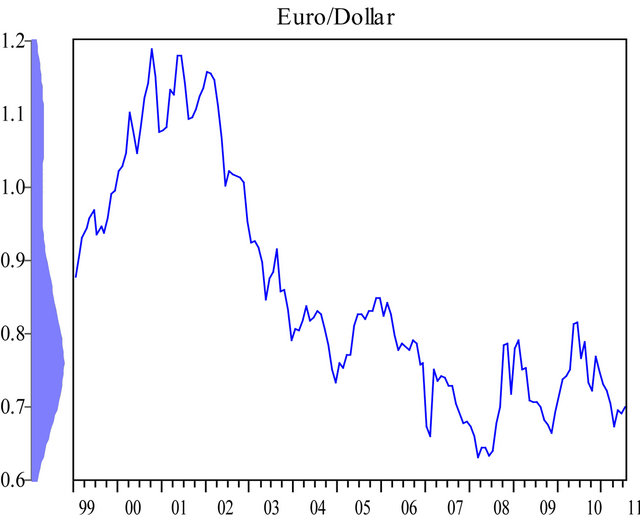

So foreign currency fluctuations are one of the key sources of risk in multinational operations. The various tools which have emerged to deal with foreign exchange risk have been treated extensively in the finance literature. The nature, uses, and efficiency of their markets are quite well understood today (See [1]). The US Department of Commerce is also warning that “The volatile nature of the FX market poses a great risk of sudden and drastic FX rate movements, which may cause significantly damaging financial losses from otherwise profitable export sales (Trade finance guide, http://trade.gov /publications/pdfs/tfg2008ch12.pdf).” The same guide suggests three FX risk management techniques considered suitable for new-to-export US small and mediumsized enterprises companies as non-hedging FX risk management techniques,2 FX forward hedges3 and FX options hedges.4
However, what has been ignored, as correctly pointed out [2], are the factors an investor should consider when choosing from among the various available hedging tools to reduce the risk resulting from a certain type of exposure to foreign exchange risk for a given expected return.
[2] gauges the preferences of finance officers in terms of the specific characteristics of a hedging tool relying on a questionnaire survey. [3,4] illustrate the technique of computerized optimization and simulation modeling to manage foreign exchange risk. However they did not derive the closed form optimal hedging solution analytically and thus it obviously requires the additional computational burden.
So this paper introduces the optimal foreign exchange risk hedging model following a standard portfolio theory. The results indicate that a lower level of risk can be achieved, given a specified level of expected return, from using optimization modeling. In the context of this paper the expected hedging return is defined from the expected cost of the foreign currency using a specified hedging strategy minus the expected cost of the foreign currency when it is purchased form the spot market. The focal point of the technique is its ability to identify optimal combinations of most frequently using hedging vehicles, those are (European) currency options, forward contracts, leaving the position open (foreign exchange risk hedging tools suggested by the US Department of Commerce) in a closed form.5
The rest of this paper proceeds as follows. Section 2 derives the expected return and variance of hedging vehicles. Section 3 analyzes the optimal hedging selection. Section 4 concludes.
2. Moments of Triple Hedging Tools’ Returns
Assume, at time 0, an investor hopes to buy one unit of foreign exchange at a future time . Denotes
. Denotes  as the foreign exchange rate at time
as the foreign exchange rate at time  in terms of domestic currency. For instance,
in terms of domestic currency. For instance, 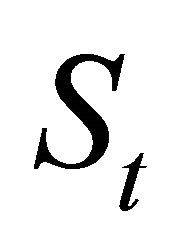 is the dollar price of one euro where the dollar is the domestic currency. Further we suppose that there are three hedging tools, i.e., European currency call option, forward contracts and leaving the position open.6 Define a forward contract rate
is the dollar price of one euro where the dollar is the domestic currency. Further we suppose that there are three hedging tools, i.e., European currency call option, forward contracts and leaving the position open.6 Define a forward contract rate , a striking price
, a striking price  and its premium
and its premium  at time t of European call option with the maturity
at time t of European call option with the maturity , respectively.7
, respectively.7
Now we would like to construct the efficient hedging frontier composed of expected return and variance of each hedging vehicle. So, it is exactly matched with the portfolio possibilities curve. An optimal combination of hedging vehicles is one, which maximizes the expected return given a desired level of risk.
Before proceeding, we assume the logarithm of exchange rate follows a random walk following [5]:
Assumption 2.1. We suppose
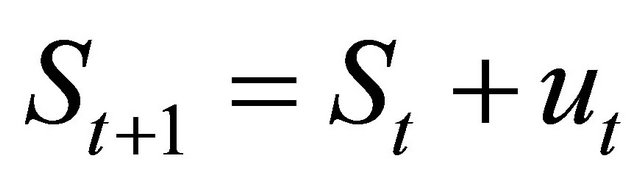
where  and
and  is independent, identically and normally distributed sequence with the mean zero and variance
is independent, identically and normally distributed sequence with the mean zero and variance .
.
Above Assumption 2.1 represents the efficient market hypothesis for the foreign exchange rate. Now we derive the return and its variance of different hedging tools, where the return is computed based upon the purchasing a foreign currency by the spot rate . The expected return is defined from the conditional expectation8 based on the information of past exchange rates
. The expected return is defined from the conditional expectation8 based on the information of past exchange rates  .9
.9
2.1. Derivation of Mean and Variance
At first, we derive the expected return [Rn] and its variance [Vn] of non-hedging (leaving the position open) as:
Proposition 2.2. Suppose Assumption 2.1 holds. Then the expected return for non-hedging is  and its variance is
and its variance is .
.
Proof. Note the return of non-hedging is the negative10 value of following:11
 (1)
(1)
assuming 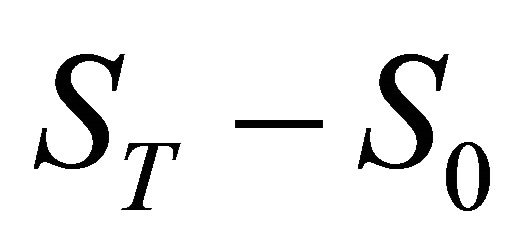 is small. Then, under Assumption 2.1, the claimed results hold as:
is small. Then, under Assumption 2.1, the claimed results hold as:
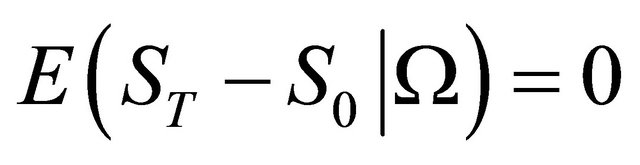
and
 .
.
At second, we derive the expected return  and its variance
and its variance  of forward contract as:
of forward contract as:
Proposition 2.3. Suppose Assumption 2.1 holds. Then the expected return of forward is  and its variance is
and its variance is  where
where .
.
Proof: Note the expected return for forward is the negative value of following:

assuming 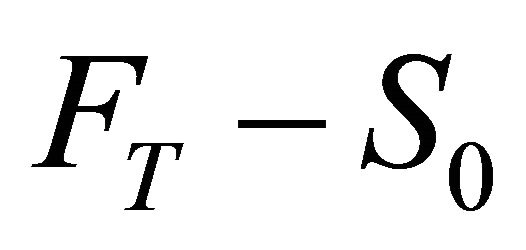 is small. Its variance is obviously zero since the return is not random.
is small. Its variance is obviously zero since the return is not random.
Above forward contract may dominate the non-hedging if its expected return is positive, which is riskless. Such dominance may be closely related with the interest rates whenever the covered interest parity holds. See following result.
Corollary 2.4. Suppose Assumption 2.1 holds and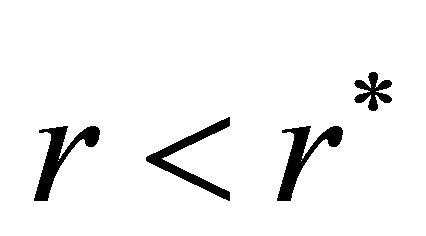 . Then the forward contracts dominates the nonhedging where
. Then the forward contracts dominates the nonhedging where  and
and 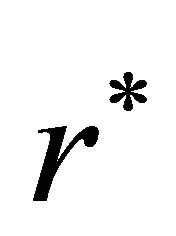 denote the domestic and foreign risk free interest rates respectively.
denote the domestic and foreign risk free interest rates respectively.
Proof. From the covered interest parity, note  =
= . So if
. So if  or
or , then there is positive expected return without risk. In this case, the forward contract dominates the non-hedging case.
, then there is positive expected return without risk. In this case, the forward contract dominates the non-hedging case.
Above result also implies that if the domestic interest rate is higher than the foreign interest rate, then the non-hedging may better than the forward contract.12
Now we derive the expected return [R0] and its variance [V0] of currency call option as:
Proposition 2.5. Suppose Assumption 2.1 holds. Then 1) the expected return of currency call option is given as:

and 2) its variance is
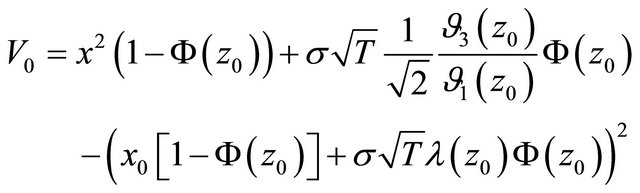
where ,
,  ,
,  ,
, 
and  where
where  and
and  are the standard normal density and distribution function respectively and
are the standard normal density and distribution function respectively and  denotes the distribution function of
denotes the distribution function of  distribution with the degree of freedom
distribution with the degree of freedom .
.
Proof. 1) Note the outflow of call option at time  is given as
is given as  where
where  is the option premium. Thus its return is the negative value of following:
is the option premium. Thus its return is the negative value of following:

assuming  and
and  are small.
are small.
Now the expected return conditional on  is the negative value of following:
is the negative value of following:

where , since
, since
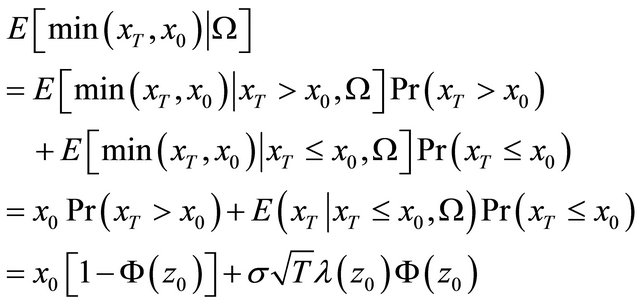 (2)
(2)
from the definition of conditional expectation, where  from Assumption 2.1 and
from Assumption 2.1 and
 (3)
(3)
for the Equality (2) from [7] (p. 759), and
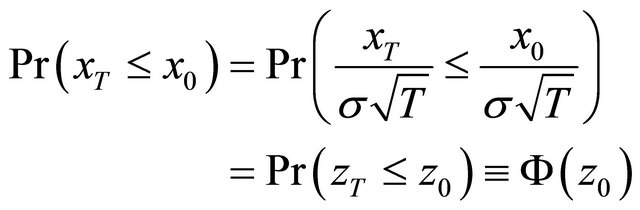
where .
.
2) The return’s variance of call option conditional on  is defined as:
is defined as:
 (4)
(4)
Note the second term of (4) is derived from (2) directly. Then the first term of (4) is arranged as:
 (5)
(5)
from the definition of conditional expectation for the first equality.
However we may show
 (6)
(6)
from following facts (b-i) and (b-ii):
 (b-i)
(b-i)
since 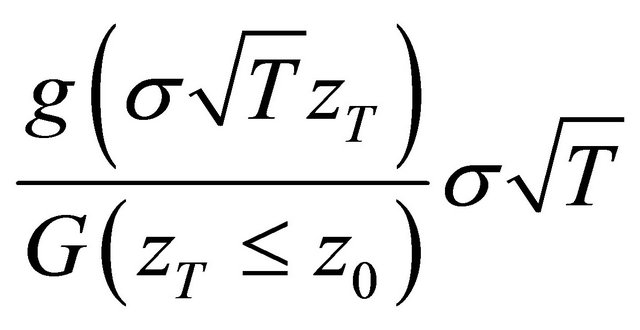 is the truncated density function of variable
is the truncated density function of variable 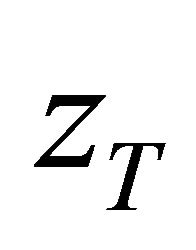 since
since

from the change of variable formula where  and
and  denote the density and distribution functions of
denote the density and distribution functions of  respectively, and
respectively, and  since
since  by definition.
by definition.
 (b-ii)
(b-ii)
from [8] (Remark 3), where
 and
and where
where

and
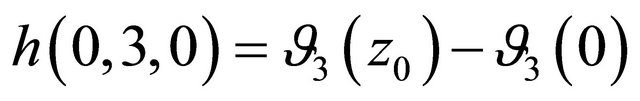
in [8] (Remark 3) where .
.
Finally if we plug (6) into (5), then we get the claimed result as:

2.2. Derivation of Covariances
At second, we derive the covariance among three hedging tools. Note the covariance of returns between nonhedging (or option) and forward is obviously zero since the forward return is not random. Then the covariance of returns between option and non-hedging is given as:
Proposition 2.7. Suppose Assumption 2.1 holds. Then the covariance of returns between option and non-hedging is
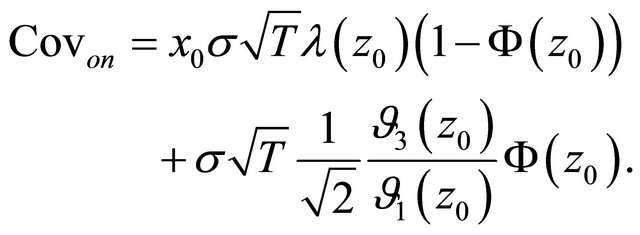
Proof. Note the covariance between non-hedging and option conditional on  is defined as:
is defined as:

since the fourth equality holds from 
Now the claimed result is derived since

from (3) and (6) for the last equation and
 .
.
3. Efficient Hedging Frontier Construction
Based upon above derivation of return structure, now we may derive the efficient hedging frontier. It is exactly matched with the portfolio possibilities curve in a standard portfolio theory (see [9] for a nice introduction).
For this purpose, first of all, we consider a portfolio composed of non-hedging and call option that are all risky. Let the weight of non-hedging be as w and 1 − w for the option where w is a number. Then, from the above derivation, its expected return is defined as:

and its variance is given as:

where 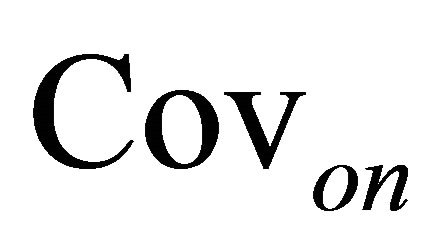 denotes a covariance between the returns of non-hedging and call option.
denotes a covariance between the returns of non-hedging and call option.
In our case, the return of forward has the zero variance with the expected return is . Thus it is regarded as the riskless asset in the standard portfolio theory. Now the hedging allocation line13 connecting the riskless forward contract and a combination of non-hedging and call option is defined as:
. Thus it is regarded as the riskless asset in the standard portfolio theory. Now the hedging allocation line13 connecting the riskless forward contract and a combination of non-hedging and call option is defined as:
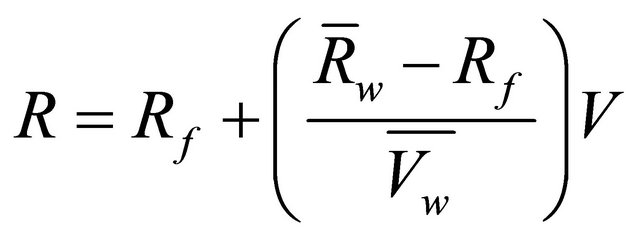 (7)
(7)
where 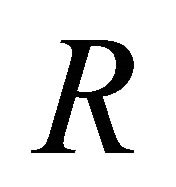 denotes the return and
denotes the return and  denotes the risk;
denotes the risk;
 is a slope.
is a slope.
Then the efficient hedging allocation line14 is given by solving following problem:
 (8)
(8)
that is maximizing the slope of Equation (7) with the argument w.
The problem (8) may be solved without restriction by [9] (pp. 100-103) as:
 (9)
(9)
where
 .
.
If  or
or , then the maximization problem (8) should be solved under the restriction
, then the maximization problem (8) should be solved under the restriction  using a typical Kuhn-Tucker condition.
using a typical Kuhn-Tucker condition.
Finally, the efficient hedging frontier is given by
 (10)
(10)
where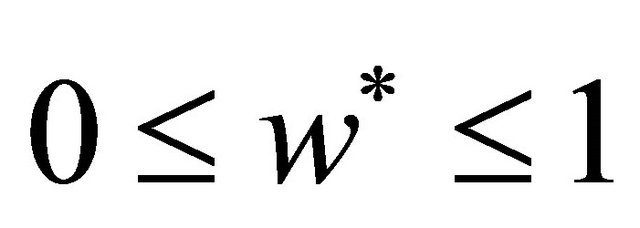 .
.
For the given efficient frontier in (10), optimal hedging (c.f., separation theorem) is conducted as follows. At first, the hedging ratio between non-hedging and option re set as . At second,
. At second,  is set for the forward and
is set for the forward and  is set for the first combination of non-hedging and option. Expected utility maximization may be a rule to determine a
is set for the first combination of non-hedging and option. Expected utility maximization may be a rule to determine a . Finally
. Finally
 becomes the optimal hedging ratio of the forward, non-hedging and call option. See following Figure 1.
becomes the optimal hedging ratio of the forward, non-hedging and call option. See following Figure 1.
Now we suggest an example that shows how above result may be applied in the field.
Example 3.1. Above result is applied to the dollar as domestic currency and the yen as the foreign currency. To compute the efficient hedging frontier in (10), we let  months,
months,  (August 18, 2010),
(August 18, 2010),
 ,
,  ,
,  dollar/100yen and an estimator of
dollar/100yen and an estimator of  (during 2005.1- 2009.12).
(during 2005.1- 2009.12).
Then, at first, we get ,
,  ,
,  ,
,  ,
,  and
and  from the above results. Then we obtain the return
from the above results. Then we obtain the return 
and variance  of the portfolio non-hedging and option where
of the portfolio non-hedging and option where .
.
From this result, the Equation (10) in the efficient hedging frontier becomes:
 (11)
(11)
Suppose an extremely risk-averse investor maximizes
a utility function  subject to (11).15 The resultant portfolio induces
subject to (11).15 The resultant portfolio induces  and
and . It implies
. It implies  where the utility is maximized with the constraint (11). Thus the forward, non-hedging and option are finally selected as
where the utility is maximized with the constraint (11). Thus the forward, non-hedging and option are finally selected as

4. Conclusion
We introduced the optimal foreign exchange risk hedging model following a standard portfolio theory. The results indicate that a lower level of risk can be achieved, given a specified level of expected return, from using optimization modeling. The structure may be extended to cover the futures and American options and we will take it as a future research topic. However I am sure the similar logic may be readily applied to these extensions. Further a development of convenient computer program for FX risk hedging users based on above results might be a useful project.
NOTES
2The exporter can avoid FX exposure by using the simplest non-edging technique: price the sale in a foreign currency. The exporter can then demand cash in advance, and the current spot market rate will deterne the US dollar value of the foreign proceeds.
3The most direct method of hedging FX risk is a forward contract, which enables the exporter to sell a set amount of foreign currency at a pre-agreed exchange rate with a delivery date from three days to one year into the future.
4Under an FX option, the exporter or the option holder acquires the right, but not the obligation, to deliver an agreed amount of foreign currency to the lender in exchange for dollars at a specified rate on or before the expiration date of the option. As opposed to a forward contract, an FX option has an explicit fee, which is similar to a premium paid for an insurance policy.
5At least author’s knowledge, there are not any the same researches in this direction.
6It is a non-hedging and to buy the foreign currency at time .
.
7The value of call option was derived by [6].
8Note the conditional expectation is the optimal forecasting of return which minimizes the mean squared forecasting error.
9So an investor exploits the information  when she determines the optimal hedging tool.
when she determines the optimal hedging tool.
10It is negative because buying of foreign currency means the outflow of domestic currency.
11We do not consider the cost-of-carry for the spot purchasing of foreign currency since it is applied for the other hedging vehicles by the same amount. In particular, suppose an interest  is required to borrow the
is required to borrow the  till time
till time  and then the non-hedging return Formula (1) may be revised as;
and then the non-hedging return Formula (1) may be revised as;

Thus it does not matter even if we just focus on the  since the other terms
since the other terms  and
and  are same for the other hedging tools.
are same for the other hedging tools.
12This result well explain why a lot of firms of the developing countries with the high interest rate do not use the forward contract. The problem is the cost to use the forward is bigger than the non-hedging if 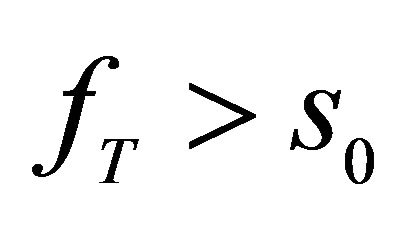 even though there is the risk difference.
even though there is the risk difference.
13It is called as the capital allocation line in the portfolio theory.
14It is called as the capital market line in the portfolio theory.
15This utility function largely penalizes the risk and reflects deep risk aversions (e.g., under recent financial crisis). Of course other utility functions may be readily applied.