Type-2 Fuzzy Logic Controllers Based Genetic Algorithm for the Position Control of DC Motor ()
1. Introduction
Fuzzy logic controllers (FLCs) are usually constructed using type-1 fuzzy sets [1], referred to as type-1 FLCs. Such FLCs have been applied to many areas, especially for the control of complex nonlinear systems that are difficult to model analytically [2,3]. Despite their popularity, research has shown that type-1 FLCs may have difficulties in modeling and minimizing the effect of uncertainties [4]. This limitation may restrict the usefulness of design methods that tune the FLCs using the genetic algorithm (GA) and a model of the controlled process. Since it is impossible for a model to capture all the characteristics of the actual plant, the performance of a controller designed using a model will inevitably deteriorate when it is applied to the practical system. A controller takes fully into account the non-linear ties. Emerging intelligent techniques have been developed and extensively used to improve or to replace conventional control technique because these techniques do not require a precise model. One of intelligent technique, fuzzy logic by Zadeh is applied for controller design in many applications. The advantage of fuzzy control methods [5] is the fact that they are not sensitive to the accuracy of the dynamical model. With the development of T2 FLSs and their ability to handle uncertainty, utilizing type-2 FLCs (IT2 FLCs) has attracted a lot of interest in recent years. The concept of type-2 fuzzy sets was first introduced by Zadeh as an extension of the concept of well-known ordinary fuzzy sets, type-1 fuzzy sets. A type-2 fuzzy set [6] is characterized by a fuzzy membership function i.e. the membership grade for each element is also a fuzzy set in [0, 1], unlike a type-1 fuzzy set, where the membership grade is a crisp number in [0, 1]. The membership functions of type-2 fuzzy sets are three dimensional and include a footprint of Uncertainty (FOU), which is the new third dimension of type-2 fuzzy sets. The footprint of uncertainty provides an additional degree of freedom to handle uncertainties. In this paper, the application of type-2 fuzzy logic concepts to the position control of a simple dc motor is illustrated. The device model is straightforward and the physical implications of position control are readily perceived.
2. Genetic Algorithm (GA)
GA was first proposed in 1975 [7]. GAs are theoretically provide a robust search in complex spaces [8]. Figure 1 contains the flow chart of a basic GA. First, a chromosome population is randomly generated. The fitness of all individuals with respect to the optimization task is then evaluated by a scalar objective function (fitness function).
Genetic operators such as crossover and mutation are applied to the parents in order to produce a new generation of candidate solutions. As a result of this evolutionary cycle of selection, crossover and mutation, more and more suitable solutions to the optimization problem emerge within the population. Increasingly, GA is used to facilitate FLSs design [9]. However, most of the works discuss type-1 FLC design. This paper focuses on genetic algorithm of type-2 FLCs. There are two very different approaches for selecting the parameters of a type-2 FLS [4]. Type-2 FLCs designed via the partially dependent approach are able to outperform the corresponding type-1 FLCs [9], The type-2 FLC has a larger number of degrees of freedom because the fuzzy set is more complex. The additional mathematical dimension provided by the type-2 fuzzy set enables a type-2 FLS to produce more complex input-output map without the need to increase the resolution. To address this issue, a comparative study involving type-2 and type-1 FLCs with similar number of degrees of freedom is performed. The totally independent approach is adopted so that the type-2 FLC evolved using GA has maximum design flexibility.
3. Interval Type-2
The structure of a type-2 FLS is shown in Figure 2. It is similar to its type-1 counterpart, the major difference being that at least one of the fuzzy sets in the rule base is type-2. Hence, the output of the inference engine is type- 2 sets and a type-reducer is needed to convert them into type-1 sets before defuzzification can be carried out.
3.1. Inference
An interval type-2 FLS is employed [4]. “Interval” means that the input/output domains are characterized by interval type-2 sets [5], whereby the membership grades
of all elements in the FOU (secondary membership grades) area nifty. The inference engine then matches the fuzzy rules in the rule base. To compute unions and intersections of type-2 sets, compositions of type-2 relations are needed. Just as the sup-star composition is the backbone computation for a type-1 FLC, the extended sup-star composition is the backbone for a type-2 FLC [4].
3.2. Type-Reduction and Defuzzification
The output of the inference engine is a type-2 fuzzy et, it must be type-reduced before the defuzzifier can be used to generate a crisp output. This is the main structural difference between type-1 and type-2 FLCs. The most commonly used type-reduction method is the center-of-sets type-reducer, which may be expressed as [4].
The footprint of uncertainty (FOU) of the membership function (MSF) in the IT2FLS is the area which limited by two MSF, the overhead limitation is the upper membership function UMSF and the down limitation is the lower membership function (LMSF), as shown in Figure 3.
4. DC Motor Model
In this study, proposed approach has simulated a DC shunt motor as is shown in Figure 4. The characteristics equations of the DC motor can be defined by the following equations [10];
 (1)
(1)
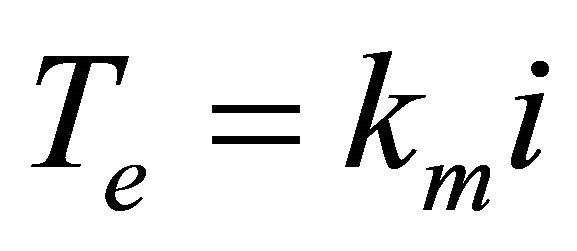
 (2)
(2)
 (3)
(3)
 (4)
(4)
The transfer functions are defined for speed and position control of DC motor, respectively.
 (5)
(5)
where Ra is armature resistance, La is armature inductance i is armature current, V is armature voltage, ea is back emf voltage, Ke is back emf constant, Km is torque constant, Tm is torque developed by the motor, ω is angular speed of shaft, θ is angular displacement of shaft, J is moment of inertia of motor and load, B is frictional constant of the motor and load. Unlike conventional control, which is based on mathematical model of a plant, a FLC usually embeds the intuition and experience of a human operator and sometimes those of designers and researchers. While controlling a plant, a skilled human operator manipulates the process input (i.e. controller output) based on with a view of minimizing the error within shortest possible time. The controlled variable of fuzzy controller is u(t). Once the fuzzy controller inputs and outputs are chosen, one must think about the membership functions (MSFs) for these input and output variables. In this paper, all membership functions for the conventional fuzzy controller inputs (e and Δe) and the controller output are defined on the common normalized domain [−1, 1]. We use symmetric triangles (except the two MFs at the extreme ends) with equal base and overlap with neighboring MFs. This is the most natural and unbiased choice for MFs. The actual control input voltage for the main fuzzy controller (In the case of PI-type FLC) can be written as
 (6)
(6)
where k is the sampling instant, is the crisp at k sampling instant and is the incremental change in controller output. showed that an IT2 fuzzy-PI (or the corresponding PD) controller is equivalent to a nonlinear PI (or PD) controller with variable gains and control offset [11].
5. Simulation
In this section. The assumed parameters of the electric DC motor represented in the following transfer function.
 (7)
(7)
5.1. Experiment Analysis of Fuzzy Type-1 & Fuzzy Type-2 without GA
Simulation experiments under different operation status is carried out based on the fore established model and performance comparison with IT2FLC and conventional type-1 fuzzy controller is made. The two curves in Figure 5 are the simulation curves of the rated running state for DC motor respectively under the control of conventional type-1fuzzy controller and the type-2 fuzzy controller. For a clear comparison between the conventional fuzzy controller and the clustering based fuzzy controller, several performance measures such as peak overshoot (%OS), settling time, rise time, integral absolute error (IAE) and integral-of-time-multiplied-absolute error (ITAE) are computed as shown in Table 1. Using fuzzy type-1 and type-2 controller, the rise time and settling time not good whereas for other measures, both the controllers give approximately the same performance.
5.2. Fuzzy Type-1 & Fuzzy Type-2 with GA
In this section, DC motor is used in simulation. The genetic algorithm is very useful in optimization technique.

Figure 5. Response of T1FLC & T2FLC OF DC motor.
Table 1. Numerical result of experiment on DC motor without disturbance.

it is apply in this paper of fuzzy type two logic controller in multi position of simulation process, to measured the optimal parameters of fuzzy such as scaling factor input and output data, start-end point of triangular memberships function (bottom triangle) and center of memberships function (top triangle). The number of variable parameters are thirty two parameters. Figure 6 compares the simulation results of the two controllers when the external disturbance is zero. The performance of the two controllers is listed in Table 2. Observe that GA type-1 FLC has a noticeable overshoot and a slower convergence to the set point in comparison to GAIT2FLC. Clearly, the GAIT2FLC has zero overshoot. It is easy to see that GAIT2 FLC has a faster settling time than GA type-1 FLC. However, under disturbance, the performance of the scheme shows improved results. Figure 7 shows the zoom of response of the system with a 30% disturbance applied at t = 0.36 sec. Table 3 shows the values of peak overshoot, settling time, IAE and ITAE computed under this condition. At the time t = 0.36 sec, the external torque is decreased by a step of 25% Figure 8. The system again reaches the steady state after transient period. Table 4 shows the values of peak overshoot, settling time, IAE and ITAE computed under this condition. The illustrated figures verify that a significant improvement has been achieved using the proposed genetic algorithm (GA) type-2 fuzzy controller.
Initially the motor is operated at the steady state. At the time t = 0.36 sec, an increased step of 25% of initial

Figure 6. Response of T1FLC & T2FLC OF DC motor without disturbance.
Table 2. Numerical result of genetic simulation on DC motor disturbance.


Figure 7. Response of GAT1FLC & GAT2FLC on DC motor with disturbance.
Table 3. Numerical result of simulation on DC motor with disturbance.


Figure 8. Response of GAT1FLC & GAT2 on DC motor sudden decrease in position.
Table 4. Numerical result of simulation on DC motor with sudden decrease in position.
set point. As shown in Figure 9 the motor position tracks the new set point after a transient period. Obviously, the external torque is assumed constant. Table 5 shows the values of IATE and IAE under these conditions. Comparisons with the conventional fuzzy controller indicate the improvement achieved.
5.3. Fuzzy Type-1 & Fuzzy Type-2 with Random Noise GA
In this section, we show in Figure 10 the simulation results for control of DC motor using both the GA type-2 fuzzy controller and the conventional fuzzy controller when used random noise reference signal.

Figure 9. Responce of GAT1FLC & GAT2FLC on DC motor sudden increased in position.
Table 5. Numerical result of simulation on DC motor with sudden increased in position.

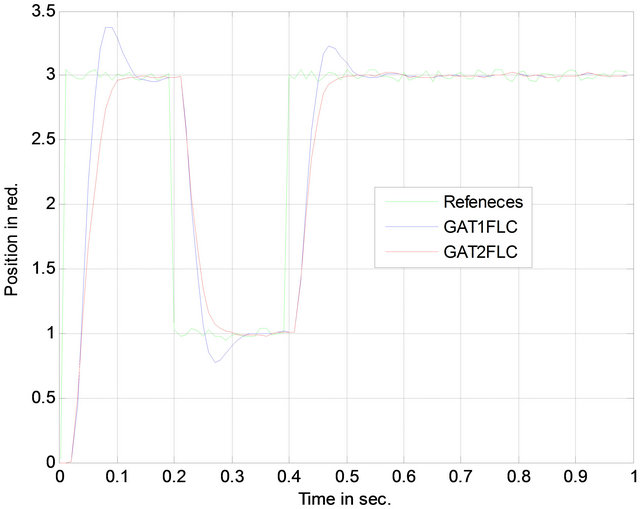
Figure 10. Response of GAT1FLC & GAT2FLC on DC motor with random noise.
6. Conclusions
In this paper, The GAFLCT2 has been proposed for position control of DC motor. Performance of the proposed GAFLST2 was also compared with corresponding conventional GAFLCs with respect to several indices such as rise time, settling time, maximum peak overshoot (MP%), integral of absolute error (IAE). and integral time of absolute error (ITAE).
The simulated results show that, using a type-2 FLC in real world applications can be a good option since this type of system is a more suitable system to manage high levels of uncertainty, as we can see in the results shown in Tables 2-5. Simulation results indicate that the performance of the GA FLCT2 will better. That is mean the system will sense for change the value of IAE and ITAE. The results demonstrate that a type-2 FLC can outperform type-1 FLCs that have more robustness design parameters. The main advantage of the type-2 FLC appears to be its ability to eliminate persistent oscillations, especially when unmodelled dynamics were introduced. This ability to handle modeling error is particularly useful when FLCs are tuned offline using GA and a model as the impact of unmodelled dynamics is reduced. The significance of the work is focused to manage the uncertainty of the system. The nonlinear of the systems are big problem therefore the one of successful methods to eliminate or reduce nonlinearity system by using fuzzy type two. It is a good option for real time applications that limited time is needed such as robot system.