The Dynamic-to-Static Conversion of Dynamic Fault Trees Using Stochastic Dependency Graphs and Stochastic Activity Networks ()
1. Introduction
Nowadays, technology and technological systems are fundamental constituents of any industrial process. In such a context, the demand of more effective and precise risk assessments and performability evaluations has highlighted the necessity of adequate, specific dependability evaluation techniques and methods. In fact, such dependability techniques and methods have to be able to effectively capture the behavior of modern systems, subsystems and components which could be characterized by interdependencies and interactions. Many methodologies have been formulated to achieve these objectives and implement efficient solution techniques. Among these, Dynamic Fault Tree (DFT) [1,2] stands out for its characteristics including: a valid formalism, a high level language of description and several resolution algorithms. For these reasons DFT has became a benchmark for many other modeling framework for the dependability.
Many efforts have been made to address the following main issues: 1) the problem of the state space explosion of the equivalent Continuous Time Markov Chain (CTMC) [3-7]; and 2) the need of a more generalized formalism to tackle various kind of complex systems and able to perform different dependability studies [8-18]. In [12] a powerful framework able to tackle general dependencies is presented. However, dependencies can be implemented only through connections (i.e., denoted as triggers) between the elements of the Fault Tree. In this way, complex relationships can be added abusing of the Fault Tree notation, which can, in the end, results in an explosion of the tree.
The main motivation of this work is to expand the modeling power capabilities of dependability tools, such as DFTs, and maintain a high level formalism of description. The issues addressed in this paper concern: 1) the lack of the general modeling techniques to include stochastic dependencies between events not directly related by a fault (i.e., a more general approach to model statedependent components behavior); and 2) the handling of general sojourn time distributions, non-Markovian processes (e.g. time delays), inhibitions, multiple failure modes, etc.
To achieve these objectives a modeling framework based on a modular approach is presented. The methodology makes use of two high level models that decouple stochastic dependencies and the system fault logic through:
a stochastic Dependency Graph (DG) and a generic fault schema. Hence, dependability measures are evaluated through the combination of the information provided by these two models.
The framework results incredibly flexible because the DG and the fault schema are independent. The former embeds the dependencies among the components, the latter embeds the system fault logic. Moreover, this last one can be constructed in several ways (i.e. FT, RBD, Event Tree, etc.). In this way, it is possible to generate a behavioral model on the basis of the information contained in the DG and compute many Reward Functions (RF; like the reliability, availability, reliability with repair, conditional probabilities, etc.) attaching the information derived from the system fault schema.
In this paper is presented an application of this modeling framework and a practical case study to convert DFT will be shown: the stochastic dependencies of the DFT will be captured by the DG model, while the system fault logic will be described by a static Fault Tree (FT). In the following this modular model is referred as a Stochastic Dependency Graph Fault Tree (DGFT).
The objectives of this methodology can be listed as follow:
• Create a more flexible approach for the dependability modeling in presence of state-dependent components behavior;
• Model new dependencies logics that are not expressed through the dynamic gates of the DFT;
• Assess various dependability studies using one single model;
• Evaluate dependability measures of complex systems by the mean of analytical and simulating methods easily retrievable from the high level models.
The remainder of the paper is structured as follow: in Section 2 a general description of DGs’ basic elements is given and a general mathematical expression stating the state-dependent transition rate of components with exponential behavior is given; in Section 3 is presented the general procedure to convert DFTs in DGFTs and the subsequent lower level conversion that is needed to calculate the RF; Section 4 is concerned with the derivation of the intermediate level models; in Section 5 a case study (taken from the literature) [10] is solved to show the DFT to DGFT conversion and the resolution procedure; Section 6 reports conclusion and future works.
2. Stochastic Dependency Graphs
A DG is a model that highlights stochastic dependencies between components. The elements of a DG are nodes, direct links and dependency gates. Each component is represented by a node and nodes are linked together by the mean of direct links and dependency gates. Connections represent stochastic relationships among components. Components not affected by stochastic dependencies are drawn as isolated nodes while components subjected to dependencies will be drawn as nodes intercomnected by direct links and gates.
It is worth to distinguish between parents and child components. Parents components are components whose the entering in a particular state force some change in the parameter of the sojourn time distribution (or more generally the entire distribution law) of the child component. A node can be both a parent and a child for some other node.
Among all the kind of dependencies some basic dependency types are reported in this paper: elementary, AND, OR and k/N:
• An elementary dependency exist between a parent and a child component if a change in the state of the parent forces a change in the child sojourn time distribution;
• In an AND dependency gate the child is affected from its parents if all them are in a specific state;
• In an OR dependency gate the child is affected if at least one of its parents is in a specific state;
• In a k/N dependency gate the change is dictated from all the combinations of the N parents where k of them are in a specific state. It generalizes the AND and OR dependency gates in the case that k is respectively equal to N and one. In the case that both k and N are equal to one the dependency gate is further reduced to an elementary dependency link.
Generally the specific state is represented by the failed state. Figure 1 shows the graphical representation of the four kinds of dependencies introduced above.
For a DG constituted by any combination of the basic elements above introduced, qualitative MCS (or DMCS in case of dynamic dependencies) can be derived. They can be used to specify the reactivation conditions in thebehavioral model (see Section 4).

Figure 1. DG elements: (a) Elementary dependency link; (b) AND dependency gate; (c) OR dependency gate; (d) k/N dependency gate. Pi: parent node; C: child node.
In the following a mathematical expression to calculate the system-state-dependent failure rate of a component under a k/N dependency gate is shown. The results refer only to exponential sojourn time distribution but they can be further generalized.
Let us consider a system with two state components (i.e. “working-failed” or “UP-DOWN”). Let us denote with si the state of the generic i-th component: si can assume two values, one or zero standing respectively for working and failed. Let us define the set I as the set of all input component indexes. Let say h as the generic element of I. Thus, .
.
Let call CiI as the set of all the subset of I of cardinality i, with . The cardinality of the generic set CiI is defined as #CiI. Let us denote each subsets of CiI with CiI(j), with
. The cardinality of the generic set CiI is defined as #CiI. Let us denote each subsets of CiI with CiI(j), with , #CiI. In this way each subset CiI(j) represents a collection of input indexes. The current failure rate (i.e., dependent on the current parents state configuration) of the child component is given by:
, #CiI. In this way each subset CiI(j) represents a collection of input indexes. The current failure rate (i.e., dependent on the current parents state configuration) of the child component is given by:
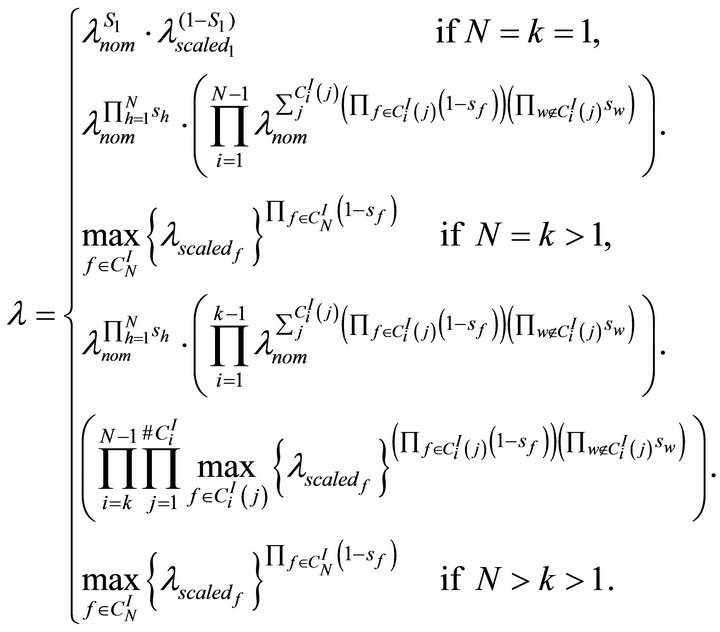 (1)
(1)
where λnom and  are the failure rate of the child component when: no dependency effects are present (nominal) and when subjected to the dependency effects of the parent f (scaled).
are the failure rate of the child component when: no dependency effects are present (nominal) and when subjected to the dependency effects of the parent f (scaled).
It is necessary to specify that when λnom is equal to zero (e.g. SPARE in cold stand-by or SEQ) the formula 00 is equal to one and that when  is equal to infinite (e.g. FDEP gate) the formula ∞0 is also equal to one (this is not mathematically correct but allows a compact representation of the expression above).
is equal to infinite (e.g. FDEP gate) the formula ∞0 is also equal to one (this is not mathematically correct but allows a compact representation of the expression above).
Equation (1) is the most general form to assess the current failure rate of a child component given the state of its parents. It is suitable for each of the dependency gate discussed above.
Equation (1) is enough general to model systems where the failure rate of the child component assumes different values depending on the kind of failed parent (e.g. a repeated component in a SPARE and a FDEP gate). In this case the impact on the failure rate of the child can be different depending on which parent forces the dependency logic. The operator max is used to address situations where the predominant effect must be chosen.
To model some other relationship between parents and child (e.g. modeling joint effects does not require the max operator) other gates can be introduced, thus generalizing the model for any circumstance.
If a DG is composed of a cascade of gates, Equation (1) must be evaluated in a bottom-up procedure. To this end, the possible states of the gates need to be estimated as well as the transition rates determined from these states (Table 1).
3. DFT-DGFT Conversion
In this section the general approach to convert a DFT in a DGFT model is described. The procedure is carried in three steps (Figure 2): the construction of the FT and the DG model (i.e., the high level models); the construction of the behavioral model and the calculation of the MCS (i.e., the medium level models); and the estimation of the RFs.
In the first step the stochastic dependencies included in the logic of SPARE, FDEP and SEQ gates are designed through the DG model. In this way, all the dynamic gates can be replaced by the appropriate static gates (i.e., preserving the fault logic). This is not the case of the PAND gate since no stochastic dependencies are introduced by this gate (i.e., it describes a kind of fault time dependency). A procedure to solve models including this gate is reported in Section 4.
The second step consists in the construction of the medium level models. A model representing the behavior of the system can be constructed on the basis of the DG model. For instance it can be expressed by Generalized Stochastic Petri Nets (GSPN) [14,15,19]. GSPNs are a powerful tool due to the possibility to conduct simulations and convert them in CTMCs. Also more general

Table 1. DG reduction: Ai component name; SAi component state; SAi = 1 “UP; SAi “DOWN”; λi failure rate of child component if parent i is failed.

Figure 2. DFT-DGFT conversion framework.
Discrete Event Simulation (DES) [16-21] models can be used and, in this case, the DG provides a dependency matrix and mathematical expressions (such as (1)) used to update the system-state-dependent distribution law of the system components.
The medium level of the fault model is then extracted in order to evaluate the set of states of the system that concur to the calculation of the RF. This operation is trivial since the FT, obtained at the previous stage, is free of complex formalisms and can be solved via the Minimal Cut Set (MCS) [22]. In some case instead of calculating the MCS, it can be convenient to create the GSPN model of the FT and link it to the GSPN behavioral model. Models concerning with general type of RFs and with fault time dependencies (e.g. PAND gates) can require the construction of this other medium level model.
The RF is finally calculated by joining the two medium level models. The solution can be achieved via the conversion of the GSPN model to a CTMC or obtained via simulation.
Generally, analytical solutions are preferred, but in cases where 1) the state space is too big; 2) the dynamic behavior of the system is too complex; 3) general sojourn time distributions are used, a solution based on simulation can be obtained with precision dependent on the simulating time (i.e., number of batches).
Figure 2 represents schematically the DFT conversion and the resolution process of a DGFT. If the DGFT is used as a stand-alone methodology the procedure starts from the second level of the process depicted in Figure 2. In the case the fault schema used is not a FT, no differences are encountered in the resolution of the model. In fact the MCS represent just that set of condition of interest from a dependability point of view and can be evaluated through any other fault schema.