Optimization of Critical Systems for Robustness in a Multistate World ()
1. Introduction
Broadly speaking, critical systems are systems necessary for mission success and whose failure poses a significant danger to life and property. They are typically complex systems required to perform reliably over a wide range of scenarios. For example, critical infrastructures are characterized as follows [1, p. 30]:
“Our critical infrastructures are particularly important because of the functions or services they provide to our country. Our critical infrastructures are also particularly important because they are complex systems: the effects of a terrorist attack can spread far beyond the direct target, and reverberate long after the immediate damage.”
Seldom does a homogeneous system exist that performs best for all scenarios of interest. The focus of the paper is on choosing the “preferred” solution given a set of alternatives for scenarios with probabilities and consequences that have been assessed either objectively or subjectively. Following the risk-uncertainty classification of Luce and Raiffa [2], this is a problem of “decision making under risk”.
Von Neumann and Morgenstern (vNM) [3] proved that the maximization of expected utility principle proposed by Daniel Bernoulli 200 years earlier is derivable from a set of axioms that appear to be reasonable. Savage [4] developed an axiomatic subjective expected utility theory with a focus on general decision problems rather than simply monetary lotteries. These seminal works resulted in the wide acceptance of what is referred to as Expected Utility Theory (EUT). The EUT is a normative theory that prescribes how the “Rational Individual”1 should make decisions under risk for any type of outcome2, money being a special case. But there is now a large body of evidence, mostly based on testing in the context of lotteries with monetary prizes, that the “rational individual”3 often systematically violate the EUT axioms. These deviations have been labeled “paradoxes”. There are two plausible explanations for them: 1) they are caused by errors of reasoning, or 2) the EUT axioms, like all theories and models, have limitations as descriptive models of rational human behavior because the rational individual follows a different type of reasoning than the Rational Individual. The evidence and strength of the arguments are mounting in favor of the latter explanation. Fishburn [5, p. 86] writes:
“There are certain patterns of preference held by reasonable people for good reasons that simply do not agree with the axioms of expected utility theory and which suggest the need for serious reappraisal of the normative foundations of decision making under risk.”
In recent years, several alternative theories of decision making under risk have been proposed to explain behavioral departures from EUT. The original prospect theory [6] and the newer cumulative prospect theory [7] have become the prominent descriptive theories of decision making under risk. They focus on biases in the human perception of probabilities and outcomes. Regret Theory (RT) [8-9] incorporates the concepts of regret and its counterpart, rejoicing, by adding a contribution to the EUT that accounts for these psychological influences. Disappointment Theory (DT) [10-11] models disappointment and its counterpart, elation, as complementary to both EUT and RT. There has also been much work to develop Generalized Expected Utility Theories (GEUT) by modifying the EUT axioms to account for preference patterns of rational individuals [12] and their perception catastrophic risks [13].
From the perspective of complex systems and Analysis of Alternatives (AoA), a key limitation of EUT is that it is a compensatory model. The poor performance of a system or bad outcome of a decision for one scenario can be mathematically compensated for by the other scenarios. Consequently, an alternative with the Maximum Expected Utility (MEU) may possess vulnerabilities for some scenarios that competitors in the commercial world and adversaries in the military world could exploit [14]. Depending on the context, a DM may prefer a robust solution, one that performs relatively well over a wide range of scenarios. The preferred choice for success and reduced risk often depends on FARness (Flexibility, Adaptiveness, and Robustness) rather than MEU [15]. Given its use of averages as decision criteria, EUT is susceptible to the “Flaw of Averages” [16] including insensitivity to low-probability catastrophic events. This limits its usefulness as a normative model for choosing critical systems [17].
Markowitz [18, p. 207] makes an interesting and convincing argument against maximizing the expected return from the field of investment portfolio theory:
“An investor who sought only to maximize the expected return would never prefer a diversified portfolio. If one security had greater return than any other, the investor would place all of his funds in this security.”
The above argument readily generalizes to the selection of critical systems. Given a set of alternatives, the best strategy for FARness in a multistate world is likely to be a hybrid solution, or diversified portfolio. However, a Decision Maker (DM) who is an Expected Utility (EU) maximizer would never select a diversified portfolio; s(he) would select the MEU alternative.
This paper has three objectives:
1) Identify the differences between the EUT axioms and robust critical system requirements.
2) Investigate the validity of several well-known decision models as decision aids for choosing robust critical systems.
3) Develop a realistic and mathematically valid method for defining and selecting robust critical systems.
The remainder of the paper is structured as follows. Section 2 reviews the classical paradigm for AoA in a multistate world. A simple sensor selection problem is used to illustrate the limitations of EUT for critical systems. Section 3 critically analyzes the EUT axioms with a focus on the continuity and independence axioms. Section 4 presents a paradox for the selection hybrid systems. Section 5 discusses different notions of robustness. The minimax regret and the maximin criteria are shown to be potentially misleading criteria for robustness. Section 6 briefly reviews DT. The linear disappointment model is shown to provide a credible risk-based robustness metric. Section 7 proposes an approach based on portfolio allocation with stochastic optimization as a flexible and transparent method for defining choice problems and determining hybrid solutions with desirable properties such as diversification and robustness. Section 8 provides some concluding remarks.
2. Analysis of Alternatives
2.1. Classical Paradigm
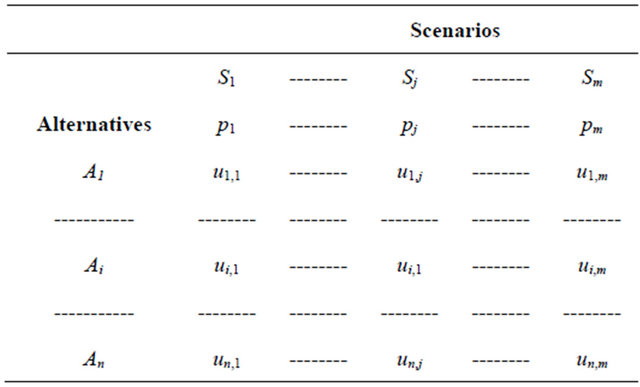
The AoA problem is modeled with a decision matrix, Table 1. The m columns represent a set of m mutually exclusive scenarios  with probabilities
with probabilities  that sum to 1. The scenarios may be chance events or willful acts by adversaries. The n rows represent a set of n alternatives
that sum to 1. The scenarios may be chance events or willful acts by adversaries. The n rows represent a set of n alternatives 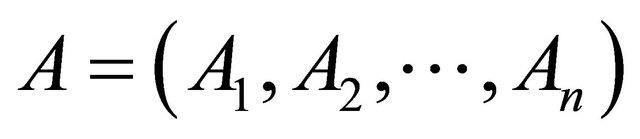 with the performance across each scenario specified in terms of the associated outcomes,
with the performance across each scenario specified in terms of the associated outcomes, . Each alternative may then be thought of as a lottery; EUT is used to choose the preferred one. The AoA proceeds as follows:
. Each alternative may then be thought of as a lottery; EUT is used to choose the preferred one. The AoA proceeds as follows:
1) The utility of a set of r mutually exclusive outcomes  with probabilities
with probabilities  is characterized by a vNM EU function4
is characterized by a vNM EU function4
Table 1. Generic decision matrix.
 (1)
(1)
2) The preference for each alternative Ai is represented by its EU,
 (2)
(2)
3) The Rational Individual should choose the alternative with the MEU,
 (3)
(3)
The validity of the above equations requires additive independence. This is unlikely to be a realistic assumption for complex systems and Systems of Systems (SoS) because there are significant interactions among attributes with the result that the whole is greater the sum of the parts. The use of simulation is preferred for realism, especially for complex systems such as SoS [19].
The outlined process, as further discussed in the subsequent sections, may also mislead practitioners to overlook hybrid solutions with desirable properties such as FARness.
2.2. Single-Sensor Selection Example
As an example, consider a modified version of the decision problem in [20, p. 36]. To make it more concrete, it is assumed that the alternatives are 4 hypothetical sensors  for a border surveillance system. For the purpose of the paper, each sensor is approximated by a cookie-cutter model [21] with detection range R0 and probability of detection PoD
for a border surveillance system. For the purpose of the paper, each sensor is approximated by a cookie-cutter model [21] with detection range R0 and probability of detection PoD that depends on three states of nature,
that depends on three states of nature, . The cookie-cutter data are specified in Table 2 columns 1-45. It is assumed that potential intruders have no intelligence of the sensor performance; they try to infiltrate the border at random times and random locations.
. The cookie-cutter data are specified in Table 2 columns 1-45. It is assumed that potential intruders have no intelligence of the sensor performance; they try to infiltrate the border at random times and random locations.
The Rational Individual who equates PoD with utility is considered to be “risk neutral”. S(he) would use Equation (1) with the values in Table 2 columns 1-4 to compute each sensor EU. Based on the values in Table 2 column 5, s(he) would select A3. The Rational Individual who is either risk-averse or risk-seeking would argue that utility rather than PoD is the appropriate measure of sensor usefulness. In accordance with EUT, s(he) would base his/her preferences on the MEU.
Utility is associated with the performance of an alternative or the consequences of an act. The evaluation of a person’s utility is a highly challenging task and for greater realism it should be experimentally solicited without invoking analytical mathematical functions [23]. The process is illustrated for a Table 2 sensor.
1) PoD = 0.5 is identified as the reference level with u(0.5) = 0. Other values are assessed relative to it.
2) Outcomes associated with PoD > 0.5 are considered gains. The corresponding utilities have a diminishing characteristic of gain satiation. For ease of perception, a scale is established with u(1.0) = 10.
3) Outcomes associated with PoD < 0.5 are considered losses. In accordance with loss aversion, the shape of the utility function is steeper than for PoD > 0.5. A lower PoD threshold may be specified to screen out unacceptable alternatives. It is assumed that u(0) = –30.
4) The utilities of a few intermediate PoD values are determined by probing the DM about his/her indifference or willingness to bet a PoDi sensor for a 50-50 gamble between a sensor with PoDh > PoDi and a sensor with PoDl < PoDi. For example, consider a DM indifferent between a PoD = 0.06 sensor and a 50-50 gamble of a PoD = 0.5 sensor or nothing, i.e. sensor with PoD = 0. This equates to

Other intermediate points are determined the same way.
5) The resulting data are depicted in Figure 1. They can be fitted with the following utility function:
Table 2. Sensor cookie-cutter model data.

 (4)
(4)
The utility values for Table 2 data are given in Table 3. Sensors A1 and A2 have unequal EUs. This reflects the fact that the utility function given by Equation (4) captures some aspects of risk aversion. The Rational Individual would select A3. The rational individual, however, might disagree with this choice because of the poor performance of A3 in state S3. S(he) would argue that this choice is not robust because it is vulnerable to attacks by adversaries who may have acquired this information [14].
3. Limitations of the EUT Axioms
3.1. Problem Formulation
As with all theoretical models, EUT has limitations. Different but logically equivalent sets of axioms have been proposed. Most rely extensively on the concept of monetary lotteries. In a 1921 lecture entitled, “Geometry and Experience,” Einstein [24, p. 233] states:
“As far as the propositions of mathematics refer to reality, they are not certain; as far as they are certain, they do not refer to reality.”
The above comment is equally relevant with “decision theory” substituted for “mathematics”.
This section follows Luce and Raiffa’s formulation [2] because it provides greater visibility of the probabilistic aspects of the EUT axioms than recent more abstract mathematical formulations. Luce and Raiffa consider five basic assumptions: 1) ordering of alternatives including transitivity; 2) reduction of compound lotteries; 3) continuity; 4) substitutability6; and 5) monotonicity. The continuity and independence axioms are of special interest because of their key roles for the derivations of Equations (1)-(3). As a result, they are analyzed to systematically assess their validity for critical systems.
Consider a generic scenario, a set of n alternatives
Table 3. Sensor utility decision matrix.

 , and r basic consequences
, and r basic consequences . In accordance with the ordering axiom, the consequences can be arranged in order of decreasing preference and numbered accordingly:
. In accordance with the ordering axiom, the consequences can be arranged in order of decreasing preference and numbered accordingly:  Every alternative can then be thought of as a lottery associated with an r-tuplet of basic consequences and probabilities q7:
Every alternative can then be thought of as a lottery associated with an r-tuplet of basic consequences and probabilities q7:
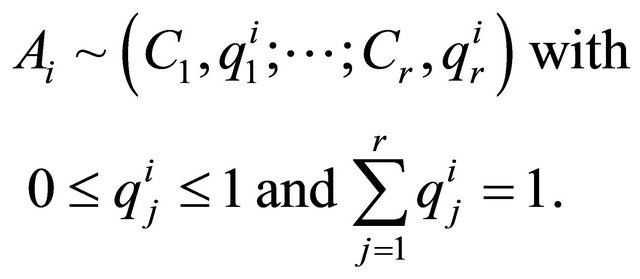 (5)
(5)
3.2. The Continuity Axiom
For each outcome Ci, the Rational Individual8 is indifferent between Ci and an alternative involving just C1 and Cr:
 (6)
(6)
Ci and  are two different entities:
are two different entities:  can be any outcome of an equivalence class with certainty equivalent Ci [25].
can be any outcome of an equivalence class with certainty equivalent Ci [25].
Context is of the essence for validity of the continuity axiom. Taken literally, the Rational Individual should be indifferent between receiving an amount of money  and the lottery
and the lottery  for some probability p. Following this observation, Luce and Raiffa [2, p. 27] write:
for some probability p. Following this observation, Luce and Raiffa [2, p. 27] write:
“When put in such bold form, some, whom we would hesitate to charge with being “irrational”, will say No... Even though the universality of the assumption is suspect, two thoughts are consoling. First, in few applications are such extreme alternatives as death present.”
Critical systems and decisions often impact life and death issues. The DM who is a rational individual cannot invoke the above loophole. S(he) needs to mindfully assess low probability events with potentially dire consequences such as serious injuries, death, and heavy financial losses. The emotionally charged aspects of such decisions render the use of the continuity axiom impractical and unrealistic.
3.3. The Independence Axiom9
For every alternative in the set A, the Rational Individual is indifferent to the substitution of an equivalent outcome

Figure 1. Evaluation of utility function.
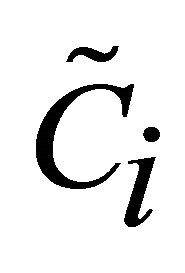 for Ci:
for Ci:
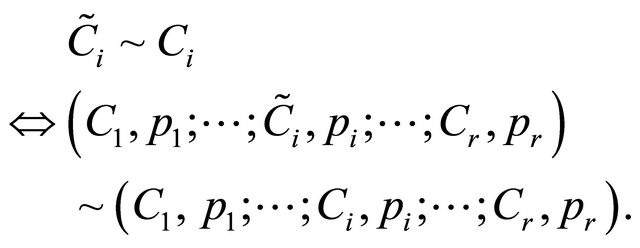 (7a)
(7a)
The independence condition given by Equation (7a) is more apparent if expressed in terms of the combination  in common with arbitrary alternatives G or H. The independence axiom then reduces to its common form,
in common with arbitrary alternatives G or H. The independence axiom then reduces to its common form,
 (7b)
(7b)
It follows from the EUT continuity and transitivity axioms that
 (7c)
(7c)
The probabilistic outcomes on the right-sides of Equations (7b) and (7c) are the mutually exclusive basic outcomes associated with Q, G and H. It would be wrong to think of them as mixtures of outcomes.
The independence axiom requires that when comparing probabilistic alternatives, the Rational Individual views the “common part” as irrelevant and preserves the original preference in accordance with Equations (7a)- (7c). This is a valid assumption if and only if there are no interaction effects including psychological influences between G and Q or H and Q. The use of decision trees is often presented as a graphical justification for the independence axiom. This argument is flawed because the folding back procedure substitutes the certainty equivalent for branches at nodes and thereby implicitly assumes that outcomes are independent. De Neuville [26, p. 366] writes:
“The axiom implies that the substitutions can occur regardless of the other opportunities in front of a person and, thus, regardless of how these substitutions alter the probabilistic distribution of the consequences.”
In conclusion, the independence axiom is in conflict with probability calculus and the rational individual who makes decisions based on the complete risk curve rather than simply the EU [27].
3.4. The Chew Weighted Utility Theory
The Chew weighted utility theory [28] replaces the independence axiom with the weak substitution axiom:
 (8)
(8)
For  , the weak substitution axiom reduces to the independence axiom, Equation (7b). The Chew weighted utility theory includes EUT as a special case. For
, the weak substitution axiom reduces to the independence axiom, Equation (7b). The Chew weighted utility theory includes EUT as a special case. For  it admits the presence of complementarities of Ai and Aj with Ak. It, therefore, provides a resolution of the Allais paradox [29] as well as the two-sensor paradox of Section 4.
it admits the presence of complementarities of Ai and Aj with Ak. It, therefore, provides a resolution of the Allais paradox [29] as well as the two-sensor paradox of Section 4.
The Chew weighted utility function for a probabilistic mixture of two alternatives H and G has the following linear functional form:
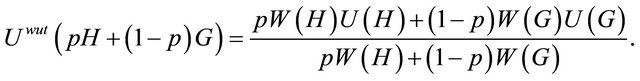 (9)
(9)
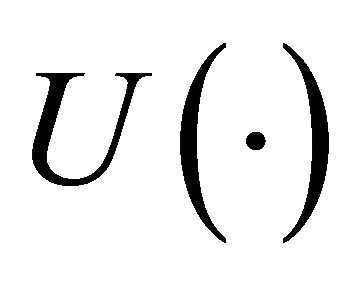 is a vNM utility function;
is a vNM utility function;  is an additional weight function that enables it to accommodate the preference patterns of several key EUT paradoxes including the Allais paradox [29]. Equation (9) reduces to Equation (1) for
is an additional weight function that enables it to accommodate the preference patterns of several key EUT paradoxes including the Allais paradox [29]. Equation (9) reduces to Equation (1) for  Constant. Otherwise, it significantly increases the complexity of EUT, which limits its applicability as a normative model for AoAs.
Constant. Otherwise, it significantly increases the complexity of EUT, which limits its applicability as a normative model for AoAs.
3.5. Choice Axioms for Catastrophic Risks
As discussed in Section 2, the EUT linear functional form causes the ranking of alternatives to be relatively insensitive to low probability scenarios. This is in conflict with the way rational individuals often choose options for a wide range of problems with low probability but catastrophic consequences. These include, but are not limited to, global environmental risks, national security, and critical infrastructures. Chichilnisky [13] proposed a set of 3 axioms to account for such choices. It results in a utility function  that includes a term that assigns positive weights to low probability events:
that includes a term that assigns positive weights to low probability events:
 (10)
(10)
where  and
and  is an additive measure with a functional form yet to be specified. Chichilnisky [13] characterizes the status of her work as follows: “The new axioms require a new calculus of variation.... Some results already exist, but much work is still needed.”
is an additive measure with a functional form yet to be specified. Chichilnisky [13] characterizes the status of her work as follows: “The new axioms require a new calculus of variation.... Some results already exist, but much work is still needed.”
4. Two-Sensor Paradox
The Section 2.2 sensors are considered for a border surveillance system of length 4R0. The problem is which two sensors to select to maximize the detection probability of potential intruders. It is assumed that the latter possess no intelligence of sensor performance; they try to infiltrate the border at random locations and times.
4.1. EUT Analysis
For the Rational Individual,
 (11)
(11)
S(he) would then conclude that the homogeneous combination  is preferable to the hybrid combination
is preferable to the hybrid combination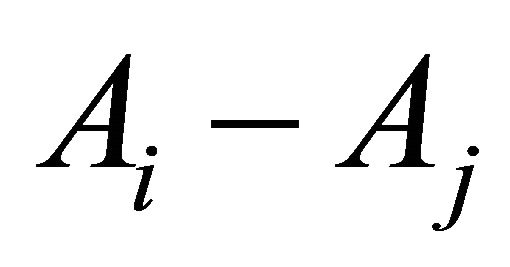 . By extending this reasoning to all sensor combinations, the Rational Individual concludes that the best combination consists only of the highest utility sensor, i.e. A3. The rational individual would disagree with this solution because it lacks diversity and it is highly vulnerable to infiltration given the low PoD in scenario S3 (see Table 2). There are several other examples of EUT paradoxes with anomalous risk behaviors [30-31].
. By extending this reasoning to all sensor combinations, the Rational Individual concludes that the best combination consists only of the highest utility sensor, i.e. A3. The rational individual would disagree with this solution because it lacks diversity and it is highly vulnerable to infiltration given the low PoD in scenario S3 (see Table 2). There are several other examples of EUT paradoxes with anomalous risk behaviors [30-31].
4.2. Two-Dimensional Preference Analysis
Given 4 alternatives, there are 10 possible two-sensor combinations to consider. Each combination  may be represented by a two-dimensional vector with the PoD utility as elements. A two-dimensional utility function is needed to represent preferences over the combinations such that
may be represented by a two-dimensional vector with the PoD utility as elements. A two-dimensional utility function is needed to represent preferences over the combinations such that
 (12)
(12)
By analogy to the determination of the sensor utility function in Section 2.2, it is assumed that 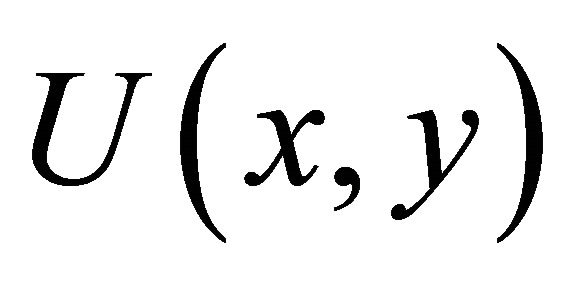 is given by treating Equation (4) as a function of the joint variable xy:
is given by treating Equation (4) as a function of the joint variable xy:
 (13)
(13)
The multiplicative form xy has advantages over the linear form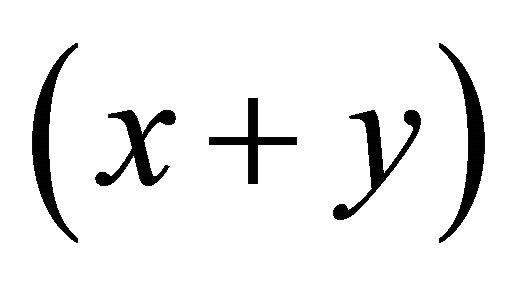 . It more realistically accounts for two-sensor vulnerabilities. Furthermore, the
. It more realistically accounts for two-sensor vulnerabilities. Furthermore, the  indifference or isoutility curves represent simple convex preferences10.
indifference or isoutility curves represent simple convex preferences10.
The utilities for the 10 two-sensor combination are computed using Equation (13) and averaged over the 3 scenarios. The results are presented in Table 4.
Table 4. Two-dimensional preference analysis.

1) . The MEU solution,
. The MEU solution, 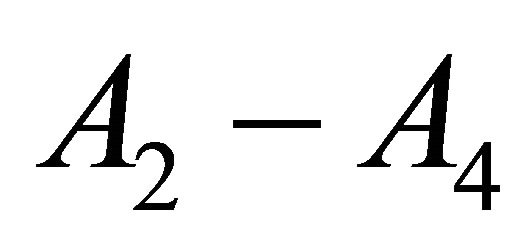 , does not consist of the two MEU alternatives. It draws on the synergistic interaction between the two alternatives.
, does not consist of the two MEU alternatives. It draws on the synergistic interaction between the two alternatives.
2)  exhibits diversification [32]. For some combinations of
exhibits diversification [32]. For some combinations of ,
,
 (14)
(14)
3) The robust combination A4-A4 ranks last. This result combined with the above two demonstrates that convex preferences exhibit diversification but that diversification is not equivalent to robustness.
A resolution of the two-sensor paradox is that EUT needs to be modified to be compatible with preference for robust and hybrid solutions. Options include 1) replacing the independence axiom with a modification such as the weak substitution axiom, or 2) introducing corrections to EUT such as DT (see Section 6).
5. Robust Solutions
5.1. Various Notions
In semi-layman parlance, robust solutions perform reasonably well and have acceptable outcomes over a wide range of plausible scenarios without assuming that “everything goes right”. The importance of robustness as a criterion for good decisions is reflected by the fact that DMs often purposefully forgo the MEU option for ones that perform well over a wide range of scenarios and are relatively insensitive to uncertainties. The professional literature contains different notions of robustness with variations that depend on the application domain.
The following three notions of robustness are of interest for critical systems consideration.
1) Lempert et al. [33] define a robust strategy as “one with relatively small regret compared to the alternatives across a wide range of plausible futures.” They evaluate the regret of long-term policies using an approach based on Savage’s minimax regret rule11.
2) Krokhmal et al. [34] advocate generating robust decision by optimizing an upper percentile of the risk probability distribution12. They note that “in this regard, risk management in military applications is similar to other fields such as finance, nuclear safety, etc., where decisions targeted at achieving the maximal expected performance may lead to an excessive risk exposure.”
3) Ullman [35] advocates developing designs with low sensitivity to noise or uncertainty in accordance with the Taguchi method. He considers performance, risk and cost among the factors that need to be addressed [35, p. 36]: “The result of a robust decision is an option chosen with known and acceptable satisfaction and risk... A major goal in making a robust decision is to eliminate all the uncertainty possible within the scope of available resources.”
This section examines Savage’s minimax regret rule as a regret-based robustness criterion. Risk-based robustness is addressed in Section 6.
5.2. The Minimax Regret Rule
Savage’s minimax regret rule is a recommendation that under uncertainty a person should choose the alternative that minimizes the maximum difference from the highest achievable utility in each scenario. The anticipated regret for choice Ai in scenario Sj depends on the other alternatives:
 (15a)
(15a)
where  is a vNM utility. Equation (15a) represents the largest possible loss for Ai in state Sj relative to the best alternative. The minimax regret choice is the alternative
is a vNM utility. Equation (15a) represents the largest possible loss for Ai in state Sj relative to the best alternative. The minimax regret choice is the alternative  with the smallest regret over all of the scenarios:
with the smallest regret over all of the scenarios:
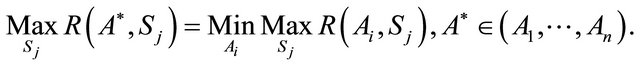 (15b)
(15b)
The minimax regret rule leads to the comparison of the Table 3 sensors in Table 5. Sensor A3 is the recommended alternative; but, it performs poorly in S3. The rational individual who seeks a robust solution is likely to reject it. The well balanced A4 ranks 3rd. These results raise serious doubts about the usefulness of the minimax regret rule as a robustness criterion13.
The maximin criterion, also known as Wald’s minimax for losses, recommends selecting the alternative with the maximum minimum utility, A4 (see Table 3). The maximin criterion and minimax regret criterion have different characteristics. The maximin criterion captures aversion to the worst possible outcome for each alternative. The minimax regret criterion is concerned with missing beneficial opportunities. Numerous analysts believe that the minimax regret criterion is preferable to the maximin criterion; this is in conflict with the above results.
6. Disappointment Theory for AoA
The term “disappointment” has psychological connotetions that are not relevant in the context of the paper. Nevertheless, it is used in the paper because it is entrenched in the decision theory literature.
6.1. General Overview
Bell [10] and Loomes and Sugden [11] proposed DT to account for the fact that rational individuals may anticipate disappointment when they counterfactually compare the outcome of an action in one scenario relative to the better outcomes in the other scenarios. The rational individual may account ex-ante for these negative feelings in decision making. Similarly, feelings of elation are associated with the better outcomes. DT, unlike RT, does not perform comparisons across alternatives. This avoids potentially misleading results of pairwise comparisons [36]. The disappointment level and utility of an alternative are therefore independent of the other alternatives.
Several DT models have been proposed as corrections to EUT. Bell [10] and Loomes and Sugden [11] assumed that for a given alternative the strength of the disappointment associated with a probabilistic outcome is measured relative to the alternative’s EU. Delquié and Cillo [37] noted that rational individuals are more likely to compare
Table 5. The minimax regret decision matrix corresponding to Table 3.

the outcome obtained against the outcomes that they failed to get had other scenarios realized. They hypothesized that the level of disappointment associated with outcome Oi depends explicitly on the probabilities and utilities of the outcomes that are preferred, i.e. the outcomes  14. The disappointment associated with alternative Aj given the realization of scenario Si, is modeled as follows:
14. The disappointment associated with alternative Aj given the realization of scenario Si, is modeled as follows:
 (16)
(16)
where  is a positive function of
is a positive function of  with
with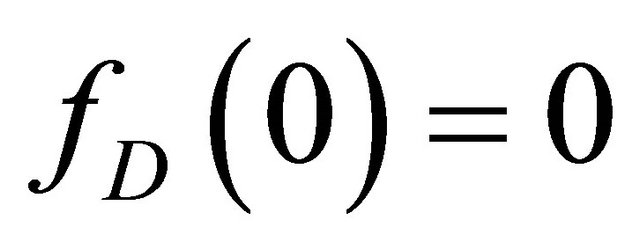 ;
;  is the probability of scenario Sk.
is the probability of scenario Sk.
6.2. Disappointment Correction to EUT
For the purpose of this paper,  in Equation (16) is assumed to be a linear function. The overall disappointment is then obtained by averaging Equation (16) over all the m scenarios. This simplified version of the Delquié and Cillo Linear Disappointment Model (LDM) [37] modifies the vNM EU, Equation (2), as follows:
in Equation (16) is assumed to be a linear function. The overall disappointment is then obtained by averaging Equation (16) over all the m scenarios. This simplified version of the Delquié and Cillo Linear Disappointment Model (LDM) [37] modifies the vNM EU, Equation (2), as follows:
 (17)
(17)
where d is a positive constant that captures the rational individual’s sensitivity to disappointment.
Equation (17) has several notable properties:
1) The functional form is similar to the vNM EU but with rank-dependent weighted probabilities.
2) The second term represents downside risk15 relative to the best possible outcome. It provides a credible measure of risk-based robustness.
3) The parameter d can be varied to reflect varying degrees of risk tolerance and thereby identify alternatives with unacceptable consequences.
6.3. Two-Sensor Selection Example
The two-sensor paradox of Section 4 is analyzed using the LDM. Given that disappointment is explicitly accounted for, the analysis uses the Table 2 physical data. The results for d = 0.8 are presented in Table 6. Figure 2 compares several two-sensor combinations versus d.
The results are consistent with a rational preference for diversification and the notion of risk-based robustness. The two-sensor combinations change rank as d varies. For d > 0.7, A4-A4 rank 1st and A2-A4 ranks 2nd. A3-A3 changes rank from 1st for d = 0 to last for d > 0.6. To reach a final decision, a risk-averse DM would peruse Figure 2 and chooses between.A2-A4 or A4-A4 depending on preferences for risk tolerance and diversification.
The LDM16 analysis is simpler and more intuitive than the utility theory two-dimensional preference analysis of Section 4.2. It can readily be extended to complex combinations of multiple constituents. However, all available DT models lack a mathematical basis for developing complex hybrid solutions or portfolios. Such an approach is presented in the next section.
7. Portfolio Optimization for Robustness
7.1. General Formulation
As discussed in Sections 4-6, a risk-adverse DM is likely to prefer a hybrid solution that performs relatively well over all scenarios of interest rather than a homogeneous solution consisting solely of the MEU alternative. Consider a situation of n alternatives  and m mutually exclusive probabilistic scenarios
and m mutually exclusive probabilistic scenarios . A hybrid solution may be thought of as a portfolio characterized by a multidimensional probability distribution function [39]
. A hybrid solution may be thought of as a portfolio characterized by a multidimensional probability distribution function [39]
Table 6. Results using the linear disappointment model.


Figure 2. Comparison of selected two-sensor combinations versus disappointment parameter d using the linear disappointment model.
 (19a)
(19a)
where  is the decision vector of allocation variables with xi being the Ai allocation fraction. The multidimensional function
is the decision vector of allocation variables with xi being the Ai allocation fraction. The multidimensional function  is a generalized discrete probability distribution with values being probability distributions functions (pdf) rather than point estimates.
is a generalized discrete probability distribution with values being probability distributions functions (pdf) rather than point estimates.  is a pdf that models the Ai outcome17 for scenario Sj.
is a pdf that models the Ai outcome17 for scenario Sj.
The determination of the decision vector x may be specified in terms of the following stochastic optimization problem:
Maximize the zth percentile of PHS(x), Equation (19a), subject to the normalization, scenario performance, and affordability constraints, Equations (19b)-(19d):
 (19b)
(19b)
 (19c)
(19c)
 (19d)
(19d)
The values z and f are percentiles18 that a DM specifies in accordance with his/her risk tolerance; aj is his/her lowest acceptable value for the fth percentile for performance in scenario Sj; Ci is the Ai cost; N0 is the number of required systems; and B0 is the available budget. Equation (19d) can accommodate pdfs for Ci with an agreed-to percentile for the cost constraint [27].
The above formulation provides a flexible and transparent way for the analyst and DM to define the choice problem and generate mixed solutions with desirable properties such as diversification and robustness19.
7.2. Hybrid Solution Example
The above approach is applied to the design of a robust border surveillance system of N0 sensors using the four Table 2 sensors. The problem is to determine the combination of sensors , Equation (19a), that maximizes the expected PoD over the three scenarios
, Equation (19a), that maximizes the expected PoD over the three scenarios subject to the normalization constraint, Equation (19b), and
subject to the normalization constraint, Equation (19b), and  for the performance constraint, Equation (19c). The budget is assumed not to be a constraint. The hybrid solution data are summarized in Table 7 and its cumulative distribution [41] and several of interest are depicted in Figure 3.
for the performance constraint, Equation (19c). The budget is assumed not to be a constraint. The hybrid solution data are summarized in Table 7 and its cumulative distribution [41] and several of interest are depicted in Figure 3.
Table 7. Sensor hybrid solution optimized for robustness.
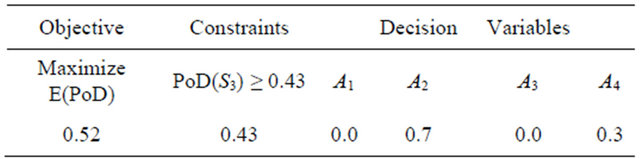

Figure 3. Cumulative distributions for the hybrid sensor solution (HS) optimized for robustness, its constituent sensors A2 and A4, and the MEU alternative A3.
The hybrid solution is robust: 1) the associated cumulative distribution is narrower than those of the homogeneous alternatives, 2) the minimum PoD = 0.4, and 3) there is a 80% probability that the PoD ³ 0.5 for the identified scenarios. Given the Table 2 alternatives, this is the solution that a DM who desires some level of robustness at an acceptable performance cost is likely to intuitively prefer. Diversity provides additional benefits such as defense against common-cause failures [42] and increased deterrence against attackers [14].
The solution to this example is obvious. Nevertheless, it illustrates the significant advantages and benefits of portfolio allocation with stochastic optimization for developing robust critical systems. Solving complex realworld problems will require tools with integrated Monte Carlo simulation and stochastic optimization capabilities. They are available in commercial and proprietary versions. For information purposes, Crystal Ball® with OptQuest® was applied to the illustrative example. OptQuest® is a general purpose optimizer developed to effectively solve complex stochastic, nonlinear, and combinatorial optimization problems [43].
8. Conclusions
The paper begins by analyzing the suitability of EUT for AoAs of critical systems in a multistate world. The concept of robust solutions is discussed within the context of multiple scenarios. Several well-known models are compared for a simplified example of choosing sensors for a hypothetical border surveillance system. Portfolio allocation with stochastic optimization is proposed and demonstrated to be a valid and realistic method for defining robust critical systems.
Some of the key conclusions are:
1) The EUT is inadequate for critical systems AoA because MEU alternatives may possess vulnerabilities that could be exploited and/or are susceptible to common-cause failures. The continuity axiom is unrealistic given the emotionally charged aspects of critical decisions. The independence axiom is in conflict with the rational individual who is not an expected utility maximizer and prefers to make decisions using risk curves.
2) The two-sensor paradox raises serious doubts about the validity of the minimax regret rule as a robustness criterion for decision making under risk and the belief that it is superior to the maximin rule. Both have serious problems and are potential misleading for choosing critical systems.
3) If the utility is linear in the probabilities, the EU of a hybrid solution cannot be greater than the EU of every constituent alternative. A GEUT and nonlinear utility functions are required to exhibit robustness and diversification.
4) The LDM simply modifies the vNM EU by adding a term proportional to downside risk. The results of the two-sensor selection example confirm that it is a promising model for choosing robust homogeneous solutions. However, the LDM and other available DT models do not provide a mathematical basis for developing hybrid solutions.
5) Portfolio allocation with stochastic optimization provides a flexible and transparent approach for defining the choice problem and determining hybrid solutions for critical systems with desirable properties such as diversification and robustness. The best combination does not necessarily consist of the alternatives with the highest EUs; it draws on the strengths and complementarities that any of the alternatives can provide.
6) The composition of the hybrid solution is determined by optimizing a specified percentile of the system performance subject to robustness and cost constraints. Performance and cost uncertainties can be modeled using realistic pdf’s.
Ultimately, the selection of robust solutions depends on the identified alternatives. Critical systems require analysis that is mindful of the following considerations: 1) the limitations of EUT and GEUT models; 2) risk-mitigation properties such as FARness; and 3) the importance of hybrid solutions as options. Given the availability of commercial and proprietary tools with integrated Monte Carlo simulation and stochastic optimization capabilities, the future direction is the implementation of the proposed portfolio allocation with stochastic optimization as a practical design and analysis tool for complex systems and SoS on actual projects.
9. Acknowledgments
This work was stimulated by a Naval Postgraduate School capstone project prepared by the 2008 Cohort from the Naval Surface Warfare Center Dahlgren Division (NSWCDD) and the Naval Undersea Warfare Center Division Newport [44]. The author thanks Neil Baron, Distinguished Scientist NSWCDD, for insightful comments on hybrid solutions.
[1] EFERENCES
[2] US Office of Homeland Security, “The National Strategy for Homeland Security,” 2002. http://www.ncs.gov/library/policy_docs/nat_strat_hls.pdf
[3] R. D. Luce and H. Raiffa, “Games and Decisions: Introduction and Critical Survey,” Dover Publications, New York, 1957.
[4] J. von Neumann and O. Morgenstern, “Theory of Games and Economic Behavior,” 2nd Edition, Princeton University Press, Princeton, 1947.
[5] L. J. Savage, “The Foundations of Statistics,” 2nd Revised Edition, Dover Publications, New York, 1972.
[6] P. C. Fishburn, “Normative Theories of Decision Making under Risk and Uncertainty,” In: D. Bell, H. Raiffa and A. Tversky, Eds., Decision Making: Descriptive, Normative, and Prescriptive Interactions, Cambridge University Press, Cambridge, 1988, pp. 78-98. doi:10.1017/CBO9780511598951.006
[7] D. Kahneman and A. Tversky, “Prospect Theory: An Analysis of Decisions under Risk,” Econometrica, Vol. 47, No. 3. 1979, pp. 263-291. doi:10.2307/1914185
[8] A. Tversky and D. Kahneman, “Advances in Prospect Theory: Cumulative Representation of Uncertainty,” Journal of Risk and Uncertainty, Vol. 5, No. 4, 1992, pp. 297-323.
[9] D. E. Bell, “Regret in Decision Making under Uncertainty,” Operations Research, Vol. 30, No. 5, 1982, pp. 961-981. doi:10.1287/opre.30.5.961
[10] G. Loomes and R. Sugden, “Regret Theory: An Alternative Theory of Rational Choice under Uncertainty,” Economic Journal, Vol. 92, No. 368, 1982, pp. 805-824. doi:10.2307/2232669
[11] D. E. Bell, “Disappointment in Decision Making under Uncertainty,” Operations Research, Vol. 33, No. 1, 1985, pp. 1-27. doi:10.1287/opre.33.1.1
[12] G. Loomes and R. Sugden, “Disappointment and Dynamic Consistency in Choice under Uncertainty,” Review of Economic Studies, Vol. 53, No. 2, 1986, pp. 271-282. doi:10.2307/2297651
[13] E. Dekel and B. L. Lipman, “How (Not) to Do Decision Theory,” Annual Review of Economics, Vol. 2, No. 1, 2010, pp. 257-282. doi:10.1146/annurev.economics.102308.124328
[14] G. Chichilnisky, “An Axiomatic Approach to Choice under Uncertainty with Catastrophic Risks,” Resource and Energy Economics, Vol. 22, No. 3, 2000, pp. 221- 231. doi:10.2139/ssrn.1522307
[15] G. G. Brown and L. A. Cox Jr., “Making Terrorism Risk Analysis Less Harmful and More Useful: Another Try,” Risk Analysis, Vol. 31, No. 2, 2011, pp. 193-195. doi:10.1111/j.1539-6924.2010.01563.x
[16] P. K. Davis, R. D. Shaver and J. Beck, “Portfolio-Analysis Methods for Assessing Capability Options,” RAND, Santa Monica, 2008.
[17] S. Savage, “The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty,” John Wiley & Sons, Hoboken, 2009.
[18] Y. Y. Haimes, “Risk Modeling, Assessment, and Management,” 3rd Edition, John Wiley & Sons, Hoboken, 2009.
[19] H. M. Markowitz, “Portfolio Selection: Efficient Diversification of Investments,” 2nd Edition, Blackwell, Cambridge, 1997.
[20] Office of the Deputy under Secretary of Defense for Acquisition and Technology, Systems and Software Engineering, “Systems Engineering Guide for Systems of Systems,” Version 1.0, ODUSD(A&T)SSE, Washington, 2008.
[21] D. H. Wagner, W. C. Mylander and T. J. Sanders, “Naval Operations Analysis,” 3rd Edition, Naval Institute Press, Annapolis, 1999.
[22] A. Washburn and M. Kress, “Combat Modeling,” Springer, New York, 2009. doi:10.1007/978-1-4419-0790-5
[23] 2011 Naval Surface Warfare Center Crane Cohort, “System Engineering Approach to Improving Arizona Border Patrol C4ISR Mission Operations,” MSSE Capstone Project, Naval Postgraduate School, Monterey, 2011.
[24] R. Hastie and R. M. Dawes, “Rational Choice in an Uncertain World: The Psychology of Judgment and Decision Making,” Sage Publications, Thousand Oaks, 2001.
[25] A. Einstein, “Ideas and Opinions,” Bonanza Books, New York, 1954.
[26] E. Malinvaud, “Note on von Neumann-Morgenstern’s Strong Independence Axiom,” Econometrica, Vol. 20, No. 4, 1952, p. 679. doi:10.2307/1907650
[27] R. de Neuville, “Applied Systems Analysis: Engineering Planning and Technology Management,” McGraw-Hill, New York, 1999.
[28] E. Kujawski, M. Alvaro and W. Edwards, “Incorporating Psychological Influences in Probabilistic Cost Analysis,” Systems Engineering, Vol. 7, No. 3, 2004, pp. 195-216. doi:10.1002/sys.20004
[29] S. H. Chew, “Axiomatic Utility Theories with the Betweenness Property,” Annals of Operations Research, Vol. 19, No. 1, 1989, pp. 273-298. doi:10.1007/BF02283525
[30] M. Allais, “Le Comportement de l’Homme Rationnel devant le Risque: Critique des Postulats et Axiomes de l’Ecole Américaine,” Econometrica, Vol. 21, No. 4, 1953, pp. 503-546. doi:10.2307/1907921
[31] P. Samuelson, “Risk and Uncertainty: A Fallacy of Large Numbers,” Scientia, Vol. 98, No. 4, 1963, pp. 108-113.
[32] M. Rabin and R. H. Thaler, “Anomalies: Risk Aversion,” The Journal of Economic Perspectives, Vol. 15, No. 1, 2001, pp. 219-232. doi:10.1257/jep.15.1.219
[33] E. Dekel, “Asset Demands without the Independence Axiom,” Econometrica, Vol. 57, No. 1, 1989, pp. 163-169. doi:10.2307/1912577
[34] R. J. Lempert, D. G. Groves, S. W. Popper and S. C. Bankes, “A General, Analytic Method for Generating Robust Strategies and Narrative Scenarios,” Management Science, Vol. 52, No. 4, 2006, pp. 51-528. doi:10.1287/mnsc.1050.0472
[35] P. Krokhmal, R. Murphey, P. Pardalos, S. Uryasev and G. Zrazhevsky, “Robust Decision Making: Addressing Uncertainties in Distributions,” In: S. Butenko, et al., Eds., Cooperative Control: Models, Applications and Algorithms, Kluwer Academic Publishers, Dordrecht, 2003, pp. 165-185.
[36] D. G. Ullman, “Making Robust Decisions: Decision Management for Technical, Business, & Service,” Trafford Publishing, Victoria, 2006.
[37] G. Friedman, “The Intransitivity of Pairwise Comparisons Even with a Single Rational Decision Maker or: Homomorphisms from Allegedly Paradoxical Dice to Decision-Making in the Military, Business and Sports World,” Presentation to the NSF Decision-Based Design Workshop, Long Beach, 1999. http://dbd.eng.buffalo.edu/papers/friedman.html
[38] P. Delquié and A. Cillo, “Disappointment without Prior Expectation: A Unifying Perspective on Decision under Risk,” Journal of Risk and Uncertainty, Vol. 33, No. 3, pp. 197-215. doi:10.1007/s11166-006-0499-4
[39] D. Nawrocki, “A Brief History of Downside Risk Measures,” Journal of Investing, Vol. 8, No. 3, 1999, pp. 9-25. doi:10.3905/joi.1999.319365
[40] E. Kujawski and G. A. Miller, “Quantitative Risk-Based Analysis for Military Counterterrorism Systems,” Systems Engineering, Vol. 10, No. 4, 2007, pp. 273-289. doi:10.1002/sys.20075
[41] D Bertsimas, D. B. Brown and C. Caramanis, “The Theory and Applications of Robust Optimization,” SIAM Review, Vol. 53, No. 3, 2011, pp. 464-501. doi:10.1137/080734510
[42] M. Levy, “Almost Stochastic Dominance and Efficient Investment Sets,” American Journal of Operations Research, Vol. 2, No. 3, 2012, pp. 313-321. doi:10.4236/ajor.2012.23038
[43] E. Kujawski, I. M. Jacobs and A. M. Smith, “An Evaluation of the Use of Signal Validation Techniques as a Defense against Common-Cause Failures,” Electric Power Research Institute, Palo Alto, 1987.
[44] F. Glover, M. Laguna and R. Martí, “Scatter Search,” In: A. Ghosh and S. Tsutsui, Eds., Advances in Evolutionary Computation: Theory and Applications, Springer-Verlag, New York, 2003, pp. 519-537.
[45] 2008 Cohort from the Naval Surface Warfare Center Dahlgren Division and the Naval Undersea Warfare Center Division Newport, “Enhanced Vessel Awareness Capability,” MSSE Capstone Project, Naval Postgraduate School, Monterey, 2011.
NOTES
2The terms “outcome”, “consequence”, and “performance” are used interchangeably throughout the paper.
3In the paper, the term “rational individual” with lower cases “r” and “i” is used to refer to the person who uses reason and emotions to make decisions in a systematic and logical manner with due consideration to the personal and social context.
4There is homomorphism between the vNM EU function and the linear additive assumption of Multicriteria Decision Analysis (MCDA); e.g. the weights in MCDA and the probabilities in EUT.
5The analysis can be extended to incorporate sensor physical properties based on experimental data [22].
6It is commonly referred to as the independence axiom.
7The variables p and q denote probabilities in different contexts. The variable p denotes scenario probabilities. The variable q denotes the probabilities of the basic outcomes associated with alternatives. Equation (5) refers to a generic scenario and a scenario index has been omitted with no loss of generality.
8The original vNM EUT axioms did not explicitly refer to the “Rational Individual”.
9The independence axiom is not one of the original vNM axioms. Malinvaud [25] showed that it had been implicitly assumed.
10The key property of convex preferences is that any point on the straight line joining two points on the same indifference curve has a higher utility than either point. A person with convex preferences prefers mixes of goods to extremes.
11Savage [4, p. 163] objected to use of the term “regret” and used “loss” instead. Referring to “regret”, he writes “that term seems to me to be charged with emotion and liable to lead to such misinterpretation as that the loss necessarily becomes known to the person”.
12The percentile is one of several mathematical criteria used for “conditional value-at-risk”.
13For completeness, it is noted that there are other serious problems with the minimax regret rule that can lead to irrational choices [4,26].
14The outcome Oi is associated with scenario Si. It is convenient to number the outcomes, and thereby the scenarios, in order of decreasing preference. This ordering is used throughout the section.
15Downside risk is a proven measure for characterizing portfolio risk [38].
16Simplicity and descriptive realism are two key objectives of DT [10, 11].
17Given complex systems, realistic scenario outcomes have significant uncertainties that need to be accounted for distinct from the scenario probabilities.
18Expected values are included.
19“Robustness,” as used in this paper (see Section 5), is an attribute of the solution or decision. It is not to be confused with “robust optimization,” which refers to an optimization approach where the uncertainty model is not stochastic, but set-based [40].