Effects of Sampling between Data of Significant Wave Height for Intensity and Duration of Severe Sea Storms ()
1. Introduction
A sea storm is a sequence of sea states, in which the significant wave height exceeds a fixed threshold, whose value depends on the considered location [1-3]. In the Mediterranean Sea, the storm threshold may be considered even equal to 1.5 m: this value cannot be considered in most locations in the oceans. A general definition of sea storm was proposed by Boccotti [4-7].
Statistical properties of waves in a sea storm were investigated by Borgman [8,9], who determined the cumulative distribution function of the maximum wave height in a sea storm through an integral form. This result is very important for long-term analysis of extreme waves, based on the concept of extremes during a sea storm. For example, the Equivalent Triangular Storm model [4], as well as the Equivalent Power Storm model [10], represents a storm by means of two parameter: the former giving the intensity of the storm, the latter the duration of the storm.
Both models enable to determine, with an analytical approach, the long-term statistics of severe storms [4-7, 10]. A key parameter for these approaches is given by the storm duration, which is estimated by starting from the sequence of storms in a given location (considering a time span greater than several years).
In this paper some storms are investigated, both in the Central Mediterranean Sea and in the Atlantic and Pacific Ocean. Data of Italian buoys network and of NOAANational Data Buoy Center (USA) are processed.
The storm analysis is proposed by considering different values of the sampling Δt between two consecutive records, varying in the range (0.5 - 6 hours). The sensitivity analysis of the model with the variation of Δt is proposed, to determine how this time interval modifies the intensity and the duration of the sea storms. Finally, some comments are given on the effect of the results on long-term modeling by applying the equivalent storm approaches [4-7,10,11].
2. Sea Storms
A sea storm is defined as a sequence of sea states in which the significant wave height  exceeds a given threshold. In general, the storm starts when
exceeds a given threshold. In general, the storm starts when  has an up-crossing related to the given storm threshold and ends when Hs goes down this threshold.
has an up-crossing related to the given storm threshold and ends when Hs goes down this threshold.
Following Boccotti [4], we may define a sea storm as “a sequence of sea states in which the significant wave height exceeds the threshold  and does not fall below this threshold for a continuous time interval greater than 12 hours”.
and does not fall below this threshold for a continuous time interval greater than 12 hours”.
This storm definition enables to take into account that a “calm” period may occur even during a storm: if this period, in which  is below the threshold
is below the threshold , has duration smaller than 12 hours we have a single storm. If this time is greater than 12 hours, we consider two different storms.
, has duration smaller than 12 hours we have a single storm. If this time is greater than 12 hours, we consider two different storms.
Regarding the storm threshold, it must depend upon the given location. It may be considered proportional to the average value  of the significant wave height. Boccotti [4-7] proposed a storm threshold equal to 1.5 times
of the significant wave height. Boccotti [4-7] proposed a storm threshold equal to 1.5 times . A higher value of this threshold, for example 2 or 3 times
. A higher value of this threshold, for example 2 or 3 times  may be assumed: in this case we have a lower number of storms.
may be assumed: in this case we have a lower number of storms.
2.1. Statistical Properties of Waves in a Sea Storm
Let us consider a storm given by a sequence of Ns sea states, with different values of significant wave height and peak/mean period.
The cumulative distribution function, defined as the probability to have the maximum wave height in the sea storm smaller than a given threshold H is given by:
 (1)
(1)
where  is the sea state duration,
is the sea state duration,  the mean period [12] and
the mean period [12] and
 (2)
(2)
[4] is the probability that a wave has height larger than H in a sea state with significant wave height Hs equal to h. The narrow bandedness parameter  is the ratio, in absolute value, between the absolute minimum and the absolute maximum of the covariance function of the sea state. The parameter
is the ratio, in absolute value, between the absolute minimum and the absolute maximum of the covariance function of the sea state. The parameter  is equal to 1 for an infinitely narrow spectrum, 0.73 for a mean JONSWAP spectrum [13] and 0.65 for a Pierson-Moskowitz spectrum [14].
is equal to 1 for an infinitely narrow spectrum, 0.73 for a mean JONSWAP spectrum [13] and 0.65 for a Pierson-Moskowitz spectrum [14].
Following Borgman [8,9], Equation (1) may be rewritten in the integral form as
 (3)
(3)
where D is the storm duration.
The maximum expected wave height  in the sea storm is achieved as the integral over
in the sea storm is achieved as the integral over  of the probability of exceedance
of the probability of exceedance .
.
2.2. Bi-Parametric Models for Sea Storms
Sea storms may be obtained from a time series of significant wave height at a given location. Then, a bi-parametric model may be applied to determine the properties of each storm: the former will define the intensity of the storm; the latter the duration.
2.2.1. Equivalent Triangular Storm Model
The ETS model associates a triangle to each actual storm. The height a of the triangle represents the storm intensity and is equal to the maximum significant wave height during the actual storm. The base b of the triangle represents the storm duration, and it is such that the maximum expected wave height is the same in the actual storm and in the triangular storm.
Note that the height a is achieved from the storm history directly, whereas the base b is determined with an iterative procedure. Starting from the calculated value of the expected wave height in the actual storm , and from the height a of the ETS, we fix a tentatively value b' of the base of the ETS in order to calculate:
, and from the height a of the ETS, we fix a tentatively value b' of the base of the ETS in order to calculate:
 (4)
(4)
which is the maximum expected value of the wave height in a triangular storm with height a and base b'.
Then, if  of the actual storm is greater than
of the actual storm is greater than , the base b will be greater than b'; if
, the base b will be greater than b'; if , then b < b'.
, then b < b'.
The ETS model was introduced by Boccotti [4] for the long-term statistics of ocean waves and then applied by Arena & Pavone [6,7] for the long-term modeling of nonlinear crest heights and for the achievement of a generalized approach for extreme waves during storms.
2.2.2. Equivalent Power Storm Model
The Equivalent Power Storm model generalizes the concept of triangular storm: the significant wave height in time domain, during a storm, is represented with a λ power law (λ > 0), as
 (5)
(5)
where the peak of the storm (equal to a) occurs at t = 0. For a given value of λ, the EPS is defined by means of the height a and the base  which is achieved through the iterative procedure described for the ETS (see Section (2.2.1)).
which is achieved through the iterative procedure described for the ETS (see Section (2.2.1)).
The maximum expected wave height in a power λ storm with height a and base , is
, is
 (6)
(6)
The EPS model was introduced by Fedele & Arena [10] to give a better representation of the storms, and for the extreme values of wave heights. They showed that the EPS model has a good stability for λ > 0.7. Furthermore, the value of λ characterizes the storm: we have a parabolic storm for λ = 2, a cubic storm for λ = 3, a cuspstorm for λ = 0.5 and so on. For λ = 1 we have triangular storms. Fedele & Arena [10] showed that the optimal value λ, for the modeling of extreme sea storms, is 0.75.
2.3. Application of ETS and EPS Models for Long-Term Modeling of Extreme Storms
Let us consider the return period R(Hs > h) of a sea storm in which the maximum significant wave height is greater than h. The solution for R(Hs > h), by considering the EPS model, was derived by Fedele and Arena [7]. It is given by the equation
 (7)
(7)
where  is the mean base for given height a (which provides the relation between the mean value of the bases b and the heights a of the EPSs by means of a regression) and
is the mean base for given height a (which provides the relation between the mean value of the bases b and the heights a of the EPSs by means of a regression) and 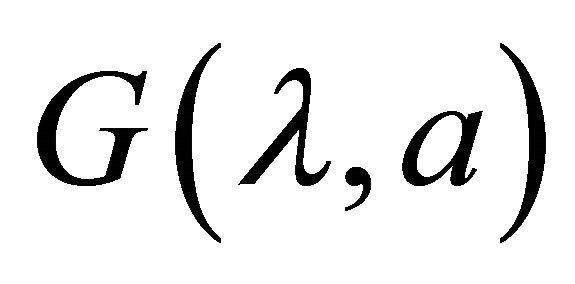 is a function related to the probability density function of the EPS heights.
is a function related to the probability density function of the EPS heights.
The expression of  is highly dependent on the location under examination. Analysis of several data has shown that the mean base-height regression formula
is highly dependent on the location under examination. Analysis of several data has shown that the mean base-height regression formula
 (8)
(8)
may be applied for estimation of R(Hs > h), where Ka and Kb are location-dependent parameters; note that Ka is a length like a, and Kb has the dimension of time (it is in hours if b is in hours). The function  is defined in [10].
is defined in [10].
Equation (8) is very important for the calculation of return values of significant wave height for fixed values of the return period. Then, analysis of the variability of the storm bases, and then of the regression (8) is important for applications.
3. Analysis of Severe Storms, Recorded by NOAA (USA) and RON (Italy) Buoys
In the paper some buoys are considered from both the NOAA-NDBC (National Oceanic and Atmospheric Administration’s-National Data Buoy Center) network (USA) and the Italian buoys network (RON—Rete Ondametrica Nazionale—managed by ISPRA).
The NOAA manages the NDBC, which consists of a network with many buoys moored along the US coasts, both in the Pacific Ocean and in the Atlantic Ocean. Some buoys were moored in the seventies, so that more than 30 years of data are available. The historical wave data consists in significant wave height, peak and mean period, given with a sampling between two consecutive records equal to one hour. Only few buoys are directional.
In the paper the NOAA buoys 46066, 46028, 46035, 46085, 46001 are considered in the Pacific Ocean and the buoys 41048, 44001, 44005, 44008, 44011 in the Atlantic Ocean.
The Italian buoys network (RON) started measurements in 1989, with 8 directional buoys located off the coasts of Italy. Currently, the network consists of 15 buoys, moored in deep water. The time Δt between two consecutive records, during storms, is half an hour; for each record, the data of significant wave height, peak and mean period and dominant direction are given. In the Central Mediterranean Sea, the buoys of Alghero, Mazara del Vallo, Ponza, Cetraro and Crotone are considered.
3.1. Data Analysis
The analysis of severe sea storms in the Mediterranean Sea and in the Atlantic and Pacific Ocean is proposed by processing as input data the significant wave height time series, respectively, from both buoys of RON network and buoys of the NOAA.
The analysis is carried out by applying both the equivalent triangular storm (ETS) model and the equivalent power storm (EPS) model, assuming different values of the time intervals Δt between two consecutive records. It is considered a Δt value ranging between 0.5 and 6 hours for the RON data, and between 1 and 6 hours for the NDBC data.
In the Mediterranean Sea, the strongest storm recorded from 1989 to 2005 has been identified and analyzed, for each location. For Alghero, which is characterized by the severest wave climate in Italian Sea, 25 storms have been processed.
For the Atlantic and Pacific Ocean, 10 buoys have been considered and for each of them, the most intense storm recorded during the last three years has been identified and analyzed.
For the most severe actual storm, recorded at each considered location, both in the Mediterranean sea and in the Oceans, the Equivalent Triangular Storm (λ = 1) and the Equivalent Power Storm (for values of the shape parameter λ equal to 0.5, 0.75, 2, 3) have been determined by considering a time interval Δt between two consecutive records equal to 1, 3, 6 hours. These elaborations are given in Figure 1 for five storms of the NDBC-NOAA buoys and in Figure 2 for five buoys of the RON storms. We may appreciate the sensitivity of the base and the height of each storm for increasing value of Δt of interest for application (that is Δt up to 6 hours, which is a value widely used in meteorological models).
All data have been processed in order to achieve the intensity and duration of the sea storms.

Figure 1. Five storms recorded by NOAA-NDBC buoys in the Atlantic and Pacific Oceans. They are the severest storms recorded at the considered buoys in the last three years, and the relative EPS calculated for different values of λ, between 0.5 and 3. First column shows each storm obtained for a time span between two records of 1hour; the second and third columns show the storm for 3 and 6 hours respectively.
It is found, in agreement with [10], that b decreases for increasing values of λ. This is a systematic trend, observed from all storms.
Regarding the effect of variation of time Δt between two successive records, we have found that the mean base bm of the storm increases for increasing values of Δt.

Figure 2. Five storms recorded by RON buoys in the Central Mediterranea Sea. They are the severest storms recorded at the considered buoys in the last three years, and the relative EPS calculated for different values of λ, between 0.5 and 3. First column shows each storm obtained for a time span between two records of 1hour; the second and third columns show the storm for 3 and 6 hours respectively.
Table 1 summarizes these results: we may compare the mean values of the storm duration, for a given values of λ, for different Δt.
Note that the analysis has been carried out starting from the smallest values of Δt available from significant wave height time series (that is Δt = 0.5 hours for RON buoys and Δt = 1 hour for NOAA buoys). To increase the value of Δt the data has been partially analyzed: starting from the full time series, with Δt = 0.5 hours for RON, the analysis for Δt = 1 hour is done by considering a value of Hs every two, for Δt = 3 hours a value of Hs every six and so on. Each time series, with a given value of Δt, has been then processed to analyze the properties of the storm.
In the Figure 3, a scatter diagram is shown with the duration (parameter b of the associated equivalent storm)for the whole set of analyzed storms recorded at the considered locations, which has been calculated with different values of the time interval Δt between two consecutive records, for any fixed value of the shape parameter λ. We observe that, for both the Mediterranean and the Oceans, the duration of a sea storm tends to increase as greater Δt is.
In Figure 4 the analysis of the storm duration when the interval Δt between two consecutive records varies, has been carried out for Alghero by considering the 25

Figure 3. Duration of the most intense storms recorded at the considered buoys of the NOAA-NDBC and of the RON, calculated with different values of the time interval Δt between two consecutive records, for a fixed value of the shape parameter λ.

Figure 4. Duration of the 25 most intense storms recorded at Alghero (Italy by the RON), calculated with different values of the time interval Δt between two consecutive records, for a fixed value of the shape parameter λ.
most intense storms. It is confirmed that for fixed sea storm, its duration grows when Δt increases.
For what concerns the storm intensity (parameter a of the associated equivalent storm), from Figure 5 it is evi-

Figure 5. Intensity of storms for different values of time Δt between two consecutive records. (a) Alghero buoy; (b) NOAA-NDBC and RON buoys.
Table 1. Mean values bm of the storm duration, for a given values of λ, for different Δt.

dent that, considering a time interval between two consecutive records greater than 1 hour, the peak of the storm is not always well identified. The maximum significant wave height can be smaller than that one actually occurred at the apex of the storm. This difference increases as greater Δt is.
4. Conclusions
The paper has shown the comparison among some severe storms, recorded by buoys of NOAA-NBDC network in the Atlantic and Pacific Oceans and by RON Italian network, in the Central Mediterranean Sea. The equivalent power storm (EPS) model has been applied for representing the storms by means of a given power law, which may be linear (with λ = 1 power), giving a triangular storm, or a parabolic (λ = 2), a cubic (λ = 3), a cusp (λ = 0.5) storm.
It has been shown how the structure of the storms changes with different values of the time span Δt between two following records. The RON gives actually records each 0.5 hours, while the NOAA-NODC each hour.
The variability of the intensity and duration of the storms, represented with the EPS model, has been investtigated, for increasing value of time Δt between two records in the range (0.5, 6 hours). Value of 6 hours is widely used for analysis of significant wave heights from meteorological models (for example, the WAMECMWF).
The result is that for increasing values of Δt two variations (errors) appears: the storm duration is increased significantly, and the storm intensity may be smaller. This error may be important for long-term analysis based in the ETS or EPS models.
It is recommended, for the statistics of extreme waves during storms, the use of continuous records (Δt = 0.5 hours) or of Δt = 1 hour, because the error is negligible.
A future work will regard the development of a new wave station for coastal zone [15], for monitoring continuous values of Hs which will be able to investigate the individual waves in sea storms.
NOTES