Methods for Lower Approximation Reduction in Inconsistent Decision Table Based on Tolerance Relation ()
1. Introduction
The rough set theory, proposed by Pawlak in the early 1980s [1], is an extension of the classical set theory for modeling uncertainty or imprecision information. The research has recently roused great interest in the theoretical and application fronts, such as machine learning, pattern recognition, data analysis, and so on.
Attribute reduction is one of the hot research topics of rough set theory. Much study on this area had been reported and many useful results were obtained [2-8]. However, most work was based on consistent information systems, and the main methodology has been developed under equivalence relations (indiscernibility relations). In practice, most of information systems are not only inconsistent, but also based on tolerance relations because of various factors. The tolerance of properties of attributes plays a crucial role in those systems. For this reason, J. Jarinen [9-13] proposed an extension rough sets theory, called the rough sets based on tolerances to take into account the tolerance relation properties of attributes. This innovation is mainly based on substitution of the indiscernibility relation by a tolerance relation. And many studies have been made in DRSA [14-18]. But useful results of attribute reductions are very poor in inconsistent information systems based on tolerance relations until now.
In this paper, the lower approximation reduction is proposed in inconsistent information systems based on tolerance relations. Moreover, some properties are discussed. Furthermore, judgment theorem and discernibility matrix are obtained, from which an approach to lower approximation reductions can be provided in inconsistent information systems based on tolerance relations.
2. Rough Sets and Information Systems Based on Tolerance Relations
The following recalls necessary concepts and preliminaries required in the sequel of our work. Detailed description of the theory can be found in [5,17].
An information system with decisions is an ordered quadruple , where
, where
 is a non-empty finite set of objects;
is a non-empty finite set of objects;
 is a non-empty finite attributes set;
is a non-empty finite attributes set;
 denotes the set of condition attributes;
denotes the set of condition attributes;
 denotes the set of decision attributes, and
denotes the set of decision attributes, and ;
;
 ,
,  is the value of
is the value of 
for ,
,  is the domain of
is the domain of , where
, where ;
;
 ,
,  is the value of
is the value of
 for
for ,
,  is the domain of
is the domain of ,
, .
.
If a binary relation T on the universe U is reflexive and symmetric, it is called a tolerance relation on U. The set of all tolerance relations on U is denoted by . A tolerance relation T can construct a covering of the universe U, not a partition. For any tolerance relation
. A tolerance relation T can construct a covering of the universe U, not a partition. For any tolerance relation  and
and  denote
denote
 ;
;
 ;
;
where  means x and
means x and  have the tolerance
have the tolerance , or
, or  and
and  haven’t the tolerance
haven’t the tolerance , and the
, and the  is called the tolerance neighborhood or tolerance class of the object
is called the tolerance neighborhood or tolerance class of the object .
.
An information system is called an information system based on tolerance relations, in brief TIS, if all relations of condition attributes are tolerance relations.
In general, we call an information system based on tolerance relations with decision to be a decision table based tolerance relations, denoted by , that is
, that is  . Thus the following definition can be obtained.
. Thus the following definition can be obtained.
Definition 2.1. Let  be a decision table based on tolerance relations, for any
be a decision table based on tolerance relations, for any , denote
, denote  and
and  are tolerance relations of information system
are tolerance relations of information system .
.
If we denote
 ;
;
 then the following properties of a tolerance relation are trivial.
then the following properties of a tolerance relation are trivial.
Proposition 2.1. Let  be a tolerance relation. The following hold.
be a tolerance relation. The following hold.
(1)  is reflexive, symmetric, but not transitive, so it is not an equivalence relation.
is reflexive, symmetric, but not transitive, so it is not an equivalence relation.
(2) If , then
, then .
.
(3) If , then
, then 
(4) 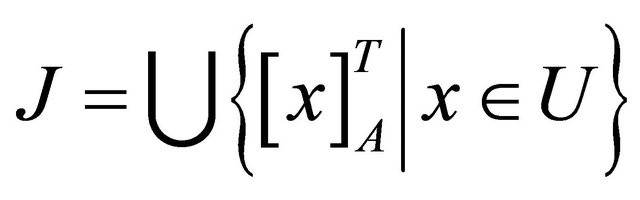 constitutes a covering of
constitutes a covering of .
.
For any subset  of
of , and
, and  of
of  define
define
 ;
;
 ,
,
 and
and  are said to be the lower and upper approximation of
are said to be the lower and upper approximation of  with respect to a tolerance relation
with respect to a tolerance relation . And the approximations have also some properties which are similar to those of Pawlak approximation spaces.
. And the approximations have also some properties which are similar to those of Pawlak approximation spaces.
Proposition 2.2. Let  be an information systems based on tolerance relation and
be an information systems based on tolerance relation and , then its lower and upper approximations satisfy the following properties.
, then its lower and upper approximations satisfy the following properties.
(1)
(2) 
(3) 
(4) 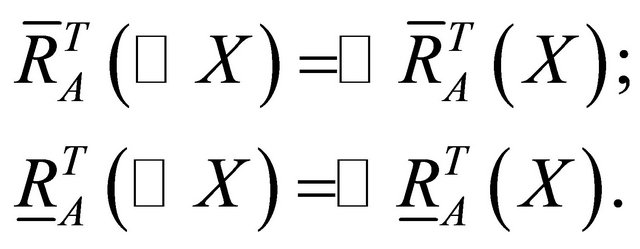
(5) 
(6) If , then
, then  and
and  ;
;
where  is the complement of
is the complement of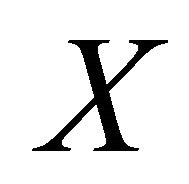 .
.
Definition 2.2. For an information system based on tolerance relations with decisions 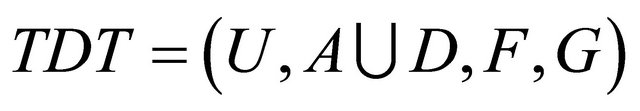 , if
, if , then this information system is consistent, otherwise, this system is inconsistent.
, then this information system is consistent, otherwise, this system is inconsistent.
Example 2.1. Given an information system based on tolerance relations in Table 1.
Define the tolerance relation  as following:
as following:

From the table, we have

and
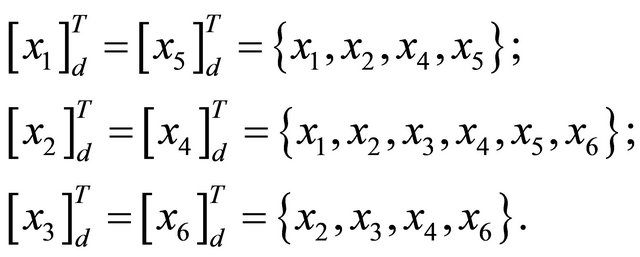
Obviously, by the above, we have , so the system in Table 1 is inconsistent.
, so the system in Table 1 is inconsistent.
For simple description, the following information system with decisions is based on tolerance relations, i.e. information systems based on tolerance relations.
3. Theories of Lower Approximation Reduction in Inconsistent Information Systems Based on Tolerance Relation
Let  be an information system based on tolerance relations with decisions, and
be an information system based on tolerance relations with decisions, and
Table 1. An information system based on tolerance relations.

 be tolerance relations derived from condition attributes set
be tolerance relations derived from condition attributes set  and decision attributes set
and decision attributes set  respectively. For
respectively. For , denote
, denote


where . Furthermore, we said
. Furthermore, we said  is the lower approximation function about attributions sets B.
is the lower approximation function about attributions sets B.
Definition 3.1. Let  and
and  be two vectors with
be two vectors with  dimensions. If
dimensions. If , we said that
, we said that  is equal to
is equal to , denoted by
, denoted by . If
. If , we said that
, we said that  is less than
is less than , denoted by
, denoted by . Otherwise, If it exists
. Otherwise, If it exists  such that
such that , we said
, we said  is not less than
is not less than , denoted by
, denoted by .
.
Such as , and
, and .
.
From the above, we can have the following propositions immediately.
Proposition 3.1. Let  be an information system based on tolerance relations with decisions. If
be an information system based on tolerance relations with decisions. If , then
, then .
.
Definition 3.2. Let 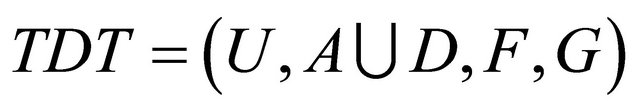 be an Inconsistent information system. If
be an Inconsistent information system. If , for all, we say that
, for all, we say that  is a lower approximation consistent set of
is a lower approximation consistent set of . If
. If  is a lower approximation consistent set, and no proper subset of
is a lower approximation consistent set, and no proper subset of  is lower approximation consistent set, then
is lower approximation consistent set, then  is called an lower approximation consistent reduction of
is called an lower approximation consistent reduction of .
.
Example 3.1. Consider the system in Table 1.
For the system in Table 1, we denote

We can have
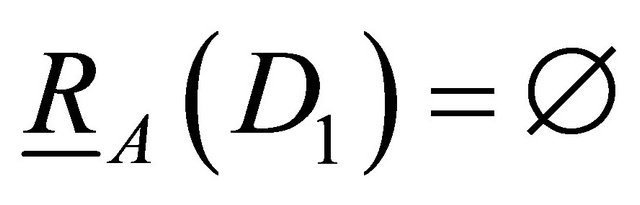


When , it can be easily checked that
, it can be easily checked that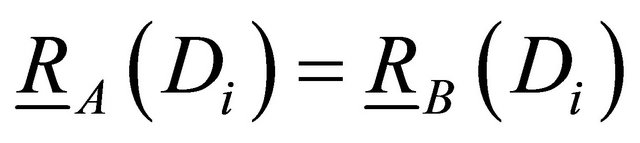 , for all
, for all . So that
. So that  , and
, and  is a lower approximation consistent set of
is a lower approximation consistent set of . Furthermore, we can examine that
. Furthermore, we can examine that  and
and  are not lower approximation consistent set of
are not lower approximation consistent set of . That is to say
. That is to say  is a lower approximation reduction of
is a lower approximation reduction of .
.
Moreover, it can be easily calculated that  and
and  are not lower approximation consistent sets of
are not lower approximation consistent sets of . Thus there exist only one lower approximation reduction of
. Thus there exist only one lower approximation reduction of  in the system of Table 1, which is
in the system of Table 1, which is .
.
In the following, detailed judgment theorems of lower approximation reduction are obtained.
4. Methods for Attribute Reduction in Inconsistent Information Systems Based on Tolerance Relations
This section provides approaches to lower approximation reduction in inconsistent information systems.
Definition 4.1. Let 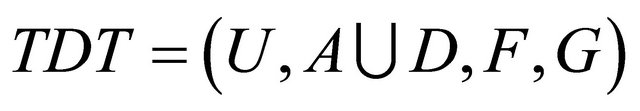 be an information system, Denote
be an information system, Denote


 is called lower approximation discernibility attribute set, and matrixes
is called lower approximation discernibility attribute set, and matrixes
 is referred to lower approximation discernibility matrix of
is referred to lower approximation discernibility matrix of 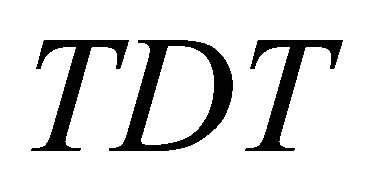 respectively.
respectively.
Theorem 4.1. Let  be an information system,
be an information system,  , then
, then 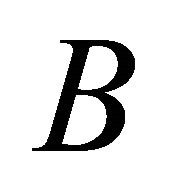 is a lower approximation consistent set
is a lower approximation consistent set  if
if  , then exists
, then exists 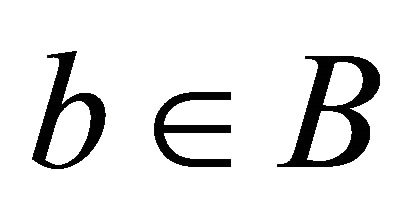 such that
such that , for any
, for any .
.
Proof.  Assume that exists
Assume that exists , for any
, for any , and
, and , if
, if , then
, then
 .
.
Since B is a lower approximation consistent set, therefore, for any , we can have
, we can have
 . According to
. According to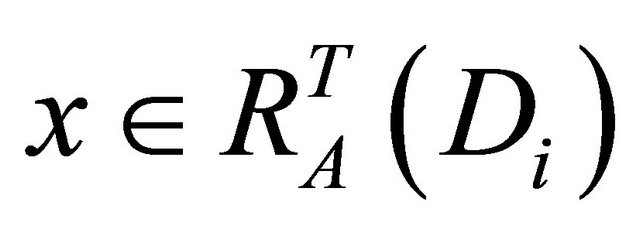 , so we can obtain
, so we can obtain  and
and . Moreover for
. Moreover for
 , then
, then , therefore
, therefore  and
and
 . Hence we have
. Hence we have , which is contradiction.
, which is contradiction.
 Supposed that
Supposed that  isn’t a lower approximation consistent set, then exists
isn’t a lower approximation consistent set, then exists , such that
, such that
 , therefore exists
, therefore exists  and
and
 . So we can have
. So we can have  and
and
 .
.
Moreover,  , so there exists
, so there exists 
and , i.e.
, i.e. . In addition, we can have that exists
. In addition, we can have that exists  such that
such that , which is contradict with
, which is contradict with .
.
Therefore  is a lower approximation consistent set.
is a lower approximation consistent set.
Theorem 4.2. Let  be an information system.
be an information system. , then
, then  is a lower approximation consistent set if and only if for any
is a lower approximation consistent set if and only if for any , we can have
, we can have .
.
Proof.  For any
For any , there exists
, there exists  such that
such that , so according to Theorem 4.1, we can have that exists
, so according to Theorem 4.1, we can have that exists  such that
such that , so
, so .
.
Therefore, if 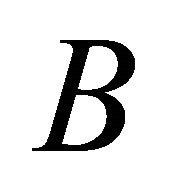 is a lower approximation consistent set then for any
is a lower approximation consistent set then for any , we can have
, we can have  .
.
 If for any
If for any ,
,  , then exists
, then exists 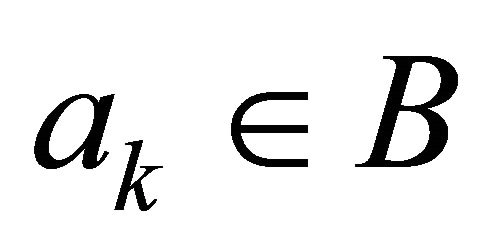 such that
such that , so we have
, so we have
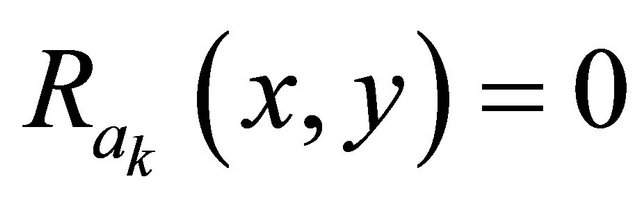 , and
, and .
.
Therefore  is a lower approximation consistent set according to Theorem 4.1.
is a lower approximation consistent set according to Theorem 4.1.
Definition 4.2. Let 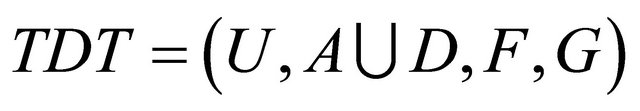 be an information system,
be an information system,  is referred to lower approximation discernibility matrix of
is referred to lower approximation discernibility matrix of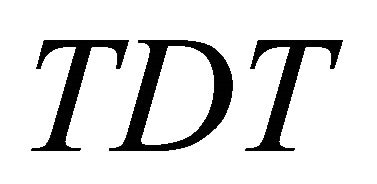 , denote
, denote

 is called discernibility formula of lower approximation.
is called discernibility formula of lower approximation.
Theorem 4.3. Let  be an information system. The minimal disjunctive normal form of discernibility formula of lower approximation is
be an information system. The minimal disjunctive normal form of discernibility formula of lower approximation is

Denote , then
, then
 is just set of all distribution reductions of
is just set of all distribution reductions of .
.
Proof. It follows directly from Theorem 4.1 and the definition of minimal disjunctive normal of the discernibility formula of lower approximation.
Theorem 4.3 provides a practical approach to lower
Table 2. Lower approximation discernibility matrix ML.

approximation reductions of information systems with decisions based on tolerance relation. The following we will consider the system in Table 1 using this approach.
Example 4.1. For the system in Table 1, the function of distribution and maximum distribution have been obtained in Example 3.1. In additional, we can have
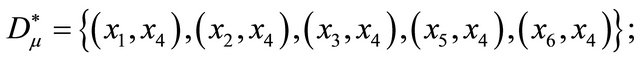
The above table (Table 2) is the lower approximation discernibility matrix of system in Table 1.
Consequently, we have

Therefore, we obtain that  is all lower approximation reduction of information system in Table 1, which accords with the result of Example 3.1.
is all lower approximation reduction of information system in Table 1, which accords with the result of Example 3.1.
5. Conclusion
It is well known that most of information systems are not only inconsistent, but also based on tolerance relations because of various factors in practice. Therefore, it is important to study the lower approximation reduction in inconsistent information systems. In this paper, we are concerned with approaches to the problem. The lower approximation reduction is introduced in inconsistent information systems based on tolerance relations. The judgment theorem and discernibility matrix are obtained, from which we can provide the approach to attribute reductions in inconsistent information systems based on tolerance relations.