1. Introduction
Many Special matrix functions appear in connection with statistics [1], mathematical physics, theoretical physics, group representation theory, Lie groups theory [2] and orthogonal matrix polynomials are closely related [3-5]. The hypergeometric matrix function has been introduced as a matrix power series and an integral representation and the hypergeometric matrix differential equation in [6-9] and the explicit closed form general solution of it has been given in [10]. The author has earlier studied the Kummer’s and Horn’s  matrix function of two complex variables under differential operators [11-13]. In [14-16], extension to the matrix function framework of the classical families of p-Kummer’s matrix function,
matrix function of two complex variables under differential operators [11-13]. In [14-16], extension to the matrix function framework of the classical families of p-Kummer’s matrix function,  and q-Appell matrix function and Humbert matrix function have been proposed.
and q-Appell matrix function and Humbert matrix function have been proposed.
Throughout this paper for a matrix  in
in , its spectrum
, its spectrum  denotes the set of all the eigenvalues of
denotes the set of all the eigenvalues of . If
. If  is a matrix in
is a matrix in , its two-norm denoted by
, its two-norm denoted by  is defined by [17]
is defined by [17]
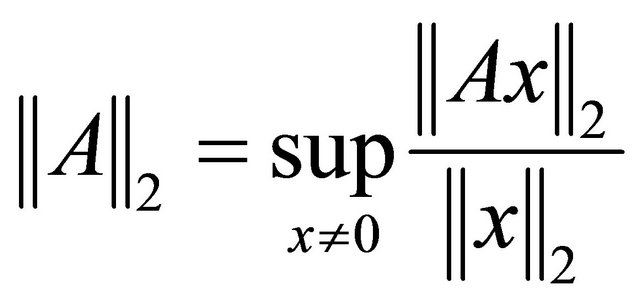
where for a vector 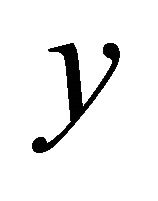 in
in ,
,  is the Euclidean norm of
is the Euclidean norm of .
.
If 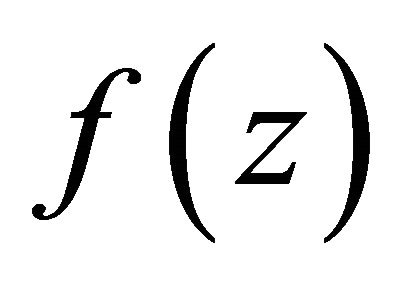 and
and  are holomorphic functions of the complex variable
are holomorphic functions of the complex variable , defined in an open set
, defined in an open set  of the complex plane, and if
of the complex plane, and if  and
and  are a matrix in
are a matrix in  with
with 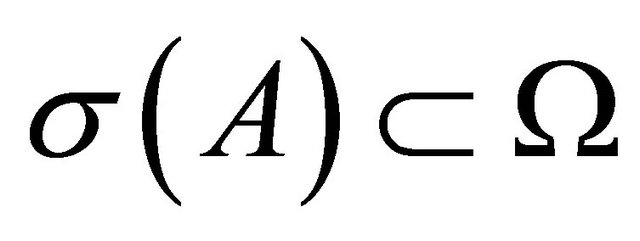 and
and  also and if
also and if , then from the properties of the matrix functional calculus [18], it follows that
, then from the properties of the matrix functional calculus [18], it follows that
 (1.1)
(1.1)
The reciprocal gamma function denoted by
 is an entire function of the complex variable
is an entire function of the complex variable . Then for any matrix
. Then for any matrix  in
in , the image of
, the image of  acting on
acting on  denoted by
denoted by  is a well defined matrix. Furthermore, if
is a well defined matrix. Furthermore, if
 (1.2)
(1.2)
where  is the identity matrix in
is the identity matrix in , then
, then  is invertible, its inverse coincides with
is invertible, its inverse coincides with  and one gets [6]
and one gets [6]
 (1.3)
(1.3)
Jódar and Cortés have proved in [6], that
 (1.1)
(1.1)
2. On pl(m, n)-Kummer Matrix Function
We We define the pl(m, n)-Kummer matrix function  of two complex variables in the form
of two complex variables in the form
 (2.1)
(2.1)
where
 ,
,
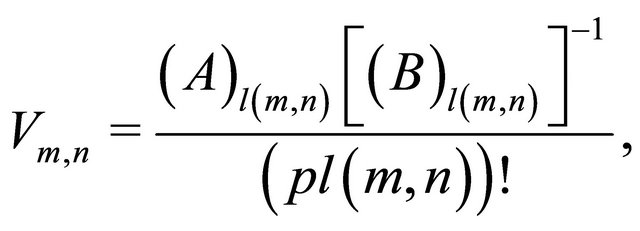
 [19] and
[19] and ,
,  and
and
 are non-negative integer numbers. Notice that
are non-negative integer numbers. Notice that  is a non-negative integer number.
is a non-negative integer number.
For simplicity, we can write the 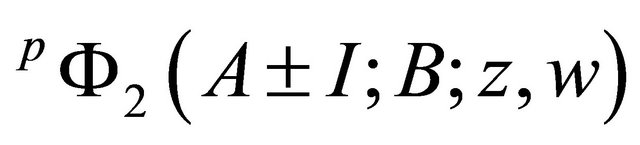 in the form
in the form ,
,  in the form
in the form  and
and  in the form
in the form .
.
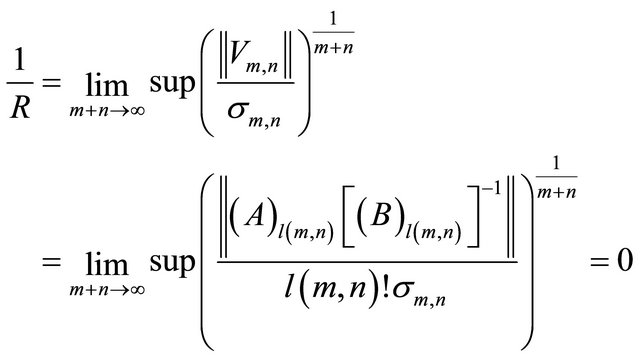
We begin the study of this function by calculating its radius of regularity  of such function for this purpose we recall relation (1.3.10) of [19] and keeping in mind that
of such function for this purpose we recall relation (1.3.10) of [19] and keeping in mind that . Hence
. Hence

where

Summarizing, the following result has been established.
Theorem 2.1. Let  and
and  be matrices in
be matrices in  such that
such that  are invertible for all integer
are invertible for all integer  . Then, the pl(m, n)-Kummer matrix function is an entire function.
. Then, the pl(m, n)-Kummer matrix function is an entire function.
For , we have
, we have
i.e., the l(m, n)-Kummer matrix function is an entire function.
Some matrix recurrence relations are carried out on the pl(m, n)-Kummer matrix function. In this connection the following matrix contiguous functions relations follow, directly by increasing or decreasing one in original relation
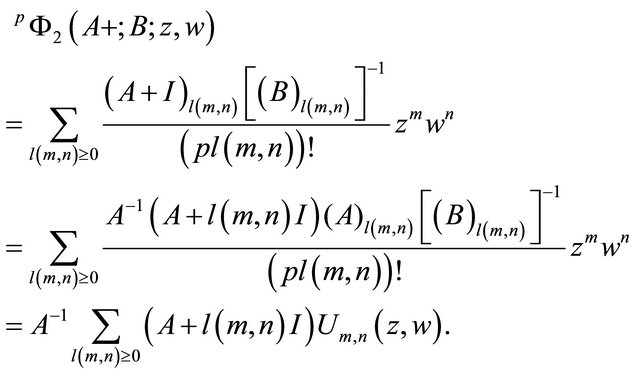
(2.2)
Similarly
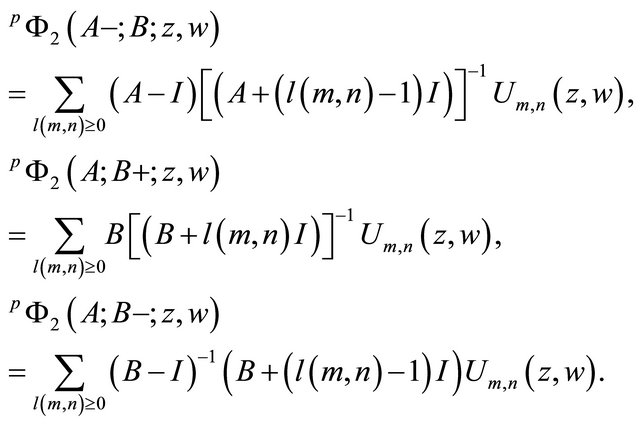 (2.3)
(2.3)
By the same way, we have
 (2.4)
(2.4)
Now, we consider the following differential operators
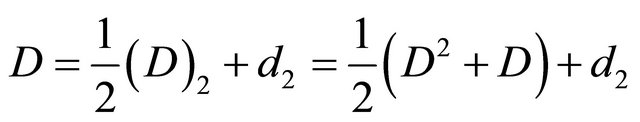
where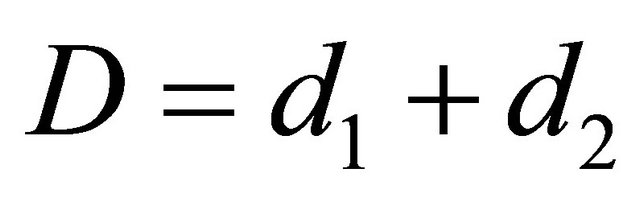 ,
, 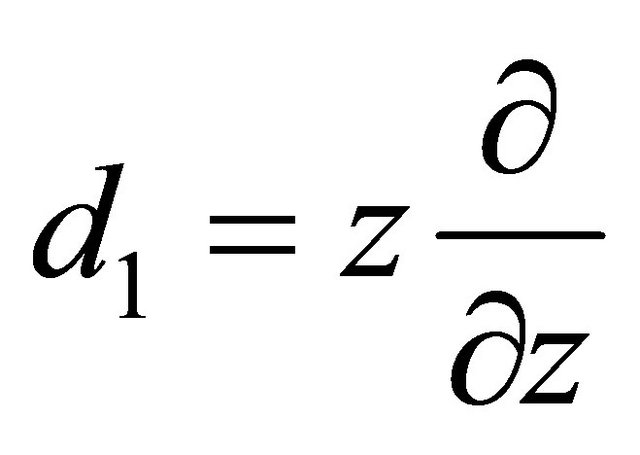 and
and .
.
It is clear that
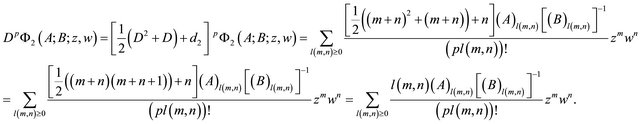
(2.5)
So that
 (2.6)
(2.6)
Putting in this relation  and
and  instead of
instead of  and
and  respectively, then
respectively, then
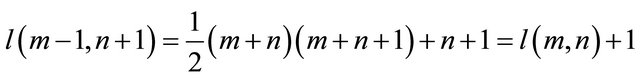
and so that we can be written the relation  and
and  instead of
instead of  and
and  yields
yields

Therefore, the power series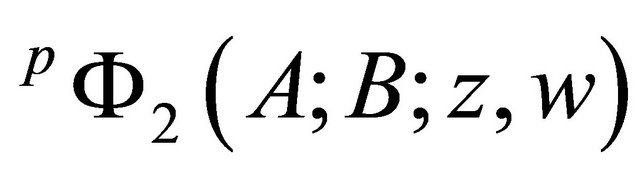 , as follows
, as follows

i.e., the pl(m, n)-Kummer matrix function is a solution of the matrix differential equation
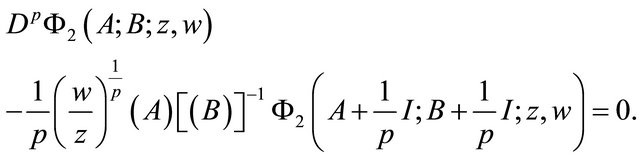
(2.7)
In this paper, we affect by differential operator D the pl(m, n)-Kummer matrix function, successively, then we have

i.e. the (m, n)-Kummer matrix function is a solution to this matrix differential equation
 (2.8)
(2.8)
Then

Therefore, the following result has been established.
Theorem 2.2. Let  and
and  be matrices in
be matrices in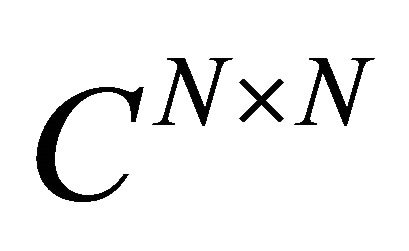 . Then the pl(m, n)-Kummer matrix function is solution of this matrix differential equation
. Then the pl(m, n)-Kummer matrix function is solution of this matrix differential equation
 (2.9)
(2.9)
The  differential operator has been defined by Sayyed [19] in the form
differential operator has been defined by Sayyed [19] in the form
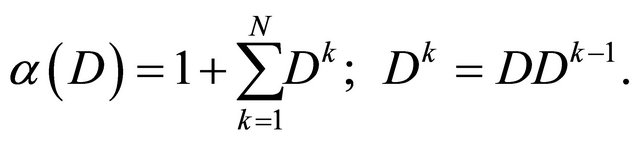
From (2.1), (2.3) and (2.5), we obtain

(2.10)
hence
 (2.11)
(2.11)
and
 (2.12)
(2.12)
Thus by mathematical induction, we have the following general form

(2.13)
where  is a finite positive integer.
is a finite positive integer.
Special cases: we can be written the matrix function  in the form
in the form
 (2.14)
(2.14)
we see that
i.e., the  is a solution to this matrix differential equation
is a solution to this matrix differential equation
 (2.15)
(2.15)
Also

i.e., the  is a solution for the matrix partial differential equations
is a solution for the matrix partial differential equations

The results of this paper are variant, significant and so it is interesting and capable to develop its study in the future. One can use the same class of differential operators for some other function of several complex variables. Hence, new results and further applications can be obtained.
3. Acknowledgements
The Author expresses his sincere appreciation to Dr. M. S. Metwally, (Department of Mathematics, Faculty of Science (Suez), Suez Canal University, Egypt) for his kind interest, encouragements, help, suggestions, comments and the investigations for this series of papers.
The author would like to thank the referees for his comments and suggestions on the manuscript.