1. Introduction
[1] presented a quantitative basis for differentiating straight, meandering, and braided channel patterns based on relationships between slope and discharge. [2] noted that an increase in the ratio of bed material load to total sediment load with a corresponding increase in channel gradient leads to a decrease in stability and hence causing channel patterns to shift from a meandering to braided channel form. [3] argued that the pattern of a river channel changes from meandering to braiding with increasing flow strength. [4] observed that the lower limit of sinuosity of a meandering river is 1.5 and larger width-depth ratios characterize braided rivers. According to [5] channel stability depends on river bed angle, sediment size and meander formation rate. [6] argued that straight streams are relatively stable and are characterized by small sediment size, low velocities and low gradient. [7] developed sediment routing models to examine changes in channel width and planform, effects of sediment pulses and landscape evolution. For width-depth ratio of up to 100, [8] used physics-based linear model to predict whether reducing or enlarging the width of a river will lead to meandering, transition from meandering to braiding or braided planform. Figure 1 was used by [9] in summarizing stability of a river channel.
Using depth (H)-width (B) ratio, longitudinal slope (S) and froude number (F), [10] observed that; braiding occurs when , meander-braid transition falls in the region
, meander-braid transition falls in the region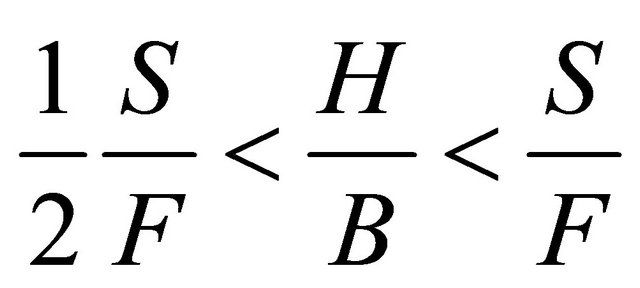 , meandering develops when
, meandering develops when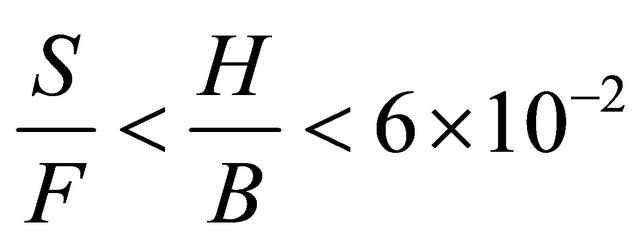 , transition to straight falls in the region
, transition to straight falls in the region  and channels remain straight when
and channels remain straight when .
.
Secondary currents represent circulation of fluids around the axis of the primary flow [11]. This leads to movement of fluid particles on a circular path which referred to as spiral motion. Helical flow consists of spiral motion superimposed on the primary flow [12]. It has long been recognized that periodically reversing helical motion is fundamental characteristic of flow in meandering rivers. Therefore the velocity and the phase shift

Figure 1. Channel classification and relative stability as hydraulic factors are varied. Source: [9].
angle of the secondary current from the channel axis displacement plays a critical role in determining meander pattern and stability of a river channel. Based on secondary current theory, there is no mathematical model that has been generated to classify river channels using the width-depth ratio and the phase shift angle. A small-perturbation stability analysis is developed for investigation of the role of the secondary current in the development of meanders and hence in classifying a river channel. It’s shown that river channel changes from straight to meandering and then from meandering to braiding as the phase shift angle reduces. Instability increases with decrease in phase shift angle and meander growth dominates downstream meander migration at small phase shift angle and vice versa.
2. Analytical Model
A channel with a finite value of the radius of curvature is considered. The radius of curvature assumes an infinite value where the channel is straight. The analysis of flow in curved channels as presented herein is restricted to sub-critical flow with hydrostatic pressure distribution and the channel depth is assumed to be much less than the width and the radius of curvature. This is mostly observed at the lower course of a river channel. In deriving the equation of motion, a differential element of fluid in polar coordinate system is used as shown in Figure 2.
[13] used force-momentum equations in polar cylindrical coordinates to relate the longitudinal velocity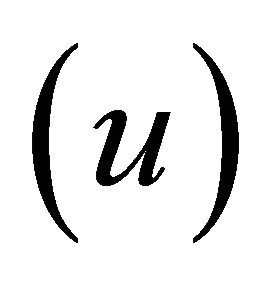 ,
,

Figure 2. Transverse velocity profile in curved channel.
transverse velocity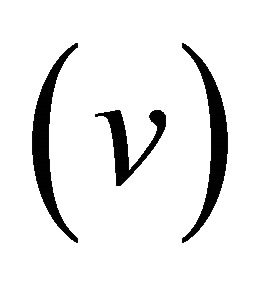 , vertical velocity
, vertical velocity , the longitudinal slope
, the longitudinal slope , transverse water surface slope (Sr), transverse shear stress (τr), longitudinal shear stress (τs) and radius of curvature
, transverse water surface slope (Sr), transverse shear stress (τr), longitudinal shear stress (τs) and radius of curvature 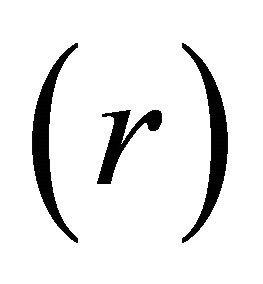 as follows:
as follows:
 (1)
(1)
 (2)
(2)
For steady flow, the time derivatives 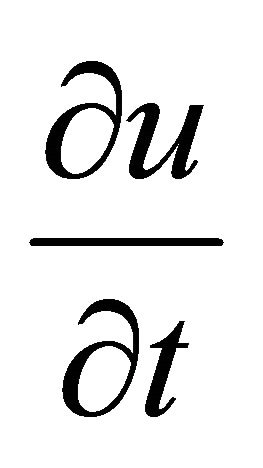 and
and  in Equations (1) and (2) can be dropped. Also second order terms
in Equations (1) and (2) can be dropped. Also second order terms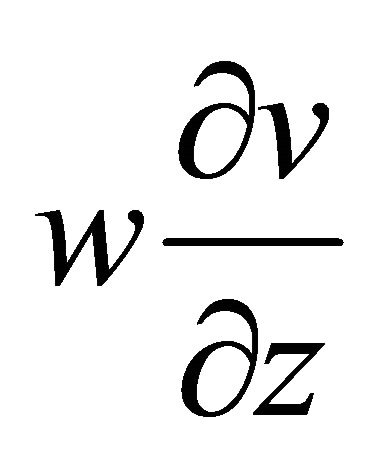 ,
,  ,
,  , and
, and  can be eliminated because
can be eliminated because 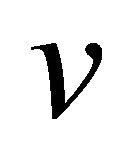 and
and 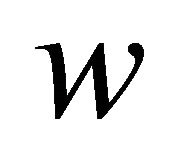 are small compared with u. Substituting all these in Equation (2), yields;
are small compared with u. Substituting all these in Equation (2), yields;
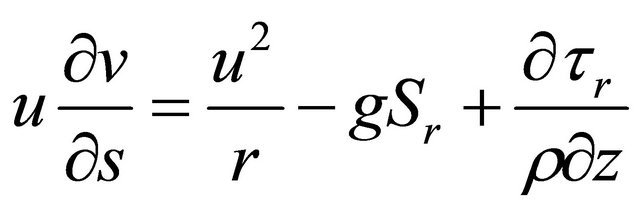 (3)
(3)
Equation (3) represents fluid motion in the transverse direction. The mechanism of secondary flow development can be described by each term of Equation (3). The left-hand side in Equation (3) is longitudinal variation of transverse velocity. In the right-hand side, the first term represents centrifugal acceleration, the second term represents the transverse water-surface slope and the third term represents the turbulent shear. From Equation (3) the transverse water surface velocity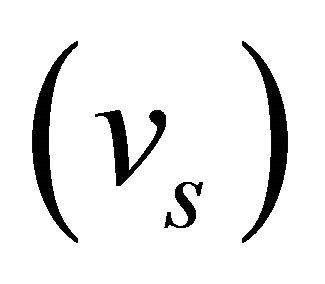 , longitudinal water surface velocity
, longitudinal water surface velocity 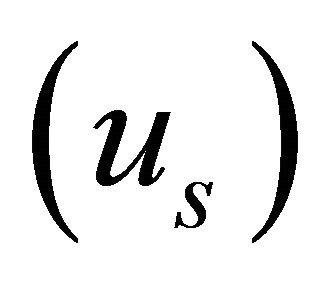 and radius of curvature from centerline of the channel
and radius of curvature from centerline of the channel 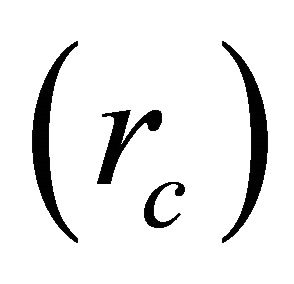 are related as;
are related as;
 (4)
(4)
[14] noted that;
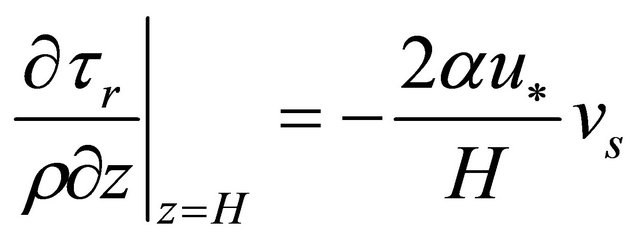 (5)
(5)
 (6)
(6)
Substituting (5) and (6) into (4), yields;
 (7)
(7)
[15] observed that;
 (8)
(8)
where m is the friction term in steady flow which is defined as;
 (9)
(9)
Substituting Equation (8) into (7) and since 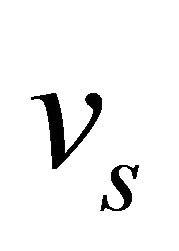 is a function of
is a function of  only, it yields;
only, it yields;
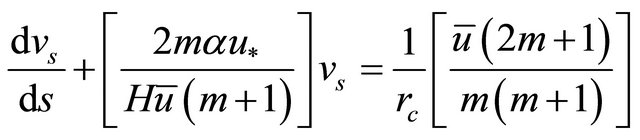 (10)
(10)
Since meander initiate in a river channel at a very large value of radius of curvature (r), the transverse slope according to Equation (6) is almost negligible and therefore the channel cross-section can be assumed to be rectangular when meander just forms in a river channel. The channel-alignment perturbation will be taken to be a migrating sinusoid as shown in Figure 3.
According to [16], the perturbation displacement from the convex bank to concave bank is given by;
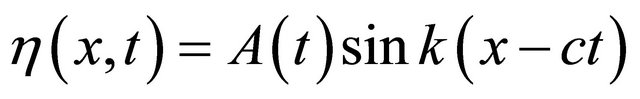 (11)
(11)
 (12)
(12)
[16] observed that;
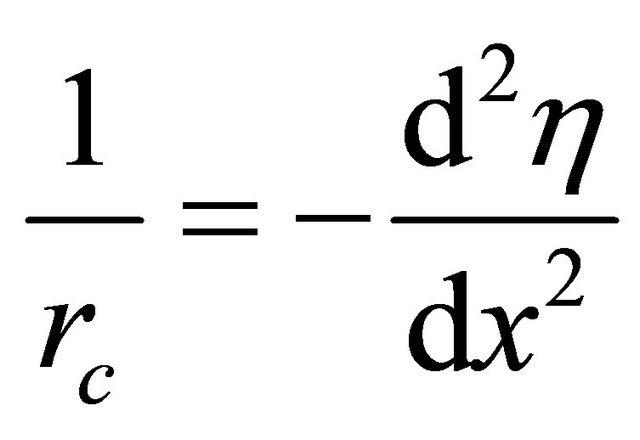 (13)
(13)
Substituting (11) into (13) yields;
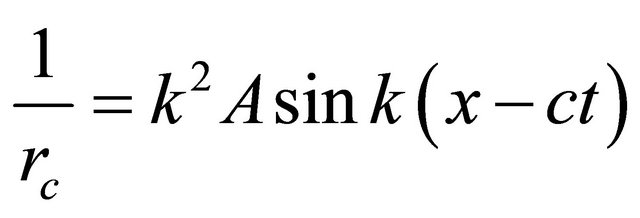 (14)
(14)
Substituting (14) into (10) yields;
 (15)
(15)
Equation (15) is linear ordinary differential equation. The solution of this equation that is periodic and independent of the initial condition is:
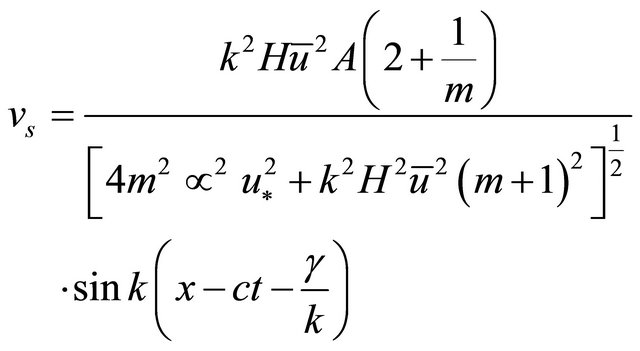 (16)
(16)
where
 (17)
(17)
The phase shift 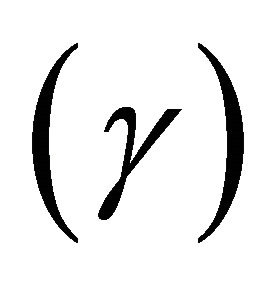 must vary between zero and pie because the primary flow is assumed to be stronger than the secondary current. The velocity of secondary current attains maximum when the phase shift is approximately equal to
must vary between zero and pie because the primary flow is assumed to be stronger than the secondary current. The velocity of secondary current attains maximum when the phase shift is approximately equal to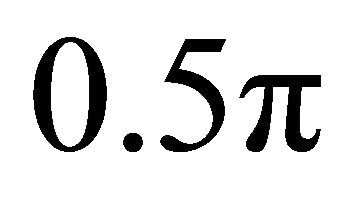 . This happens when the inertial term is dominant over the friction term. The velocity of secondary current is in phase with the channel axis displacement when the phase shift is approximately equal to zero. [16], argued that as the control volume moves laterally in a curved river channel, the difference between the rates of these processes at the concave and convex banks is given by;
. This happens when the inertial term is dominant over the friction term. The velocity of secondary current is in phase with the channel axis displacement when the phase shift is approximately equal to zero. [16], argued that as the control volume moves laterally in a curved river channel, the difference between the rates of these processes at the concave and convex banks is given by;
 (18)
(18)
Since the channel centerline is curved, the centroid of the central volume is not at mid width of the channel, but is displaced toward the concave bank, the displacement being inversely proportional to the radius of the curvature. [16] argued that for a rectangular channel crosssection, the displacement is . They obtained the rate of lateral migration as;
. They obtained the rate of lateral migration as;
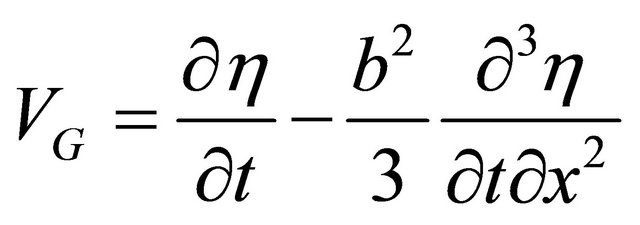 (19)
(19)
They also argued that the rate of differential erosiondeposition across the channel is proportional to the rate of a fictious lateral transport of sediment from the outer to the inner bank. Therefore;
 (20)
(20)
Substitution of (20) into (18) yields;
 (21)
(21)
Substitution of (21) into (19) yields;
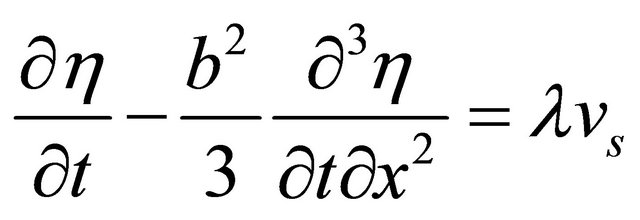 (22)
(22)
Substitution of (11) and (16) into (22) and simplifying yields:
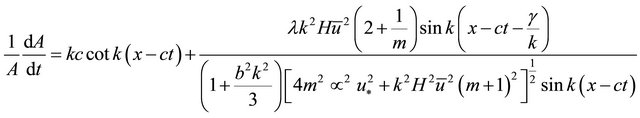 (23)
(23)
Integrating Equation (23) and simplifying it yields;
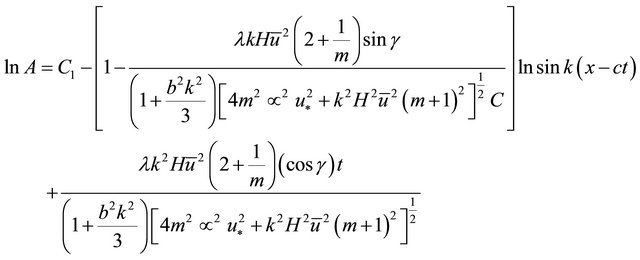 (24)
(24)
Equation (24) is satisfied if;
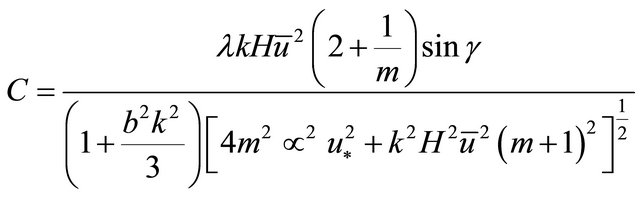 (25)
(25)
Therefore Equation (24) reduces to;
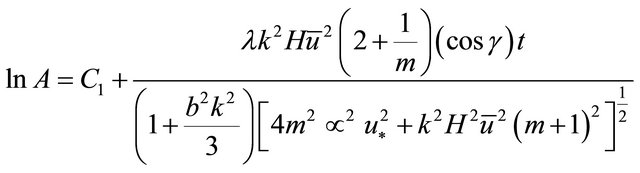 (26)
(26)
Since at  Equation (26) simplifies;
Equation (26) simplifies;
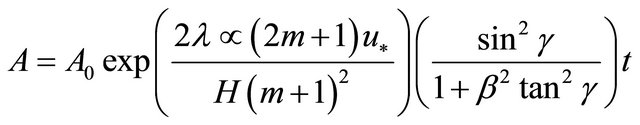 (27)
(27)
where
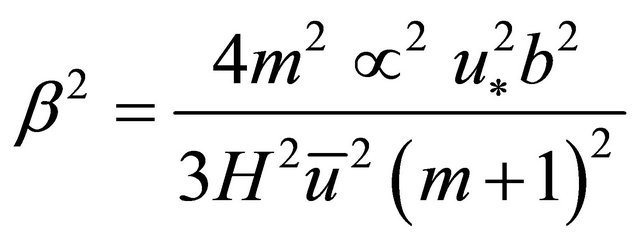 (28)
(28)
And
 (29)
(29)
Equation (27) therefore simplifies to (see Equation (30) below).
The exponent in Equation (30) is positive for all k. Therefore the amplitude of the sinusoidal perturbation increases exponentially with time.
 (30)
(30)
It is observed in Equation (30) that the exponent tends to zero again for k = ∞. However there is a dominant wave number for which the rate of growth is maximum. The dominant wave number for which the rate of growth is maximum is observed when . Substituting this in (28) and simplifying yields.
. Substituting this in (28) and simplifying yields.

where
 (31)
(31)
Substitution of (17) and (28) into (31) yields;
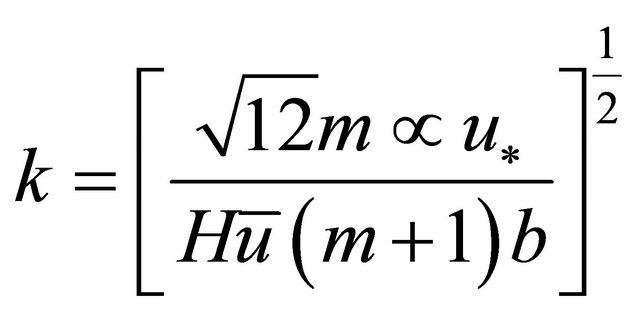 (32)
(32)
Equation (32) defines the dominant wave number. Substitution of (12) into (30) yields;
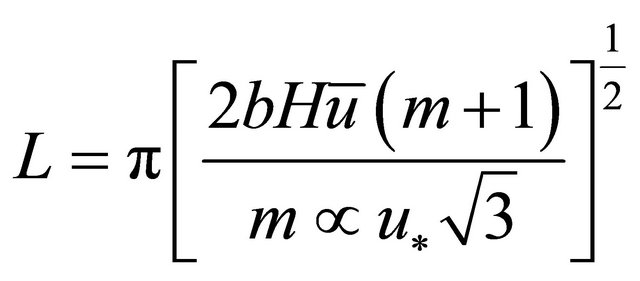 (33)
(33)
Substitution of (10) into (33) yields;
 (34)
(34)
where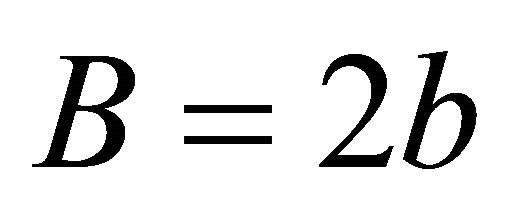 . Since
. Since 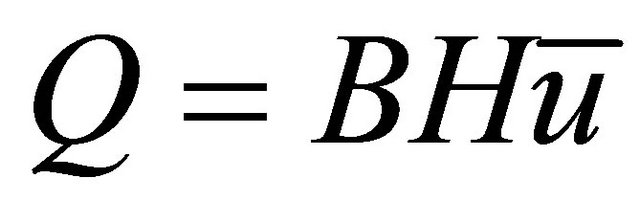 Equation (34) simplifies to;
Equation (34) simplifies to;
 (35)
(35)
Therefore the predicted/dominant meander wavelength as a function of dominant discharge is given by Equation (35). Substitution of (32) into (17) and then (8) yields;
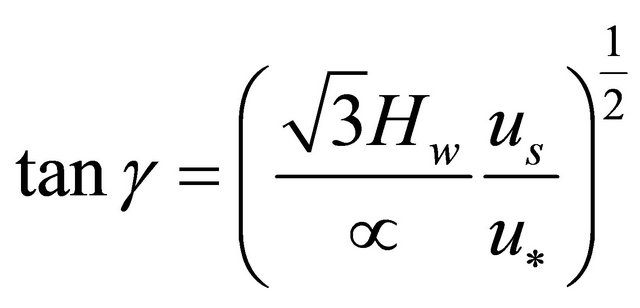 (36)
(36)
Making 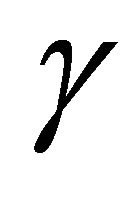 the subject in (36) yields;
the subject in (36) yields;

where,
 (37)
(37)
Substitution of (32), into (25) and after some algebraic manipulations yields;
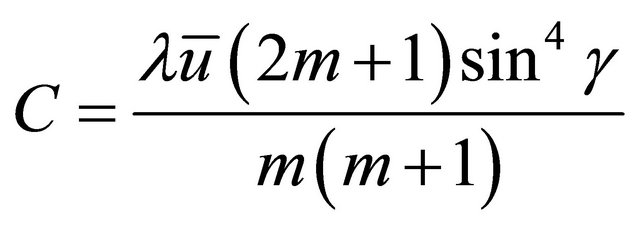 (38)
(38)
According to [13],  while [17] noted that
while [17] noted that 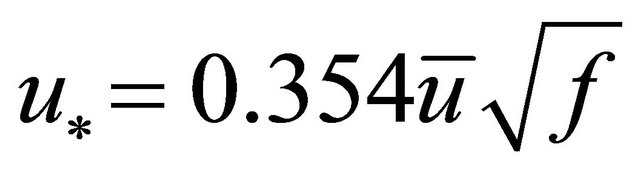 and therefore
and therefore . Substituting all this in Equation (38) yields.
. Substituting all this in Equation (38) yields.
 (39)
(39)
Equation (39) defines the migration velocity of the meander pattern which is also called the celerity (C).
Substitution of (32) into (30) and after some algebraic manipulations, equation of the amplitude of the dominant wave is obtained as follows;
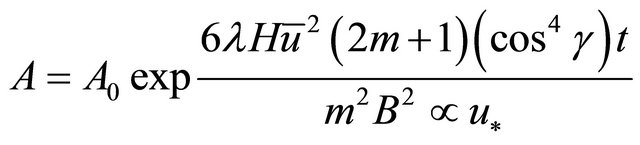 (40)
(40)
Since 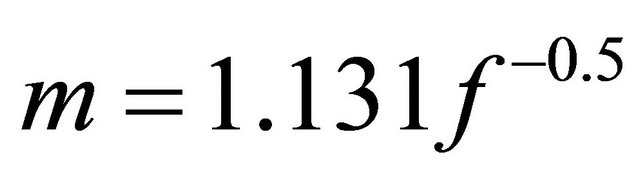 Equation (40) simplifies to;
Equation (40) simplifies to;

(41)
4. Results and Discussion
The foregoing analysis demonstrates that secondary currents produced by small periodic perturbations in the alignment of an otherwise straight channel can cause the amplitude of the perturbations to increase with time, and produce downstream migration of the resulting meanders. The stability analysis is linear and it’s therefore applicable only to small-amplitude meanders. It’s observed from Equation (34) that the predicted/dominant wavelength (L) at which meandering occurs is proportional to square root of the ratio of longitudinal surface velocity to bed shear velocity. This is the ratio at which meandering occurs and it therefore reduces as meandering process continues. This ratio can only be maximized if the shear velocity is minimized and longitudinal surface velocity is maximized. It is observed from Equations (39) and (41) that channel roughness increases as meandering process continues. This is in agreement with the existing theory since more alternate bars and ripples which causes an increase in roughness forms as meandering process occurs. Hence there is a need to determine the ratio of longitudinal surface velocity to shear velocity at which meandering occurs.
Several laboratory experiments have been conducted to determine the dominant wavelength (L). Based on Equation (34) the flume experimental results obtained by [18] were used to determine the above ratio. This was done by rearranging Equation (34) to get;
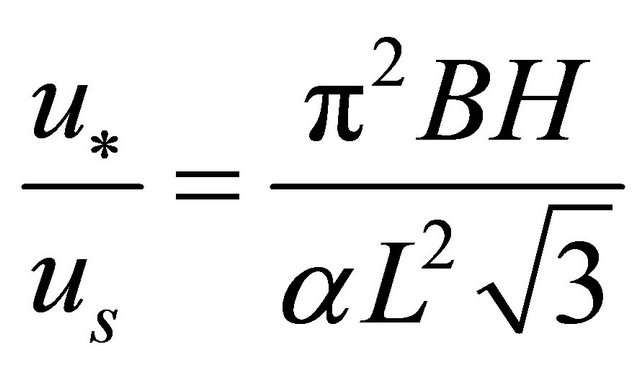 (42)
(42)
[18] presented a data from 167 laboratory flume experiments which were carried out by nine groups of researchers. To determine the ratio 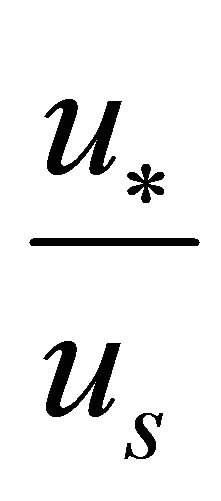 the results from the same flume type (S-E) were used to avoid errors that might arise by using results from different flume types. The mean value was found to be 0.01. Hence from experimental results it’s observed that the ratio at which meander forms in a river channel is approximately 0.01.
the results from the same flume type (S-E) were used to avoid errors that might arise by using results from different flume types. The mean value was found to be 0.01. Hence from experimental results it’s observed that the ratio at which meander forms in a river channel is approximately 0.01.
Hence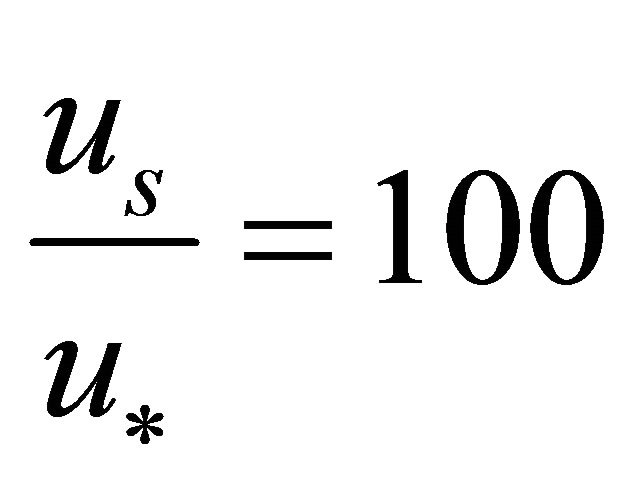 .
.
Substituting the above mean in Equation (36) and taking 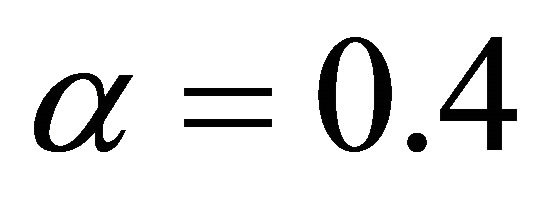 [19] yields;
[19] yields;
 (43)
(43)
Equation (43) gives the approximate predicted/dominant meander wavelength  obtained from experimental flume data.
obtained from experimental flume data.
Due to errors that occur in any experiment, simulations were carried out using MATLAB version nine to determine again the ratio of  at which meander forms in a river channel. Using Equation (34), Figures 4(a) and (b) were obtained for different values of channel breadth (B) and depth (H).
at which meander forms in a river channel. Using Equation (34), Figures 4(a) and (b) were obtained for different values of channel breadth (B) and depth (H).
It’s observed from Figures 4(a) and (b) that the channel remains straight beyond point B. From B to A, meandering takes place. From A to O, braiding is observed. Meandering therefore forms in a river channel at a maximum value of 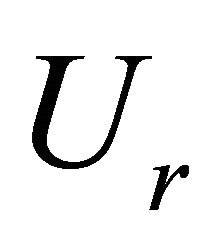 being 200 and the minimum value being 100. The average value of
being 200 and the minimum value being 100. The average value of 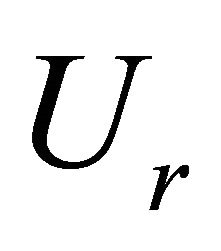 at which meandering forms is therefore 150. Therefore river channel will remain straight when
at which meandering forms is therefore 150. Therefore river channel will remain straight when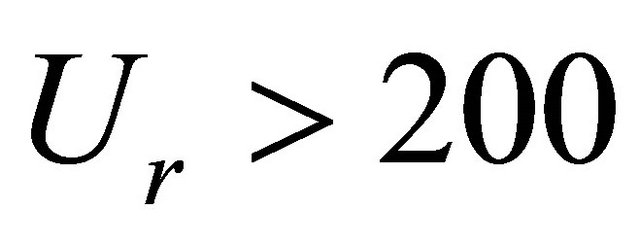 , transition from straight to meandering occurs when
, transition from straight to meandering occurs when , meandering occurs when
, meandering occurs when 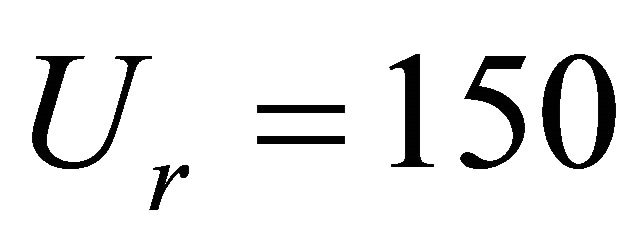 transition from meandering to braiding occurs when
transition from meandering to braiding occurs when  and braiding occurs when
and braiding occurs when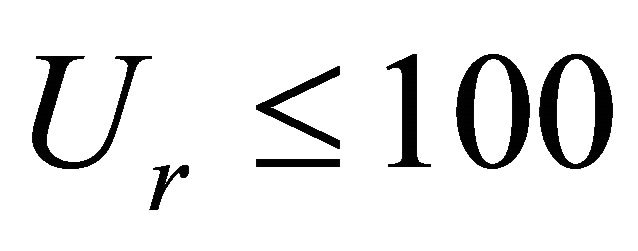 . Therefore as
. Therefore as  decreases, the channel pattern changes from straight to meandering and then from meandering to braiding. This is because of the fact that
decreases, the channel pattern changes from straight to meandering and then from meandering to braiding. This is because of the fact that 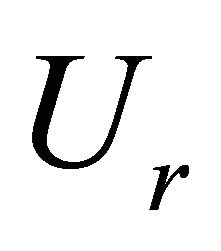 can only reduce when
can only reduce when  increases and according to [17] the friction factor will also increase. An increase in friction factor causes more
increases and according to [17] the friction factor will also increase. An increase in friction factor causes more

Ur
(a)

Ur
(b)
Figure 4. (a) Predicted wavelength (L) against the ratio of longitudinal surface velocity to shear velocity (Ur); B = 0.4917 and H = 0.00809; (b) Predicted wavelength (L) against the ratio of longitudinal surface velocity to shear velocity (Ur); B = 127.1 and H = 8.2.
resistance to the flow and hence deposition which leads to formation of bars that forms braiding.
The channel is expected to be straight when the phase shift is maximum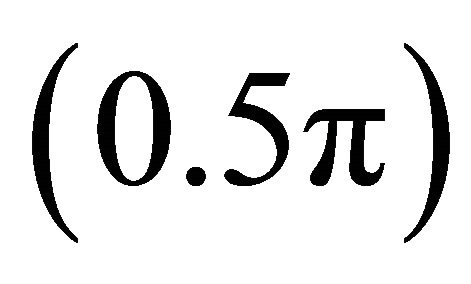 . This happens when the inertial term is dominant over the friction term and the secondary current is said to have the maximum velocity near the channel axis. The secondary current is nearly in phase with the channel axis displacement if the phase shift is approximately equal to zero. Therefore meandering process is expected to start in a river channel when phase shift angle decreases from
. This happens when the inertial term is dominant over the friction term and the secondary current is said to have the maximum velocity near the channel axis. The secondary current is nearly in phase with the channel axis displacement if the phase shift is approximately equal to zero. Therefore meandering process is expected to start in a river channel when phase shift angle decreases from 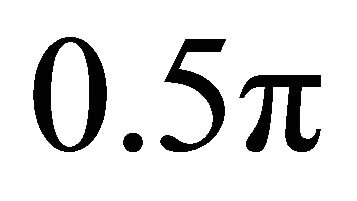 towards zero. This is why downstream migration is dominant when meandering starts in a river channel. As phase shift reduces towards zero, meander growth is dominant.
towards zero. This is why downstream migration is dominant when meandering starts in a river channel. As phase shift reduces towards zero, meander growth is dominant.
Based on Equation (37) simulations were done using MATLAB version nine to determine the value of the phase shift at which meandering occurs.
Comparing the results shown in Figure 5 and the above argument given by [10], it’s noted that; braiding occurs when 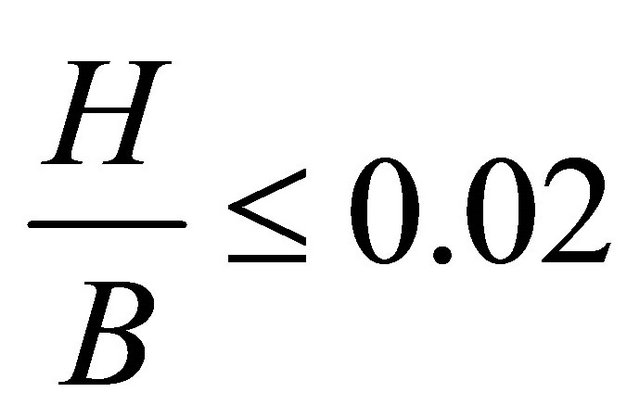 , meander-braid transition falls in the region
, meander-braid transition falls in the region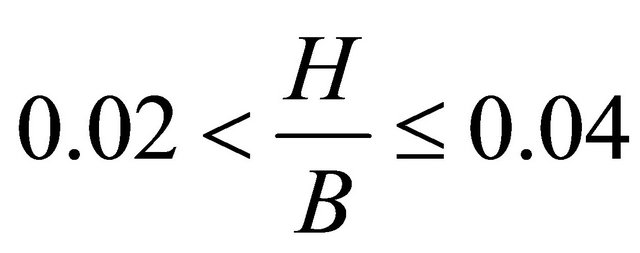 , meandering develops when
, meandering develops when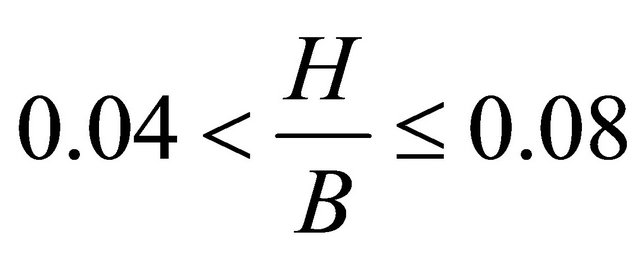 , straight to meander transition falls in the region
, straight to meander transition falls in the region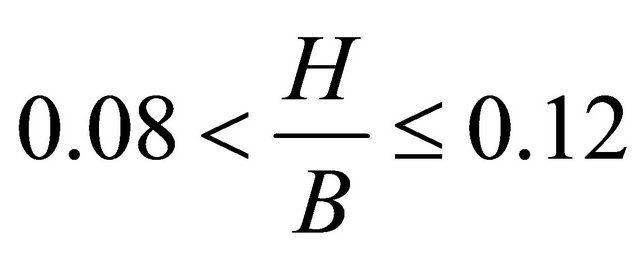 , channels remain straight when
, channels remain straight when .
.
It’s therefore observed from Figure 5 that: 1) OA represents braiding; 2) AB represents transition from meandering to braiding; 3) BC represents meandering; 4) CD represents transition from straight to meandering and beyond D represents straight channel. Using Equation (37), values of  obtained from Figures 4(a) and (b), values of
obtained from Figures 4(a) and (b), values of  obtained from Figure 5 and using Figure 1, it’s observed that the river is stable when
obtained from Figure 5 and using Figure 1, it’s observed that the river is stable when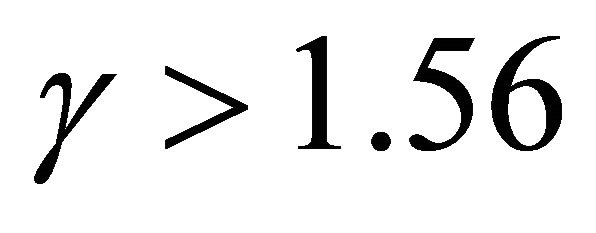 , moderately stable when
, moderately stable when , moderately unstable when
, moderately unstable when , unstable when
, unstable when 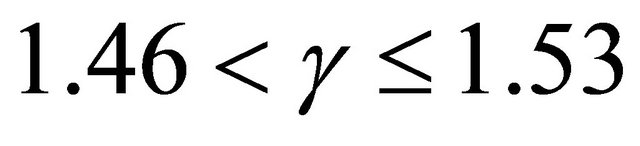 and highly unstable when
and highly unstable when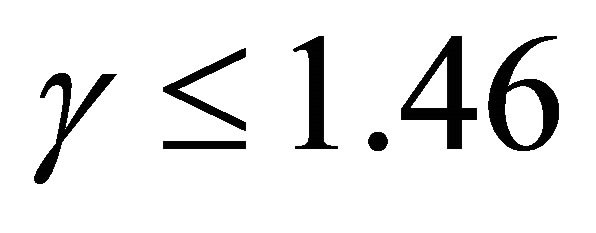 . It’s also noted that the river remains straight when
. It’s also noted that the river remains straight when , transition from straight to meandering occurs when
, transition from straight to meandering occurs when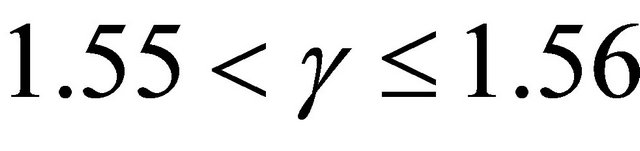 , meandering occurs when
, meandering occurs when , transition from meandering to braiding occurs when
, transition from meandering to braiding occurs when  and braiding occurs when
and braiding occurs when . Therefore river changes from straight to meandering and then from meandering to braiding as the phase shift angle reduces. This is because of the fact that the resistance that the secondary current causes on the primary flow increases with decrease in phase shift angle and hence causing more deposition which leads to braiding.
. Therefore river changes from straight to meandering and then from meandering to braiding as the phase shift angle reduces. This is because of the fact that the resistance that the secondary current causes on the primary flow increases with decrease in phase shift angle and hence causing more deposition which leads to braiding.
Therefore the dominant/predicted meander wavelength occurs when phase shift ranges between 1.53 to 1.55.

Hw
Figure 5. Phase shift against the aspect ratio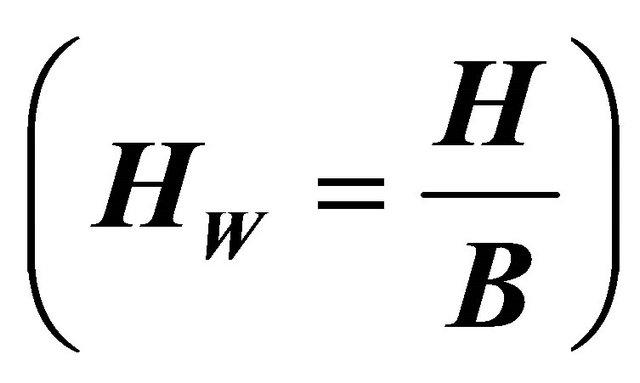 .
.
Therefore the predicted phase shift ranges between 1.53 to 1.55. This is in agreement with [16] findings who noted that the predicted phase shift should be greater than 0.786. According to [20,21] such large phase shift indicates that the frictional torque is generally smaller than the torsional inertia and is also associated with strong tendency of the meanders to migrate downstream incase of weakly meandering channels. [22] argued that flows on strongly curved channels indicate small phase shifts and pronounced rates of meander growth as compared with migration velocities.
5. Conclusion
The phase shift between the secondary current and the channel axis displacement were calculated and used to distinguish between braiding, meandering and straight patterns of the river channel. It’s observed that river channel changes from straight to meandering and then from meandering to braiding as the phase shift angle reduces. This is because of the fact that the resistance that the secondary current causes on the primary flow increases with decrease in phase shift angle and hence causing more deposition which leads to braiding. Instability was observed to increase with decrease in phase shift angle. This is due to the fact that secondary currents are more directed on the river banks and hence causing more erosion on the concave bank and more deposition on the convex bank at small phase shift angle. Meander growth dominates downstream meander migration at small phase shift angle and vice versa. It was also noted that channel changes from straight to meandering and then from meandering to braiding takes place as the ratio of longitudinal surface velocity to bottom shear velocity reduces. This is due to the fact that the reduction in the ratio is caused by an increase in bottom shear velocity which implies that there’s an increase in channel roughness. Increase in channel roughness causes an increase in resistance to the flow and hence causing more deposition to take place which leads to the formation of bars that result to braiding. According to this research meander is initiated in a river channel when secondary flow is generated. Therefore any factor that triggers the formation of secondary currents will have a major contribution in interfering with the stability of a river channel. Some of these factors are: i) change in slope; ii) change in channel width; and iii) formation of ripples among others. It’s therefore noted that phase shift angle and the ratio of longitudinal surface velocity to bottom shear velocity play a major role in determining the stability and the pattern of a river channel. The theory developed has provided a hydrodynamic explanation of meandering process.
Nomenclature
b: Channel half-width F: Froude number f: Darch-Weisbach friction factor H: Average water depth HW: Depth-width ratio k: Wave number L: Meander wavelength n: Manning’s roughness coefficient Q: Discharge Qd: Dominant discharge Ql: Lateral discharge R: Hydraulic radius
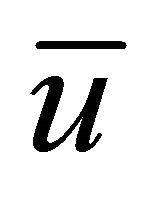 : Depth-averaged longitudinal velocity
: Depth-averaged longitudinal velocity
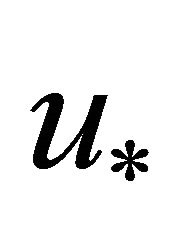 : Shear velocity at the bottom
: Shear velocity at the bottom
α: Von Karman constant
 : Positive dimensionless constant
: Positive dimensionless constant
 : Local displacement of Control volume of length ds.
: Local displacement of Control volume of length ds.
x: Coordinate distance along the unperturbed channel axis
NOTES