1. Introduction
The Pacific shrimp fishery is the most important fishery of Mexico in terms of catch levels, economic value, and number of people involved. This is a multispecies resource which displays an important spatial and temporal-dynamic, high reproductive potential, and a relatively short life cycle of less than two years. The Pacific Ocean provides 78% of shrimp harvested in Mexico and the southeastern Gulf of California supports the main part of this fishery [1,2], particularly in coastal Sinaloa and Nayarit, with a large number of coastal lagoons and excellent trawling areas along the continental shelf (Figure 1). The main species supporting this fishery are the brown shrimp Farfantepenaeus californiensis, blue shrimp Litopenaeus stylirostris, and white shrimp Litopenaeus vannamei with 96% of the catch in this region for all three

Figure 1. The study area in the Gulf of California. Trawl area by the Sinaloa fleet lies within the dotted line with arrows.
species. The most abundant species in the fishery by weight is brown shrimp.
An overcapitalization of the fishery has been recognized, caused mainly by overfishing of blue and white shrimp [3,4]. However, the Secretariat of Agriculture, Livestock, Rural Development, Fisheries and Food, SAGARPA, considers that the brown shrimp fishery in the states of Sinaloa and Nayarit is at its maximum sustainable yield [5].
For species such as penaeids with short life spans, where the annual catch depends almost entirely upon one-year recruits during the fishing period, analysis of interannual variation in abundance and the development of plausible models are essential for the rational exploitation of the resource. Commonly, catch and effort data are analyzed using biomass dynamic models. These models are an alternative to age-structured estimation approaches, such as virtual population analysis, when the information on age structure of the catch is not available. Biomass dynamic models are the most commonly used stock assessment techniques for shrimp, and have become a powerful analysis tool [6-11].
When models are used to ascertain the dynamic behavior of a fishing system, it is important to assess their possible sources of error. Deviations of predicted values can be assumed to be normally distributed around a mean value, hence large deviations from the mean are considered less likely than small ones.
In this work we analyzed the brown shrimp fishery of Sinaloa in the southeastern Gulf of California using a dynamic biomass model, considering error structure in the model. Temporal variation in brown shrimp biomass was analyzed assuming two sources of variation, observation and process error. In addition, the magnitude and frequency of the perturbations away from the expected annual biomass values were also analyzed [7,12,13]. We attempt to explain changes in the abundance of brown shrimp through the parameters in the biomass dynamic model. According to reports which indicate that catch brown shrimp is the most abundant species, we expected that populations of this species has: a large carrying capacity, greater than the maximum recorded catch of 16,000 tons in 2006-07 season; a fast population growth with intrinsic growth rate values between one and two; and a low estimate of initial biomass, considering that catch in the first fishing season analyzed in this study was relatively low. Results presented can contribute to knowledge of the natural history of this species, which is used as an important fishery resource.
2. Material and Methods
The main brown shrimp fishing grounds are on the continental shelf of the states of Sinaloa and Nayarit. Annual catch (tones) and fishing effort (number of trips) of the Mazatlan trawl fleet from the fishing seasons (spanning from September to May) 1995-96 to 2010-11 were obtained from official records (Figure 2).
Model
We used the stochastic version of the biomass dynamic Schaefer model [14]. This model does not assume equilibrium conditions, and it represents an advantage to stock assessment of species with short life spans, such as the brown shrimp. In this work we consider two sources of error: process and observation error. The model expression is:
 (1)
(1)
where  is time (fishing season);
is time (fishing season); 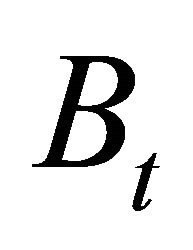 is biomass of the population vulnerable to fishing at time
is biomass of the population vulnerable to fishing at time ;
;  is the population intrinsic growth rate;
is the population intrinsic growth rate;  the carrying capacity;
the carrying capacity;  the catch at time
the catch at time ; and
; and 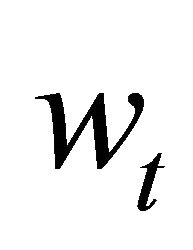 is the process error assuming a log-normal distribution. Process error assumes that the variability in the state of the population is produced by natural factors not included in the model, such as environmental forcing.
is the process error assuming a log-normal distribution. Process error assumes that the variability in the state of the population is produced by natural factors not included in the model, such as environmental forcing. 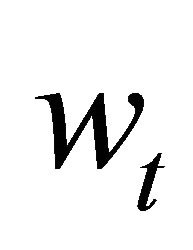 was estimated as:
was estimated as:  [15].
[15].
CPUE was used as an index for abundance at time . It is generally assumed that
. It is generally assumed that  is proportional to biomass:
is proportional to biomass:
 (2)
(2)
where  is the catchability; and
is the catchability; and  is the observation error assuming a log-normal distribution. Observation errors can arise when applying sampling techniques to variables of interest and can be attributed to erroneous human observations or sampling devices. In the model we assumed that the index
is the observation error assuming a log-normal distribution. Observation errors can arise when applying sampling techniques to variables of interest and can be attributed to erroneous human observations or sampling devices. In the model we assumed that the index  was measured with error. Therefore, the variability in the population was caused by uncertainty of the true value of the index
was measured with error. Therefore, the variability in the population was caused by uncertainty of the true value of the index 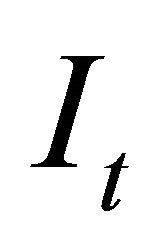 [16].
[16].  was estimated as:
was estimated as: , and q was comput-
, and q was comput-

Figure 2. Catch (solid line) and effort (dotted line) reports by season for brown shrimp (Farfantepenaeus californiensis) in the southeastern Gulf of California, Mexico.
ed using the following analytical solution only for the observation error estimator because there is no closed form solution for the estimate of 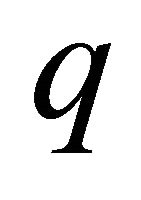 in process error estimator [17]:
in process error estimator [17]:
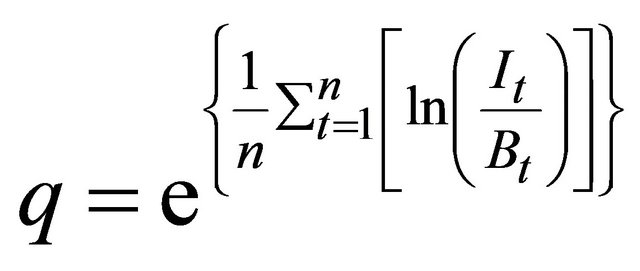 (3)
(3)
The estimation of the parameters given the index , was done by maximizing the following log likelihood
, was done by maximizing the following log likelihood  function [6]:
function [6]:
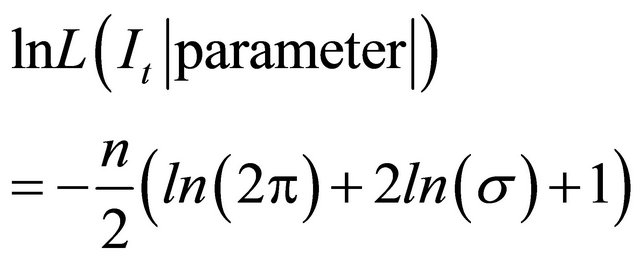 (4)
(4)
where  is the log likelihood,
is the log likelihood,  is the data number (
is the data number ( for the process error estimator); and
for the process error estimator); and  is the standard deviation of the error, estimated using the following equation:
is the standard deviation of the error, estimated using the following equation:
 (5)
(5)
We estimated the parameters ,
,  and
and  (initial biomass) for the observation error estimator (subscript
(initial biomass) for the observation error estimator (subscript 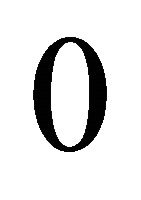 is the observation error), and parameters
is the observation error), and parameters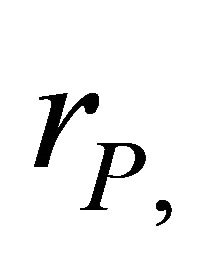 ,
,  and
and , for the process error estimator (subscript P refers to the process error).
, for the process error estimator (subscript P refers to the process error).
We used σ,  and Akaike information criterion (
and Akaike information criterion (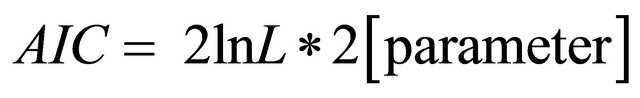 ) to determine which of both models best fit the data. The following quantities of relevance for management were computed: the maximum sustainable yield
) to determine which of both models best fit the data. The following quantities of relevance for management were computed: the maximum sustainable yield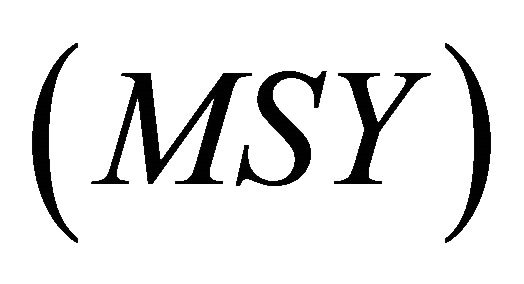 ; effort at which
; effort at which  will be achieved
will be achieved ; and biomass at which
; and biomass at which 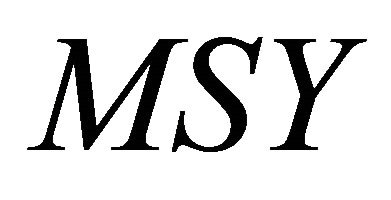 will be achieved
will be achieved . We also computed a prediction of catch
. We also computed a prediction of catch  in the following season (2011/12) using the average effort of time-series observed of 2474 trips (Table 1).
in the following season (2011/12) using the average effort of time-series observed of 2474 trips (Table 1).
In order to assess the precision of the key parameter estimates and quantities of relevance for management, confidence intervals and coefficients of variation were calculated using bootstrapping [6]. One-thousand random samples were produced from the original best-fit residual, with replacement, to generate a new vector of bootstrapped residuals. This vector of bootstrapped residuals was combined with the optimum vector of expected  data to obtain each new bootstrap sample of
data to obtain each new bootstrap sample of  data [18]. In this way a new time-series of boot
data [18]. In this way a new time-series of boot
Table 1. Models for management quantities.

strapped observed  data were generated to which the model was refitted and the parameters re-estimated. Bootstrap confidence intervals (95%) were estimated using the 0.025 and 0.975 percentiles values.
data were generated to which the model was refitted and the parameters re-estimated. Bootstrap confidence intervals (95%) were estimated using the 0.025 and 0.975 percentiles values.
3. Results
3.1. Model Fitting
Parameters values fitted to the biomass dynamic Schaefer model assessing the stock of brown shrimp in the southeastern Gulf of California are given in Figure 3. Three different measures of fit ( ,
,  , and
, and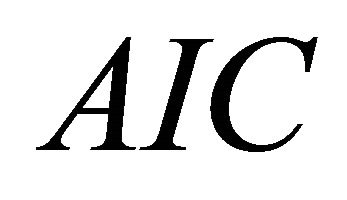 ) indicated that observation error resulted in a better fit than the process error (Table 2). Estimated
) indicated that observation error resulted in a better fit than the process error (Table 2). Estimated  considering observation error better fit the data, showing less uncertainty in the estimate of the parameters.
considering observation error better fit the data, showing less uncertainty in the estimate of the parameters.
Except for the first fishing seasons, estimated  was similar using both models. The process error estimator suggests a high
was similar using both models. The process error estimator suggests a high  in season 1997-98 when observed
in season 1997-98 when observed  is low; whereas the observation error estimator yielded a low
is low; whereas the observation error estimator yielded a low  for season 1996-97, when the
for season 1996-97, when the  observed is high (Figure 4). Major discrepancies were observed between biomass estimates using the alternative modeling approaches. Biomass estimates using both models suggest different stories. Consideration of observation error suggests that biomass has been growing over time, while the model with process error suggests quite the opposite (Figure 5).
observed is high (Figure 4). Major discrepancies were observed between biomass estimates using the alternative modeling approaches. Biomass estimates using both models suggest different stories. Consideration of observation error suggests that biomass has been growing over time, while the model with process error suggests quite the opposite (Figure 5).
3.2. Parameter Precision
Bootstrap results shown in Table 3 indicate that the parameters in the observation error estimator were consistent. Parameters 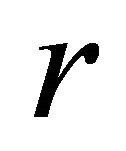 and
and , however, were somewhat skewed in the case of the process error. A point estimated values of r and
, however, were somewhat skewed in the case of the process error. A point estimated values of r and  were, respectively, 1.32 and 25,350 t; corresponding median bootstrap values were 1.59 and 19,520 t. The
were, respectively, 1.32 and 25,350 t; corresponding median bootstrap values were 1.59 and 19,520 t. The  parameter estimates were very close to their median values for both models, but more precisely estimated by the process error estimator.
parameter estimates were very close to their median values for both models, but more precisely estimated by the process error estimator.
3.3. Management Quantities
The estimated  were similar, with median bootstrap values of 9040 tones and 10,680 tones considering observation and process error, respectively; the coefficient of variation in the case of observation error was
were similar, with median bootstrap values of 9040 tones and 10,680 tones considering observation and process error, respectively; the coefficient of variation in the case of observation error was
Table 2. Three measures of fit of the observation error and process error model to data.

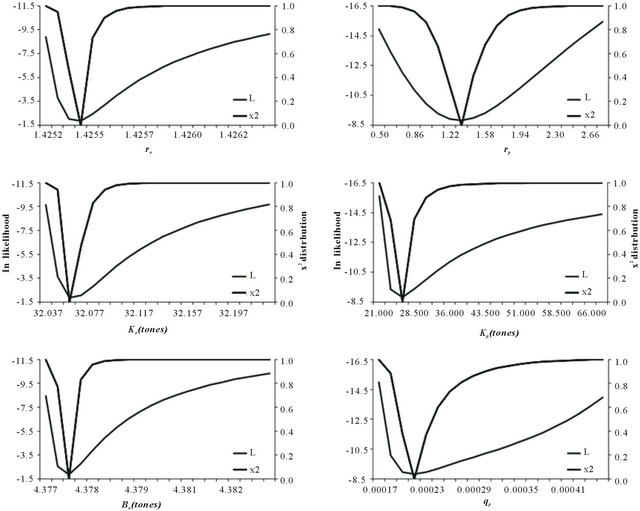
Figure 3. The likelihood profile and x2 distribution for the estimation parameter. On the left the estimation parameters for the observation error and on the right side the parameters estimated with process error. The subscript o and p is for observation and process error respectively.

Figure 4. Estimation of CPUE considering observation error (solid line) and process error (dotted line). The dots show the observed CPUE.
smaller than when considering process error. The 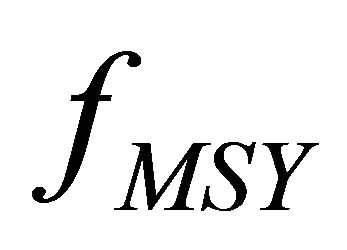 were considerably different for both models, with a 3:1 ratio in process error and observation error estimators, respectively. The
were considerably different for both models, with a 3:1 ratio in process error and observation error estimators, respectively. The  with process error estimator was lower than
with process error estimator was lower than  with the same model, which would indicate a poor fit of the model.
with the same model, which would indicate a poor fit of the model.
Finally, the predicted catch for the 2011-12 fishing season was similar using both models, with a median bootstrap value of 9630 tones and 8470 tones for obser,

Figure 5. Biomass estimates and confidence intervals computed with observation error (solid lines) and process error (dotted lines).
vation error and process error, respectively; however, coefficients of variation in both models were high. In general, coefficients of variation when assuming observation error were lower than assuming process error.
Bootstrap results for  considering observation error resulted in an overall good fit to data (Figure 6). The confidence intervals include a substantial number of observed data; however, the model underestimated
considering observation error resulted in an overall good fit to data (Figure 6). The confidence intervals include a substantial number of observed data; however, the model underestimated 
Table 3. Bootstrap results, confidence range and coefficients of variation (CV) of the parameter values and quantities for management of brown shrimp from the Gulf of California, Mexico.

Figure 6. Estimation of CPUE with observation error (solid line) and 95% bootstrap confidence intervals (dotted line) by bootstrapping. The dots are the observed CPUE.
in seasons 1996-1997 and 2006-2007, and overestimated  in season 2000-2001.
in season 2000-2001.
4. Discussion
It is important to constantly update the information and assess the status of the Pacific brown shrimp population. We may do this using a heuristic approach to evaluate the health of the population, its exploitation status, and appropriate catch levels using biomass models. When doing so one must bear in mind the potential sources of error and the implications for management recommendations.
4.1. Bootstrapping and Model Fitting
A better measure of fishing effort in industrial shrimp fisheries might be trawl time or trip days; however, in the brown shrimp fishery of the southeastern Gulf of California, this information was not available. The data used in this work comes from the reports provided by skippers of the shrimp boats of Sinaloa. Shrimp fishing trips by vessels in the study area average 30 days and must often travel long distances without fishing, which represents a real difficulty to record the number of fishing days. Here we used the number of trips and considered it a good measure of fishing effort in terms of its statistical validity and the simplicity for obtaining it [19-21].
To interpret the annual change observed in catch, which is related to biomass availability, of brown shrimp two sources of error were investigated. The trend in  considering observation error showed a better fit to observed data than when consideration process error [8,16,18,22]. In the case of brown shrimp, with a lifespan of less than two years and subject to a fishery that each year takes a significant proportion of the biomass, the use of state-space Bayesian models might outperform likelihood model approaches including estimators of observation and process errors [10]. Our results are robust and sufficient for our present purposes and can be used as starting points for future research [8].
considering observation error showed a better fit to observed data than when consideration process error [8,16,18,22]. In the case of brown shrimp, with a lifespan of less than two years and subject to a fishery that each year takes a significant proportion of the biomass, the use of state-space Bayesian models might outperform likelihood model approaches including estimators of observation and process errors [10]. Our results are robust and sufficient for our present purposes and can be used as starting points for future research [8].
Acceptance of the hypothesis of observation error assumes that fluctuations in  are caused by uncertainty in the true value of the index of abundance [15,17]. This study provides the option of formulating new fisheries hypotheses, for example, using models that incorporate fisheries-independent information as abundance indices.
are caused by uncertainty in the true value of the index of abundance [15,17]. This study provides the option of formulating new fisheries hypotheses, for example, using models that incorporate fisheries-independent information as abundance indices.
A key challenge for future studies is our current inability to discriminate fishing effort by species. Effort is reported for all species of the shrimp fishery and this could create uncertainty when estimating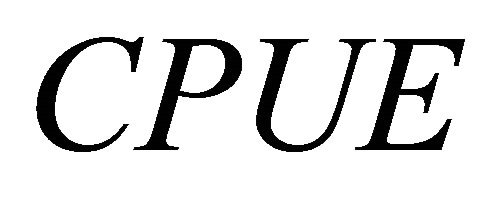 . Another source of error could be the changing fishing power (“effort creep”). This problem is common in stock assessment using biomass dynamic models because a key assumption is that the relationship between catch rate and stock biomass is linear and remains constant through time. Several authors suggest that
. Another source of error could be the changing fishing power (“effort creep”). This problem is common in stock assessment using biomass dynamic models because a key assumption is that the relationship between catch rate and stock biomass is linear and remains constant through time. Several authors suggest that  may increase as fishermen become more knowledgeable about the resource and how to exploit it, or due to improvements in fishing gear [6,23-27]. Another bias could be the underreported catch.
may increase as fishermen become more knowledgeable about the resource and how to exploit it, or due to improvements in fishing gear [6,23-27]. Another bias could be the underreported catch.
The fits of parameters r and  with both models were similar; however, the uncertainty showed with the process error was greater. Under observation error,
with both models were similar; however, the uncertainty showed with the process error was greater. Under observation error, 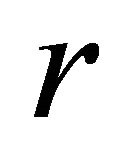 variedfrom 1.32 to 1.42 (bootstrapped values). For shortlived species such as brown shrimp, the value of parameter
variedfrom 1.32 to 1.42 (bootstrapped values). For shortlived species such as brown shrimp, the value of parameter  approaches 1.0 [16]. Morales-Bojorquez et al. [7] estimated
approaches 1.0 [16]. Morales-Bojorquez et al. [7] estimated  values of 2.50 for the same species with observation error, and 4.06 with process error; MadridVera et al. [11] estimated values of 0.34 for Litopenaeus vannamei using observation error; and García-Juárez et al. [28] estimated values of 1.18 for Litopenaeus styilirostris using observation error. Thus our best estimate for this parameter is well within the expected value for the species, and below a value which will theoretically generate deterministic chaos in population trajectories, a situation which is not supported by observations [6]. Bootstrap results always indicated that the parameters
values of 2.50 for the same species with observation error, and 4.06 with process error; MadridVera et al. [11] estimated values of 0.34 for Litopenaeus vannamei using observation error; and García-Juárez et al. [28] estimated values of 1.18 for Litopenaeus styilirostris using observation error. Thus our best estimate for this parameter is well within the expected value for the species, and below a value which will theoretically generate deterministic chaos in population trajectories, a situation which is not supported by observations [6]. Bootstrap results always indicated that the parameters 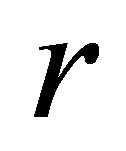 and K with process error were somewhat skewed, where the point estimate was different to median bootstrap value [8].
and K with process error were somewhat skewed, where the point estimate was different to median bootstrap value [8].
4.2. Status of Brown Shrimp
The trawl fishery for this species has exhibited fluctuations in total catch, from 3400 tons during 1998/99 to 15,000 tons during 2006/07. The average is 6900 tons per fishing season; only 75% of the  estimated median bootstrap value with observation error. Overfishing results if we considered season 2000/01 with 3,383 trips. Similarly, if we assess the state of the fisheries according to the largest catch in history, and we assume that the capture of the 2006/07 season is the highest, the fishery is also overfished [29].
estimated median bootstrap value with observation error. Overfishing results if we considered season 2000/01 with 3,383 trips. Similarly, if we assess the state of the fisheries according to the largest catch in history, and we assume that the capture of the 2006/07 season is the highest, the fishery is also overfished [29].
However, the catch has shown recovery in recent years. We found two fishing seasons with catches above the estimated ; 2006-07 with a catch of 15,183 tons and 2010-11 with a catch of 9050 tons. This improvement in catches could be due to recent management regulations introduced in the fishery, including reduction of number of vessels, in addition to temporal and spatial closures, both of which are having positive results in the fishery [2]. The mean fishing effort observed was of 2474 trips per season; this is larger than the
; 2006-07 with a catch of 15,183 tons and 2010-11 with a catch of 9050 tons. This improvement in catches could be due to recent management regulations introduced in the fishery, including reduction of number of vessels, in addition to temporal and spatial closures, both of which are having positive results in the fishery [2]. The mean fishing effort observed was of 2474 trips per season; this is larger than the  estimated with bootstrap value and under observation error (1710 to 2010 trips). Thus, ideally fishing effort needs be to decrease by 20% of the observed mean.
estimated with bootstrap value and under observation error (1710 to 2010 trips). Thus, ideally fishing effort needs be to decrease by 20% of the observed mean.
The  can be interpreted as the theoretical long term yield expected from the stock when it is at a fixed optimum fishing effort and optimum catch size. The last fishing season analyzed herein (2010-11) when an effort
can be interpreted as the theoretical long term yield expected from the stock when it is at a fixed optimum fishing effort and optimum catch size. The last fishing season analyzed herein (2010-11) when an effort  (2048 fishing trips) was applied and
(2048 fishing trips) was applied and  was achieved (9050 tones), gives hope that brown shrimp population may have a fast recovery, a response to management as expected for short-lived species.
was achieved (9050 tones), gives hope that brown shrimp population may have a fast recovery, a response to management as expected for short-lived species.
Variation in catch depends not only on fishing effort. There are sufficient indications that annual shrimp production may be varying in relation to environmental forcing [30-33]. But the mechanisms are complex and involve several factors, such as fecundity, recruitment, growth and survival [34,35], which are difficult to assess with the information used in this work.
4.3. Concluding Remarks
The recovery of the brown shrimp population is encouraging for fisheries management and ecosystem health in the region. Management tools such as the historical closed season, in addition to sustained reduced fleet size, catch quota, protection of shallow marine waters as nofishing zone, are promising areas for further discussion, implementation, updating and strengthening. We caution that the perceived exploitation level presented in this study should be further validated. On the other hand, consideration of observation error stresses the importance of accurate data sampling when using a dynamic Schaefer model [14] for the biomass estimates of Farfantepenaeus californiensis in the southeastern Gulf of California. Therefore, current sampling program to collect data should be continued and improved.
5. Acknowledgements
We thank the Centro Regional de Investigación Pesquera (CRIP) Mazatlan for support in obtaining data on brown shrimp. Thanks are due also to Juan Melchor Aragón for technical support. The first author thanks CONACYT for a doctoral scholarship. We also thank Alberto Rodriguez (PCMyL, UNAM) for help and useful contributions. Finally, we thank anonymous reviewers and editorial comments for their very useful suggestions to improve this manuscript.
NOTES