Study of Decoherence on the Teleportation Algorithm in a Chain of Three Nuclear Spins System ()
1. Introduction
It is well known now that in the real world the interaction of the system with the environment is almost unavoidable. The study of this type of systems implies a many bodies problem which is unsolvable within any picture of the quantum mechanics. At this moment, there are two approaches to attack this type of problems. The first one consists on to look for the phenomenological classical dissipative system and to get its associated Hamiltonian, then to proceed to do the usual quantization of the system [1] as an unitary evolution of the phenomenological system. The other one, which it is more fundamental, uses the matrix density approach for the whole system and makes the trace over the environment variables [2-8], the resulting density matrix is called “reduced density matrix”, and its associated non-unitary evolution equation is called “master equation”. In this sense, this equation is also phenomenological one, and it has defined a dissipative and diffusion parameters which can (non Markovian process) or can not (Markovian process) depend on the time evolution of the system. These parameter are responsible for the decay behavior of the non diagonal matrix elements of the reduced density matrix. This phenomenon is called “decoherence” because is related also with the disappearance of the interference terms of the product of the quantum wave function [9]. Decoherence is one of the mayor set back to build a full quantum computer of many qubits for real serious computation calculations (one would required of at least 1000 qubits) [10], and one of the most important phenomenon to be considered in quantum information [11]. The main mechanism to transport information between two quantum elements is the so called teleportation phenomenon [12]. Teleportation is a quantum procedure which is used to send a quantum state from the sender (Alice) to some receiver (Bob), and has already been used experimentally [13]. The study of decoherence is important here to determine how good this information is transferred (the fidelity must remain close to one). In this paper, we study the decoherence of the teleportation phenomenon in a chain of three nuclear spin one half [14], and for this propose, we will use approaches for quantum discrete system described in [15], which is based mainly in [7] and [16] approaches, and it was used for studying sudden death of entanglement of two qubits.
In the first part of our work, we describe the model and the Hamiltonian of our quantum system, and we must point out that, although this Hamiltonian will be time explicitly dependent, if we consider weak interaction between our system and the environment (the characteristic times of the quantum system are much longer than those of the environment) as a first approximation, the above mentioned Markovian-Lindblad master type equation can be still used for our study [11,17,18]. One needs to mention that even this linear chain of three nuclear spins model for solid state quantum computer has not been built yet, it has been very useful for theoretical studies about implementation of quantum gates and quantum algorithms [19-21] which can be extrapolated to other solid state quantum computers [22,23]. After doing this, we establish the five cases to be considered with the quantum-environment system: independent environment interaction (A), pure dephasing interaction (B), correlated dissipation interaction (C), dephasing correlated interaction (D), and thermalization case (E). The analyticcal dynamical systems of the reduced density matrix elements are obtained for these cases, and the results of the numerical simulations are presented. Finally, we study the behavior of the purity parameter for the teleportation algorithm.
2. Hamiltonian for the Linear Chain of Spins
The Hamiltonian that describes the ideal insulated system of a linear chain of N paramagnetic atoms with nuclear spin one half inside the magnetic field
 (1)
(1)
where  and
and  are the amplitude, the angular frequency and the phase of the RF-field, and
are the amplitude, the angular frequency and the phase of the RF-field, and  represents the amplitude of the z-component of the magnetic field, is given by [19]
represents the amplitude of the z-component of the magnetic field, is given by [19]
 (2)
(2)
where  represent the magnetic moment of the kthnucleus, which it is given in terms of the nuclear spin as
represent the magnetic moment of the kthnucleus, which it is given in terms of the nuclear spin as , with
, with  being the proton gyromagnetic ratio and
being the proton gyromagnetic ratio and  being the jth-component of the spin operator,
being the jth-component of the spin operator,  represents the magnetic field, Equation (1) valuated at the location of the kth-nuclear spin
represents the magnetic field, Equation (1) valuated at the location of the kth-nuclear spin . The parameters
. The parameters  and
and  represent the coupling constant at first and second neighbor interaction. The angle between the linear chain and the z-component of the magnetic field is chosen as
represent the coupling constant at first and second neighbor interaction. The angle between the linear chain and the z-component of the magnetic field is chosen as  to eliminate the dipole-dipole interaction between the spins.
to eliminate the dipole-dipole interaction between the spins.
This Hamiltonian can be written as
 (3)
(3)
where  and
and  are defined as
are defined as
 (4)
(4)
and
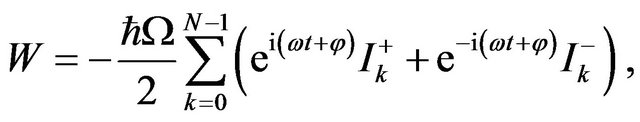 (5)
(5)
where we have used the relation , with the operator
, with the operator  written in terms of Pauli matrixes as
written in terms of Pauli matrixes as . Here we have that:
. Here we have that:  is the Larmor frequency of the kth-spin,
is the Larmor frequency of the kth-spin,  is the Rabi frequency, and
is the Rabi frequency, and  represents the ascend operator
represents the ascend operator  or the descend operator
or the descend operator . The Hamiltonian
. The Hamiltonian  is diagonal in the basis
is diagonal in the basis  with
with  (zero for the exited state and zero for the exited state ). In this work, we consider that the action of the spin operators on its respective qubit is given by
(zero for the exited state and zero for the exited state ). In this work, we consider that the action of the spin operators on its respective qubit is given by
 ,
,  and
and . The eigenvalues of
. The eigenvalues of 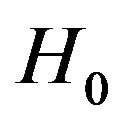 in this basis are given by
in this basis are given by
 (6)
(6)
The elements of this basis forms a register of  - qubits with a total number of
- qubits with a total number of  registers which is the dimensionality of our Hilbert space. The allowed transition of one state to another one is gotten by choosing the angular frequency of the RF-field,
registers which is the dimensionality of our Hilbert space. The allowed transition of one state to another one is gotten by choosing the angular frequency of the RF-field,  , as the associated angular frequency due to the energy difference of these two levels, and by choosing the normalized evolution time
, as the associated angular frequency due to the energy difference of these two levels, and by choosing the normalized evolution time  with the proper time duration (so called RFfield pulse). The set of selected pulses defines the quantum gates and quantum algorithm. The energy difference between two eigenstates of
with the proper time duration (so called RFfield pulse). The set of selected pulses defines the quantum gates and quantum algorithm. The energy difference between two eigenstates of  is
is
 (7)
(7)
with  depending on the state of the first and second neighbor of the kth-quit. Any gate is realized applying RF-pulses of rectangular shape and choosing the radio frequency
depending on the state of the first and second neighbor of the kth-quit. Any gate is realized applying RF-pulses of rectangular shape and choosing the radio frequency  in resonance with the desired transition,
in resonance with the desired transition, . The unitary evolution of the system is denoted by
. The unitary evolution of the system is denoted by , where
, where 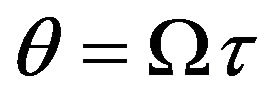 denotes the type of pulse of duration
denotes the type of pulse of duration  [21]. We shall make our study of the teleportation algorithm with this quantum computer with
[21]. We shall make our study of the teleportation algorithm with this quantum computer with .
.
3. Teleportation Algorithm
Denoting by  our three-qubit register, where
our three-qubit register, where
 represents the state to be teleported by Alice,
represents the state to be teleported by Alice, 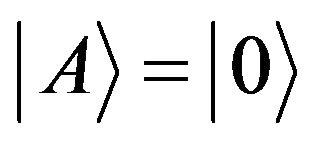 , to Bob,
, to Bob,  , the initial state of our system is given by
, the initial state of our system is given by
 (8)
(8)
where one has used also the decimal notation,
 , meaning that the initial reduced density matrix has the following expression
, meaning that the initial reduced density matrix has the following expression
 (9)
(9)
Then, a resonant  -pulse between the states
-pulse between the states  and
and ,
,  , with frequency
, with frequency , and a resonant
, and a resonant  -pulse between the states
-pulse between the states  and
and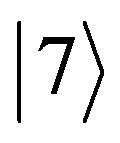 ,
,  , with frequency
, with frequency , are applied to get the state
, are applied to get the state
 (10)
(10)
To put Alice and Bob in an entangled state, a CNOT gate between these elements is done, that is, it is applied a resonant π-pulse between the states  and
and  with frequency
with frequency ,
,  , and a resonant π- pulse between the states
, and a resonant π- pulse between the states  and
and  with frequency
with frequency ,
, 
 , getting the state
, getting the state
 (11)
(11)
Now, to get the teleportation of the state  to Bob, we make an Hadamar gate to the state
to Bob, we make an Hadamar gate to the state , that is, we use a resonant
, that is, we use a resonant  -pulse between the states
-pulse between the states  and
and
 with frequency
with frequency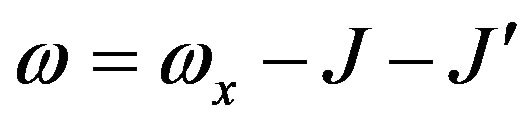 ,
,  , a resonant
, a resonant  -pulse between the states
-pulse between the states  and
and  with frequency
with frequency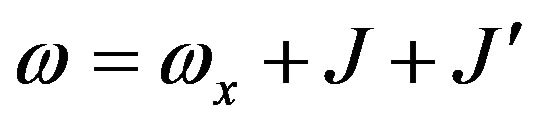 ,
,  , a resonant
, a resonant  -pulse between the states
-pulse between the states  and
and  with frequency
with frequency  and phase
and phase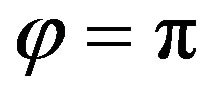 ,
,  , and a resonant
, and a resonant  -pulse between the sates
-pulse between the sates  and
and  with frequency
with frequency  and phase
and phase ,
,  , to get finally the state (binary notation)
, to get finally the state (binary notation)
 (12)
(12)
where  and N represent the identity operator,
and N represent the identity operator,
 , z-Pauli matrix,
, z-Pauli matrix,  , and NOT quantum gate,
, and NOT quantum gate, 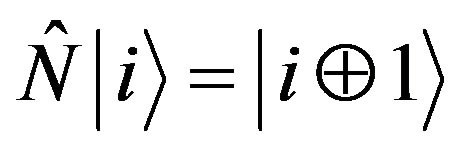 (i = 0,1), acting on the teleported state
(i = 0,1), acting on the teleported state  at Bob location, meaning that all the final density matrix elements would be (without interaction with environment) different from zero. For our numerical studies, we have selected the following coefficients for the state
at Bob location, meaning that all the final density matrix elements would be (without interaction with environment) different from zero. For our numerical studies, we have selected the following coefficients for the state .
.
 (13)
(13)
In summary, one has the following eight pulses to get the teleportation algorithm,


 (14)
(14)
4. System-Environment Interaction Models
Now, to deal with the non ideal situation where the effect of the environment is taken into account, we make use of the Lindblad type master equation for the evolution of the reduced density matrix
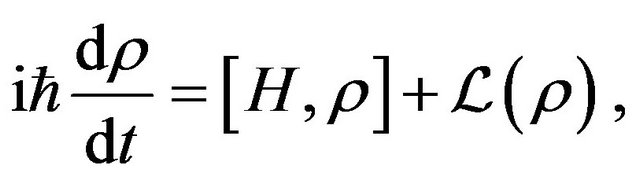 (15)
(15)
where the first part on the right side denotes the usual von Neuman unitary evolution of the reduced density matrix, and the second term represents the Lindblad part (non unitary) evolution. This second term has different expression for different consideration of the system-environment interaction. For the qubits interacting independently with the environment (case (A)), this term has the following form [15]
 (16)
(16)
where  is the dissipative parameter associated to the jth-qubit.
is the dissipative parameter associated to the jth-qubit.
For the pure dephasing interaction case, where the qubits independently dephase to their respective bath with a dephasing rate , the Lindblad term is given by
, the Lindblad term is given by
 (17)
(17)
For the independent-qubit-correlated case (qubits interact with the environment collectively), the Lindblad operator is written as
 (18)
(18)
where one has that  is the decay rate of case (A). In this case, the decay of the state of a qubit has an effect on the other qubits.
is the decay rate of case (A). In this case, the decay of the state of a qubit has an effect on the other qubits.
For the qubit-correlated and dephasing case, with  as the decay rate of the correlated dephasing, the Lindblad operator is given by
as the decay rate of the correlated dephasing, the Lindblad operator is given by
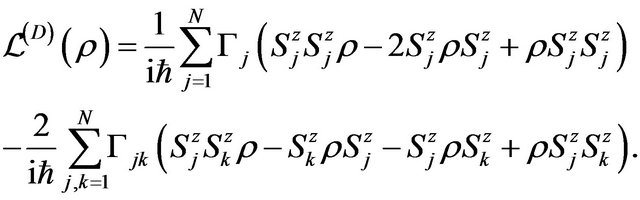 (19)
(19)
In this case, the decay of one qubit affects too the other qubits.
Finally, we define another environmental description for the Lindblad term related to a thermalization process of the system. This system-environment interaction induces an energy absorption process leading the system into a mixed thermalized state. The environment is now at a certain finite temperature, and it can be thought as field radiation modes contained in a cavity where the central system lies. The Lindblad term has the following form [11,24]
 (20)
(20)
where the damping factors are now functions of the temperature and the characteristic frequencies related to the eigenenergies of the closed system. They have the form
 (21)
(21)
and the function
 (22)
(22)
represents the Planck’s distribution function, and  are phenomenological damping factors which depend on the cavity, the eigenfrequencies of the system and the strength of the coupling between the system and the environment. We can manipulate the dissipation parameters by considering a low or high strength of the coupling between the system and the environment, and also some other phenomenological parameters like the volume of the cavity. In this way, we have some freedom to modulate the damping factors. We want to point out that if we go to temperature equals to zero, (the thermal vacuum), the case (A) is recovered since for
are phenomenological damping factors which depend on the cavity, the eigenfrequencies of the system and the strength of the coupling between the system and the environment. We can manipulate the dissipation parameters by considering a low or high strength of the coupling between the system and the environment, and also some other phenomenological parameters like the volume of the cavity. In this way, we have some freedom to modulate the damping factors. We want to point out that if we go to temperature equals to zero, (the thermal vacuum), the case (A) is recovered since for ,
,
 and
and ,
, .
.
The dynamical system for each case for the reduced density matrix elements is deduced from Equation (15) as
 (23)
(23)
where  and
and  represent the elements of the basis of the Hilbert space,
represent the elements of the basis of the Hilbert space,
 and
and .
.
In our case, one has that , the dimensionality of our Hilbert space is eight, and the explicit equations for the dynamical system of each case be see in the appendix of reference [24,25]. We have considered that it is not necessary to repeat those equations in this manuscript.
, the dimensionality of our Hilbert space is eight, and the explicit equations for the dynamical system of each case be see in the appendix of reference [24,25]. We have considered that it is not necessary to repeat those equations in this manuscript.
5. Results of Teleportation Simulation
Our registers are made up of three qubits  with
with , (also denoted as
, (also denoted as , do not confuse with the type of environment) or written them with decimal notation,
, do not confuse with the type of environment) or written them with decimal notation, 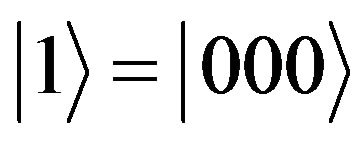 ,
,  and so on. The parameters used for our simulation are taken from [21] and are given (in units of
and so on. The parameters used for our simulation are taken from [21] and are given (in units of ) as
) as
 (24)
(24)
The selected teleported state is defined by the coefficients (13) of the state . Assuming that the environment acts homogeneously on the qubits, the damping parameter can be the same for each qubit, and the damping parameter for correlated cases at second neighbors can be one order of magnitude weaker that at first neighbors. Thus, the dissipative coefficients appearing for the cases (A), (B), (C), and (D) are taken of the following way
. Assuming that the environment acts homogeneously on the qubits, the damping parameter can be the same for each qubit, and the damping parameter for correlated cases at second neighbors can be one order of magnitude weaker that at first neighbors. Thus, the dissipative coefficients appearing for the cases (A), (B), (C), and (D) are taken of the following way

 (25)
(25)
where 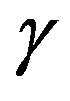 is the free common parameter which takes into account the interaction with the environment. The reduced density matrix is then made up of
is the free common parameter which takes into account the interaction with the environment. The reduced density matrix is then made up of  complex elements, and if the initial reduced density matrix is given by (9).
complex elements, and if the initial reduced density matrix is given by (9).
Figure 1 shows the teleportation algorithm without environment interaction , as seen from the point of view of density matrix elements. The diagonal and real part of non diagonal elements where the coherence of the systems is clearly shown (non diagonal matrix elements have not zero value).
, as seen from the point of view of density matrix elements. The diagonal and real part of non diagonal elements where the coherence of the systems is clearly shown (non diagonal matrix elements have not zero value).
Figure 2 shows the purity behavior at the end of the teleportation algorithm as a function of the dissipative parameter . As we can see, for range of values of gamma in the interval
. As we can see, for range of values of gamma in the interval , this algorithm is well defined except for the thermalization case in which even at that range, the algorithm is totally affected. For higher values the purity decreases and the algorithm is destroyed for all cases. The cases (C) has a similar behavior as (A) case has, and the case (D) has a similar
, this algorithm is well defined except for the thermalization case in which even at that range, the algorithm is totally affected. For higher values the purity decreases and the algorithm is destroyed for all cases. The cases (C) has a similar behavior as (A) case has, and the case (D) has a similar

Figure 1. Matrix elements without environment interaction .
.
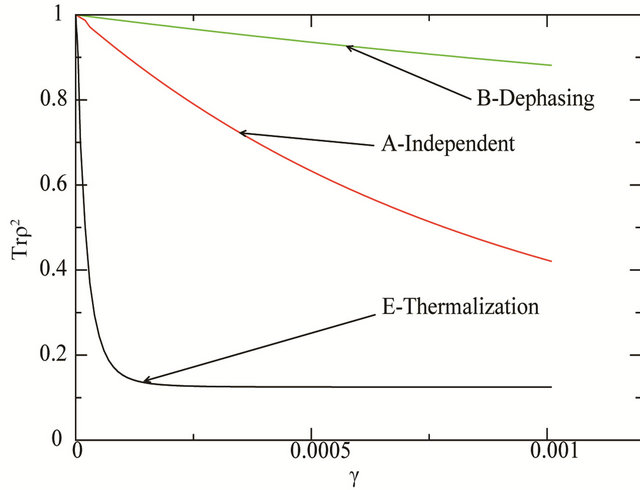
Figure 2. Purity at the end of teleportation algorithm.

Figure 3. Diagonal matrix elements for low (upper) and high (lower) dissipation, and for the cases A (left) and B (right).
behavior as (B) case has. Therefore they are not presented on the figures. The thermalized case is presented for T = 2˚K and the destruction of the algorithm is evident for very low dissipation.
Figure 3 shows the diagonal matrix elements for low  and high
and high  dissipation and for the A and B cases (the results for the C and D cases are similar to these ones). As one could expected, the independent case (A) has much more stronger effect on the algorithm than the dephasing case (B), and for strong dissipation and independent case the system return to a pure system since
dissipation and for the A and B cases (the results for the C and D cases are similar to these ones). As one could expected, the independent case (A) has much more stronger effect on the algorithm than the dephasing case (B), and for strong dissipation and independent case the system return to a pure system since  must be conserved equal to one (the final state is
must be conserved equal to one (the final state is ).
).
Figure 4 shows the behavior of the real part of the matrix elements ,
,  ,
,  , and
, and  for low and high dissipation ranges, and for the case A (independent).
for low and high dissipation ranges, and for the case A (independent).
Figure 5 shows the behavior of the real part of the matrix elements ,
,  ,
, 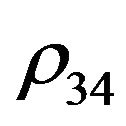 , and
, and  for low and
for low and

Figure 4. Case A, real part of some non diagonal matrix elements for low and high dissipation.

Figure 5. Case B, real part of some non diagonal matrix elements for low and high dissipation.

Figure 6. Purity for the Thermalization process for different values of temperature.
high dissipation ranges, and for the case B (independent).
In Figure 6, we see the transition from the system (Case A) into a thermalized mixed system, when we rise up the temperature for high dissipation range 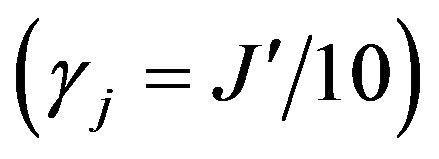 is presented. As we can see, the system goes in to a thermal mixture very rapidly and at relative low temperatures. At zero temperature, there is a different behavior of the purity since the system is recovering purity before the process of the algorithm is ended. So, the resonant pulses used to perform the teleportation gate and the interaction with the environment begin a new dissipation process.
is presented. As we can see, the system goes in to a thermal mixture very rapidly and at relative low temperatures. At zero temperature, there is a different behavior of the purity since the system is recovering purity before the process of the algorithm is ended. So, the resonant pulses used to perform the teleportation gate and the interaction with the environment begin a new dissipation process.
6. Conclusion
We have made a numerical study of decoherence on the teleportation algorithm implemented in a linear chain of three nuclear spins system. We have studied different types of environments, and we have determined the associated decoherence time as a function of the dissipative parameter. We have used the purity value at the end of the algorithm as a quality factor to determine the behavior of the teleportation algorithm. With this parameter and with the selection of the other parameters as (24), we have found that the dissipation parameter to get a well defined quantum gates (without significant decoherence) must be within the range of 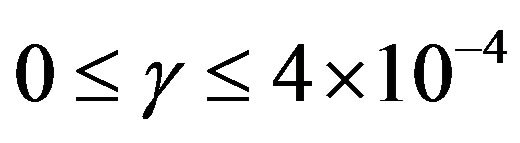 for the non thermalization case. For high dissipation parameter we observed the expected recovery of the purity since
for the non thermalization case. For high dissipation parameter we observed the expected recovery of the purity since  must be conserved. With the selected dissipative coefficients, the cases (C) and (D), corresponding to correlation between spins, have little contribution to the cases (A) and (B) (independent and dephasing cases), and the most danger situation corresponds to the A-independent case when thermalization is not taken into account. However, when thermalization is taken into account, we have shown that even for very low dissipation parameter and very low temperature, the destruction of the algorithm occurs.
must be conserved. With the selected dissipative coefficients, the cases (C) and (D), corresponding to correlation between spins, have little contribution to the cases (A) and (B) (independent and dephasing cases), and the most danger situation corresponds to the A-independent case when thermalization is not taken into account. However, when thermalization is taken into account, we have shown that even for very low dissipation parameter and very low temperature, the destruction of the algorithm occurs.