Path-Integral Derivation of the Transverse Axial Vector and Vector Anomalies in QED ()
1. Introduction
Some time ago Takahashi made the argument for the plausible existence of transverse Ward-Takahashi(WT) relation in canonical field theory, which has the potential to restrict the transverse vertex function from gauge symmetry alone [1]. Subsequently these transverse WT relations for the fermion-boson vertex in coordinate space (or in momentum space) are cast in four-dimensional Abelian gauge theory by computing the curl of the time ordered products of three-point Green functions [2,3]. In addition, the proposed transverse WT relation holds at one-loop order level in four dimensions gauge theory [4]. Up to the effect of quantum anomaly, the possible anomaly for the transverse Ward-Takahashi relations in four dimensional gauge theories is studies by He using the point-splitting method [5]. Recently, the anomaly issue reexamined by means of perturbative method. The conclusion is that there are no transverse anomalies for both the axial vector and vector current [6]. Also the path-integral derivation of the transverse WT relation for the vector vertex and axial vector vertex is presented due to a set of infinitesimal transverse transformation of field variable in QED in Refs. [7,8], wherein Lie group property of the transverse transformation has been illustrated in Abelian gauge theory. Based on the validity of Fujikawa’s analysis, it seemed to us imperative to reevaluate in detail the transverse anomaly of the transverse WT identity for the axial-vector and vector vertex in the QED, which need to be specified. We have done so and find that a careful application of Fujikawa’s approach leads to a transverse quantum anomaly for the axial vector current.
2. Calculation of Anomaly Factor in Ward-Takahashi Identity
From the point of view of path-integral formulation, we proposed a infinitesimal transverse transformation of field variables to derive the WT identities [7,9]. Let us consider a set of infinitesimal local transformation in the QED
 (2.1)
(2.1)
where  stands for the antisymmetry tensor,
stands for the antisymmetry tensor,  and
and  are the fermion and gauge fields, respectively. Here we have suppressed the charge
are the fermion and gauge fields, respectively. Here we have suppressed the charge  prescribed to define the variation of gauge field.
prescribed to define the variation of gauge field.
In principle, the variation of the generating functional itself under the transformation of field variables Equation (2.1) can lead to a Ward-Takahashi type’s identities. The change of the function integral due to the transformation (choosing  for simplicity) gives the relation in momentum space in QED (in the simpler massless fermion) case [3].
for simplicity) gives the relation in momentum space in QED (in the simpler massless fermion) case [3].
 (2.2)
(2.2)
This WT relation for the vector current has been listed in Ref. [9]. The integral term in Equation (2.2) may be called the integral-term involving the vertex function  with the internal momentum $k$ of the gauge boson appearing in the Wilson line [10]. The Fourier transformation for vertex function
with the internal momentum $k$ of the gauge boson appearing in the Wilson line [10]. The Fourier transformation for vertex function  is defined as
is defined as
 (2.3)
(2.3)
where .
.
Obviously, the full vector function and the full axialvector function are coupled with each other. As shown is Ref. [3], the apparent feature of this transverse identity (2.2) is that the vertex function  (fermion’s three point function) has the transverse component of itself.
(fermion’s three point function) has the transverse component of itself.
Completely analogous to the calculations above, let us consider the other transverse transformation
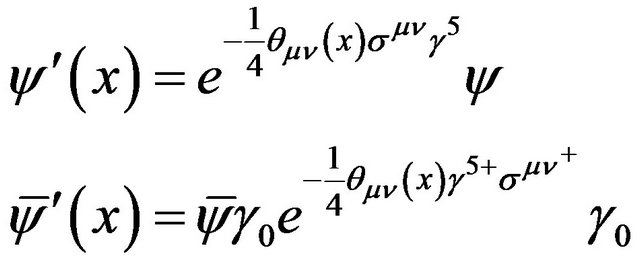 (2.4)
(2.4)
The identity for the axial-vector current is rewritten in momentum space as,
 (2.5)
(2.5)
According to Fujikawa’s interpretation, it is argued that the appearance of the quantum anomaly in WT identity is a symptom of the impossibility of defining a suitably invariant functional integral measure due to the relevant transformations on fermionic field variables. The regularization procedure for the variations of the integral measure can provide access to a wider class of such anomaly objects [11-13]. To see how the change of the measure corresponding to the transverse transformation Equation (2.1) gives rise to a possible anomaly factor, let us consider an Abelian gauge field to show our argument. The Lagrangian density for massive QED, which is of the form
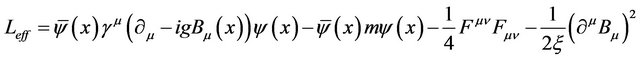 (2.6)
(2.6)
where  and
and  denote, respectively, the charge and mass of the electron. In this case, the gauge field is just the photon field
denote, respectively, the charge and mass of the electron. In this case, the gauge field is just the photon field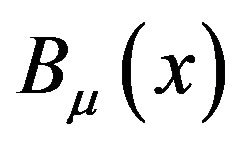 .
.
Thus jacobian  of integral measure due to the transformations Equation (2.1) is evaluated below
of integral measure due to the transformations Equation (2.1) is evaluated below
 (2.7)
(2.7)
This is what we set out to calculate.
Due to the transverse transformation (2.1), the anomaly functions can be written as the limit of a manifestly convergent integral
 (2.8)
(2.8)
where  is the covariant derivative.
is the covariant derivative.
In addition, the transformation of the field  is a translation, so that its Jacobian is trivial.
is a translation, so that its Jacobian is trivial.
The anomaly function  requires regulationwhich is achieved by inserting a regulator
requires regulationwhich is achieved by inserting a regulator
 (2.9)
(2.9)
The expression of the transverse vector anomaly function  can be put in the regulating form
can be put in the regulating form
 (2.10)
(2.10)
In terms of the symmetry of metric and antisymmetry of 4-dimensional field strength tensor, we expand the anomaly function and find that it equals zero. Thus the Jacobian Equation (2.7) becomes
 (2.11)
(2.11)
By the parallel procedure, for the case of the transformation Equation (2.4), the transverse axial vector anomaly function is given by
 (2.12)
(2.12)
The corresponding Jacobian is
 (2.13)
(2.13)
In the above calculation, we have employed the following operator identities
 (2.14)
(2.14)
Obviously the Equations (2.11) is perfectly consistent with result of derivation of transverse vector U(1) anomalies in four-dimensional gauge theory using perturbative methods [5].
3. Concluding Remarks
As already described, Fujikawa’s path-integral method provide a general regularization procedure handling the transverse anomaly factor associated with the WT identity. The calculation shows that there is a quantum anomaly associated with the transverse Ward-Takahashi relation for the axial vector current due to a set of infinitesimal transverse transformation of field variables in QED.
4. Acknowledgements
We would like to thank Professor H. X. He for useful help.