1. Introduction
In [1], the oil-volume marking problem with tilted oil tank is shown and is also a practical one for some oil enterprises.
It is well known that there are several oil tanks and corresponding “oil measuring management system” in gas station, which can measure the input or output oil volumes and the height of the oil in the tank by means of runoff meters and oil height meters. Through a real-time calculation on the relationship between the oil height and the oil volume, we can get the changing conditions of the oil height and the oil volume in the tank. Because of the deformation of the ground work, the oil tanks have been tilted after a period of time of operation, and it needs to remark the oil-volume meter regularly.
The oil volume stored in an inclined cylinder tank is discussed in [2-4] and the oil volume stored in an inclined rectangular parallelepiped tank is studied in [5]. In this paper, the oil tank is more sophisticated geometric shape with a cylinder shape in the middle and two sphere-cal top on both sides. The studying method presented in this paper is: the relationship between the oil volume and the height of the oil is first set up under the situation of no tilting. Secondly, based on the symmetry of the oil tank, the situations of the vertical tilted tank with oil on two sides and on only one side, and the situations of the horizontal tilted tank will be considered by turning into the corresponding oil volume in the situation of no tilting, respectively. Then, the relationship model between the oil volume and 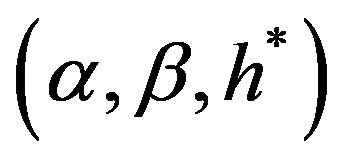 shall be synthesized when the tank tilts not only vertically but also horizontally. Finally, by using non-linear least squares method, parameters
shall be synthesized when the tank tilts not only vertically but also horizontally. Finally, by using non-linear least squares method, parameters 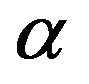 and
and  will be estimated and the marking number of the tank-volume meter will be given.
will be estimated and the marking number of the tank-volume meter will be given.
2. The Oil Volume of the Tank with No Tilting
The tank consists of two differently shaped parts: the main body is a cylinder, the two sides are two spherical top. In order to compute the oil volume, they should be considered respectively (see Figure 1).
From Figure 1, we know that the volume of the shadowed part can be divided into two parts: cylinder part ( ) and spherical body (
) and spherical body (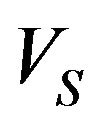 ), and
), and
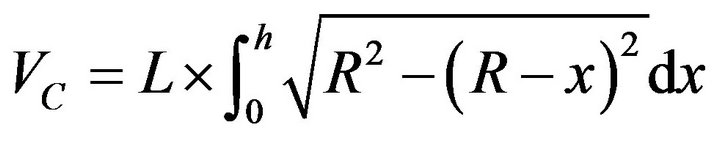 , (2.1)
, (2.1)
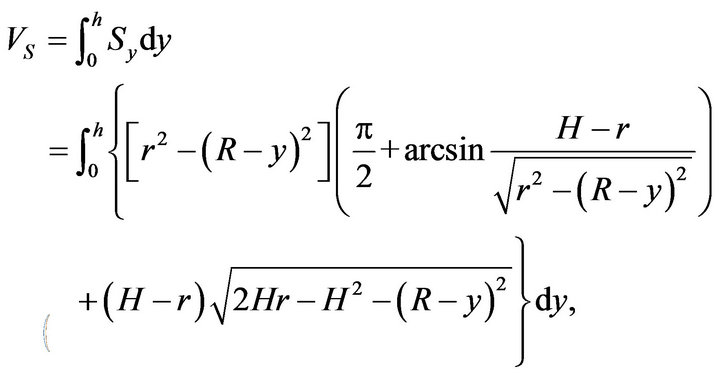 (2.2)
(2.2)
where 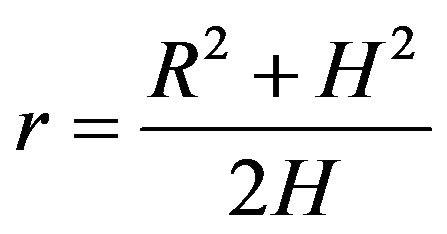
is the radius of the spherical body,  is the radius of the horizontal round section,
is the radius of the horizontal round section,  is the width of the spherical body,
is the width of the spherical body,  is the oil height,
is the oil height,  is the random level section of the spherical body. Let
is the random level section of the spherical body. Let  denote the oil volume of the tank. Then, it follows from (2.1) and (2.2) that
denote the oil volume of the tank. Then, it follows from (2.1) and (2.2) that
 (2.3)
(2.3)
3. The Oil Volume of the Tilted Tank
The tank may tilt vertically or horizontally. Thus, we first consider the influence of vertically tilting angle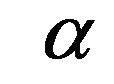 and the horizontally tilting angle
and the horizontally tilting angle  to the oil volume meter, respectively. Then, we shall synthetically study the relationship among the oil volume of the tank, the oil height and the tilted parameter
to the oil volume meter, respectively. Then, we shall synthetically study the relationship among the oil volume of the tank, the oil height and the tilted parameter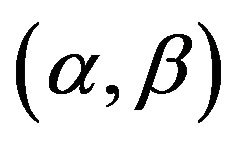 .
.
Based on the known data and the Cartesian coordinate system with taking the center point of the oil tank as origin, it is easy to get the following four equations for boundary contour of the tank:
 (3.1)
(3.1)
Under normal circumstances, when the tank tilts vertically with an angle of 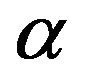 (see Figure 2), the equation of intersection line
(see Figure 2), the equation of intersection line  met by the oil surface and vertical section of the tank can be obtained as follows:
met by the oil surface and vertical section of the tank can be obtained as follows:
 (3.2)
(3.2)
3.1. Situation with Oil on Both Sides
From Figure 3, (3.1) and (3.2), we have
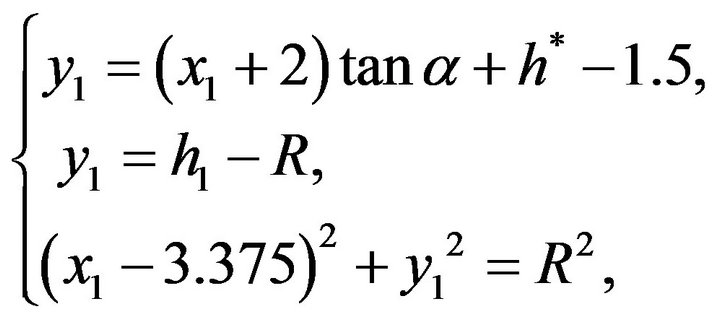 (3.3)
(3.3)
where 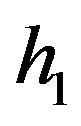 is minimum distance from oil surface to bottom of tank (see Figure 3). Thus, (3.3) implies the following relationship between
is minimum distance from oil surface to bottom of tank (see Figure 3). Thus, (3.3) implies the following relationship between  and
and :
:
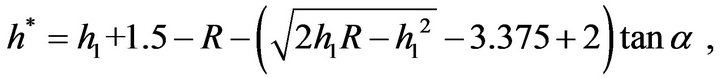
which can be rewritten as
 . (3.4)
. (3.4)
Similarly, let  denote maximum distance from oil surface to bottom of tank (see Figure 3). Then the relationship between
denote maximum distance from oil surface to bottom of tank (see Figure 3). Then the relationship between  and
and  is
is
 i.e.,
i.e.,
 . (3.5)
. (3.5)
By using the method of cutting and filling, the oil volume of the tank can be shown as follows
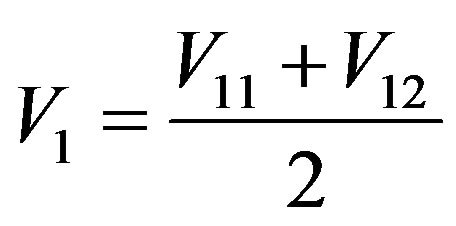 , (3.6)
, (3.6)
where 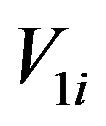 (
(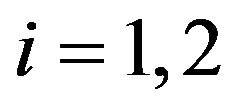 ) can be calculated from (2.3), (3.4) and (3.5) as follows
) can be calculated from (2.3), (3.4) and (3.5) as follows
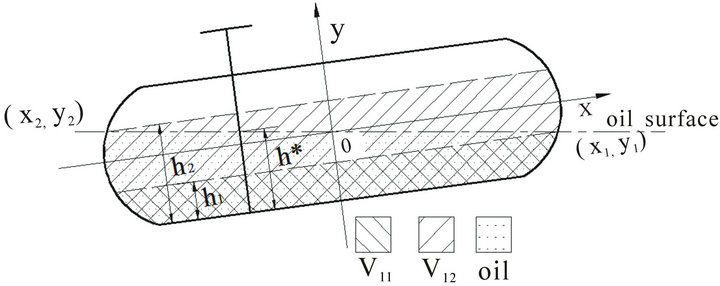
Figure 3. The situation with oil on both sides.
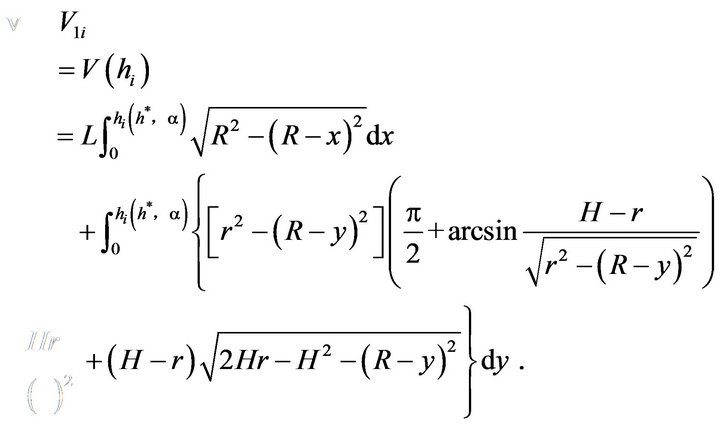
3.2. Situation with Oil on Only One Side
Similarly, let  denote maximum distance from oil surface to bottom of tank (see Figure 4), when the tank in both side has oil on only one side, we have
denote maximum distance from oil surface to bottom of tank (see Figure 4), when the tank in both side has oil on only one side, we have

and the relationship between  and
and  is
is
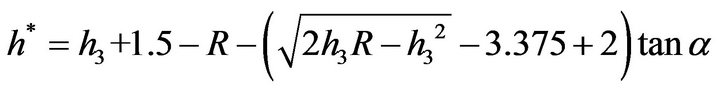 which can be rewritten as
which can be rewritten as
 . (3.7)
. (3.7)
Based on
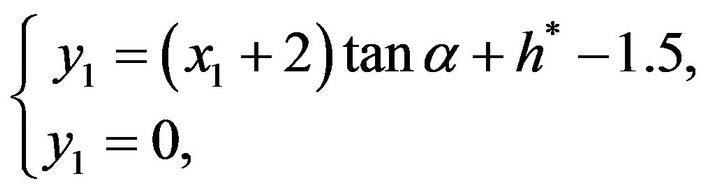
we have
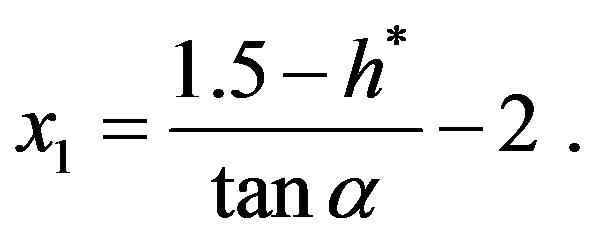
From (2.3) and (3.7), now we know
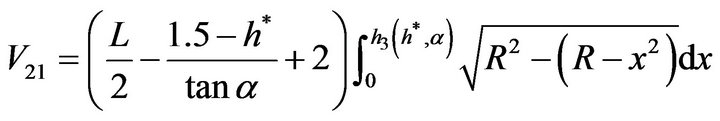 ,
,
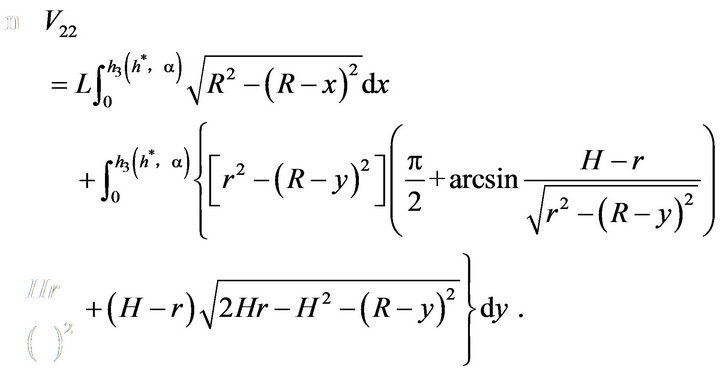
Thus, by using the method of cutting and filling, the oil volume of the tank can be obtained as follows:
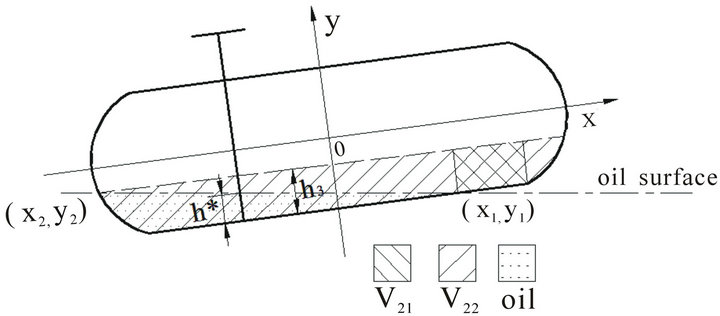
Figure 4. The situation with oil on only one side.
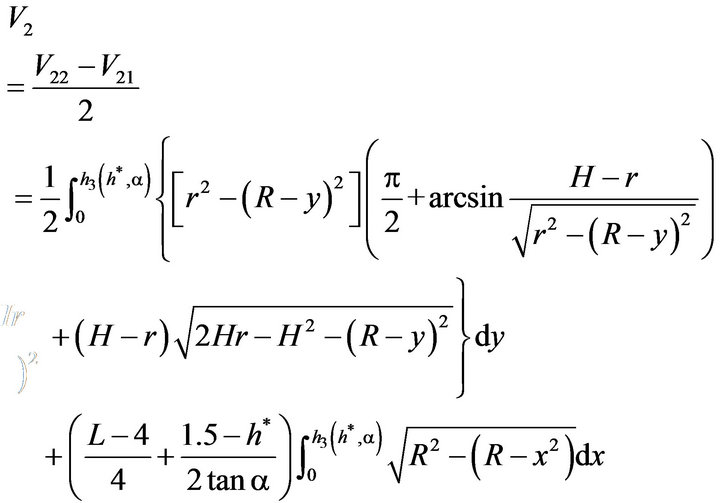 (3.8)
(3.8)
3.3. Horizontally Tilting Model
Because the main body of the tank is a cylinder (center symmetry), both the oil marking stylet and the plumb line pass through the center of its section and the stylet will move with the lean of the tank when the tank tilts horizontally with an angle of . The relation between the oil marking stylet and the plumb line can be shown in Figure 5. Let
. The relation between the oil marking stylet and the plumb line can be shown in Figure 5. Let  denote the real oil height of the tank,
denote the real oil height of the tank,  denote the marking height on the oil meter. Thus, the relationship between
denote the marking height on the oil meter. Thus, the relationship between  and
and  can been shown as follows:
can been shown as follows:
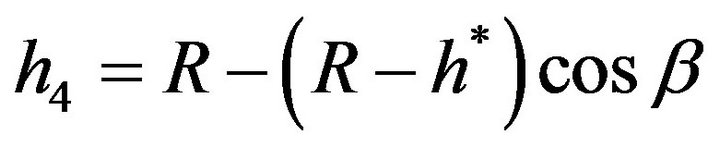 that is
that is
 . (3.9)
. (3.9)
3.4. The Tilted Both Vertically and Horizontally Tank
When the tank is tilted both vertically and horizontally, we replace 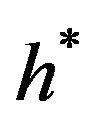 in (3.4), (3.5) and (3.7) by
in (3.4), (3.5) and (3.7) by  in (3.9) and get
in (3.9) and get
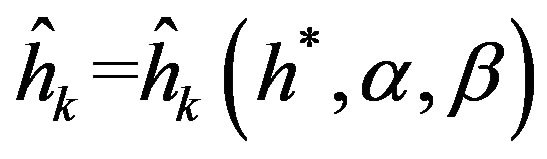 ,
,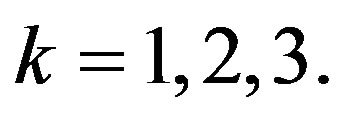 (3.10)
(3.10)
Next, we replace 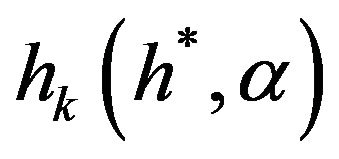 in (3.6) and (3.8) by
in (3.6) and (3.8) by  in (3.10) for
in (3.10) for , and denote the
, and denote the
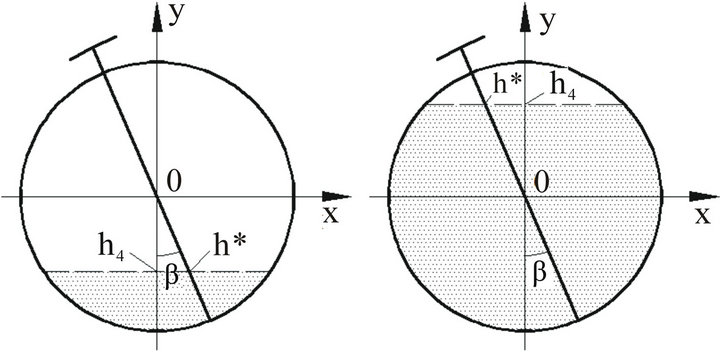
Figure 5. The section sketch map of the horizontally tilted tank.
relationship model between 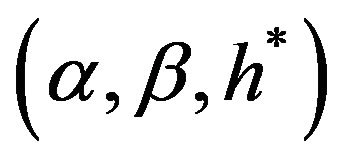 and the oil volume in the situation with oil on both sides and with oil on only one side as follows, respectively:
and the oil volume in the situation with oil on both sides and with oil on only one side as follows, respectively:
 ,
,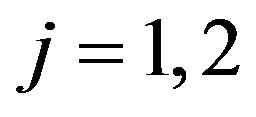 . (3.11)
. (3.11)
• 4. Confirmation of the Parameter and the Marking
• Based on the tested data from 2010 Contemporary Under-gradute Mathmatical Contest in Modeling [1], the oil output 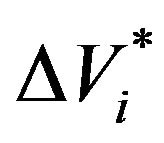 at the different time of day can be obtained. Further, it follows from the relationship model (3.11) that we have
at the different time of day can be obtained. Further, it follows from the relationship model (3.11) that we have
 ,
, .
.
• Thus, we can construct a optimization model for oil-volume marking with tilted oil tank as follows:
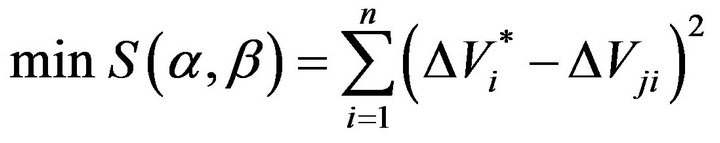 ,
,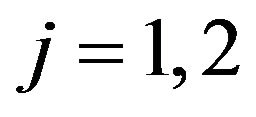 . (4.1)
. (4.1)
• By using nonlinear least squares method, 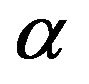 and
and can be estimated.
can be estimated.
• Firstly, thirty groups of data are randomly extracted from the first 302 groups of data. Let the step change of  be 0.05. Then, by (3.1) and (3.2), we can calculate intersecting point of line
be 0.05. Then, by (3.1) and (3.2), we can calculate intersecting point of line  and the edge of the tank and can fix on
and the edge of the tank and can fix on  or
or  in (3.11) based on the intersecting point. Thus, by the model (4.1) and Matlab soft, the minimum relative error between the calculated results and the tested numbers can be confirmed, and the tilting parameters
in (3.11) based on the intersecting point. Thus, by the model (4.1) and Matlab soft, the minimum relative error between the calculated results and the tested numbers can be confirmed, and the tilting parameters  and
and 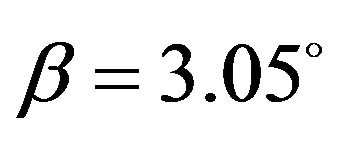 can be computed.
can be computed.
Finally, we have the oil volume of the tilted tank (see Table 1).
5. The Analysis and Test of the Model
In order to test the correctness of the model (3.11), the data after inpouring oil into the tank is used to calculate the oil volumes of the corresponding oil heights, which are analyzed in Excel with the corresponding tested re sults. The maximum of absolute value for the relative error of the corresponding calculated results to the tested number is 2.822%, the minimum of that is 0.001% and the mean of that is 0.577%. By Matlab soft, we compare the tested results with the calculated results after inpouring oil into the tank in Figure 6.
6. Conclusion
Many oil tanks will be tilted after a period of time because of construction, operation or the deformation of ground work, and the oil volume marking of tank will be changed. A number of authors mainly analyzed how to calculate the tank volume, or studied the factors which influence the marking and measuring of oil tanks under the normal situation. In fact, it is very important to study the recognition of the tilted oil tanks and the marking of oil volume.
The purpose of this paper is to construct the optimization model of oil-volume marking with tilted oil tank, to estimate the tilting parameters 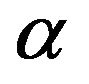 and
and  by using
by using
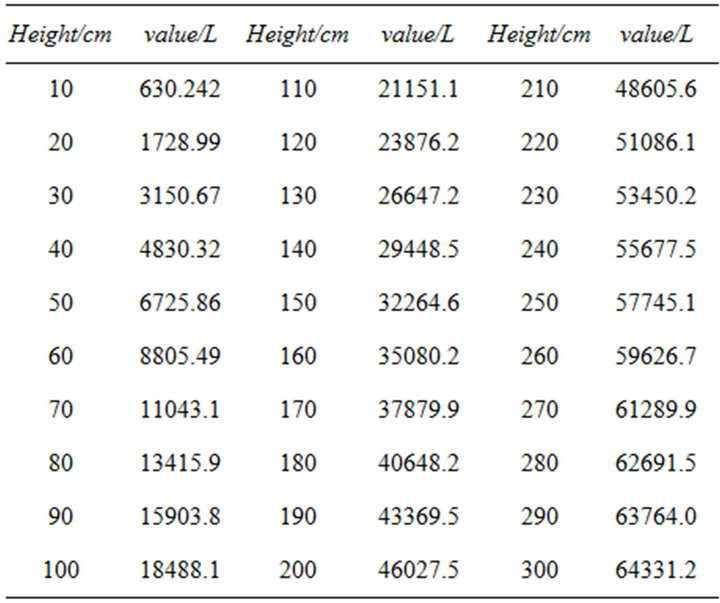
Table 1. The oil volume of the tilted tank.
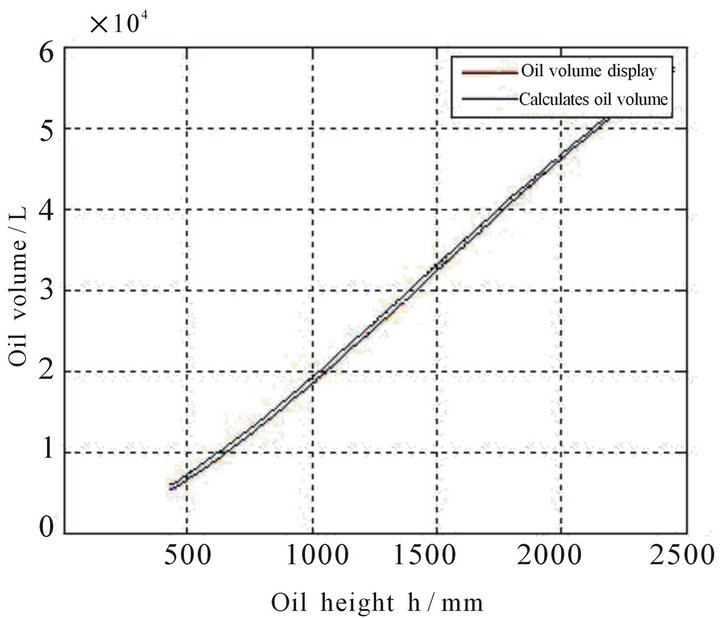
Figure 6. Graph of oil-volume marking and calculated oil volume.
nonlinear least squares method and to give the marking number of the tank-volume meter. Moreover, the optimization model presented in this paper can be used to solve the problem of the oil volume marking when the oil tank is tilted, and can also be applied to solve the volume problems of many containers with various different shapes.
7. Acknowledgements
This work was supported by the Sichuan Youth Science and Technology Foundation (08ZQ026-008), the OpenFoundation of Artificial Intelligence of Key Laboratory of Sichuan Province (2009RZ001) and the Scientific Research Fund of Sichuan Provincial Education Department (10ZA136).