Applications of Mogulskii, and Kurtz-Feng Large Deviation Results to Risk Reserve Processes with Aggregate Claims ()
1. Introduction
There is a wide literature on Large Deviation Techniques and Applications. Relevant to this paper are results by Mogulskii (1993), [1] who proved a Large Deviations result for independent, identically distributed (i.i.d.) random variables with generating functions finite on a neighborhood of the origin. In [2], Lynch and Sethuraman gave large deviations results for stochastic processes with independent and stationary increments. The analysis was done on the space of functions of bounded variation on 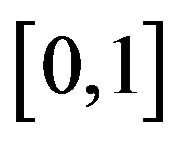 endowed with the weak*-topology. More general results were proved later, as Mogulskii and De Acosta did in [1,3,4] proving large deviations results for Lévy processes in very general settings.
endowed with the weak*-topology. More general results were proved later, as Mogulskii and De Acosta did in [1,3,4] proving large deviations results for Lévy processes in very general settings.
For compound Poisson processes, Li and Pechersky [5], following results by Dobrushin and Pechersky [6], proved the LDP for multi-dimensional compound Poisson processes defined on  with respect to the vague topology, and then strengthened it to the weakuniform topology introduced in [6].
with respect to the vague topology, and then strengthened it to the weakuniform topology introduced in [6].
The LDP for (reserve dependent premium with delayed claims) risk process was studied by Ganesh, Massi and Torrisi (2007) [7,8]. They proved the LDP with respect to the uniform topology in the case of superexponential claims i.e., claims for which the moment generating function is finite for every . Later, in [7], they illustrated the connection between risk processes and queues. They applied their large deviations result (valid only in the case of super-exponential claims) to obtain an approximation for the probability of ruin and to propose an importance sampling parameter for simulation. The super-exponential claims are an interesting but very particular case, since distributions such as gamma (including exponential), Negative Binomial (including geometric) claims, are not of this type.
. Later, in [7], they illustrated the connection between risk processes and queues. They applied their large deviations result (valid only in the case of super-exponential claims) to obtain an approximation for the probability of ruin and to propose an importance sampling parameter for simulation. The super-exponential claims are an interesting but very particular case, since distributions such as gamma (including exponential), Negative Binomial (including geometric) claims, are not of this type.
One way to deal with large deviations for risk processes is by proving the LDP for a sufficiently similar zero-mean Lévy process, and then using the Contraction Principle. That is the general approach we follow for Theorem 1: we examine the LDP for a sequence of risk processes with respect to the Skorohod topology under suitable time and scale modifications. We follow Mogulskii’s approach [1], whose results are based on Lynch and Sethuraman [2] to obtain an LDP for risk processes on  and give quite explicit forms for the rate function.
and give quite explicit forms for the rate function.
Another way to prove Large Deviations results is by first analyzing the compound Poisson component , via working with random walks
, via working with random walks  or their linearized counterpart, proving the LDP, and then dealing with the random time via exponential equivalence of the times. In this direction there is work by Feng and Kurtz, [9] and our Theorem 2 for aggregate claims processes. The difficulty with this approach is that a Poisson process could hardly be exponentially equivalent to a continuous one, and it becomes necessary to use a cumbersome change in time-space scale. We prove Large Deviation results for a wide class of claim distributions including the non-super-exponential case of exponential claims.
or their linearized counterpart, proving the LDP, and then dealing with the random time via exponential equivalence of the times. In this direction there is work by Feng and Kurtz, [9] and our Theorem 2 for aggregate claims processes. The difficulty with this approach is that a Poisson process could hardly be exponentially equivalent to a continuous one, and it becomes necessary to use a cumbersome change in time-space scale. We prove Large Deviation results for a wide class of claim distributions including the non-super-exponential case of exponential claims.
We get the LDP for aggregate claims processes on  with a suitable time-scale modification. Both results are LDP’s with respect to the Skorohod topology induced by the Skorohod distance, but the first one is in
with a suitable time-scale modification. Both results are LDP’s with respect to the Skorohod topology induced by the Skorohod distance, but the first one is in  and the second is in
and the second is in 
Although the vague topology is coarser than Skorohod’s, Li and Pechersky’s large deviations results do not imply ours (Theorem 1 below) because the space  is not reflexive, and non-trivial exponential tightness should be proved first. On the other hand, we do not work with super exponential claims: we only need the moment generating function to exist on an open neighborhood of the origin, and for this reason our result is more general.
is not reflexive, and non-trivial exponential tightness should be proved first. On the other hand, we do not work with super exponential claims: we only need the moment generating function to exist on an open neighborhood of the origin, and for this reason our result is more general.
Large Deviations techniques have been used to study ruin probabilities for risk process. A standard reference here is the book by Asmussen [10], references therein, and subsequent work by the author.
On a generalization of the model, Asmussen, Klüppelberg, and Mikosch, in [11,12], studied asymptotic results for the compound Poisson process when the size of the jumps has a heavy tail (the moment generating function of the claims is  on the positive real numbers). In this case, the large deviations theory does not apply, the results are quite different, and that is not the subject of this paper.
on the positive real numbers). In this case, the large deviations theory does not apply, the results are quite different, and that is not the subject of this paper.
The organization of the paper is as follows: First, we have one Section to state the basic notation, to describe previous results, and at the end we have a small discussion about the precise shape of the rate function: that is Section 2. In Section 3, we state the basic Hypotheses that are needed all along the work.
The main results, LDP Theorems 1 and 2, are stated in Sections 4 and 5, respectively. Both are proved in the same Section they are stated. Section 6 is devoted to the explicit calculations for the case of exponential claims. These calculations are combined in Corollary 1, and later used in Section 7 to estimate the probability of ruin for exponential claims, and also for more general claims.
2. Notation, Previous Results, and the Rate Function
For a random variable  and
and , we denote by
, we denote by  the moment generating function for Y, whenever it exists; its logarithmic generating function is
the moment generating function for Y, whenever it exists; its logarithmic generating function is  and
and
 shall denote the FenchelLegendre transform of
shall denote the FenchelLegendre transform of 
Let 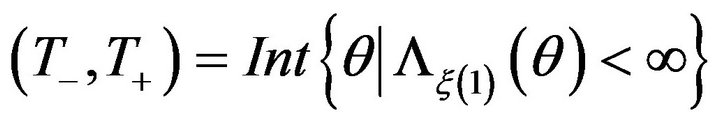 denote the interior of the essential domain for the Laplace transform (and its log-generating function) of
denote the interior of the essential domain for the Laplace transform (and its log-generating function) of 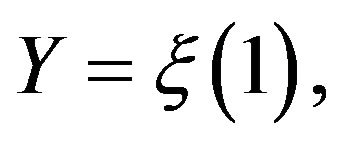 where
where  is a process to be specified.
is a process to be specified.
Clearly, 
The classical risk process is given by
 (1)
(1)
and the following will be our assumptions regarding this process1) 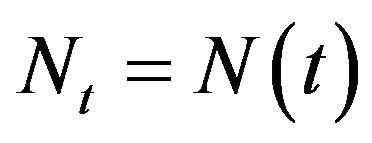 is a Poisson
is a Poisson process,
process,  , that models the number of claims received at time
, that models the number of claims received at time .
.
2)  are non negative i.i.d. random variables with mean
are non negative i.i.d. random variables with mean  independent of the process
independent of the process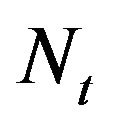 . We shall always assume the moment generating function of
. We shall always assume the moment generating function of ,
, 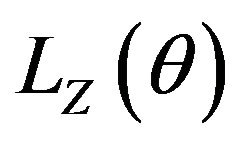 is finite for some
is finite for some  (not necessarily for all
(not necessarily for all ). These variables represent the size of the claims. The compound Poisson term
). These variables represent the size of the claims. The compound Poisson term 
accounts for the aggregate claims.
3)  is the initial capital or reserve.
is the initial capital or reserve.
4)  is positive. The term
is positive. The term  represents the (non random and linear) premiums the company charges.
represents the (non random and linear) premiums the company charges.
It is usually required to have a safety loading condition  to assure ruin does not occur almost surely. We do not need that condition for the moment; however, it shall appear when we give the explicit form of the large deviations rate function.
to assure ruin does not occur almost surely. We do not need that condition for the moment; however, it shall appear when we give the explicit form of the large deviations rate function.
For each bounded variation  with
with  and
and , let
, let  be its standard decomposition such that
be its standard decomposition such that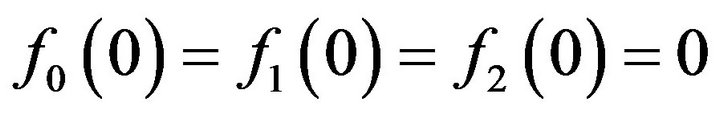 ,
,  is absolutely continuous with respect to the Lebesgue measure (here denoted as
is absolutely continuous with respect to the Lebesgue measure (here denoted as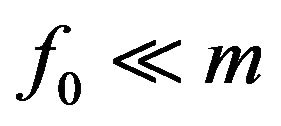 ),
),  is the Hahn-Jordan decomposition for the singular part of f with respect to the Lebesgue measure. Recall that
is the Hahn-Jordan decomposition for the singular part of f with respect to the Lebesgue measure. Recall that  and
and 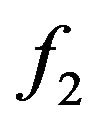 are hence non-decreasing, and each one is singular with respect to
are hence non-decreasing, and each one is singular with respect to  (which shall be denoted
(which shall be denoted ).
).
A standard representation for the characteristic function of a stationary process with independent increments  is
is

with

A regularity condition on the measure  defined by the expression above, which will be needed in the main result (Theorem 1), is:
defined by the expression above, which will be needed in the main result (Theorem 1), is:
 (2)
(2)
and

We shall apply Theorems 2.5 and 2.7 by Mogulskii [1] (see also [2]). We shall write here together all the results we apply, specialized to our settings, and use the notation defined above:
Proposition 1. (Mogulskii) Let  be a stochastic process defined on
be a stochastic process defined on  with values in
with values in  Assume it has stationary independent increments, and also suppose
Assume it has stationary independent increments, and also suppose

If  then ULDP:
then ULDP:  satisfies the upper large deviations principle with respect to the completed Skorohod topology, with good rate function
satisfies the upper large deviations principle with respect to the completed Skorohod topology, with good rate function . LLDP: If, additionally, the regularity condition
. LLDP: If, additionally, the regularity condition
(2) is satisfied, then the same sequence  satisfies the lower large deviations principle with respect to the completed Skorohod topology, with the same rate function
satisfies the lower large deviations principle with respect to the completed Skorohod topology, with the same rate function . The rate function
. The rate function  is
is
 (3)
(3)
where
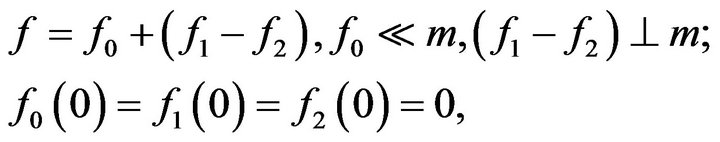
 are non-decreasing, and with the understanding that
are non-decreasing, and with the understanding that  If
If  then the ULDP holds also with the uniform topology.
then the ULDP holds also with the uniform topology.
A Remark on the Rate Function
Remark 1. The rate function I that appears in Mogulskii [1] has two misprints. This can be verified in [2]. It says

whereas it should say

Indeed, for this rate function, Mogulskii refers to the paper by Lynch and Sethuraman ([2]), and according to the latter, the value for  is
is

where  and
and  Without loss of generality, suppose that
Without loss of generality, suppose that  Note that for
Note that for
 hence
hence

If  then
then  and since
and since
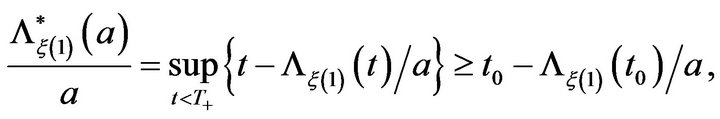
making 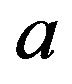 tend to
tend to  we obtain
we obtain

Now, if we let  we conclude
we conclude
 (4)
(4)
On the other hand, for every 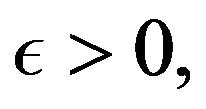 and
and  there is
there is  such that
such that

taking limits as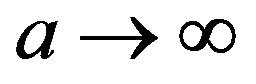 , we conclude
, we conclude
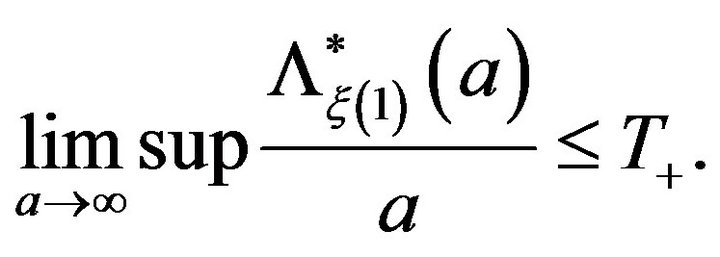 (5)
(5)
In view of formulas (4) and (5) we conclude

With a similar argument we obtain

Finally, since  is non-decreasing and
is non-decreasing and 
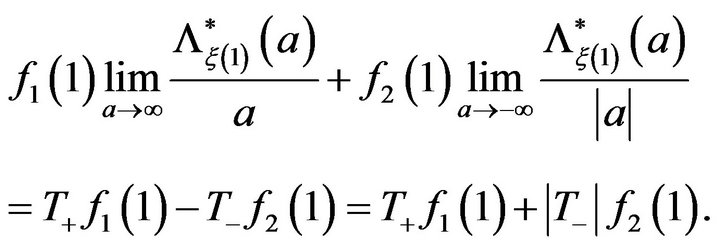
In the next Section we shall state the hypotheses we need.
3. Statement of Hypotheses
Let  be nonnegative independent and identically distributed random variables with mean
be nonnegative independent and identically distributed random variables with mean  and second moment
and second moment  (i.e. Z is non-degenerated).
(i.e. Z is non-degenerated).
Let  be a Poisson process with parameter
be a Poisson process with parameter  defined on the same probability space and independent of the
defined on the same probability space and independent of the  All our random variables Z, and Poisson processes
All our random variables Z, and Poisson processes 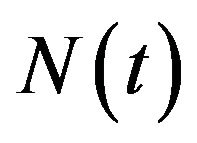 will be as just stated, unless otherwise noted.
will be as just stated, unless otherwise noted.
If  is finite in a neighborhood of the origin, we say Condition 1 is satisfied:
is finite in a neighborhood of the origin, we say Condition 1 is satisfied:
Condition 1. There is  such that
such that
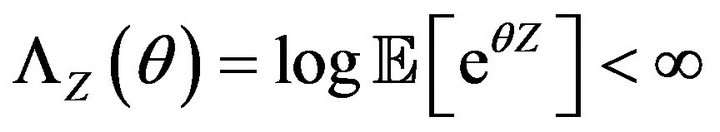 for
for 
Remark 2. Finiteness of the function  is equivalent to that of the moment generating function
is equivalent to that of the moment generating function  Condition 1 is satisfied if
Condition 1 is satisfied if  is finite for some
is finite for some  (the negative part works due to Z being nonnegative).
(the negative part works due to Z being nonnegative).
Notice also that this condition implies , and every moment of the variables
, and every moment of the variables 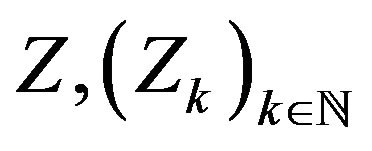 are finite.
are finite.
We shall fix  to be the maximum possible by letting
to be the maximum possible by letting 
To have the LLDP in the topology we want, we require to ask an additional regularity condition:
Condition 2.

Remark 3. All the conditions on Z are satisfied if Z is, for example, exponentially distributed. This important case, for which many calculations can be made explicit, is discussed in Sections 6 and 7.
4. Large Deviations for the Risk Process on

Now we are ready to state the LDP in the space 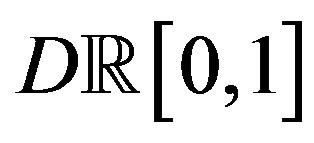 with the Skorohod topology:
with the Skorohod topology:
Theorem 1. Let 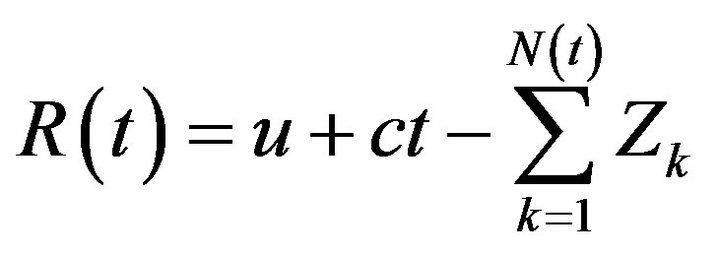 be a risk process as defined in (1). Under conditions 1 and 2, the sequence of processes
be a risk process as defined in (1). Under conditions 1 and 2, the sequence of processes
 (6)
(6)
satisfies the large deviations principle in the space  with the completed topology induced by the Skorohod distance, and rate function
with the completed topology induced by the Skorohod distance, and rate function  defined as
defined as
 (7)
(7)
where  is decomposed as
is decomposed as

and  are non-decreasing.
are non-decreasing.
Remark 4. The form of the rate function is given by
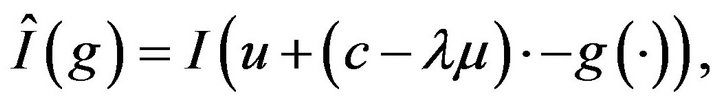 (8)
(8)
with  as in expression (3). We also notice that, in this case,
as in expression (3). We also notice that, in this case, 
Proof of Theorem 1.
Let  be the compound Poisson process. Using the assumptions about
be the compound Poisson process. Using the assumptions about  and N we conclude that
and N we conclude that 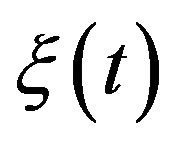 has stationary and independent increments,
has stationary and independent increments,  and that
and that

The Laplace transform  of
of  is
is

We notice that the log-Laplace
 is finite as long as
is finite as long as
 is finite. By Condition 1, we can guarantee that
is finite. By Condition 1, we can guarantee that  is finite for
is finite for  in fact both,
in fact both, 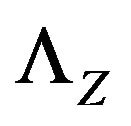 and
and  have the same support. By similar calculations,
have the same support. By similar calculations,

where

which means that the Lévy measure  of this process is
of this process is  times the distribution of the claims
times the distribution of the claims . We notice that if
. We notice that if  is a sequence of sets, then
is a sequence of sets, then
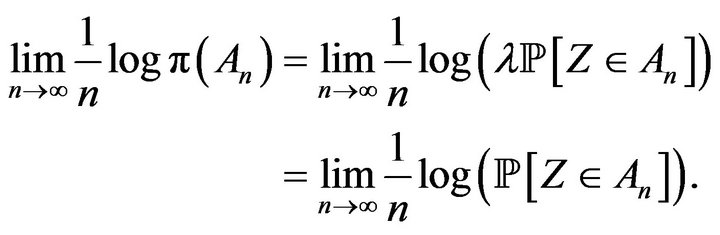
Regarding the Lévy measure  we see that for each
we see that for each  therefore
therefore
 and if
and if , by the Markov inequality,
, by the Markov inequality,

Taking the limit in the previous inequality as n approaches to , and using
, and using  gives us
gives us
 and since this assertion is valid for each
and since this assertion is valid for each  we obtain
we obtain

We observe that by Condition 2,

Since  we conclude that
we conclude that

which is the regularity Condition 2. In summary, the process 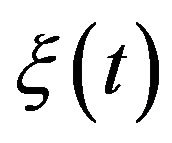 satisfies the hypotheses of Proposition 1, therefore the process
satisfies the hypotheses of Proposition 1, therefore the process

satisfies the LDP with respect to the Skorohod topology with rate function provided by 3.
We now consider  the metric space
the metric space  endowed with the completed topology induced by the Skorohod distance and we also consider the functional
endowed with the completed topology induced by the Skorohod distance and we also consider the functional  defined by
defined by

To verify continuity of F on this specific topology, take  and
and  with
with  in the Skorohod topology. Recall that the Skorohod distance in
in the Skorohod topology. Recall that the Skorohod distance in  is given by
is given by

Then, there is  so that for each
so that for each  we can find
we can find , where
, where 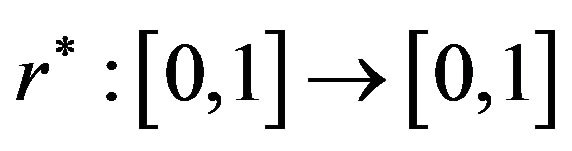 is an non-decreasing continuous function for which
is an non-decreasing continuous function for which
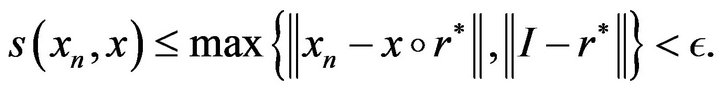
Now,
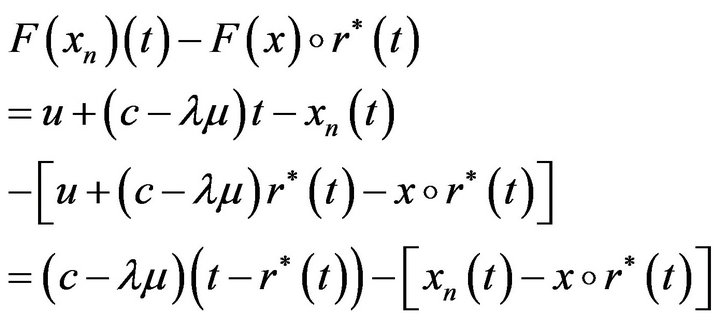
therefore

hence  tends to
tends to  Therefore F is continuous with respect to the Skorohod topology. By the Contraction Principle,
Therefore F is continuous with respect to the Skorohod topology. By the Contraction Principle,

satisfies the LDP with rate function given by

If we consider the Hahn-Jordan decomposition for 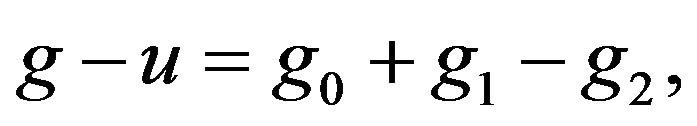 and we observe that
and we observe that 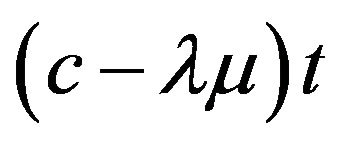 is absolutely continuous with respect to the Lebesgue measure m, we conclude that the Hahn-Jordan decomposition
is absolutely continuous with respect to the Lebesgue measure m, we conclude that the Hahn-Jordan decomposition  for the function
for the function  is
is
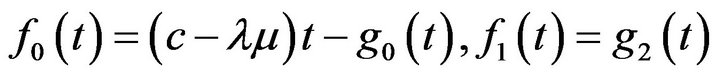 , and
, and
 Evaluating
Evaluating  and using (3), we obtain formula (7), this concludes the proof of Theorem 1. □
and using (3), we obtain formula (7), this concludes the proof of Theorem 1. □
5. Large Deviations for the Aggregate
Claims Process on 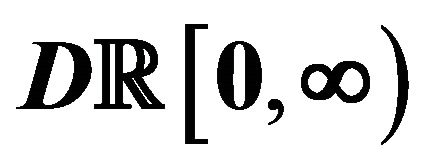
In this Section we prove the LDP for the process of aggregate claims, on a different space, with another time-scale parametrization, and using very different results.
Theorem 2. Assume Condition 1, but now let us denote the Poisson process as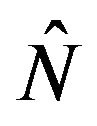 , with parameter
, with parameter  defined on the same probability space and independent of the
defined on the same probability space and independent of the 
Let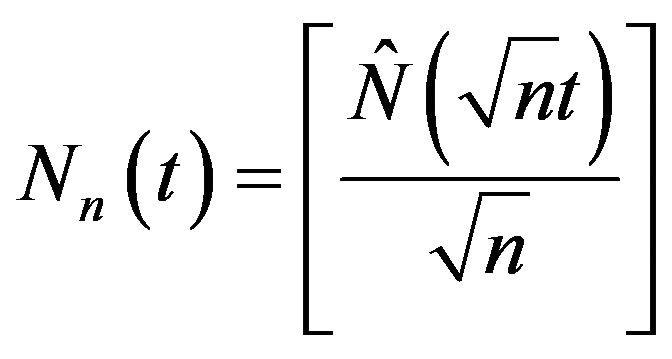 . Then, the sequence of processes
. Then, the sequence of processes

satisfies the large deviations principle in the space 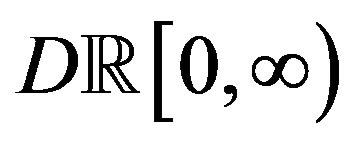 with the topology induced by the Skorohod distance.
with the topology induced by the Skorohod distance.
We will use results from Feng and Kurtz [9], Lemma 4.9 and Theorem 10.1, that we compile in next two Propositions:
Proposition 2. For each  let
let  be a process in
be a process in . Let
. Let  be a nonnegative, nondecreasing process
be a nonnegative, nondecreasing process  valued, independent of
valued, independent of . Define
. Define

Suppose that for each  and
and 
 (9)
(9)
If  is exponentially tight, then the LDP holds for
is exponentially tight, then the LDP holds for 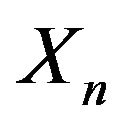 if and only if it holds for
if and only if it holds for .
.
Proposition 3. Let  be given by
be given by

for . Suppose that
. Suppose that  is a solution of the martingale problem for
is a solution of the martingale problem for  and that the LDP holds for
and that the LDP holds for  in
in  with a good rate function
with a good rate function  and rate transform
and rate transform . Then the LDP holds for
. Then the LDP holds for  in
in  with good rate function:
with good rate function:
 (10)
(10)
where
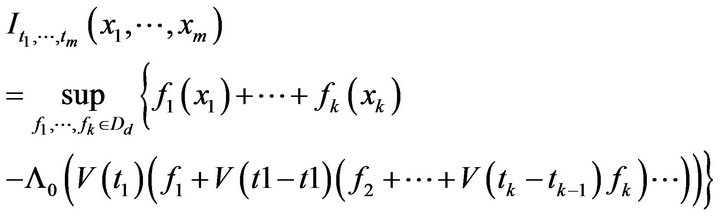
And if  then
then .
.
Proof of Theorem 2.
Let 
Due to the fact that  for some
for some  Proposition 3 can be applied to sequences of processes with independent increments such as
Proposition 3 can be applied to sequences of processes with independent increments such as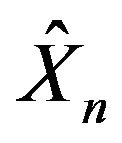 —as discussed in Section 10.2 of Feng and Kurtz [9]. Therefore
—as discussed in Section 10.2 of Feng and Kurtz [9]. Therefore 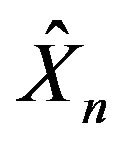 satisfies the LDP with a good rate function defined as in (10). Since this rate function is good, and our space is Polish, then the sequence
satisfies the LDP with a good rate function defined as in (10). Since this rate function is good, and our space is Polish, then the sequence  is exponentially tight in
is exponentially tight in 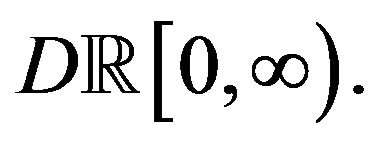
Now, let 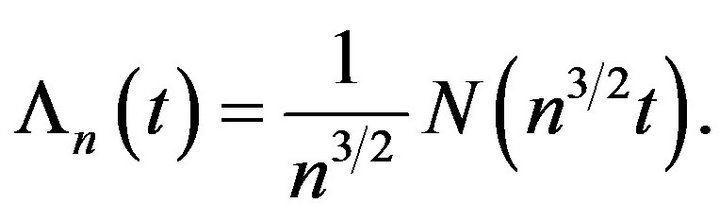 By the MasonShorack, Wellner inequality [13] (p. 545) we have,
By the MasonShorack, Wellner inequality [13] (p. 545) we have,

where  hence
hence

which is (9). Applying Proposition 2 we conclude that
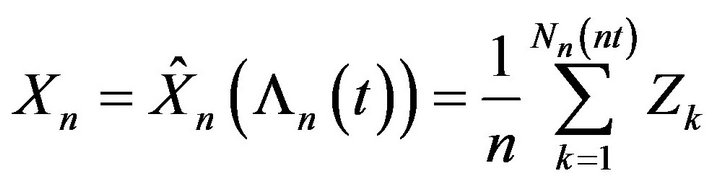
satisfies the LDP with a good rate function. □
6. Exponential Claims
In this Section we give the explicit calculations when the law of the claims is exponential, and we also find the particular shape for the rate function. We have the following Corollary to Theorem 1:
Corollary 1. Consider a classical risk process as defined in (1) with exponentially distributed claims:
 with
with  and
and 
The sequence of processes
 (11)
(11)
satisfies the LDP in the space  with the completed topology induced by the Skorohod distance, and rate function given by
with the completed topology induced by the Skorohod distance, and rate function given by
 (12)
(12)
with

non-decreasing, and .
.
Proof. The Moment Generating function in this case is

hence  if and only if
if and only if  Therefore, Condition 1 holds. In this case
Therefore, Condition 1 holds. In this case
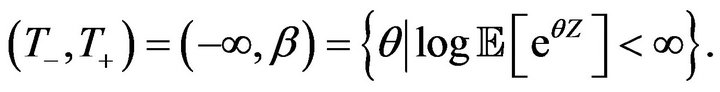
Also,

so Condition 2 also holds.
Applying Theorem 1, we conclude that  satisfies the LDP with rate function given by (7). It remains to show that the rate function has the explicit form (12). Let us calculate, for
satisfies the LDP with rate function given by (7). It remains to show that the rate function has the explicit form (12). Let us calculate, for 

Now
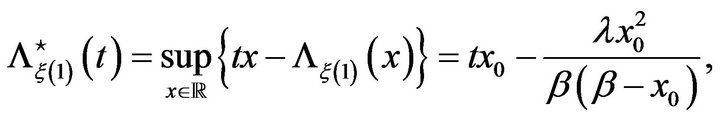
with  if
if  Therefore,
Therefore,
 (13)
(13)
Here, again the Hahn-Jordan decomposition
 for the function
for the function  is
is
 , and
, and
 Therefore,
Therefore,

provided  (otherwise
(otherwise ).
).
Since  the value
the value
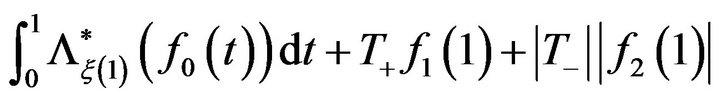 in the rate function (7) provides us information only when
in the rate function (7) provides us information only when  and since
and since  is non-decreasing and
is non-decreasing and  this implies that
this implies that 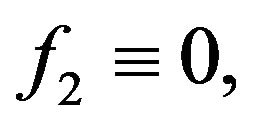 in our case
in our case  Finally,
Finally,  hence the rate function
hence the rate function 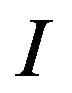 takes the form (12). This proves Corollary 1. □
takes the form (12). This proves Corollary 1. □
7. Estimating the Ruin Probability of the Process Rn
In this section we give an upper bound for the Probability of Ruin for the process  as studied in Section 6 and in Corollary 1; i.e. when the claims are exponentially distributed with parameter
as studied in Section 6 and in Corollary 1; i.e. when the claims are exponentially distributed with parameter 
Theorem 3. For the process  defined in Corollary 1, we have that
defined in Corollary 1, we have that
 (14)
(14)
for sufficiently large n. The estimate is meaningful when
 (15)
(15)
Proof of Theorem 3.
By Corollary 1,  satisfies the LDP with good rate function given by (12), therefore
satisfies the LDP with good rate function given by (12), therefore

for some function  in the essential domain of
in the essential domain of  hence
hence  satisfies:
satisfies:
 where
where 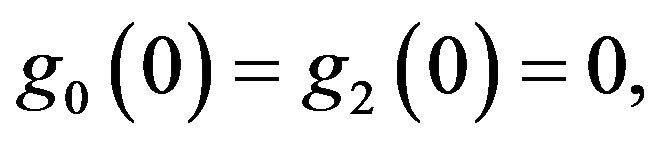
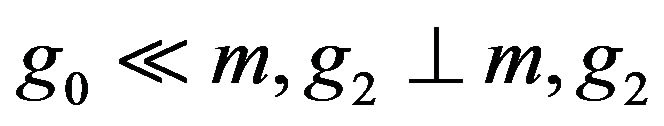 non-decreasing, there is a first time
non-decreasing, there is a first time  when
when 
By definition of  we have
we have
 since
since  is continuous and
is continuous and  is non-decreasing, we conclude that
is non-decreasing, we conclude that

Therefore

the second inequality is due to Jensen’s inequality. Note that  if and only if
if and only if  is above the largest root of the polynomial
is above the largest root of the polynomial  such root is precisely the right hand side of inequality (15). This proves Theorem 3. □
such root is precisely the right hand side of inequality (15). This proves Theorem 3. □
Remark 5. The estimate of the probability ruin provided here for the process  is
is , whereas the exact probability of ruin for the process
, whereas the exact probability of ruin for the process  (seefor instance, Section 1.2 of [14]) is
(seefor instance, Section 1.2 of [14]) is
 Note that the exponent in our estimation also behaves as a polynomial on
Note that the exponent in our estimation also behaves as a polynomial on  of first degree when
of first degree when  is large.
is large.
If the claims are not exponentially distributed, we can still make the following observation regarding the probability of ruin.
Corollary 2. Consider the rate function for the process in Theorem 1, 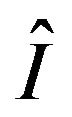 , and let
, and let 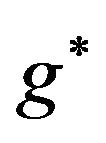 be the dominating point of
be the dominating point of
 with respect to
with respect to . Consider also the decomposition
. Consider also the decomposition
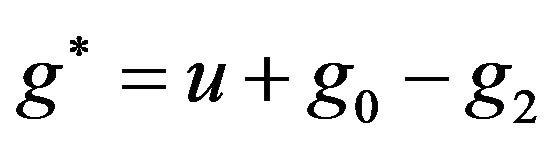 , where
, where
 and with
and with 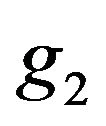 nondecreasing.
nondecreasing.
If  is a solution of
is a solution of
 (16)
(16)
then, for the process  defined in (6), we have
defined in (6), we have
 (17)
(17)
for sufficiently large n.
Recall that the LDP proved in Theorem 1 holds for claims with moment generating functions much less restrictive than the super-exponential case.
Proof of Corollary 2. By Corollary 1,  satisfies the LDP with good rate function
satisfies the LDP with good rate function  given by (7), therefore
given by (7), therefore

where the function  is as in the statement above.
is as in the statement above.
Since
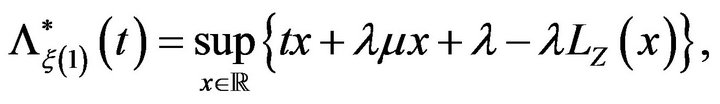
and since  is as in (16), then
is as in (16), then

Finally,

For the second inequality we used the fact that  □
□
8. Acknowledgements
We would like to thank both our universities CSUCI and UNAM, for their hospitality while doing this joint work.
NOTES