Two-Component Substance Basing the Direction Dependence of the Cosmological Deceleration Parameter ()
1. Introduction
The discovering of the accelerating expansion of Universe though observations of distant supernovae [2,3] were stimulated large numbers of articles in which this effect was interprets not only in the framework of general relativity but from other theoretical viewpoints, also. In fact, in [4] it was considered the anisotropic case of the dark energy equation of state; in [5] the anisotropy of cosmic acceleration was searched in the framework of generalized teleparallel gravity; in [6] for the one variant of 5-dimensional inhomogeneous space-time it was found the anisotropic acceleration; in [7] the deceleration anisotropy was considered by usage of baryonic matter Born-Infeld type electrodynamics, and some others attempts [8-11].
Separately to previous variants it’s necessary to mention the fundamental article [12] especially where the asymmetry of Hubble’s diagrams for the North and the South sky hemispheres was searched. (Remind that the Hubble diagram describes in first approximation the linear proportionality between a galaxy’s distance and its redshift. Later on it was found that the velocity at which a distant galaxy is moving from us should be permanently increasing over time, i.e. the cosmic scale factor has a positive second derivative, while deceleration parameter is negative .) This asymmetry, according to authors, cannot be explains by peculiar motion of the observer, but most apparently due to the any bulk flow along the direction ((l, b) = (
.) This asymmetry, according to authors, cannot be explains by peculiar motion of the observer, but most apparently due to the any bulk flow along the direction ((l, b) = ( ,
, )) in the Universe existence that earlier was argued in article [13,14]. Recently R.-G. Cai and Z.-L. Tuo [1] determined more precisely this direction ((l, b) =
)) in the Universe existence that earlier was argued in article [13,14]. Recently R.-G. Cai and Z.-L. Tuo [1] determined more precisely this direction ((l, b) = ,
, )
)
and found the maximum anisotropy of the deceleration parameter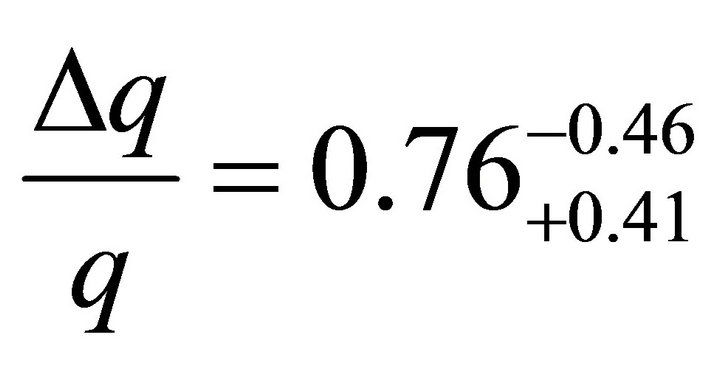 .
.
Evidently, these results are possible to summaries as follows—our Universe is anisotropic in realty and possesses by any principal space axis. That is why the cosmological deceleration parameter will be anisotropic, also and must be depend on the principal space direction in definite way. These statements require theoretical basing the direction dependence of the cosmological deceleration parameter phenomenon.
2. Basic Cosmological Equations
Our searching we start from the well-known results. The uniform isotropic metric of the space-flat Universe ( ) have the standard form
) have the standard form
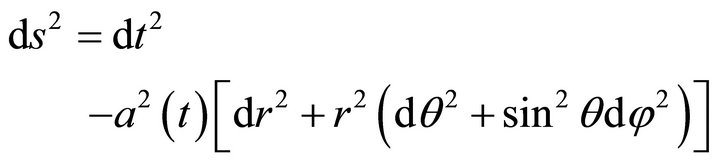 (1)
(1)
Einstein’s equations for the scale factor 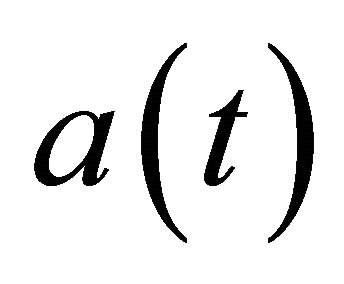 are
are
 (2)
(2)
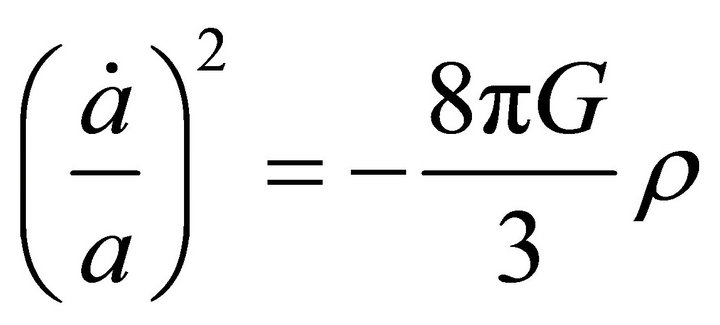 (3)
(3)
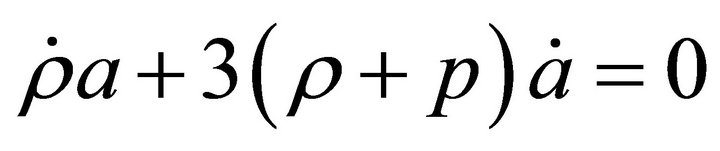 (4)
(4)
These equations is possible to deduce and from the Newtonian mechanics in the following way. Let’s consider the spherical volume of radius  where concentrates any substance with the density
where concentrates any substance with the density 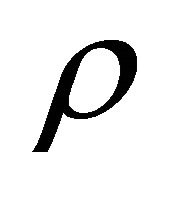 and with the Hubble velocity distribution
and with the Hubble velocity distribution
 (5)
(5)
In the motionless frame of reference the equation of motion of a probe particle that locates on the surface of this sphere, have the usual form
 (6)
(6)
Making the well-known Tolman transformation , that allows taking into account the pressure influence on equation of motion, and putting it into (6) we get Equation (2). Next, multiplying left and right sides of (6) by
, that allows taking into account the pressure influence on equation of motion, and putting it into (6) we get Equation (2). Next, multiplying left and right sides of (6) by  we get Equation (3), that is connected with (6) by the law of energy conservation (4) [15].
we get Equation (3), that is connected with (6) by the law of energy conservation (4) [15].
3. Universe Rotation Axis
In article [16] it was shown that cosmic vacuum produces not only the Universe expansion but its rotation, also. Here the main results of this article are reproducing briefly.
Let’s start from searching the rotational movement of galaxies caused by the antigravitational vacuum force, only. As the model of examining type of galaxy the elliptical galaxy was chosen. For this shape of galaxy its equations of rotational motion are
 (7)
(7)
In (7)  is the first integral of the rotational motion, i.e.
is the first integral of the rotational motion, i.e.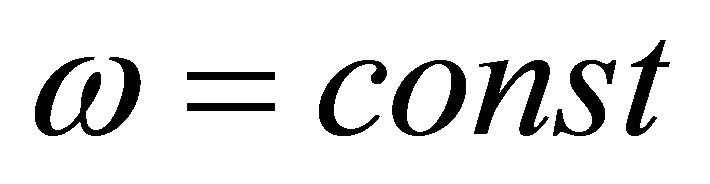 . It describes the component of angular velocity with respect to the specific momentum—C. Next, at deducing (7) it was put forward condition that galaxy angular velocity is very small. This allowed neglect the squared angular velocity components and the corresponding angular accelerations. And at last, it was assumed that arbitrary potential in (7) equals to the vacuum potential
. It describes the component of angular velocity with respect to the specific momentum—C. Next, at deducing (7) it was put forward condition that galaxy angular velocity is very small. This allowed neglect the squared angular velocity components and the corresponding angular accelerations. And at last, it was assumed that arbitrary potential in (7) equals to the vacuum potential , where
, where
 (8)
(8)
Analysis of Equation (7) shown that solution for the precession angle evolving is . Basing on this result it is easy to calculate the angular velocity of the elliptical galaxy around
. Basing on this result it is easy to calculate the angular velocity of the elliptical galaxy around  axis. As for this case the following condition
axis. As for this case the following condition  takes place, than its module equals
takes place, than its module equals
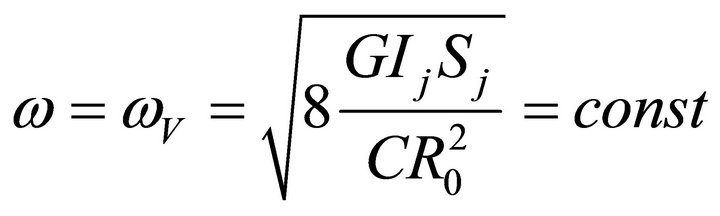 (9)
(9)
This expression describes the angular velocity that galaxy acquires due to the vacuum antigravitational force.
Admitting 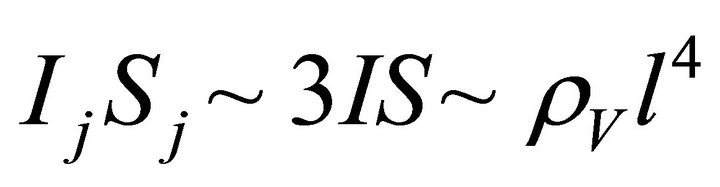 and putting that
and putting that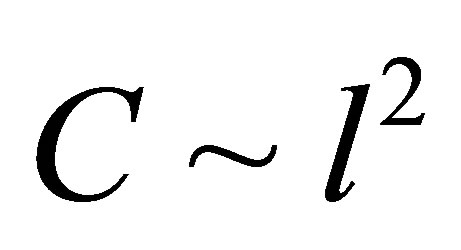 we find
we find . So, its maximal magnitude will be under the condition
. So, its maximal magnitude will be under the condition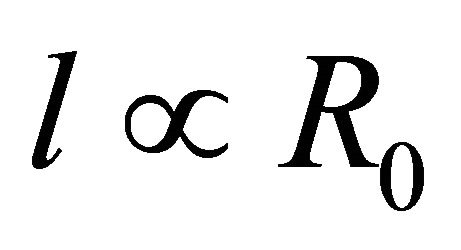 . Then expression for the vacuum angular velocity simplifies and takes on the form
. Then expression for the vacuum angular velocity simplifies and takes on the form
 (10)
(10)
This expression interprets as the minimal angular velocity in the Universe that possesses an arbitrary object due to the vacuum presence. Its present numerical value is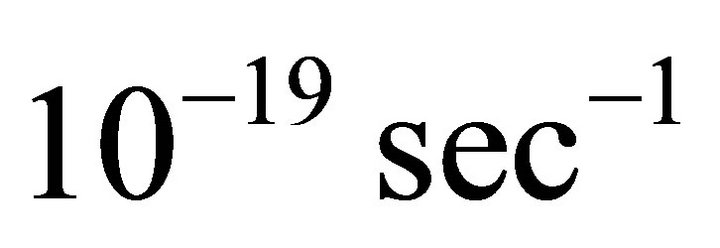 . Hence, the vacuum creates the identical initial angular velocity for all of cosmic objects, includeing the Universe itself.
. Hence, the vacuum creates the identical initial angular velocity for all of cosmic objects, includeing the Universe itself.
At the earliest stages of the Universe evolution, for instance at the baryonic asymmetry epoch when vacuum density was 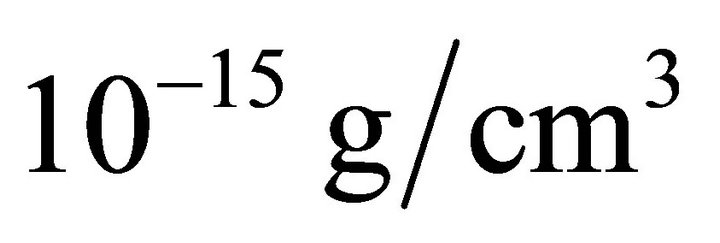 of order, the angular velocity occurs equal
of order, the angular velocity occurs equal . For the very early Universe when vacuum density was—
. For the very early Universe when vacuum density was—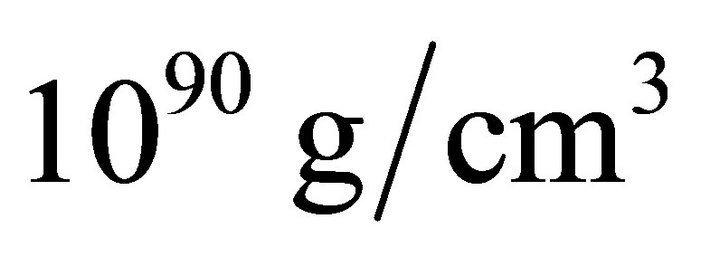 , the Universe angular velocity is
, the Universe angular velocity is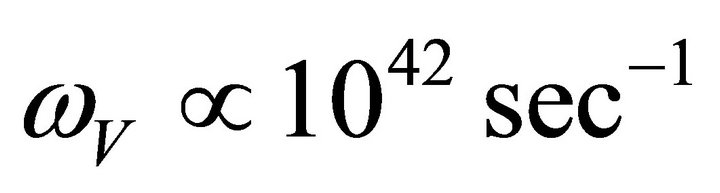 . This magnitude practically equals to the result of article [17], which was done in the framework of general relativity theory (
. This magnitude practically equals to the result of article [17], which was done in the framework of general relativity theory ( ).
).
Henceforth, from these investigations we get the following conclusion—the Universe rotation leads to picking out the principal direction in the space, it may be named as the Universe rotation axis. (Mark, that measurement along this axis only gives the Hubble parameter for the uniform Universe, because in the perpendicular directions the Carioles and centrifugal forces act, also).
4. Basing the Direction Dependence of the Cosmological Deceleration Parameter
For enriching our target, which was formulated in Section 1, put that distance
 (11)
(11)
where  is the distance in uniform space, while
is the distance in uniform space, while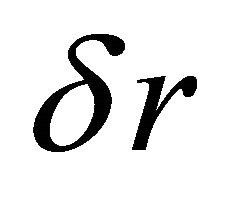 — small addition (perturb term) for describing the possible space anisotropy. Putting (11) into the Newtonian Equation (6) we get the equation
— small addition (perturb term) for describing the possible space anisotropy. Putting (11) into the Newtonian Equation (6) we get the equation
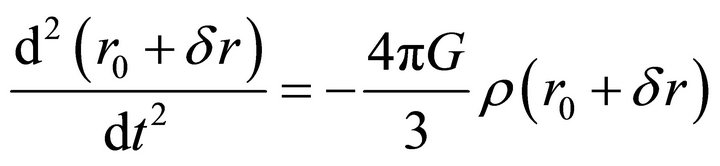 (12)
(12)
that may be decomposed on two parts, easily: main part
 (13)
(13)
and perturb one
 (14)
(14)
Later on these equations will be considered as are independent each other.
Performing the above mentioned Tolman transformation 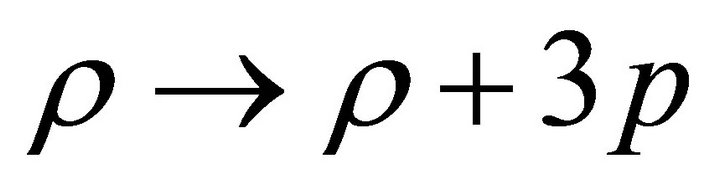 and substituting it into (13) we find equation
and substituting it into (13) we find equation
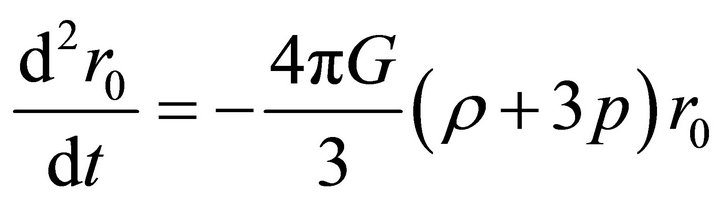 (15)
(15)
For the case of vacuum ( ,
,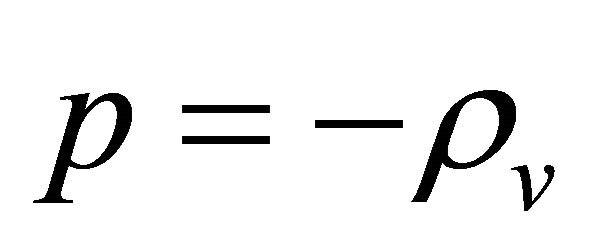 ) the inflationary regime of the Universe expanding follows from (15) immediately—
) the inflationary regime of the Universe expanding follows from (15) immediately—
 (16)
(16)
It leads to the Hubble expansion law
 (17)
(17)
and to the corresponding acceleration
 (18)
(18)
Now consider the Equation (14). Suppose that in this equation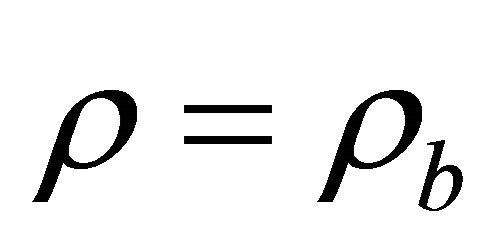 , where
, where 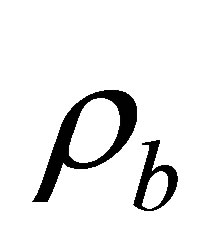 is the baryonic substance density. The baryonic substance pressure
is the baryonic substance density. The baryonic substance pressure 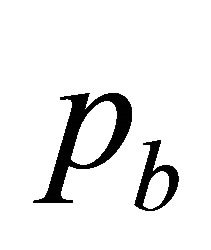 let equals zero, for simplicity. Last requirement means considering the presence of two-component substance—cosmic vacuum and baryonic dust—in the Universe, that are not interact each other in the main approximation.
let equals zero, for simplicity. Last requirement means considering the presence of two-component substance—cosmic vacuum and baryonic dust—in the Universe, that are not interact each other in the main approximation.
By introducing the designation , from (14) it follows
, from (14) it follows
 (19)
(19)
This oscillatory-type equation possesses by two roots
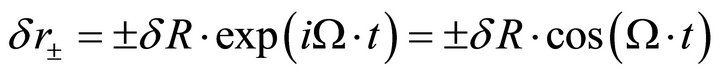 (20)
(20)
They lead to the presence of two perturb (with respect to (17)) velocities
 (21)
(21)
and two corresponding accelerations
 (22)
(22)
From physical viewpoint expressions (20)-(22) mean that presence of baryonic dust matter creates two spaceopposite fluxes that are propagate on the background of expanding and accelerating “Hubble vacuum flux” along the Universe rotation axis (see division 3). That is why it possible writes down the expressions for total distance, velocity and acceleration of any probe particle (galaxy)
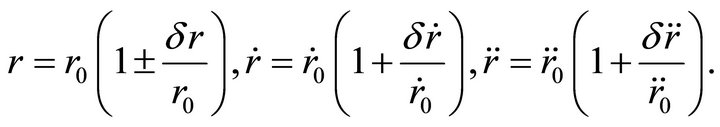 (23)
(23)
Thus the cosmological deceleration parameter q with the accuracy no higher than 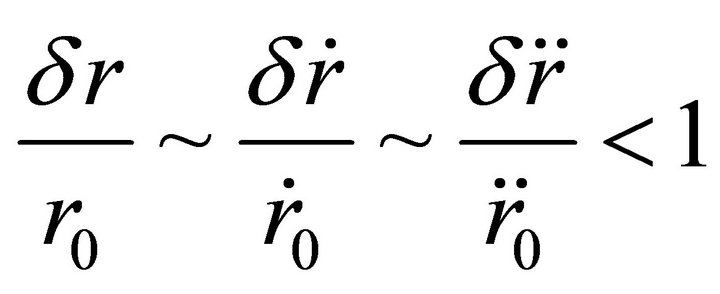 is
is
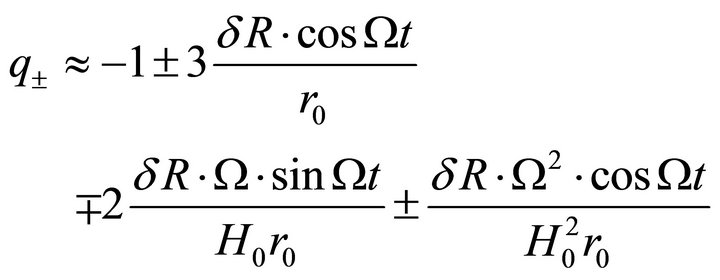 (24)
(24)
Basing on the definitions of  and
and  we introduce the new coefficient
we introduce the new coefficient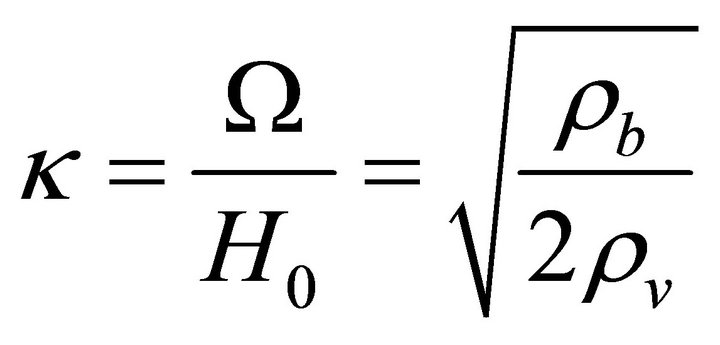 . As in unit of the critical density
. As in unit of the critical density 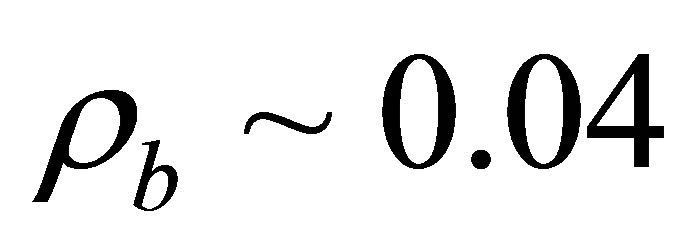 and vacuum density
and vacuum density , coefficient
, coefficient , henceforth.
, henceforth.
From (24) it is possible find the relative acceleration difference between two baryonic fluxes with respect to the “Hubble vacuum flux”—
 (25)
(25)
Assuming that for modern epoch  we approximately get
we approximately get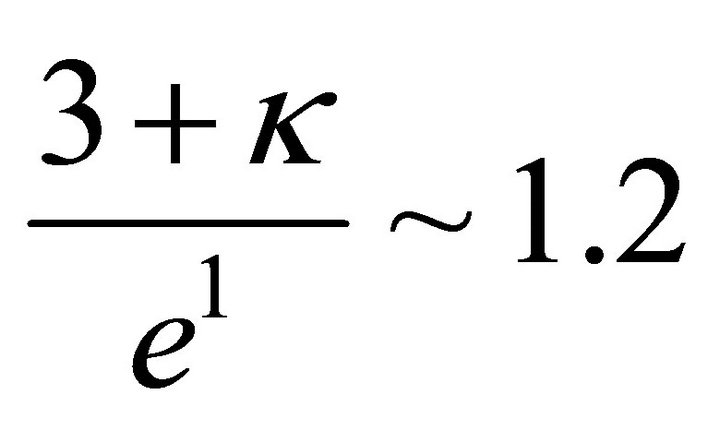 . Hence, the first term in right side of (25) tends to 1.2, while the second term tends to zero. So,
. Hence, the first term in right side of (25) tends to 1.2, while the second term tends to zero. So,
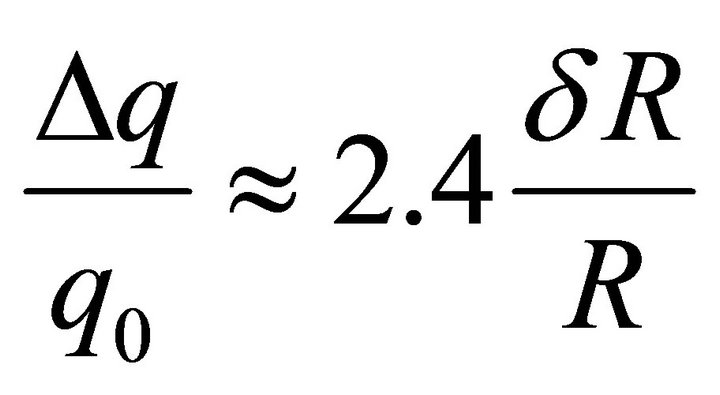 (26)
(26)
Basing on our assumption , that was argued earlier, we may put that it will satisfy if the ratio
, that was argued earlier, we may put that it will satisfy if the ratio 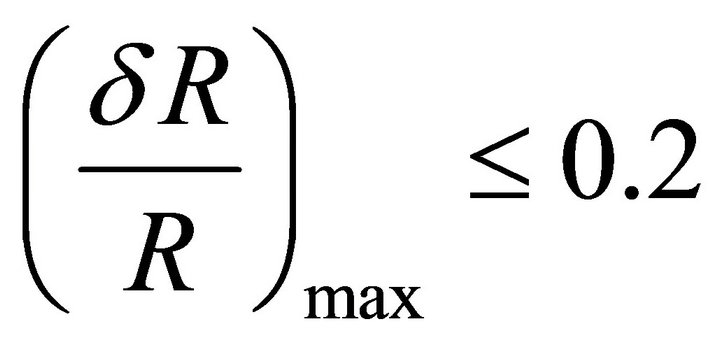 . This leads to the estimation
. This leads to the estimation  that is in good correlation (case of the upper magnitude index) with the value
that is in good correlation (case of the upper magnitude index) with the value  in [1].
in [1].
5. Conclusion
From observational data it was established the asymmetry of Hubble’s diagrams for the North and the South sky hemispheres [13,14]. Moreover it was estimated the space anisotropy of the deceleration parameter phenomenon, that was done by R.-G. Cai and Z.-L. Tuo. These facts require the adequate theoretical basing, hence.
For doing this the concepts of Universe vacuum rotation and its two independent component model (cosmic vacuum and baryonic dust) were attracted. Our result on the phenomenon of anisotropy the deceleration parameter calculation—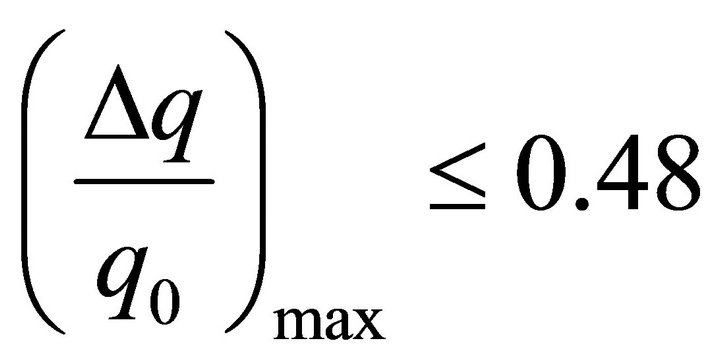 —is in good correlation
—is in good correlation
(case of the upper magnitude index) with the value
 , which was evaluated in [1].
, which was evaluated in [1].
6. Acknowledgements
I would like to express the gratitude to Ministry of Education and Sciences, Republic of Kazakhstan for supports this searching in the framework of budget program 055, subprogram 101 “Grant financing of the scientific researchers”.
Also I thank a reviewer for his thought-out suggestions on the article’s content clarifying.