1. Introduction
With the rapid growth of on-line information, text categorization has become one of the key techniques for handling and organizing data in textual format. Text categorization techniques are an essential part of text mining and are used to classify new documents and to find interesting information contained within several on-line web sites. Since building text classifiers by hand is difficult, time-consuming and often not efficient, it is worthy to learn classifiers from experimental data. In this proposal we employ a generative approach for the analysis of textual data. In the last two decades many interesting and powerful contributions have been proposed. In particular, when coping with the text classification task, a researcher has to face the well-known problem of polysems (multiple senses for a given words) and synonyms (same meaning for different words). One of the first effective model able to solve those issues is represented by Latent semantic analysis (LSA) [1]. The basic idea is to work at a semantical level by reducing the vector space through Singular Value Decomposition (SVD), producing not sparse occurrence tables that help in discovering associations between documents. In order to establish a solid theoretical statistical framework in this context, in [2] a probabilistic version of LSA (pLSA) has been proposed, also known as the aspect model, rooted in the family of latent class models and based on a mixture of conditionally independent multinomial distributions for the couple words-documents. The intention from the introduction of pLSA was to offer a formal statistical framework, helping the parameter interpretation issue as well. By the way the goal was achieved only partially, in fact the multinomial mixtures, which components can be interpreted as topics, offer a probabilistic justification at words but not at documents level. In fact the latter are represented merely as list of mixing proportions derived from mixture components. Moreover, the multinomial distribution presents as many values as there are in the training documents and therefore it learns topic mixture on those trained documents. The extension to previously unseen documents is not appropriate since there can be new topics. In order to overcome the asymmetry between words and documents and to produce a real generative model, [3] proposed the LDA (Latent Dirichlet Allocation). The idea of such new approach emerges from the concept of exchangeability for the words in a document that unfolds in the “bag of words” assumption: the order of words in a text is not important. In fact the LDA model is able to capture either the words or documents exchangeability unlike LSA and pLSA. On the other hand LDA is a generative model in any sense since it posits a Dirichlet distribution over documents in the corpus, while each topic is drawn from a Multinomial distribution over words. However note that [4] in 2003 have shown that LDA and pLSA are equivalent if the latter is under a uniform Dirichlet prior distribution. Obviously LDA does not solve all the issues. The main restriction embedded in LDA approach and due to the Dirichlet distribution, is the assumption of independence among topics. The immediate consequence was to tackle the issue by introducing the Correlated Topic Model (CTM), as proposed in [5]. CTM introduces correlations among topics by replacing the Dirichlet random variable with the logistic normal distribution. Unlike LDA, CTM presents a clear complication in terms of inference and parameter estimation since the logistic normal distribution and the Multinomial are not conjugate. To bypass the problem, the most recent alternative is represented by the Independent Factor Topic Models (IFTM) introduced in [6]. Such proposal makes use of latent variable model approach to detect hidden correlations among topics. The choice to explore the latent model world allows to choose among several alternatives ranging from the type of relation, linear or not linear, to the type of prior to be specified for the latent source. For sake of completeness is important to mention another interesting research path focusing on the burstiness phenomenon, that is the tendency of rare words, mostly, to appear in burst. The above mentioned generative models are not able to capture such peculiarity, that instead is very well modelled by the Dirichlet Compund Multinomial model (DCM). Such distribution was introduced by statisticians [7] and has been widely employed by other sectors like bioinformatics [8] and language engineering [9]. An important contribution in the context of text classification was brought by [10] and [11] that profitably used DCM as a bag-of-bags-of-words generative process. Similarly to LDA, we have a Dirichlet random variable that generates a Multinomial random variable for each document from which words are drawn. By the way, DCM cannot be considered a topic model in a way, since each document derives specifically by one topic. That is the main reason why [12] proposed a natural extension of the classical topic model LDA by plugging into it the DCM distribution and obtaining the so called DCMLDA. Following this line of thinking, we move from DCM approach and we propose an extension of the DCM, called “semanticbased Dirichlet Compound Multinomial” (sbDCM), that permits to take latent topics into account. The paper is organized as follows: in Section 2 we show the Dirichlet Compound Multinomial (DCM) model, in Section we propose an extension of the DCM, called “semanticbased Dirichlet Compound Multinomial” (sbDCM), in Section 4 we show how to estimate the parameters of the different models. Then, in Section 5 we assess the predictive performance of the two distributions by using seven different classifiers. Finally we show the different classification performance according to the knowledge on the topics T (known or unknown).
2. Background: The Dirichlet Compound Multinomial
The DCM distribution is a hierarchical model: on one hand, the Dirichlet random variable is devoted to model the Multinomial word parameters q; on the other hand, the Multinomial variable models the word count vectors 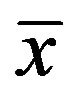 comprising the document. The distribution function of the DCM mixture model is:
comprising the document. The distribution function of the DCM mixture model is:
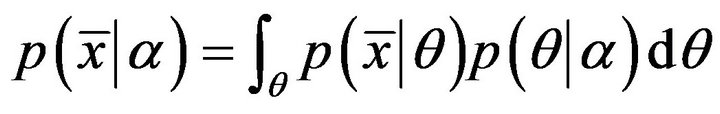 . (1)
. (1)
where  is the Multinomial distribution:
is the Multinomial distribution:
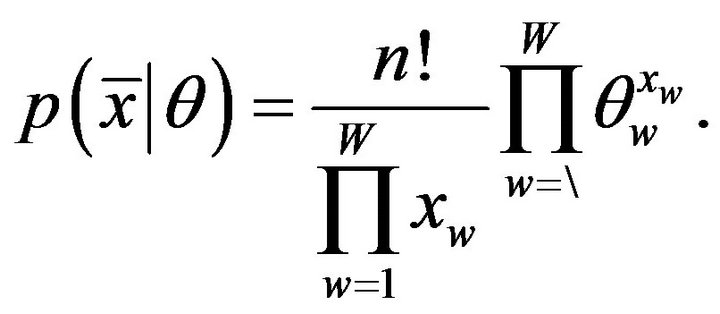 (2)
(2)
in which 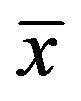 is the words count vector, xw is the count for each word and qw the probability of emitting a word
is the words count vector, xw is the count for each word and qw the probability of emitting a word ; therefore a document is modelled as a single set of words (“bag-of-words”). The Dirichlet distribution
; therefore a document is modelled as a single set of words (“bag-of-words”). The Dirichlet distribution  is instead parameterized as:
is instead parameterized as:
 (3)
(3)
with 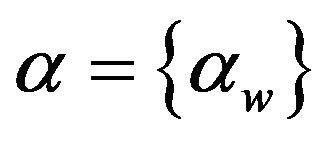 the Dirichlet parameter vector for words, as consequence the whole set of words (“bag-of-bags”) is modelled. Thus a text (a document in a set) is modelled as “bag-of-bags-of-words”. Developing the previous integral we obtain:
the Dirichlet parameter vector for words, as consequence the whole set of words (“bag-of-bags”) is modelled. Thus a text (a document in a set) is modelled as “bag-of-bags-of-words”. Developing the previous integral we obtain:
 (4)
(4)
In Figure 1 we report the graphical representation of the DCM model. From another point of view, each Multinomial is linked to specific sub-topics and makes, for a specific document, the emission of some words more likely than others. Instead the Dirichlet represents a general topic that compounds the set of documents and thus the DCM could be also described as “bag-of-scaleddocuments”. The added value of the DCM approach consists in the ability to handle the “burstiness” of a rare word without introducing heuristics [13]. In fact, if a rare word appears once along a text, it is much more likely to appear again.
When we consider the entire set of documents , where each document is independent and identified by its count vector,
, where each document is independent and identified by its count vector,  , the likelihood of the
, the likelihood of the

Figure 1. Hierarchical representation of DCM model.
whole documents set (D) is
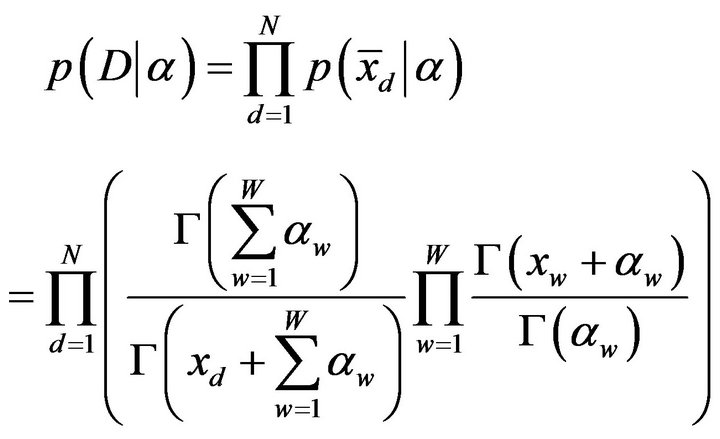 (5)
(5)
where xd is the sum of the counts of each word in the document d-th (åxdw) and xdw the count of word w-th for the document d-th. Thus the log-likelihood is:
 (6)
(6)
The parameters can be estimated by a fixed-point iteration scheme, as described in Section 4.
3. A Semantic-Based DCM
As explained in Section 2, we have a coefficient aw for each word compounding the vocabulary of the set of documents which is called “corpus”. The DCM model can be seen as a “bag-of-scaled-documents” where the Dirichlet takes into account a general topic and the Multinomial some specific sub-topics. Our aim in this contribution is to build a framework that allows us to insert specifically the topics (known or unknown) that compound the document, without losing the “burstiness” phenomenon and the classification performance. Thus we introduce a method to link the a coefficients to the hypothetic topics, indicated with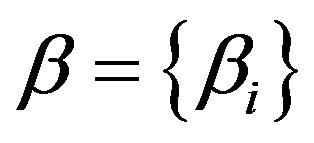 , by means of a function
, by means of a function 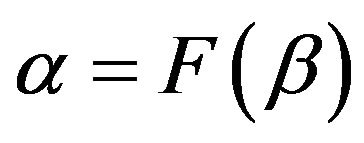 which must be positive in b since the Dirichlet coefficients are positive. Note that usually
which must be positive in b since the Dirichlet coefficients are positive. Note that usually  and, therefore, our proposed approach is parsimonious. Substituting the new function into the integral in Equation (1), the new model is:
and, therefore, our proposed approach is parsimonious. Substituting the new function into the integral in Equation (1), the new model is:
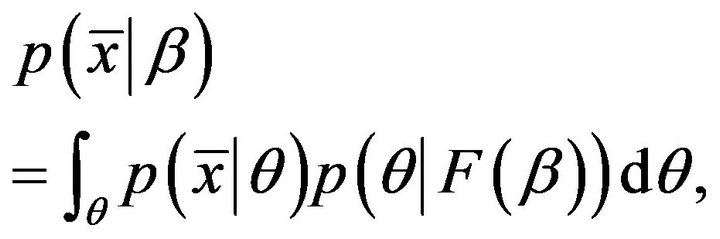 (7)
(7)
We have considered as function F(b) a linear combination based on a matrix D and the vector . D contains information about the way of splitting among topics the observed count vectors of the words contained in a diagonal matrix A and
. D contains information about the way of splitting among topics the observed count vectors of the words contained in a diagonal matrix A and  is a vector of coefficient (weights) for the topics. More specifically we assume that:
is a vector of coefficient (weights) for the topics. More specifically we assume that:
 (8)
(8)
 (9)
(9)
Note that:
•  with T the number of Topics;
with T the number of Topics;
• 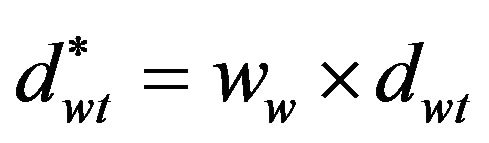 ;
;
• 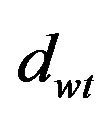 is the coefficient for word w-th used to define the degree of belonging to topic t-th and by which a portion of the count of word w-th is assigned to that particular topic t-th.
is the coefficient for word w-th used to define the degree of belonging to topic t-th and by which a portion of the count of word w-th is assigned to that particular topic t-th.
By substituting this linear combination into Equation (4), we obtain the same distribution but with the above mentioned linear combination for each a:

(10)
This model is a modified version of the DCM, henceforth semantic-based DCM (sbDCM), and the new loglikelihood for the set of documents becomes:
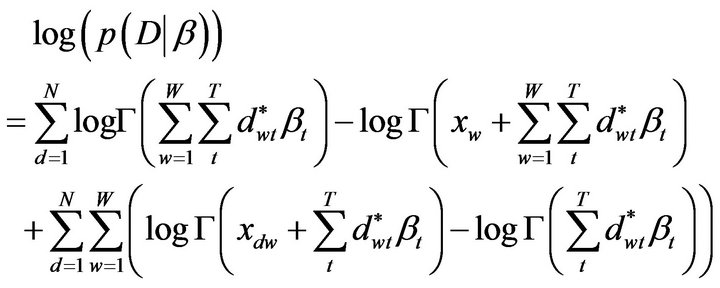 (11)
(11)
In Figure 2 we report the graphical representation of the new model where the a’s are substituted by a function of the b’s. An important aspect of the proposed approach is represented by the number T of topics to be inserted into the sbDCM that can be:
• Unknown, thus to be estimated on the basis of the available data.

Figure 2. Hierarchical representation of sbDCM model.
• A priori known (i.e. fixed by field experts).
The first case will be treated in Section 5.1, in particular since it is not always possible to know in advance the number of latent topics present in a corpora, it becomes very useful to build a statistical methodology for discovering efficiently and consistently a suitable number of topics. In this case the number of topics T can be considered a random variable. Thus, we use a segmentation procedure to group the words in order to create groups of words sharing common characteristics that can be considered as latent topics. The analysis is completed by choosing the best number of groups and a distance matrix is used to set the membership percentage (dwt) of each word to each latent topic. The second case will be treated in Section 5.2 and proposes to exploit the sbDCM model by employing a priori knowledge based on ontological schemas that describe the relations among concepts with regards to the general topics of the corpora. The ontology structure provides the set of relations among the concepts to which can be associated a certain number of key words, by a field expert(s). Thus, we want to use the classes of a given ontology and the associated key words to define in advance the number T of topics.
4. Parameters Estimation
There are several methods to maximize the log-like- lihood and to find the parameters associated with a DCM: simplified Newton iteration, the Expected Maximization method and the maximization of the simplified likelihood (called “leave-one-out” likelihood, LOO). Among them, the most general and flexible algorithm is the Expected Maximization (EM). The EM algorithm is an iterative procedure able to compute the maximum-likelihood estimates whenever data are incomplete or they are considered complete but not observable (latent variables) [14].
In general, considering 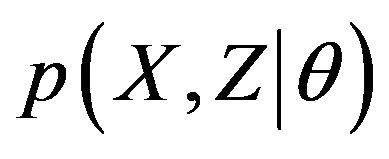 the joint probability distribution (or probability mass function) where X is the incomplete (but observable) data set and Z the missing (or latent) data, we can calculate the complete maximum likelihood estimation of model parameters q by means of the EM algorithm. We obtain an overall complexity reduction for what concerns the calculation of observed maximum-likelihood (ML) estimates. The goal is achieved by alternating the expectation (E-step) of the likelihood with the latent variables as if they are observed and the maximization (M-step) of the likelihood function found in the E-step. With the result of the M-step we update the new parameters qnew that are used again in the cycle, by starting from the E-step, until we reach a fixed degree of approximation e of the observed likelihood which increases step by step moving towards the maximum (that could be local) [15]. The EM can be built in different ways. One possibility is to see the EM as a lower bound maximization where we alternate the E-step to calculate an approximation of the lower bound for the log-likelihood and maximize it in the M-step until a stationary point (zero gradient) is reached. If we are able to find a lower bound for the log-likelihood we can maximize it via a fixed-point iteration; in fact it is the same principle of considering the EM as a lower bound maximization. In our context, for the DCM, the lower bound with
the joint probability distribution (or probability mass function) where X is the incomplete (but observable) data set and Z the missing (or latent) data, we can calculate the complete maximum likelihood estimation of model parameters q by means of the EM algorithm. We obtain an overall complexity reduction for what concerns the calculation of observed maximum-likelihood (ML) estimates. The goal is achieved by alternating the expectation (E-step) of the likelihood with the latent variables as if they are observed and the maximization (M-step) of the likelihood function found in the E-step. With the result of the M-step we update the new parameters qnew that are used again in the cycle, by starting from the E-step, until we reach a fixed degree of approximation e of the observed likelihood which increases step by step moving towards the maximum (that could be local) [15]. The EM can be built in different ways. One possibility is to see the EM as a lower bound maximization where we alternate the E-step to calculate an approximation of the lower bound for the log-likelihood and maximize it in the M-step until a stationary point (zero gradient) is reached. If we are able to find a lower bound for the log-likelihood we can maximize it via a fixed-point iteration; in fact it is the same principle of considering the EM as a lower bound maximization. In our context, for the DCM, the lower bound with 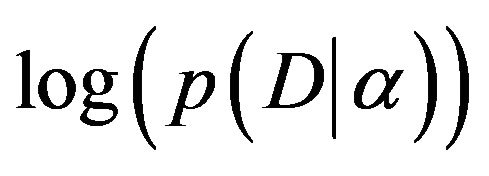 is the following quantity:
is the following quantity:
 (12)
(12)
this allows us to use a fixed point iteration whose steps are:
 (13)
(13)
where xd is the sum of the counts of each word in the document d-th , xdw the count of word w-th for the document d-th and
, xdw the count of word w-th for the document d-th and  the Dirichlet coefficient for word w at the k-th step. The algorithm is stopped when a degree of approximation e is reached. The iteration starts with aw equals to the occurrence percentage of the word w-th in the corpus. The estimated parameters, as said before, have an important characteristic: they follow the “burstiness” phenomenon of words. In fact the smaller aw is, the more “burstiness” effect is contained within a word, as revealed in Section 5.
the Dirichlet coefficient for word w at the k-th step. The algorithm is stopped when a degree of approximation e is reached. The iteration starts with aw equals to the occurrence percentage of the word w-th in the corpus. The estimated parameters, as said before, have an important characteristic: they follow the “burstiness” phenomenon of words. In fact the smaller aw is, the more “burstiness” effect is contained within a word, as revealed in Section 5.
In the case of sbDCM by considering the new loglikelihood, Equation (11), we can use the same lower bound employed before. The only modification lays on the substitution of the a coefficients with the linear function of b, as in Equation (9), and thereby the new fixed point iteration step is:
 (14)
(14)
As before we stop the iteration at a fixed degree of approximation and the coefficients dwt are those described in Section 3. The new a’s maintain the words burstiness, as we shall show in Section 5 and they are used to classify the document by employing a Naive Bayes classifier. For our applications, in the next section we have used for both models a value of e of 10−10. The iteration starts with bt equals to the percentage of each single cluster obtained by the grouping analysis of vocabulary words.
5. Model Performance
In this section we describe the evaluation of the different classifiers by using the parameters estimated from the DCM distribution. Thus, our training data set is compound of 6436 documents with a vocabulary (already filtered and stemmed) of 15,655 words so we have to estimate 15,655 a parameters. The a parameter is able to model the “burstiness” of a word. In fact, the smaller the a parameters are, the more bursty the emission of words is. This phenomenon is characteristic of rare words, therefore a coefficients are, on average, smaller for less counted words. The average value of the overall a parameters is 0.0342, the standard deviation is 0.1087 and the maximum and minimum values are respectively 6.6074 and 0.0025. Once the coefficient vector of a’s is obtained we employ seven different classifiers, three of which are described in [13] (normal (N), complement (C) and mixed (M). The remaining ones are proposed as the appropriate combination of the previous ones, in order to improve their characteristics. Those new classifiers are set in function of the number of words that a test-document has in common with the set of documents that compound a class; in this way we create a classifier in function of the number of words in common. Thus we analyze the following additional classifiers: COMPLEMENT + MIXED + NORMAL (CMN), COMPLEMENT + NORMAL (CN), COMPLEMENT + MIXED (CM), MIXED + NORMAL (MN).
In order to evaluate the classification performance we employ three performance indexes:
• Ind1: The proportion of true positive over the total number of test-documents:
• 
• Ind2: The proportion of classes that we are able to classify:
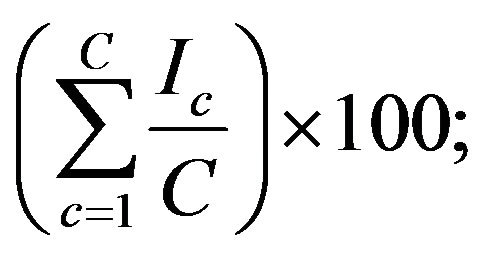
where Ic is an indicator that we set 1 if at least one document of the class is classified correctly, otherwise we set 0.
• Ind3: The proportion of true positive within each class over the number of test documents present in the class:

where Mc is the number of test-documents in each class, TPc is the number of true positive in the class and C the number of topics (46).
For the four combined classifiers such indexes have been calculated by varying the number of words in common between the test document and the class. In particular for our test we have used three different thresholds for the number of words (n): 15, 10 and 5. For example, we indicate with the initials CMn the classification rule that employs classifier C when the number of common words are less or equal to n and classifier M when the number of words in common is more than n. Instead, the initial CMNn.m identifies the using of classifier C until n, the classifier N over m and the classifier M between n and m. For the data at hand the number of words in common between the two sets (training and evaluation set) varies between 1 and 268. The above mentioned combination is based on the following idea: if the number of words in common between the bag of words and the correct class is low, then the most information content is in the complement set. Otherwise the needed information is contained either in the normal set or in the complement one. Taking into account such consideration we have set up different combination and we concluded that the useful trade-off among classifiers is equal to 10 (Table 1).
As we can see the best classifiers are the mixed and the CM10 ones. They are able to classify respectively 1237 and 1238 over 1609 documents that are distributed not uniformly among classes (46). These classifiers are able to classify at least a document per class even if there are classes containing only 2 documents. Between them the CM10 classifier has index three slightly better than mixed one. The worse classifier, in this case, is the complement version alone.

Table 1. Classification results by varying cluster numbers and using matrix C.
We now verify the goodness of the sbDCM models described in Section 3, to understand if we can insert latent topics into DCM by maintaining the burstiness and the same classification performance. Two kinds of matrixes have been used in the cluster procedure. One matrix contains the correlations among words C in the vocabulary and another G is constructed by calculating the Kruskal-Wallis index on the count matrix among words. The latter index g is defined as follows:
 (15)
(15)
where ni is the number of sample data, N the total observation number of the k samples, k the number of samples to be compared and  the mean rank of i-th group. The denominator of the index g is a correction factor needed when tied data are present in the data set, where p is the number of recurring ranks and ci is the times the i-th rank is repeated. The index g depends on the differences among the averages of the groups
the mean rank of i-th group. The denominator of the index g is a correction factor needed when tied data are present in the data set, where p is the number of recurring ranks and ci is the times the i-th rank is repeated. The index g depends on the differences among the averages of the groups 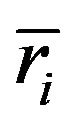 and the general average. If the samples come from the same population or from populations with the same central tendency, the arithmetic averages of the ranks of each group
and the general average. If the samples come from the same population or from populations with the same central tendency, the arithmetic averages of the ranks of each group
 should be similar to each other and to the general average
should be similar to each other and to the general average  as well. The training dataset contains 2051 documents with a vocabulary of 4096 words for both approaches. The evaluation dataset (again the same for both models) contains 1686 documents which are distributed over 46 classes. In Tables 1 and 2 we report the results from the two tests obtained respectively by matrixes C and G and by varying the number of groups in the cluster. In the tables we indicate with LLin the log-likelihood before the parameters updating and with LLout after the iteration procedure which is stopped when the error e = 10−10 is reached. The same with AICcin and AICcout that is the corrected Akaike Information Criterion (AICc) before and after the uploading. The indexes Ind1, Ind2 and Ind3 have been described in Section 5.1.
as well. The training dataset contains 2051 documents with a vocabulary of 4096 words for both approaches. The evaluation dataset (again the same for both models) contains 1686 documents which are distributed over 46 classes. In Tables 1 and 2 we report the results from the two tests obtained respectively by matrixes C and G and by varying the number of groups in the cluster. In the tables we indicate with LLin the log-likelihood before the parameters updating and with LLout after the iteration procedure which is stopped when the error e = 10−10 is reached. The same with AICcin and AICcout that is the corrected Akaike Information Criterion (AICc) before and after the uploading. The indexes Ind1, Ind2 and Ind3 have been described in Section 5.1.
As we can see in the two Tables 1 and 2, the percentages of correct classification (Ind1) are very close to the original ones with a parameter for each word (4096 parameters). Of course they depend on the type of classifier employed during the classification step. Considering both sbDCM and DCM, the differences produced by varying the number of groups are small. Moreover the AICc is always better in the new approach then considering each word as a parameter (DCM model). In particular for what concerns the approach based on the correlation matrix C (in Table 2) with 17 groups and on the Mixed classifier, it can predict correctly the 68.43% of documents. The log-likelihood and the AICc indexes along groups are quite similar, however the best value is obtained with 5 groups (respectively −205,412 and 410,834). Considering again the approach based on the correlation matrix C, we can conclude that, in terms of complexity expressed by the AIC index, the sbDCM approach whatever applied classifier is always better than the DCM. When we use matrix G (Table 2) the best classification performance is for the complement classifier based on 23 groups, with a percentage of 68.72%, a log-likelihood of −204,604, the AICc of 409,254. The best log-likelihood and AICc are for cluster with 46 groups (respectively −204,362 and 408,816). Even if the sbDCM distribution based on matrix G is not able to improve the classification performance of DCM, we can say that the sbDCM Index1 is always very close to the best one. In addition the new model is

Table 2. Classification results by varying cluster numbers and using matrix G.
always better in terms of either AIC and log-likelihood indexes. Moreover, if we perform an asymptotic chisquared test  considering the two cases (matrixes G and C) to decide whether the difference among loglikelihoods (LL), with respect to DCM, are significant (i.e. the difference is statistically meaningful if the
considering the two cases (matrixes G and C) to decide whether the difference among loglikelihoods (LL), with respect to DCM, are significant (i.e. the difference is statistically meaningful if the  is greater than 6), we can see from Tables 1 and 2 the test with matrix G has the best performance.
is greater than 6), we can see from Tables 1 and 2 the test with matrix G has the best performance.
Performance of the Semantic-Based Dirichlet Compound Multinomial with T Known in Advance
A different approach needs to be assessed when the number of available topic T is known in advance. In fact a text corpora could be enriched by several descriptions of treated topics according to the knowledge of field experts. In more details, the analysis could be provided with a priori knowledge based on ontological schemas that describe the relations among concepts with regards to the general topics of the corpora. An ontology (from which an ontological schema is derived) is a formal representation of a set of concepts within a domain and the relationships between those concepts [16]. It provides a shared vocabulary, which can be used to model a domain, that is, the type of objects and/or concepts that exist, and their properties and relations. In Figure 3 we report an example of graphical representation of an ontological schema. For example, if a text set deals with reputational risk management for corporate institutions, an ontology can be created on the basis of the four categories of problems (internal processes, people, systems and external events) defined by Basel II Accords.
Hence we can suppose that some specific sub-topics and key words, such as the possible causes of reputetional losses, will be almost surely treated along the texts.

Figure 3. Example of ontological schema.
Thereby, the ontology structure provides the set of relations among the concepts to which can be associated, by a field expert(s), a certain number of key words. Thus, we want to use the classes of a given ontology and the associated key words to define in advance the number T of topics. The ontological schema which we refer to, for the data at hand, deals with the so called reputational risk [17]. It is not simple to define and consequently to measure and to monitor the reputation concept since it involves intangible assets such as: honor, public opinion, perception, reliability, merit. By the way, it is a matter of fact, that a bad reputation can seriously affect and condition the performance of a company. Moreover companies tend to act once the adverse event has occurred. According to such approach we can say that there is not a risk management activity, but only a crisis management. With regards to reputational risk, media coverage plays a key role in determining a company’s reputation. This often occurs when a company reputation has been significantly damaged by unfair attacks from special interest groups or inaccurate reporting by the media. A detailed and structured analysis of what the media are saying is especially important because the media shape the perceptions and expectations of all the involved actors. Natural language processing technologies enable these services to scan a wide range of outlets, including newspapers, magazines, TV, radio, and blogs. In order to enable the application of the classification textual model sbDCM we have collaborated with the Italian market leader company in financial and economic communication, Sole24ORE. Sole- 24ORE team provided us with a set of 870 articles about Alitalia, an Italian flight company, covering a period of one year (Sept 07-Sept 08).
The 80% of the articles are used to train the model and the remaining 20% to validate the process. The objective is to classify the articles on the basis of the reputation ontology in order to understand the argument treated in the articles. The ontology classes used for the classification are:
• Identity: the perception that stakeholders have of the organization, person, product. It describes how the organization is perceived by the stakeholders.
• Corporate Image: the “persona” of the organitation. Usually for companies visibly manifested by way of branding and the use of trademarks and involves the mission and the vision. It involves brand value.
• Integrity: personal inner sense of “wholeness” deriving from honesty and consistent uprightness of character.
• Quality: the achievement or excellence of an entity. Quality is sometimes certificated by a third part.
• Reliability: ability of a system to perform/maintain its functions in routine and also in different hostile or/ and unexpected circumstances. It involves customer satisfaction and customer fidelitation.
• Social Responsibility: social responsibility is a doctrine that claims that an organization or individual has a responsibility to society. It involves foundation campaign and sustainability
• Technical Innovation: the Introduction of new technical products or services. Measure of the “RD orientation” of an organization (only for companies).
• Value For Money: the extent to which the utility of a product or service justifies its price.
Those classes define the concept of reputation of a company. To link the ontology classes to the textual analysis we use a set of key words for each class of the reputation schema. Since the articles are in Italian, the key words are in Italian as well. For example the concept of “Reliability” involves customer satisfaction and customer fidelitation and is characterized by the following set of key words: affidabilità, fiducia, consumatori, risorsa, organizzazione, commerciale, dinamicità, valore, mercato. On the basis of these key words, we perform a grouping analysis considering the 9 classes. From the clustering, we derive the matrix D. Empirical results show good performance in terms of correct classification rate. We obtain that, given 171 articles, we correctly classify the 68% of them.
6. Conclusions
This contribution has shown how to enrich the DCM model with a semantic extension. We also have proposed a method to insert latent topics within the “Dirichlet Compound Multinomial” (DCM) without losing the words “burstiness”: we call such a distribution “semanticbased Dirichlet Compound Multinomial” (sbDCM). The approaches assessed depend on the knowledge about the topics T. In fact there can be two alternative contexts: on one hand the topics are unknown in advanced, thus to be estimated on the basis of data at hand. On the other hand a text corpora could be enriched by several descriptions of treated topics according to the experience of the field expert(s). Specifically, the analysis can be empowered with a priori knowledge based on ontological schemas that describe the relations among concepts with regards to the general class argument of the corpora. In order to insert topics we create a new coefficient vector bt for each topic and later on we obtain the a parameters as a linear combination of them. The methodology is based on a matrix D containing the degree of membership of each word to a cluster (i.e. a topic) by using the cluster distance matrix. Then we split the words count vectors among latent topics and, by employing a fixed-point iteration, we generate the β coefficients representing the topics weights. In order to compare the two models DCM and sbDCM we have employed a “Naive Bayes Classifier” based on the estimated distributions as shown in [13]. Several classifiers have been proposed and tested, and among them the best performance is obtained by means of the “mixed formula” and “CM10”. Moreover, we run several tests to verify if the classification performance reached with an a for each word (DCM) is maintained or improved by the sbDCM.
Such an objective has been accomplished employing two different approaches. We propose two different methods to generate b parameters, one based on the correlation among words C and the second based on the Kruskal-Wallis index calculated on the words count matrix G. The results report that the test performances in terms of misclassification rate are quite close to each other and to the performance reached by the DCM. However the sbDCM distribution is able to obtain better results in terms of AIC and log-likelihood especially in the case of matrix G. Concluding, by using matrix D to describe how words count vectors can be split among topics, the b as weights for the topic and a as a linear combination we are able to obtain an optimal classification performance and to follow the burstiness.
7. Acknowledgements
This work has been supported by MUSING 2006 contract number 027097, 2006-2010 and FIRB, 2006-2009). The paper is the result of the close collaboration between the authors, however the paper has been written by Paola Cerchiello under the supervision of Paolo Giudici.