1. Introduction
In this paper, we consider queueing problems of allocating positions in a queue to agents, each of whom has a constant unit waiting cost, with monetary transfers. Examples of such problems are the use of large-scaled experimental installations, event sites, and so forth1.
Strategy-proofness is a standard property for nonmanipulability: The truthful revelation is a weakly dominant strategy for each agent. However, the strategyproof mechanism might have a Nash equilibrium which induces a non-optimal outcome. This problem is solved by secure implementation (Saijo, et al. [2]), that is, double implementation in dominant strategy equilibria and Nash equilibria2. Previous studies illustrate how difficult it is to find desirable and securely implementable social choice functions: Voting environments (Saijo, et al. [2]; Berga and Moreno [4]), public good economies (Saijo, et al. [2]; Nishizaki [5]), pure exchange economies (Mizukami and Wakayama [6]; Nishizaki [7]), the problems of providing a divisible and private good with monetary transfers (Saijo, et al. [2]; Kumar [8]), the problems of allocating indivisible and private goods with monetary transfers (Fujinaka and Wakayama [9]), Shapley-Scarf housing markets (Fujinaka and Wakayama [10]), and allotment economies with single-peaked preferences (Bochet and Sakai [11]).
This paper is most closely related to the one written by Fujinaka and Wakayama [9]. They show a constancy result on secure implementation when the domain satisfies minimal richness (Fujinaka and Wakayama [9]). Our model is a special case of their one and have many reasonable domains which do not satisfy minimal richness. On the basis of this fact, we study the possibility of secure implementation in queueing problems. Unfortunately, our main result shows that only constant social choice functions satisfy strategy-proofness and strong non-bossiness (Ritz [12]), both of which are necessary for secure implementation, on the domains satisfy weak indifference, which is weaker than minimal richness, introduced in this paper.
This paper is organized according to the following sections. In Section 2, we introduce our model, properties of social choice functions, and domain-richness conditions. We show our results in Section 3. Section 4 concludes this paper.
2. Notation and Definitions
Let be a set of agents. Let
be a set of agents. Let  be a queue, where, for each
be a queue, where, for each ,
,  is the position for agent
is the position for agent  in the queue
in the queue  and for each
and for each  with
with  For each
For each , let
, let 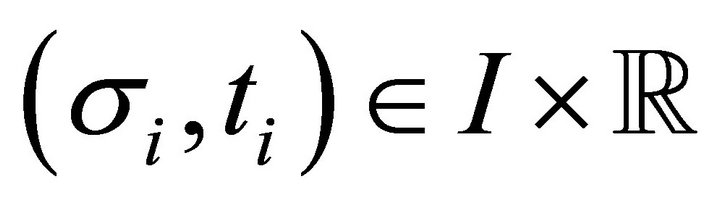 be a consumption bundle for agent
be a consumption bundle for agent , where
, where  is a monetary transfer for agent
is a monetary transfer for agent . Let
. Let  be a profile of monetary transfers and
be a profile of monetary transfers and  be a profile of consumption bundles, called an allocation. Let
be a profile of consumption bundles, called an allocation. Let

be the set of feasible allocations.
For each , let
, let  be a unit waiting cost for agent
be a unit waiting cost for agent  and
and  be a set of unit waiting costs for agent
be a set of unit waiting costs for agent . For each
. For each , let
, let  be the utility function for agent
be the utility function for agent  such that for each
such that for each  and each
and each ,
,

Let  be the domain and
be the domain and  be a profile of unit waiting costs. For each
be a profile of unit waiting costs. For each , let
, let  be a profile of unit waiting costs for agents other than agent
be a profile of unit waiting costs for agents other than agent .
.
Let  be a social choice function. For each
be a social choice function. For each , let
, let  be the allocation associated with the social choice function
be the allocation associated with the social choice function  at the profile of unit waiting costs
at the profile of unit waiting costs  and
and  be the consumption bundle for agent
be the consumption bundle for agent 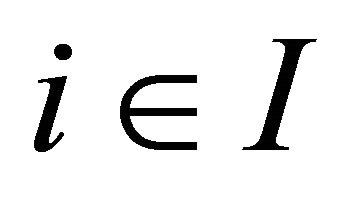 in the allocation
in the allocation .
.
Saijo et al. [2] show that strategy-proofness and strong non-bossiness are necessary for secure implementation.
Definition 1 The social choice function  satisfies strategy-proofness if and only if for each
satisfies strategy-proofness if and only if for each  and each
and each ,
,

Definition 2 The social choice function  satisfies strong non-bossiness if and only if for each
satisfies strong non-bossiness if and only if for each  and each
and each , if
, if

then 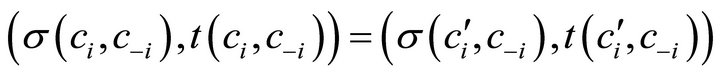
Fujinaka and Wakayama [9] show a constancy result on secure implementation when the domain satisfies minimal richness.
Definition 3 The domain  satisfies minimal richness if and only if for each
satisfies minimal richness if and only if for each , each
, each , each
, each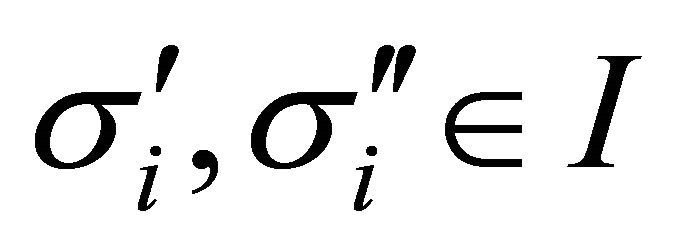 , and each
, and each 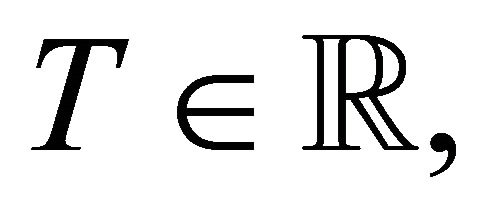 if
if  , then there exists
, then there exists  such that 1)
such that 1)  and 2)
and 2)  for each
for each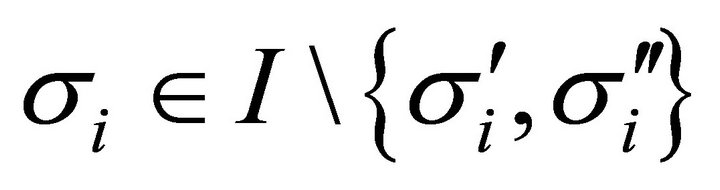 .
.
The following example shows that many reasonable domains do not satisfy minimal richness in our model.
Example 1 Let  and
and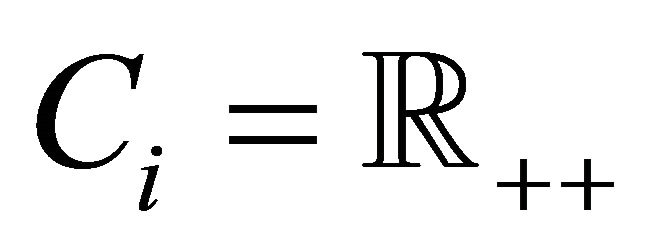 . Moreover, let
. Moreover, let . In this case, we have
. In this case, we have . Let
. Let  be such that
be such that , that is,
, that is, . This implies that condition 1) in Definition 3 holds. On the other hand, if
. This implies that condition 1) in Definition 3 holds. On the other hand, if , then
, then  for
for . This implies that condition 2) in Definition 3 does not hold.
. This implies that condition 2) in Definition 3 does not hold.
Our main result implies a constancy result on secure implementation when the domain satisfies weak indifference which is weaker than minimal richness.
Definition 4 The domain  satisfies weak indifference if and only if for each
satisfies weak indifference if and only if for each , each
, each , each
, each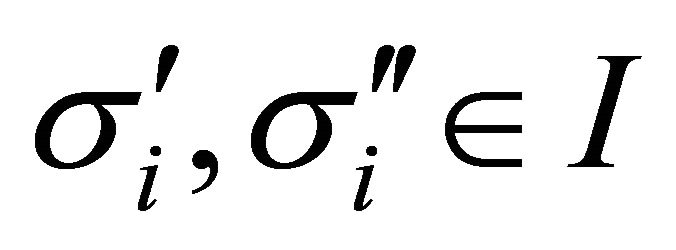 , and each
, and each , if
, if , then there exists
, then there exists  such that
such that

Remark 1 In our model, weak indifference is equivalent to convexity3.
3. Results
For simplicity of notation, let ,
,  ,
,  ,
,  ,
,  and
and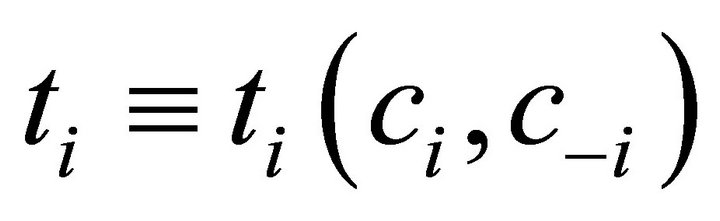 ,
,  ,
,  ,
, 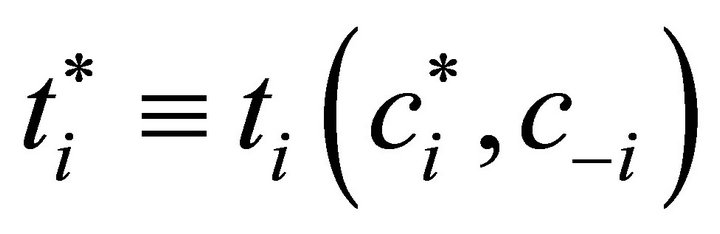 ,
,  for each
for each  and each
and each .
.
3.1. Preliminary Results
In this subsection, we assume that the social choice function  satisfies strategy-proofness.
satisfies strategy-proofness.
Lemma 1 shows that each agent’s monetary transfer depends on her position in the queue given unit waiting costs for other agents. Since the proof is similar to Fujinaka and Wakayama [9], it is omitted.
Lemma 1 For each  and each
and each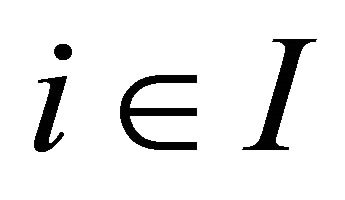 , if
, if , then
, then .
.
Lemma 2 shows that if there exists a unit waiting cost such that some two different consumption bundles are indifferent in terms of utility level, then the position associated with the unit waiting cost is in between the two positions. In Lemma 2, we use the following notation: for each , each
, each , each
, each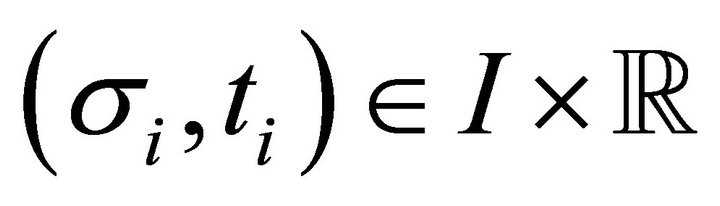 , and each
, and each , let
, let .
.
Lemma 2 For each 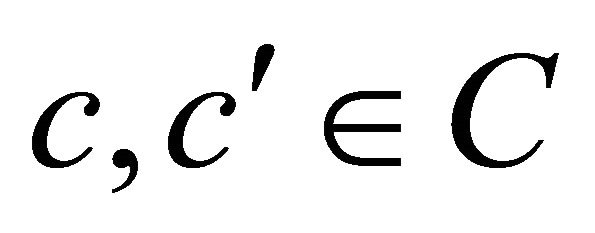 and each
and each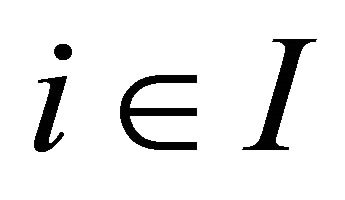 , if
, if  and there exists
and there exists  such that
such that , then
, then .
.
Proof. Suppose, by contradiction, that there exist  and
and  such that
such that ,
,  for some
for some , and
, and  or
or . We consider the case of
. We consider the case of . By the hypothesis, we have
. By the hypothesis, we have
 (1)
(1)
By the definition of , we have
, we have
 (2)
(2)
By the definition of  and strategy-proofness, we have
and strategy-proofness, we have
 (3)
(3)
By Equations (1)-(3) and , we have
, we have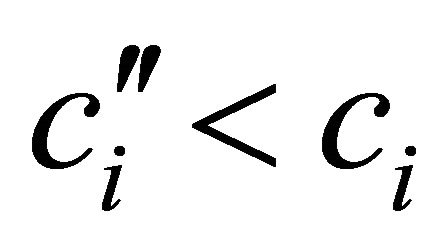 . Since we consider the case of
. Since we consider the case of , this implies
, this implies
 (4)
(4)
By the definition of  and strategy-proofness, we have
and strategy-proofness, we have . This is a contradiction to Equation (4). Similarly, we have a contradiction to strategy-proofness in the case of
. This is a contradiction to Equation (4). Similarly, we have a contradiction to strategy-proofness in the case of . ■
. ■
3.2. Main Result
Theorem 1 Suppose that the domain  satisfies weak indifference. The social choice function
satisfies weak indifference. The social choice function  satisfies strategy-proofness and strong non-bossiness if and only if it is constant5.
satisfies strategy-proofness and strong non-bossiness if and only if it is constant5.
Proof. Since the “if” part is obvious, we only prove the “only if” part. Let . Firstly, we show
. Firstly, we show  for each
for each . Suppose, by contradiction, that there exists
. Suppose, by contradiction, that there exists 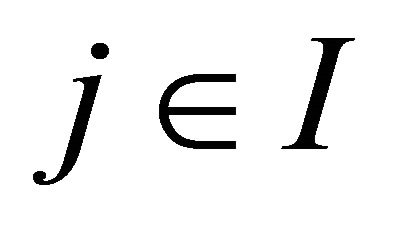 such that
such that  . By strong non-bossiness and strategy-proofness, this implies
. By strong non-bossiness and strategy-proofness, this implies
 (5)
(5)
By Lemma 1, this implies  or
or . Since
. Since , by strong non-bossiness and strategy-proofness, it also implies
, by strong non-bossiness and strategy-proofness, it also implies
 (6)
(6)
By Equations (5) and (6), we have  . Since
. Since  satisfies weak indifference, this implies that there exists
satisfies weak indifference, this implies that there exists  such that
such that
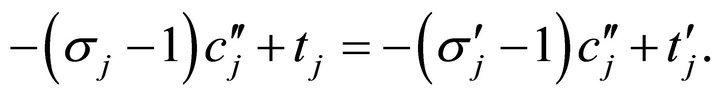 (7)
(7)
We consider the case of . In this case, by Lemma 2, we have
. In this case, by Lemma 2, we have . If
. If  or
or , then, by Equation (7) and strong nonbossiness, we have
, then, by Equation (7) and strong nonbossiness, we have . This is a contradiction. Therefore, we know
. This is a contradiction. Therefore, we know

By applying the above argument to the left inequality repeatedly, we can find  such that
such that 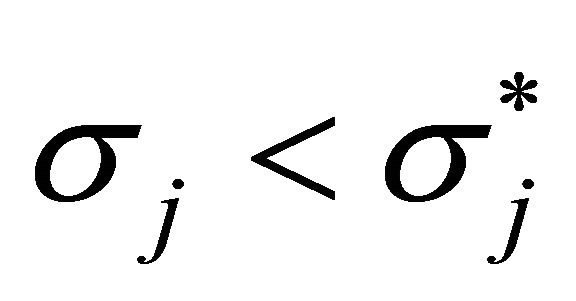 and
and , where there exists no position between
, where there exists no position between  and
and  induced by a unit waiting cost for agent
induced by a unit waiting cost for agent  given
given . In this case, we have
. In this case, we have . By strong non-bossiness, these imply
. By strong non-bossiness, these imply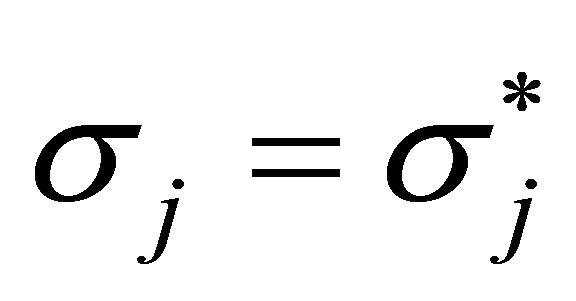 . This is a contradiction. Similarly, we have a contradiction in the case of
. This is a contradiction. Similarly, we have a contradiction in the case of .
.
Without loss of generality, let . Therefore, we have
. Therefore, we have
 (8)
(8)
By the same argument stated above, we also have
 (9)
(9)
where  is a profile of unit waiting costs for agents other than agents 1 and 2. By Equations (8) and (9), we have
is a profile of unit waiting costs for agents other than agents 1 and 2. By Equations (8) and (9), we have
 .
.
By sequentially replacing  by
by  for each
for each  in this manner, we finally prove
in this manner, we finally prove  . ■
. ■
Remark 2 The above theorem does not depend on the finiteness of the number of positions, which is used to prove Claim 3 in Proposition 1 of Fujinaka and Wakayama [9].
Obviously, constant social choice functions are securely implementable. Therefore, by bringing the above theorem together with a characterization of securely implementable social choice functions by Saijo et al. [2], we have the following constancy result on secure implementation.
Corollary 1 Suppose that the domain satisfies weak indifference. The social choice function is securely implementable if and only if it is constant.
Remark 3 In our model, Maskin monotonicity is not stronger than strategy-proofness6. This relationship implies that our main result is established by secure implementability but not by Nash implementability.
Remark 4 Saijo [14] shows the following constancy result on “Nash” implementation: The social choice function satisfies Maskin monotonicity and dual dominance (Saijo [14]) if and only if it satisfies constancy. In line with such domination, Fujinaka and Wakayama [9] show the following constancy result on “secure” implementation: The securely implementable social choice function satisfies non-dominance (Fujinaka and Wakayama [9]) if and only if it satisfies constancy. Note that nondominance is weaker than dual dominance7. In our model, similar to the relationship between minimal richness and weak indifference, we have a constancy result on secure implementation by a weaker condition than non-dominance as follows: for each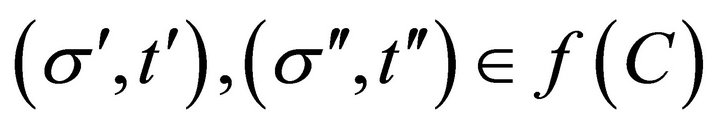 , each
, each  such that
such that  and
and , and each
, and each , if there exists no
, if there exists no  such that
such that  and
and
 , then there exists
, then there exists  such that
such that , where
, where

for each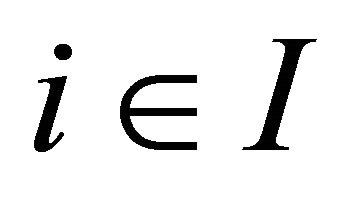 , each
, each 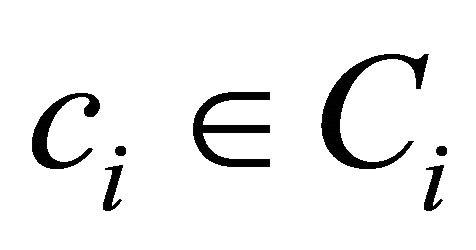 and each
and each .
.
4. Conclusion
This paper studies secure implementability in queueing problems. Fujinaka and Wakayama [9] show a constancy result on secure implementation. Our model is a special case of their one and have many reasonable domains which do not satisfy minimal richness. However, we have the same constancy result under less restrictive domain-richness conditions. On the other hand, it remains to show domain-richness conditions for the existence of non-constant securely implementable social choice functions. However, our main result implies that it is difficult to find such conditions that are reasonable in the economic sense.
5. Acknowledgements
This paper is based on my M.A. thesis presented to the Graduate School of Economics, Osaka University. The author would like to thank an anonymous referee, Tatsuyoshi Saijo, Masaki Aoyagi, Yuji Fujinaka, Kazuhiko Hashimoto, Shuhei Morimoto, Shinji Ohseto, Shigehiro Serizawa, Takuma Wakayama, and seminar participants at the 2008 Japanese Economic Association Spring Meeting, Tohoku University, for their helpful comments. The author is especially grateful to Tatsuyoshi Saijo, Yuji Fujinaka, and Takuma Wakayama for their valuable advices. The author acknowledges for the Global COE program of Osaka University for the financial supports. The responsibility for any errors that remain is entirely the author.
NOTES
2This concept is considered to be a benchmark for constructing mechanisms which work well in laboratories. See Cason, et al. [3] for experimental results.
3For the relationship among weak indifference and certain domainrichness conditions, see Appendix in Nishizaki [13].
4Note that the equality does not hold. If it holds, then we have  by Equations (1) and (2). This implies that f should be a correspondence since we consider the case of
by Equations (1) and (2). This implies that f should be a correspondence since we consider the case of .
.
5For the tightness of this theorem, see Examples 2, 3, and 4 in Nishizaki [13].
6For this relationship, see Remark 6 in Nishizaki [13].
6For the relationship among dual dominance, non-dominance, and secure implementability, see the supplementary note provided by Fujinaka and Wakayama [9] available online at: http://www.iser.osakau.ac.jp/library/dp/2007/DP0699N.pdf