Estimators of Linear Regression Model and Prediction under Some Assumptions Violation ()
1. Introduction
Linear regression model is probably the most widely used statistical technique for solving functional relationship problems among variables. It helps to explain observations of a dependent variable, y, with observed values of one or more independent variables, X1, X2,  , Xp. In an attempt to explain the dependent variable, prediction of its values often becomes very essential and necessary. Moreover, the linear regression model is formulated under some basic assumptions. Among these assumptions are regressors being assumed to be non-stochastic (fixed in repeated sampling) and independent. The error terms also assumed to be independent, have constant variance and are also independent of the regressors. When all these assumptions of the classical linear regression model are satisfied, the Ordinary Least Square (OLS) estimator given as:
, Xp. In an attempt to explain the dependent variable, prediction of its values often becomes very essential and necessary. Moreover, the linear regression model is formulated under some basic assumptions. Among these assumptions are regressors being assumed to be non-stochastic (fixed in repeated sampling) and independent. The error terms also assumed to be independent, have constant variance and are also independent of the regressors. When all these assumptions of the classical linear regression model are satisfied, the Ordinary Least Square (OLS) estimator given as:
 (1)
(1)
is known to possess some ideal or optimum properties of an estimator which include linearity, unbiasedness and efficiency [1]. These had been summed together as Best Linear Unbiased Estimator (BLUE). However, these assumptions are not satisfied in some real life situation. Consequently, various methods of estimation of the model parameters have been developed.
The assumption of non-stochastic regressors is not always satisfied, especially in business, economic and social sciences because their regressors are often generated by stochastic process beyond their control. Many authors, including Neter and Wasserman [2], Fomby et al. [3], Maddala [4] have given situations and instances where this assumption may be violated and have also discussed its consequences on the OLS estimator when used to estimate the model parameters. They emphasized that if regressors are stochastic and independent of the error terms, the OLS estimator is still unbiased and has minimum variance even though it is not BLUE. They also pointed out that the traditional hypothesis testing remains valid if the error terms are further assumed to be normal. However, modification is required in the area of confidence interval calculated for each sample and the power of the test.
The violation of the assumption of independent regressors leads to multicollinearity. With strongly interrelated regressors, interpretation given to the regression coefficients may no longer be valid because the assumption under which the regression model is built has been violated. Although the estimates of the regression coefficients provided by the OLS estimator is still unbiased as long as multicollinearity is not perfect, the regression coefficients may have large sampling errors which affect both the inference and forecasting resulting from the model [5]. Various methods have been developed to estimate the model parameters when multicollinearity is present in a data set. These estimators include Ridge Regression estimator developed by Hoerl [6] and Hoerland Kennard [7], Estimator based on Principal Component Regression suggested by Massy [8], Marquardt [9] and Bock, Yancey and Judge [10], Naes and Marten [11], and method of Partial Least Squares developed by Hermon Wold in the 1960s [12-14].
The methodology of the biased estimator of regression coefficients due to principal component regression involves two stages. This two-stage procedure first reduces the predictor variables using principal component analysis and then uses the reduced variables in an OLS regression fit. While it often works well in practice, there is no general theoretical reason that the most informative linear function of the predictor variables should lie among the dominant principal components of the multivariate distribution of the predictor variables.
Consider the linear regression model,
 (2)
(2)
Let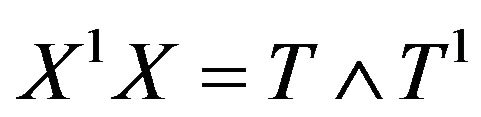 , where
, where  is a pxp diagonal matrix of the eignvalues of
is a pxp diagonal matrix of the eignvalues of  and T is a p × p orthogonal matrix whose columns are the eigenvectors associated with
and T is a p × p orthogonal matrix whose columns are the eigenvectors associated with . Then the above model can be written as:
. Then the above model can be written as:
 (3)
(3)
where 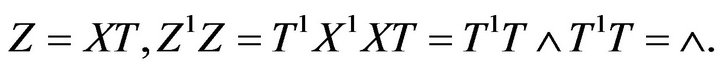
The columns of Z, which define a new set of orthogonal regressors, such as  are referred to as principle components. The principle components regression approach combats multicollinearity by using less than the full set of principle components in the model. Using all will give back into the result of the OLS estimator. To obtain the principle component estimator, assume that the regressors are arranged in order of descending eigen values,
are referred to as principle components. The principle components regression approach combats multicollinearity by using less than the full set of principle components in the model. Using all will give back into the result of the OLS estimator. To obtain the principle component estimator, assume that the regressors are arranged in order of descending eigen values,  and that the last of these eigen values are approximately equal to zero. In principal components regression, the principal components corresponding to near zero eigen values are removed from the analysis and the least squares applied to the remaining component.
and that the last of these eigen values are approximately equal to zero. In principal components regression, the principal components corresponding to near zero eigen values are removed from the analysis and the least squares applied to the remaining component.
When all the assumptions of the Classical Linear Regression Model hold except that the error terms are not homoscedastic  but are heteroscedastic
but are heteroscedastic , the resulting model is the Generalized Least Squares (GLS) Model. Aitken [15] has shown that the GLS estimator β of β given as
, the resulting model is the Generalized Least Squares (GLS) Model. Aitken [15] has shown that the GLS estimator β of β given as
 is efficient among the class of linear unbiased estimators of β with variance-covariance matrix of β given as
is efficient among the class of linear unbiased estimators of β with variance-covariance matrix of β given as where Ω is assumed to be known. The GLS estimator described requires Ω, and in particular ρ to be known before the parameters can be estimated. Thus, in linear model with autocorrelated error terms having AR(1):
where Ω is assumed to be known. The GLS estimator described requires Ω, and in particular ρ to be known before the parameters can be estimated. Thus, in linear model with autocorrelated error terms having AR(1):

and
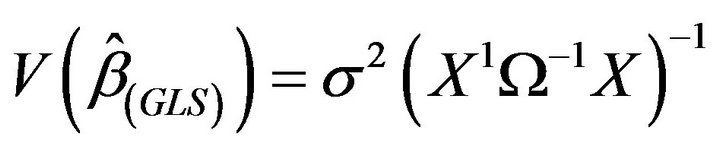 (4)
(4)
where

and , and the inverse of Ω is
, and the inverse of Ω is

Now with a suitable  xn matrix transformation
xn matrix transformation  defined by
defined by
 (5)
(5)
Multiplying then shows that  gives an n × n matrix which, apart from a proportional constant, is identical with
gives an n × n matrix which, apart from a proportional constant, is identical with  except for the first elements in the leading diagonal, which is
except for the first elements in the leading diagonal, which is  rather than unity. With another n × n transformation matrix P obtained from
rather than unity. With another n × n transformation matrix P obtained from 
by adding a new row with  in the first position and zero elsewhere, that is
in the first position and zero elsewhere, that is
 (6)
(6)
Multiplying shows that . The difference between
. The difference between  and P lies only in the treatment of the first sample observation. However, when n is large, the difference is negligible, but in small sample, the difference can be major. If Ω or more precisely ρ is known, the GLS estimation could be achieved by applying the OLS via the transformation matrix
and P lies only in the treatment of the first sample observation. However, when n is large, the difference is negligible, but in small sample, the difference can be major. If Ω or more precisely ρ is known, the GLS estimation could be achieved by applying the OLS via the transformation matrix  and P above. However, this is not often the case; we resort to estimating Ω to have a Feasible Generalized Least Squares Estimator. This estimator becomes feasible when ρ is replaced by a consistent estimator
and P above. However, this is not often the case; we resort to estimating Ω to have a Feasible Generalized Least Squares Estimator. This estimator becomes feasible when ρ is replaced by a consistent estimator  [3]. There are several ways of consistently estimating ρ, however, some of them either use the
[3]. There are several ways of consistently estimating ρ, however, some of them either use the  or P transformation matrix.
or P transformation matrix.
Several authors have worked on this violation especially in terms of the parameters’ estimation of the linear regression model with autoregressive of orders one. The OLS estimator is inefficient even though unbiased. Its predicted values are also inefficient and the sampling variances of the autocorrelated error terms are known to be underestimated causing the t and the F tests to be invalid [3-5] and [16]. To compensate for the loss of efficiency, several feasible GLS estimators have been developed. These include the estimator provided by Cochrane and Orcutt [17], Paris and Winstern [18], Hildreth and Lu [19], Durbin [20], Theil [21], the Maximum Likelihood and the Maximum Likelihood Grid [22], and Thornton [23]. Among others, the Maximum Likelihood and Maximum Likelihood Grid impose stationary by constraining the serial correlation coefficient to be between –1 and 1 and keep the first observation for estimation while that of Cochrane and Orcutt and Hildreth and Lu drops the first observation. Chipman [24], Kramer [25], Kleiber [26], Iyaniwura and Nwabueze [27], Nwabueze [28-30], Ayinde and Ipinyomi [31] and many other authors have not only examined these estimators but have also noted that their performances and efficiency depend on the structure of the regressor used. Rao and Griliches [32] did one of the earliest Monte-Carlo investigations on the small sample properties of several two-stage regression methods in the context of autocorrelated error terms. Other recent works done on these estimators and the violations of the assumptions of classical linear regression model include that of Ayinde and Iyaniwura [33], Ayinde and Oyejola [34], Ayinde [35], Ayinde and Olaomi [36], Ayinde and Olaomi [37] and Ayinde [38].
In spite of these several works on these estimators, none has actually been done on prediction especially as it relates multicollinearity problem. Therefore, this paper does not only examine the predictive ability of some of these estimators but also does it under some violations of assumption of regression model making the model much closer to reality.
2. Materials and Methods
Consider the linear regression model of the form:
 (7)
(7)
where  and
and  are stochastic and correlated.
are stochastic and correlated.
For Monte-Carlo simulation study, the parameters of equation (1) were specified and fixed as β0 = 4, β1 = 2.5, β2 = 1.8 and β3 = 0.6. The levels of intercorrelation (multicollinearity) among the independent variables were sixteen (16) and specified as:
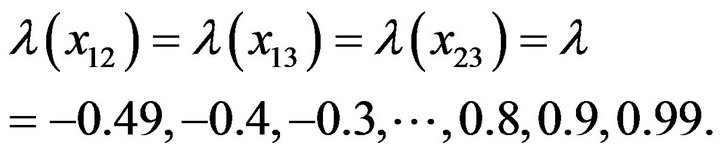
The levels of autocorrelation is twenty-one (21) and are specified as  Furthermore, the experiment was replicated in 1000 times
Furthermore, the experiment was replicated in 1000 times  under six (6) levels of sample sizes
under six (6) levels of sample sizes . The correlated stochastic normal regressors were generated by using the equations provided by Ayinde [39] and Ayinde and Adegboye [40] to generate normally distributed random variables with specified intercorrelation. With
. The correlated stochastic normal regressors were generated by using the equations provided by Ayinde [39] and Ayinde and Adegboye [40] to generate normally distributed random variables with specified intercorrelation. With , the equations give:
, the equations give:
 (8)
(8)
where  ,
,  and
and  ; and
; and 
By these equations, the inter-correlation matrix has to be positive definite and hence, the correlations among the independent variables were taken as prescribed earlier
 . In the study, we assumed
. In the study, we assumed
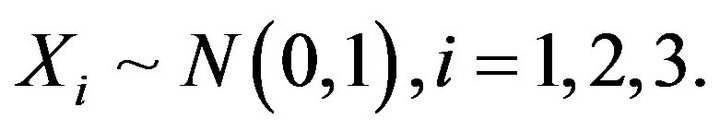
The error terms were generated using one of the distributional properties of the autocorrelated error terms
 and the AR(1) equation as follows:
and the AR(1) equation as follows:
 (9)
(9)
 (10)
(10)
Since some of these estimators have now been incorporated into the Time Series Processor (TSP 5.0) [41] software, a computer program was written using the software to examine the goodness of fit statistics of the estimators by calculating their Adjusted Coefficient of Determination of the model . The estimators are Ordinary Least Square (OLS), Cochrane Orcutt (COR), Maximum Likelihood (ML) and the estimator based on Principal Component (PC) Analysis.The two possible PCs (PC1 and PC2) of the Principal Component Analysis were used. The Adjusted Coefficient of Determination of the model was averaged over the numbers of replications. i.e.
. The estimators are Ordinary Least Square (OLS), Cochrane Orcutt (COR), Maximum Likelihood (ML) and the estimator based on Principal Component (PC) Analysis.The two possible PCs (PC1 and PC2) of the Principal Component Analysis were used. The Adjusted Coefficient of Determination of the model was averaged over the numbers of replications. i.e.
 (11)
(11)
An estimator is the best if its Adjusted Coefficient of Determination is the closest to unity.
3. Results and Discussion
The full summary of the simulated results of each estimator at different level of sample size, muticollinearity, and autocorrelation is contained in the work of Apata [42]. The graphical representations of the results when n = 10, 15, 20, 30, 50 and 100 are respectively presented in Figures 1, 2, 3, 4, 5 and 6.
From these figures, it is observed that the performances of COR at each level of multicollinearity and those of ML, especially when the sample size is large, over the levels of autocorrelation have a convex-like pattern, while those of OLS, PC1 and PC2 are generally concave-like. Also, as the level of multicollinearity increases the estimators, except PC estimators when multicolinearity is negative, rapidly perform better as their averaged adjusted coefficient of determination increases over the levels of autocorrelation. The PC estimators perform better as multicollinearity level increases in its

Figure 1. Predictive ability of the estimators at each level of multicollinearity and all levels of autocorrelation when n = 10.

Figure 2. Predictive ability of the estimators at each level of multicollinearity and all levels of autocorrelation when n = 15.
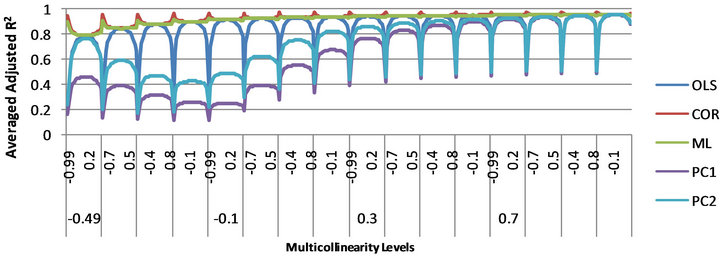
Figure 3. Predictive ability of the estimators at each level of multicollinearity and all levels of autocorrelation when n = 20.

Figure 4. Predictive ability of the estimators at each level of multicollinearity and all levels of autocorrelation when n = 30.

Figure 5. Predictive ability of the estimators at each level of multicollinearity and all levels of autocorrelation when n = 50.

Figure 6. Predictive ability of the estimators at each level of multicollinearity and all levels of autocorrelation when n = 100.
absolute value. The COR and ML estimators are generally good for prediction in the presence of multicollinearity and autocorrelated error term. However, at low levels of autocorrelation, the OLS estimator is either best or competes consistently with the best estimator, while the PC2 estimator is also either best or competes with the best when multicollinearity is high  .
.
Specifically, according to Figure 1 when n = 10, the average adjusted co-efficient of determination of the ML and COR estimators is often greater than 0.8. The OLS estimator consistently performs well and competes with the ML and COR estimators at low and occasionally at moderate levels of autocorrelation in all the levels of multicollinearity. Also, the PR1 and PR2 do perform well and compete with ML and COR except at high and very high level of autocorrelation when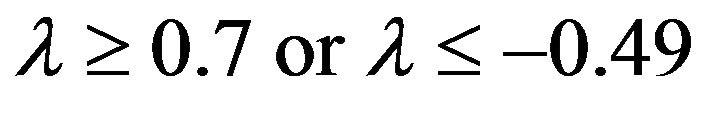 . The best estimator for prediction is summarized in Table 1.
. The best estimator for prediction is summarized in Table 1.


Table 1. The best estimator for prediction at different level of multicollinearity and autocorrelation when n = 10.
From Table 1, when n = 10, the COR estimator is best except when . At these instances, the PC2 estimator is often best when
. At these instances, the PC2 estimator is often best when  and
and  Moreover, when
Moreover, when 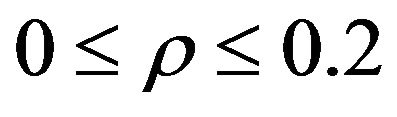 and
and , the OLS estimator is generally best. At other instances, the best estimator is frequently ML and very sparsely COR.
, the OLS estimator is generally best. At other instances, the best estimator is frequently ML and very sparsely COR.
When n = 15, Figure 2 reveals that the pattern of the results is not different from when n = 10 except that PR estimators now compete very well with the ML and COR when . The best estimator for prediction is presented in Table 2.
. The best estimator for prediction is presented in Table 2.
According to Table 2, the COR estimator is generally


Table 2. The best estimator for prediction at different level of multicollinearity and autocorrelation when n = 15.
best except when . At these instances, the PC2 estimator is best when
. At these instances, the PC2 estimator is best when  and at other instances, the best estimator is frequently ML or COR.
and at other instances, the best estimator is frequently ML or COR.
When n = 20, 30, 50 and 100, the results according to Figures 3, 4, 5 and 6 are not too different. However, from Table 3 when n = 20, the COR estimator is generally best except when . At these instances, the PC2 estimator is best when
. At these instances, the PC2 estimator is best when 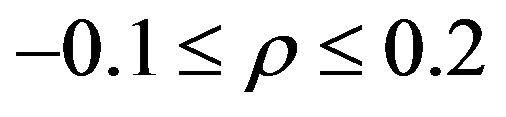 and
and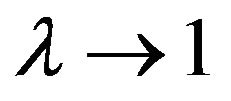 . At other instances, the ML or COR is best.
. At other instances, the ML or COR is best.
When n = 30 from Table 4, COR estimator is gener-
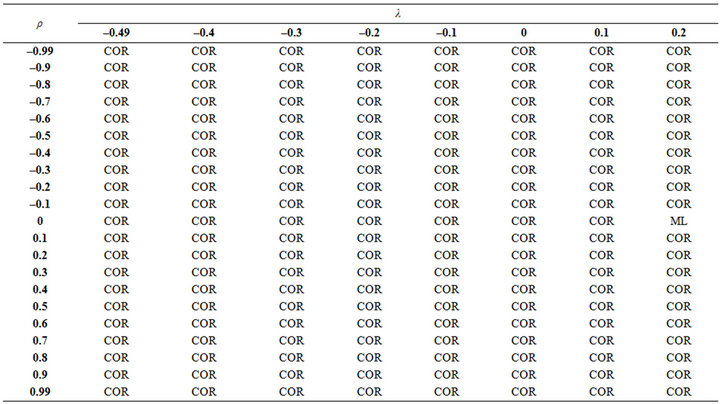

Table 3. The best estimator for prediction at different level of multicollinearity and autocorrelation when n = 20.


Table 4. The best estimator for prediction at different level of multicollinearity and autocorrelation when n = 30.
ally best except when . At these instances, the PC2 estimator is best when
. At these instances, the PC2 estimator is best when . At other instances, the best estimator is frequently ML and sparsely COR.
. At other instances, the best estimator is frequently ML and sparsely COR.
From Table 5 when n = 50, COR estimator is generally best except when . At these
. At these


Table 5. The best estimator for prediction at different level of multicollinearity and autocorrelation when n = 50.
instances, the PC2 estimator is best. When n = 100 from Table 6, COR estimator is generally best.
4. Conclusion
The performances COR, ML, OLS and PCs estimators in prediction have been critically examined under the violation of the assumptions of fixed regressors, independent regressors and error terms. The paper has not only generally revealed how the performances of these estimators are affected by multicollinearity, autocorrelation and sample sizes but has also specifically identified the best estimator for prediction purpose. The COR and ML are

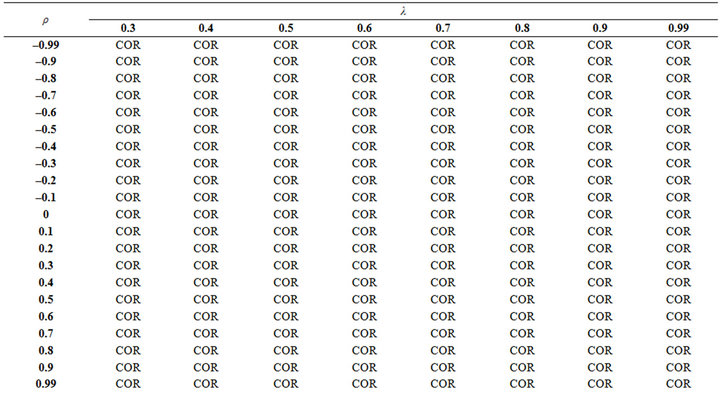
Table 6. The best estimator for prediction at different level of multicolli nearity and autocorrelation when n = 100.
generally best for prediction. At low levels of autocorrelation, the OLS estimator is either best or competes consistently with the best estimator while the PC2 estimator is either best or competes also with the best when multicollinearity level is high.