Some Properties of the Class of Univalent Functions with Negative Coefficients ()
1. Introduction
Let  be the class of analytic functions in the open unit disc
be the class of analytic functions in the open unit disc
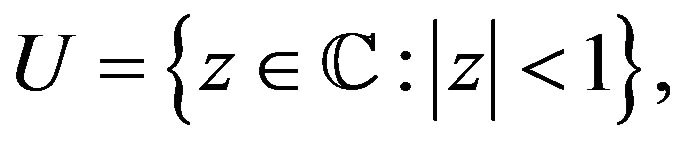
and 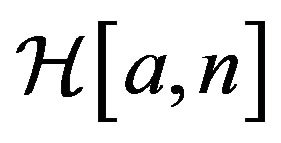 be the subclass of
be the subclass of  consisting of functions of the form
consisting of functions of the form
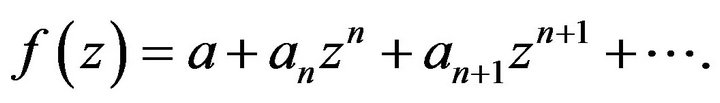
Let  denote the class of functions
denote the class of functions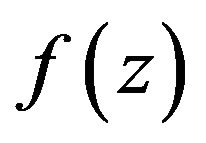 normalized by
normalized by
 (1)
(1)
which are analytic in the open unit disc. In particular,
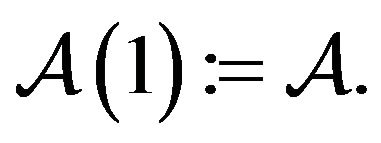
For two functions 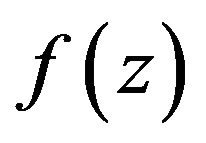 given by (1) and
given by (1) and  given by
given by

the Hadamard product (or convolution) 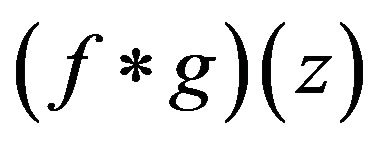 is defined, as usual, by
is defined, as usual, by
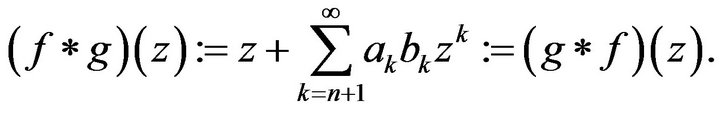
Let the function 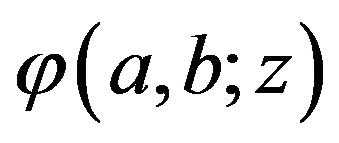 be given by:
be given by:

where  denotes the Pochhammer symbol (or the shifted factorial) defined by:
denotes the Pochhammer symbol (or the shifted factorial) defined by:
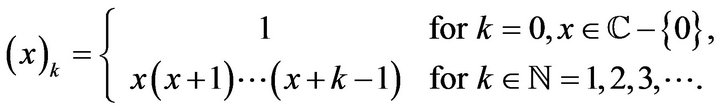
Carlson and Shaffer [1] introduced a convolution operator on  involving an incomplete beta function as:
involving an incomplete beta function as:
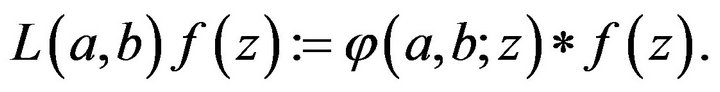 (2)
(2)
Our work here motivated by Catas [2], who introduced an operator on  as follows:
as follows:

where
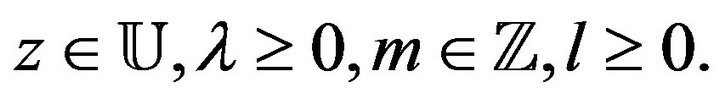
Now, using the Hadamard product (or convolution), the authors (cf. [3,4]) introduced the following linear operator:
Definition 1.1 Let

where

and 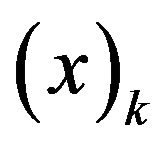 is the Pochhammer symbol. We defines a linear operator
is the Pochhammer symbol. We defines a linear operator 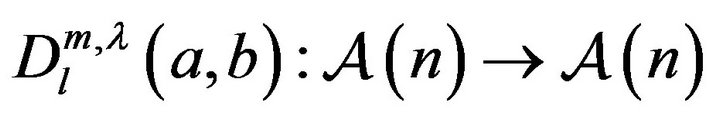 by the following Hadamard product:
by the following Hadamard product:
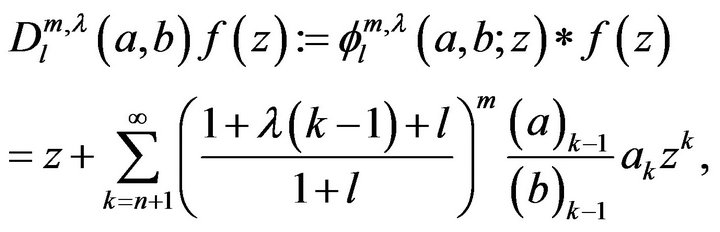 (3)
(3)
where

and  the Pochhammer symbol .
the Pochhammer symbol .
Special cases of this operator include:
• 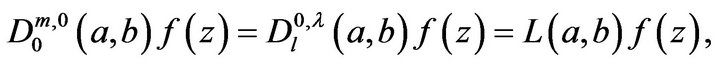 see [1].
see [1].
• the Catas drivative operator [2]: 
• the Ruscheweyh derivative operator [5] in the cases:
• 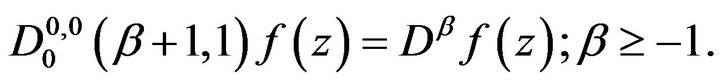
• the Salagean derivative operator [6]: 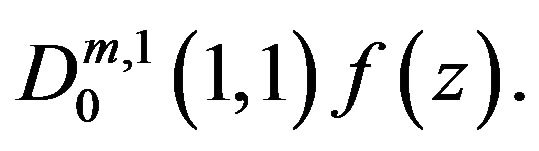
• the generalized Salagean derivative operator introduced by Al-Oboudi [7]: 
• Note that:

Let 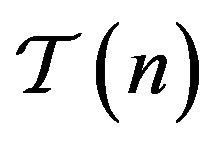 denote the class of functions
denote the class of functions 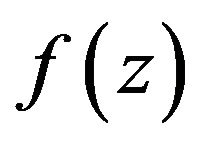 of the form
of the form
 (4)
(4)
which are analytic in the open unit disc.
Following the earlier investigations by [8] and [9], we define 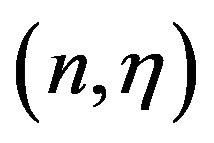 -neighborhood of a function
-neighborhood of a function 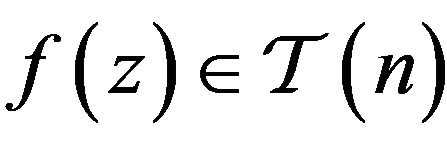 by
by

or,

where 
Let  denote the subclass of
denote the subclass of  consisting of functions which satisfy
consisting of functions which satisfy
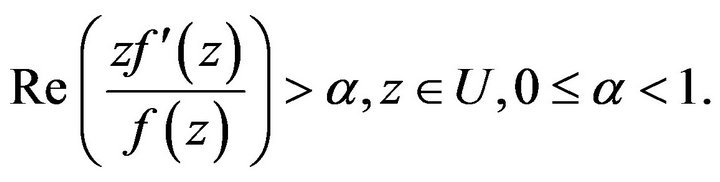
A function 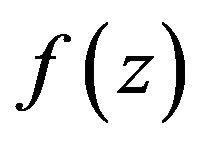 in
in 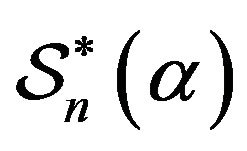 is said to be starlike of order
is said to be starlike of order 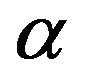 in
in .
.
A function  is said to be convex of order
is said to be convex of order  it it satisfies
it it satisfies

We denote by 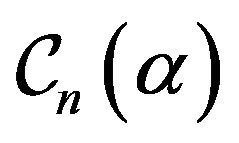 the subclass of
the subclass of  consisting of all such functions [10].
consisting of all such functions [10].
The unification of the classes  and
and  is provided by the class
is provided by the class 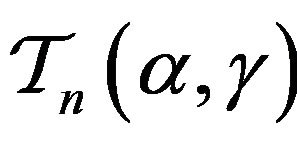 of functions
of functions 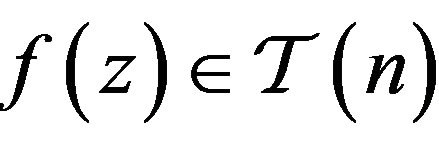 which also satisfy the following inequality
which also satisfy the following inequality

The class 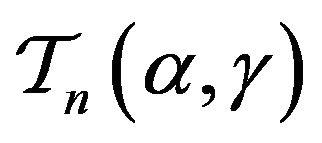 was investigated by Altintas [11].
was investigated by Altintas [11].
Now, by using  we will define a new class of starlike functions.
we will define a new class of starlike functions.
Definition 1.2 Let

A function 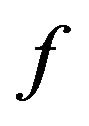 belonging to
belonging to  is said to be in the class
is said to be in the class  if and only if
if and only if
 (6)
(6)
Remark 1.3 The class 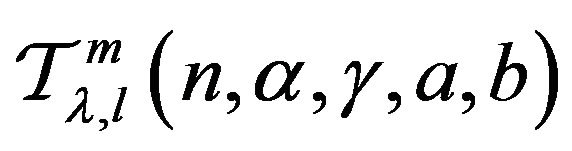 is a generalization of the following subclasses:
is a generalization of the following subclasses:
i) 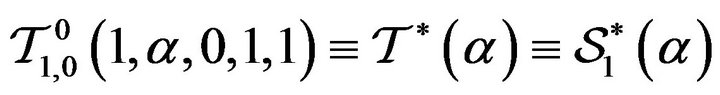 and
and
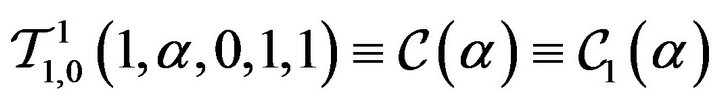 defined and studied by [12];
defined and studied by [12];
ii)  and
and 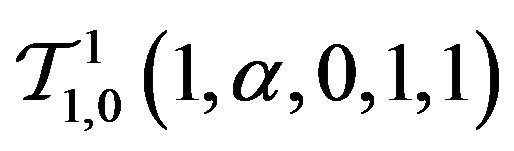 studied by [13] and [14];
studied by [13] and [14];
iii) 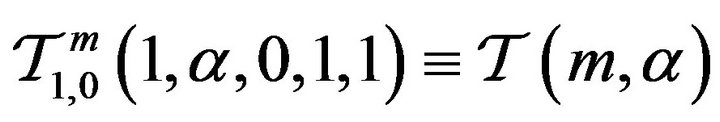 studied by [15];
studied by [15];
iv) 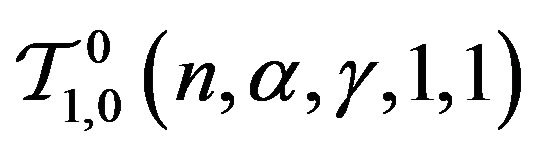 studied by [16].
studied by [16].
Now, we shall use the same method by [17] to establish certain coefficient estimates relating to the new introduced class.
2. Coefficient Estimates
Theorem 2.1 Let the function 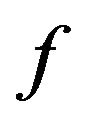 be defined by (1). Then
be defined by (1). Then 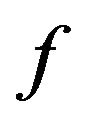 belongs to the class
belongs to the class  if and only if
if and only if
 (7)
(7)
where
 (8)
(8)
The result is sharp and the extremal functions are
 (9)
(9)
Proof: Assume that the inequality (7) holds and let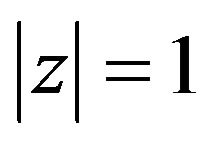 . Then we have
. Then we have

Consequently, by the maximum modulus theorem one obtains
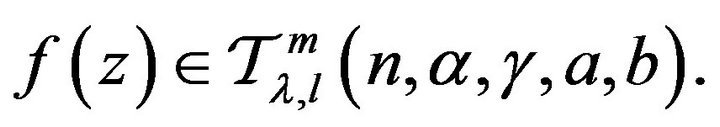
Conversely,suppose that
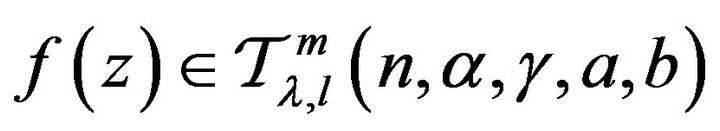 .
.
Then from (6) we find that

Choose values of 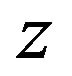 on the real axis such that
on the real axis such that
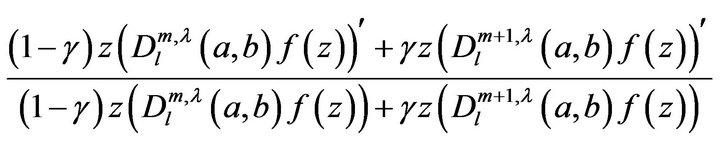
is real. Letting 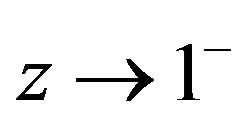 through real values, we obtain
through real values, we obtain
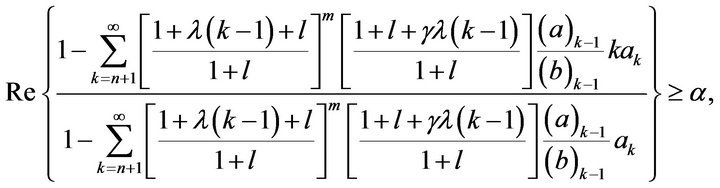
or, equivalently

which gives (7).
Remark 2.2 In the special case 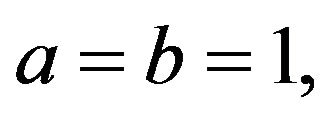 Theorem 2.1 yields a result given earlier by [17].
Theorem 2.1 yields a result given earlier by [17].
Remark 2.3 In the special case 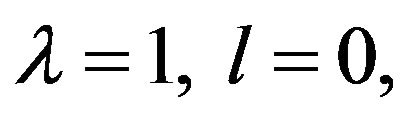
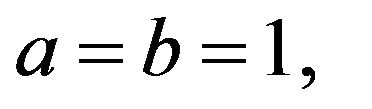 Theorem 2.2 yields a result given earlier by [6].
Theorem 2.2 yields a result given earlier by [6].
Theorem 2.4 Let the function 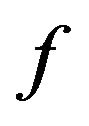 defined by (3) be in the class
defined by (3) be in the class . Then
. Then
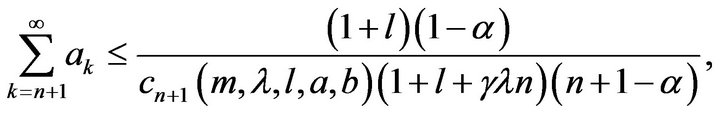 (10)
(10)
and
 (11)
(11)
The equality in (10) and (11) is attained for the function 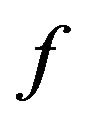 given by (9).
given by (9).
Proof: By using Theorem 2.2, we find from (6) that

which immediately yields the first assertion (10) of Theorem 2.3.
On the other hand, taking into account the inequality (6), we also have

that is

which, in view of the coefficient inequality (10), can be put in the form

and this completes the proof of (11).
3. Closure Theorem
Theorem 3.1 Let the function  be defined by
be defined by

for 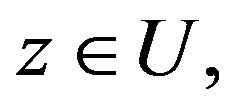 be in the class
be in the class  then the function
then the function 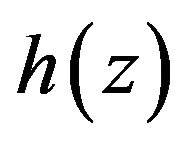 defined by
defined by

also belongs to the class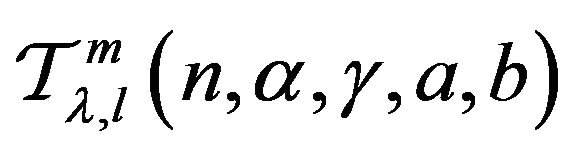 , where
, where

Proof: Since 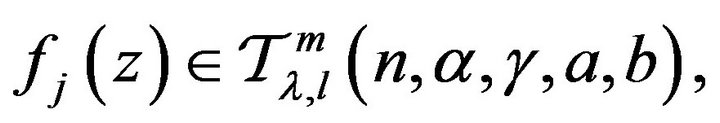 it follows from Theorem 2.1, that
it follows from Theorem 2.1, that
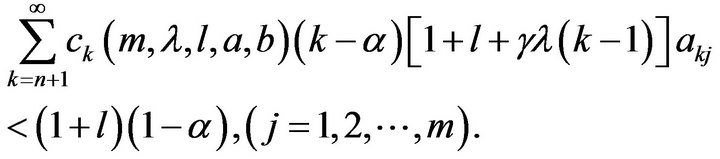
Therefore,
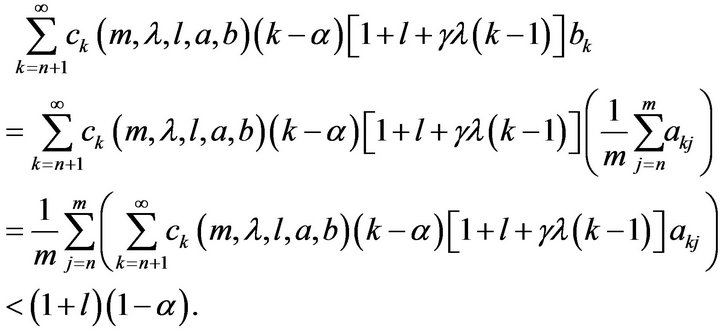
Hence by Theorem 2.1, 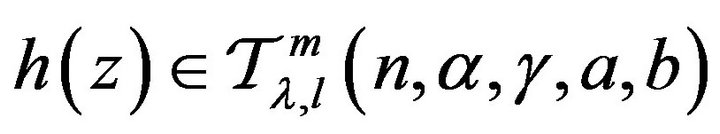 also.
also.
Morever, we shall use the same method by [17] to prove the distrotion Theorems.
4. Distortion Theorems
Theorem 4.1 Let the function  defined by (1) be in the class
defined by (1) be in the class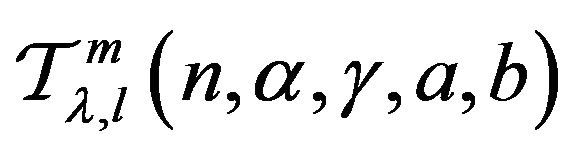 . Then we have
. Then we have
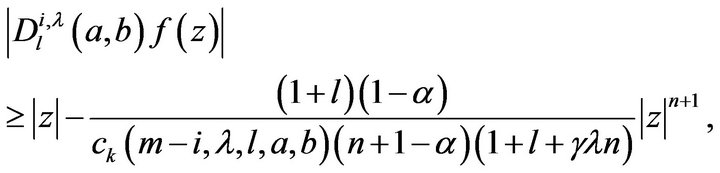 (12)
(12)
and
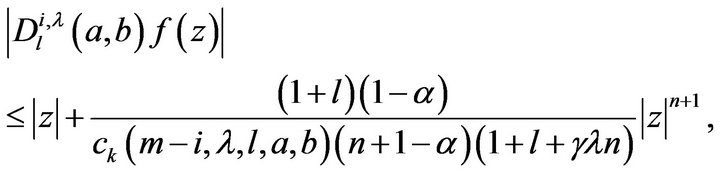 (13)
(13)
for , where
, where  and
and 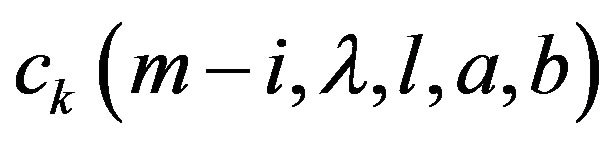 is given by (8).
is given by (8).
The equalities in (12) and (13) are attained for the function 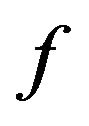 given by
given by
 (14)
(14)
Proof: Note that 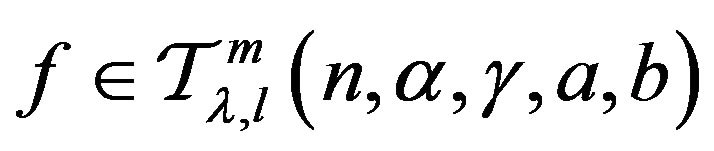 if and only if
if and only if
 , where
, where

By Theorem 2.2, we know that
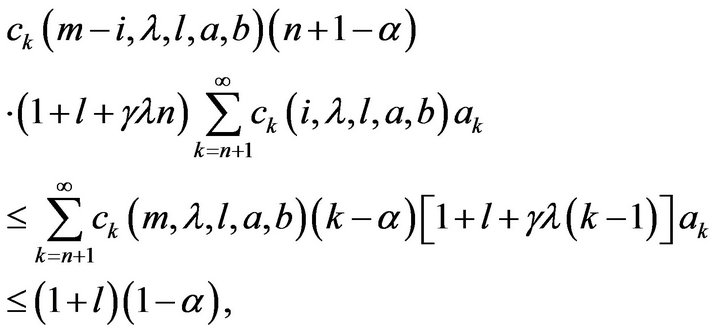
that is
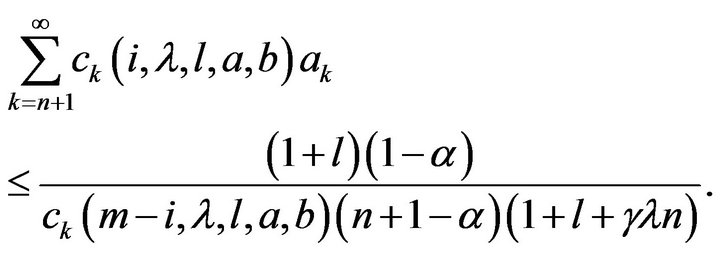
The assertions of (12) and (13) of Theorem 4.1 follow immediately. Finally, we note that the equalities (12) and (13) are attained for the function 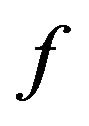 defined by
defined by
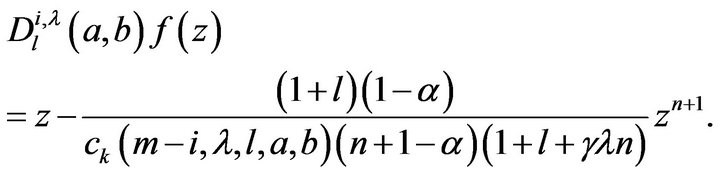
This completes the proof of Theorem 4.1.
Remark 4.2 In the special case  Theorem 4.1 yields a result given earlier by [17].
Theorem 4.1 yields a result given earlier by [17].
Corollary 4.3 Let the function 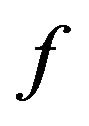 defined by (1) be in the class
defined by (1) be in the class . Then we have
. Then we have
 (15)
(15)
and
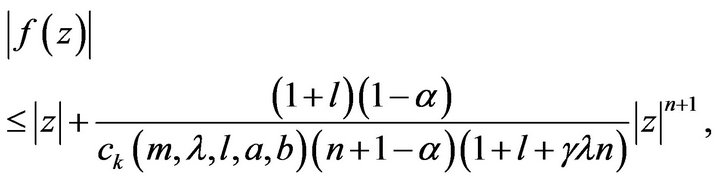 (16)
(16)
for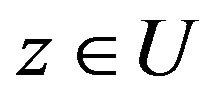 . The equalities in (15) and (16) are attained for the function
. The equalities in (15) and (16) are attained for the function 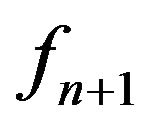 given in (14).
given in (14).
Corollary 4.4 Let the function  defined by (1) be in the class
defined by (1) be in the class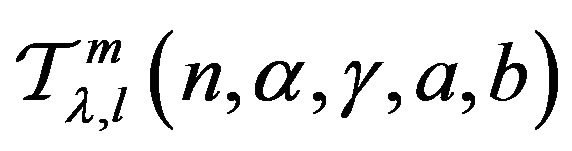 . Then we have
. Then we have
 (17)
(17)
and
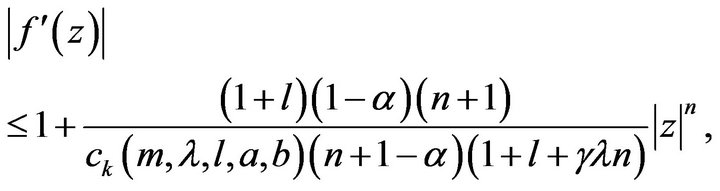 (18)
(18)
for . The equalities in (17) and (18) are attained for the function
. The equalities in (17) and (18) are attained for the function 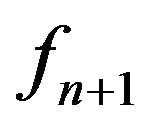 given in (14).
given in (14).
Corollary 4.5 Let the function 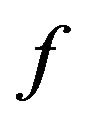 defined by (3) be in the class
defined by (3) be in the class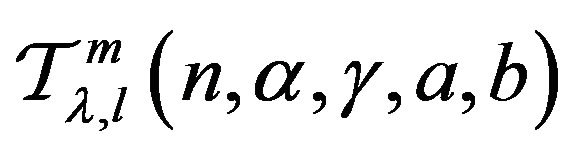 . Then the unit disc is mapped onto a domain that contains the disc
. Then the unit disc is mapped onto a domain that contains the disc
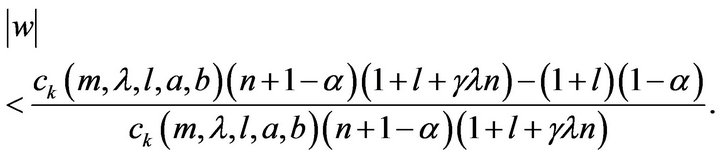
The result is sharp with the extremal function 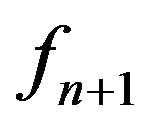 given in (14).
given in (14).
5. Integral Operators
Theorem 5.1 Let the function 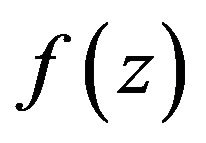 defined by (1) be in the class
defined by (1) be in the class 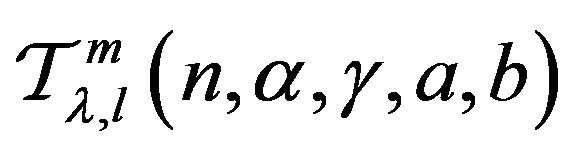 and let
and let  be a real number such that
be a real number such that  Then
Then 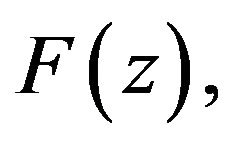 defined by
defined by
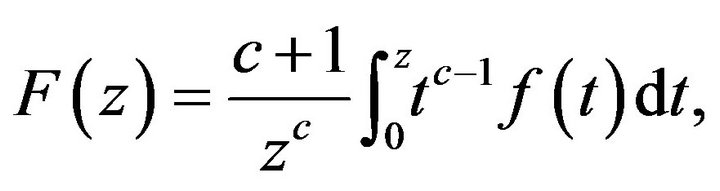
also belongs to the class 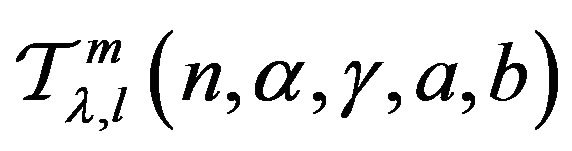
Proof: From the representation of 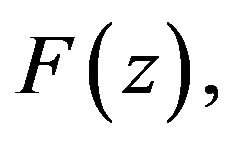 it is obtained that
it is obtained that

where

Therefore
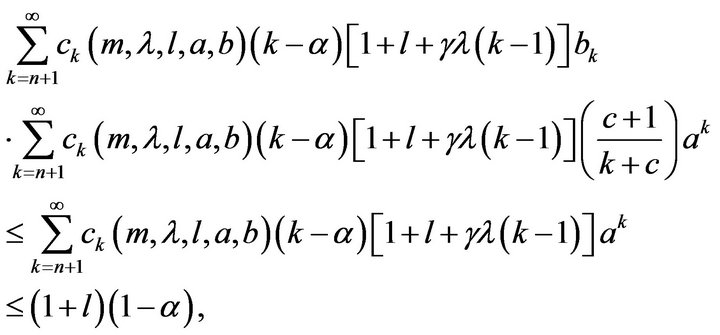
since 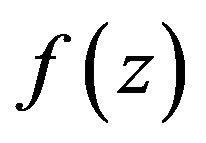 belongs to
belongs to 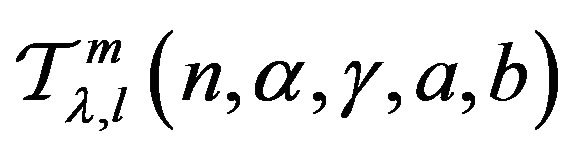 so by virtue of Theorem 2.1,
so by virtue of Theorem 2.1, 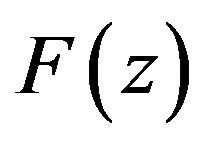 is also element of
is also element of

6. Acknowledgements
The work presented here was partially supported by LRGS/TD/2011/UKM/ICT/03/02.
NOTES