Homotopy Analysis Method for Large-Amplitude Free Vibrations of Strongly Nonlinear Generalized Duffing Oscillators ()
1. Introduction
Nonlinear Duffing equation is a simple mathematical model which describes the resonance and chaotic phenomenon. In science and engineering many nonlinear vibration problems can be transformed into the Duffing equation to research [1]. From a certain point, the real significance of the research on nonlinear Duffing system attracts a lot of scholars and several ingenious analytical methods have been developed for dealing with the nonlinear Duffing oscillator, such as the modified perturbation methods [2,3], improved harmonic balance methods [4], energy balance method [5,6], the frequency-amplitude formulation [7,8]. Meanwhile, the homotopy analysis method (HAM) [9] proposed by Liao has been proved to be one of the efficient analytical techniques in solving a variety of nonlinear Duffing problems. By the HAM, Hoseini et al. [10] study free vibrations of tapered beams and give an accurate analytical solution for the thirdorder Duffing equations; Qian et al. [11] obtain accurate analytical solutions for the fifth-order Duffing equations by considering vibrations of a restrained cantilever beam. For the seventh-order Duffing equations Qian et al. [12] get accurate analytical solutions by researching vibrations of an electrostatically actuated microbeam.
Thus, the prime objective of this paper is to explore the utility of the HAM for the generalized Duffing equation. All odd-type analytical results can be then involved in the generalized solution. In what follows, Section 2 presents natural frequency of the system obtained as a function of the initial amplitude and the general solution for any arbitrary odd power of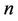 . In addition, the optimal HAM approach used to accelerate the convergence of solutions is also provided and discussed. In Section 3 two numerical examples are presented to examine the accuracy and validity of the proposed technique. In Section 4 the numerical results of the HAM are presented and compared with the numerical integration solutions. Finally, a conclusion summarizes the research findings in Section 5.
. In addition, the optimal HAM approach used to accelerate the convergence of solutions is also provided and discussed. In Section 3 two numerical examples are presented to examine the accuracy and validity of the proposed technique. In Section 4 the numerical results of the HAM are presented and compared with the numerical integration solutions. Finally, a conclusion summarizes the research findings in Section 5.
2. Solution Methodology
In this section, we apply the HAM to solve the following nonlinear Duffing oscillator:
 , (1)
, (1)
where  is displacement and
is displacement and  (n is the odd number) are arbitrary constants. Subject to the following initial conditions:
(n is the odd number) are arbitrary constants. Subject to the following initial conditions:
 , (2)
, (2)
where A is an arbitrary constant. Under the transformation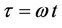 , Equations (1) and (2) can be rewritten as follows:
, Equations (1) and (2) can be rewritten as follows:
 , (3)
, (3)
 (4)
(4)
where a dot  denotes differentiation with respect to
denotes differentiation with respect to , and
, and  is the nonlinear frequency.
is the nonlinear frequency.
It is known that free oscillation of a conservative system without damping is a periodic motion and a harmonic function is the simplest type of periodic motion. So it can be expressed by the following base functions:
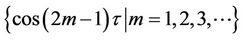 . (5)
. (5)
Taking into consideration the initial conditions in Equation (4), we choose the initial guess of 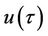 for the zeroth-order deformation equation as follows:
for the zeroth-order deformation equation as follows:
 . (6)
. (6)
Thus, the auxiliary linear operator of a conservative system can be selected as
 . (7)
. (7)
The auxiliary linear operator L is chosen in such a way that all solutions of the corresponding high-order formation equations exist and can be expressed by the general form of the base function. According to Equation (4), the nonlinear operator is written as:
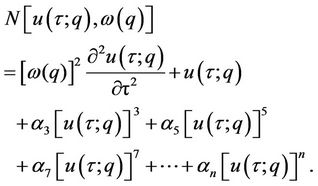 (8)
(8)
Then considering the homotopy function, we obtain the zeroth-order deformation equation as:
 , (9)
, (9)
where  and
and  are, respectively, embedding and convergence-control parameters. As q changes from 0 to 1,
are, respectively, embedding and convergence-control parameters. As q changes from 0 to 1, 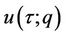 varies from the initial guess
varies from the initial guess  to the unknown solution
to the unknown solution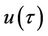 . Similarly,
. Similarly,  varies from the initial guess frequency
varies from the initial guess frequency 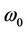 to the physical frequency
to the physical frequency .
.
Then we make use of the Taylor series expansion to get
 , (10)
, (10)
 , (11)
, (11)
in which
 , (12)
, (12)
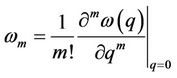 , (13)
, (13)
It is known that if  is properly chosen, the power series solutions in Equations (10) and (11) can be converged at
is properly chosen, the power series solutions in Equations (10) and (11) can be converged at . So Equations (10) and (11) then become
. So Equations (10) and (11) then become
 , (14)
, (14)
 . (15)
. (15)
For the sake of simplicity, we define the following vectors:
 (16)
(16)
By differentiating the zeroth-order deformation equation (9) m times with respect to q, then the resulting equation is divided m! and setting , it can be found the mth-order deformation equation
, it can be found the mth-order deformation equation
 , (17)
, (17)
with the initial conditions:
 , (18)
, (18)
in which
 , (19)
, (19)
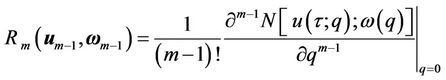 . (20)
. (20)
Because odd nonlinearity of considered conservative system,  can also be written as:
can also be written as:
 , (21)
, (21)
where 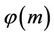 is an integer that depends on
is an integer that depends on .
.
Following the rule of solution expression and the linear operator , the terms of
, the terms of 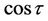 should not exist in
should not exist in  of Equation (17), otherwise the so-called secular terms such as
of Equation (17), otherwise the so-called secular terms such as 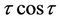 will appear in the final solutions. Therefore, their coefficients are set to zero as follows:
will appear in the final solutions. Therefore, their coefficients are set to zero as follows:
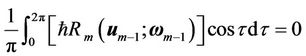 , (22)
, (22)
The solutions of  in Equations (17) and (22) can be determined successively. For the given values of
in Equations (17) and (22) can be determined successively. For the given values of  and
and , we have the periodic solutions by the abovementioned analytical approach,
, we have the periodic solutions by the abovementioned analytical approach,
 (23)
(23)
where  and
and  can be determined by using the initial condition given in Equation (18).
can be determined by using the initial condition given in Equation (18).
Hence, the mth-order approximations are
 (24)
(24)
in which
 . (25)
. (25)
We know there are many optimal HAM approaches, which can be able to achieve faster convergent homotopy-series solutions [13,14]. In theory, we can define the exact residual error of the mth-order of approximation as
 . (26)
. (26)
where  is the exact nonlinear frequency of Equation (1) derived by using the numerical integration technique. It can be found ∆m embraces the unknown convergencecontrol parameter
is the exact nonlinear frequency of Equation (1) derived by using the numerical integration technique. It can be found ∆m embraces the unknown convergencecontrol parameter . As ∆m decreases more rapidly to zero, the speed of the convergence for the corresponding homotopy-series solution is faster [14]. The corresponding value of the convergence-control parameter
. As ∆m decreases more rapidly to zero, the speed of the convergence for the corresponding homotopy-series solution is faster [14]. The corresponding value of the convergence-control parameter  at the given order of approximation
at the given order of approximation  can be optimized and selected by minimizing the residual error ∆m.
can be optimized and selected by minimizing the residual error ∆m.
3. Numerical Results
It can be obviously found the nonlinear Duffing oscillator for  has a simple form. So in this section, we research the nonlinear Duffing oscillator for
has a simple form. So in this section, we research the nonlinear Duffing oscillator for  and
and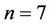 .
.
Firstly the nonlinear Duffing oscillator for  has the following form:
has the following form:
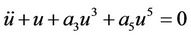 . (27)
. (27)
The problem is solved and the general solution can be obtained based on the HAM in Section 2.
For , one obtains
, one obtains  from Equation (22) as follows
from Equation (22) as follows
 . (28)
. (28)
Making use of Equation (23) leads to
 (29)
(29)
where
 , (30)
, (30)
 . (31)
. (31)
For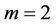 , we substitute the solutions of
, we substitute the solutions of ,
,  and
and  into Equation (22) to yield
into Equation (22) to yield
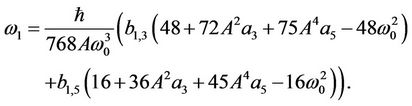 (32)
(32)
From Equation (21),  are derived in the following:
are derived in the following:
 (33)
(33)
where the coefficients 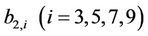 can be readily derived using Equation (21). In addition,
can be readily derived using Equation (21). In addition,  is given by
is given by
 (34)
(34)
For , we can yield
, we can yield
 (35)
(35)
 (36)
(36)
 (37)
(37)
where all coefficients 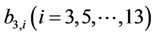 can be computed from Equation (21).
can be computed from Equation (21).
According to Equations (24) and (25), the corresponding third-order analytical approximation for Equation (27) is
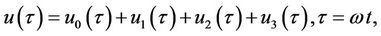 (38)
(38)
where
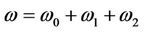 . (39)
. (39)
The higher-order approximations for  and
and  can be derived in a similar manner.
can be derived in a similar manner.
Secondly we consider the nonlinear Duffing oscillator for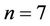 :
:
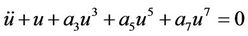 , (40)
, (40)
We can get some approximations for  and
and  according to Section 2 in a similar manner.
according to Section 2 in a similar manner.
For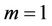 , one obtains
, one obtains
 , (41)
, (41)
 (42)
(42)
where
 , (43)
, (43)
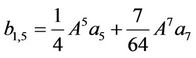 , (44)
, (44)
 . (45)
. (45)
For , we can yield
, we can yield
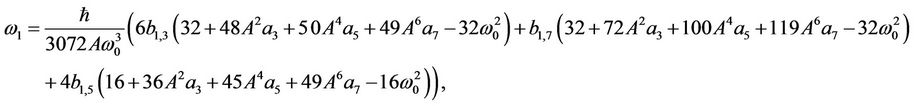 (46)
(46)
 (47)
(47)
 (48)
(48)
For , one arrives at
, one arrives at
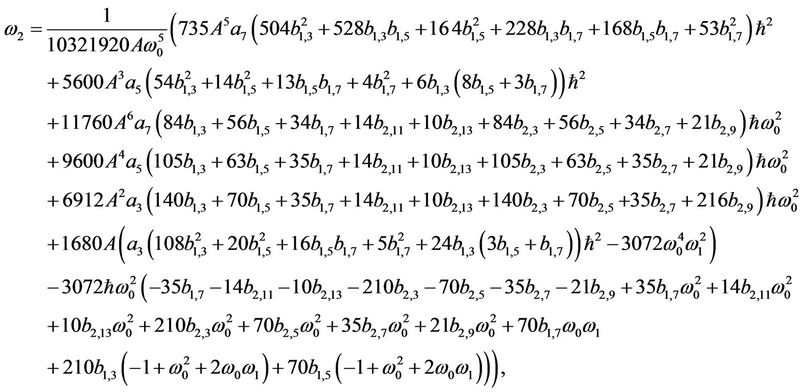 (49)
(49)
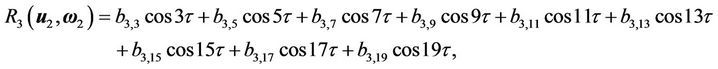 (50)
(50)
 (51)
(51)
where all coefficients  and
and  can be computed from Equation (21).
can be computed from Equation (21).
Similarly, the corresponding third-order analytical approximation for Equation (40) is
 (52)
(52)
where
 . (53)
. (53)
The higher-order approximations for  and
and  can be derived in a similar manner.
can be derived in a similar manner.
4. Numerical Discussion
In order to demonstrate the effectiveness of the presenting method, the asymptotic analytical solutions obtained by the HAM are directly compared to the published analytical and numerical integration solutions. Tables 1-4 present the results of He’s frequency-amplitude formulation  [15], He’s energy balance method
[15], He’s energy balance method  [15], presents approach
[15], presents approach 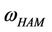 and exact solution
and exact solution  for various parameters
for various parameters 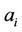 and amplitudes
and amplitudes .
.
In comparison with the exact solutions  in Tables 1 and 2, it can be distinctly observed the second-order HAM solutions
in Tables 1 and 2, it can be distinctly observed the second-order HAM solutions  for
for 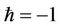 are better than the first-order solutions of
are better than the first-order solutions of  and
and . Moreover it can be checked that the HAM has a better performance for large amplitudes of motion.
. Moreover it can be checked that the HAM has a better performance for large amplitudes of motion.
In order to illustrate the effect of the convergencecontrol parameter , we can make use of Equation (26)
, we can make use of Equation (26)
to optimize  and draw the
and draw the  curve to obtain the optimal convergence-control parameter
curve to obtain the optimal convergence-control parameter .
.
By Figure 1, we get the optimal convergence-control parameters  in Table 3 for Modes 1-6. In Table 3 and Table 4, the results of
in Table 3 for Modes 1-6. In Table 3 and Table 4, the results of 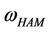 for the previous cases are refined in using the optimal parameters
for the previous cases are refined in using the optimal parameters . Because the parameter
. Because the parameter  is almost equal to the optimal value
is almost equal to the optimal value  in the Tables, thus, it is not very evident to show the power about the auxiliary parameter
in the Tables, thus, it is not very evident to show the power about the auxiliary parameter . But the value of
. But the value of  is one of the dominant factors in the HAM to extend its validity and flexibility. This also shows the good performance of investigating the nonlinear Duffing equations in this paper using the HAM.
is one of the dominant factors in the HAM to extend its validity and flexibility. This also shows the good performance of investigating the nonlinear Duffing equations in this paper using the HAM.
Figures 2 and 3 show the phase portrait diagrams and time history responses of Tables 1 and 2 where 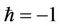 is chosen. We can clearly find that the third-order HAM solutions are in good agreement with the numerical integration solutions even if the amplitude is larger.
is chosen. We can clearly find that the third-order HAM solutions are in good agreement with the numerical integration solutions even if the amplitude is larger.
5. Conclusion
In this study, the HAM has intensively studied the generalized Duffing equation. The general frequencies and periodic solutions are presented for any arbitrary oddtype of nonlinearity. The purposes of this paper are not only to formulate the asymptotic approximate solutions for the nonlinear Duffing oscillators, but also to furnish a guidance to establish the higher-order asymptotic analytical approximations if necessary. Moreover, it is found that the accuracy of the HAM is affected by the selection
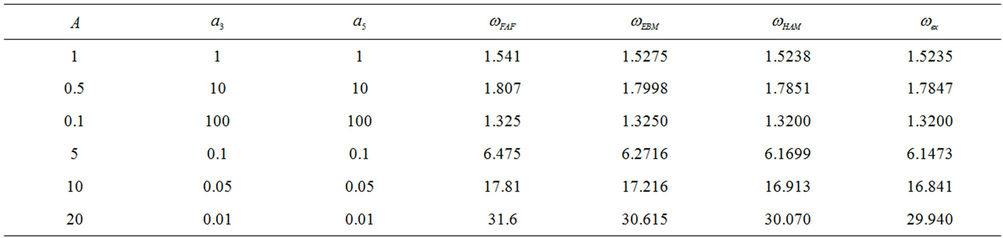
Table 1. Comparison of the exact and approximate frequencies corresponding to various parameters in Equation (27) for .
.

Table 2. Comparison of the exact and approximate frequencies corresponding to various parameters in Equation (40) for .
.

Table 3. Comparison of the approximate frequencies using the optimal convergence-control parameter  with the exact solution for n = 5.
with the exact solution for n = 5.

Table 4. Comparison of the approximate frequencies using the optimal convergence-control parameter  with the exact solution for n = 7.
with the exact solution for n = 7.
of appropriate convergence-control parameter . To further improve the accuracy of solutions, the parameter
. To further improve the accuracy of solutions, the parameter 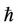 can be optimized and determined by the minimization of the residual error
can be optimized and determined by the minimization of the residual error  for any given order approximation
for any given order approximation . Besides, illustrative examples are applied as crucial evidence to support that the HAM is effective for the quantitative analysis of nonlinear problems. Finally, this paper suggests to readers to apply the method for solving nonlinear large-amplitude oscillations because of its accuracy, reliability and simplicity.
. Besides, illustrative examples are applied as crucial evidence to support that the HAM is effective for the quantitative analysis of nonlinear problems. Finally, this paper suggests to readers to apply the method for solving nonlinear large-amplitude oscillations because of its accuracy, reliability and simplicity.
6. Acknowledgements
The authors gratefully acknowledge the support of the National Natural Science Foundation of China (NNSFC) through grant No.11202189 and the National Natural Science Foundation of Zhejiang through grant No. LY12A02002.
NOTES