A Quick Method for Judging the Feasibility of Security-Constrained Unit Commitment Problems within Lagrangian Relaxation Framework ()
1. Introduction
Security-constrained Unit commitment (SCUC) is one of the most important daily functions for independent system operators (ISOs) to clear the electric power market and for generation companies (GENCOs) to analyze generation costs and determine bidding strategies [1-3]. The objective of SCUC is to minimize the total bid cost in current electric power market or generating cost in traditional power systems while satisfying the system constraints including system demand balance, system spinning reserve and related transmission security constraints, and individual unit operating limits such as minimum/maximum generation level, minimum up/down times, ramping rate constraints.
Since the SCUC is an NP-hard mixed integer-programming problem, it is extremely difficult to obtain the exact optimal solution within acceptable time [4]. Lagrangian Relaxation (LR) is one of the most successful methods for obtaining suboptimal solutions [5], where Lagrange multipliers relax the system-wide constraints such as system demand balance, system spinning reserve and DC transmission constraints. Some methods, usually heuristics are needed to modify the dual solution into a feasible one. In fact, the Lagrangian based SCUC methods are all similar but the ways to obtain feasible solutions may vary significantly.
It is clear that the core to develop an effective method for solving SCUC problems within the Lagrangian relaxation framework is how to obtain feasible solutions. First of all, a necessary or sufficient condition used for checking promptly on the feasibility of SCUC states is crucial. Our previous work [6] proposed such conditions. However, a necessary and sufficient condition for determining the feasibility of SCUC states at each scheduling time is not given. Furthermore, ramp rate constraints are not taken into consideration in those results.
A necessary and sufficient condition for determining the feasibility of SCUC states at each scheduling time is proposed and proven rigorously in this paper based on the Benders Decomposition Feasibility Theorem [7,8]. The condition is very crucial for constructing a feasible solution of a SCUC problem. Numerical test example shows that the presented condition is very efficient.
2. Problem Formulation of SCUC Problems
For the convenience of presentation, some notations are defined as follows.
 : commitment horizon in hours;
: commitment horizon in hours;
 : number of units with the index
: number of units with the index 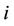 denoting the
denoting the  unit;
unit;
 : power generation by unit i at time t;
: power generation by unit i at time t;
 : binary variable: 1 if the
: binary variable: 1 if the  unit is turned on or kept on during the time period
unit is turned on or kept on during the time period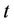 , else 0;
, else 0;
 : the number of time periods that Unit
: the number of time periods that Unit  has been up (
has been up ( )or down (
)or down (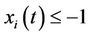 );
);
 : the minimum number of time periods for which the unit
: the minimum number of time periods for which the unit  must be up;
must be up;
 : the minimum number of time periods for which the unit
: the minimum number of time periods for which the unit 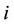 must be down;
must be down;
 : fuel cost of producing power
: fuel cost of producing power  for thermal unit
for thermal unit ;
;
 : startup/shutdown cost for unit
: startup/shutdown cost for unit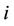 ;
;
 : total demand of the whole power system during time period
: total demand of the whole power system during time period ;
;
 : the spinning reserve requirement during time period
: the spinning reserve requirement during time period ;
;
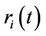 :
: 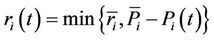 is the spinning reserve requirement during time period
is the spinning reserve requirement during time period ,
,  is the maximum spinning reserve requirement;
is the maximum spinning reserve requirement;
 : the maximum generation of unit
: the maximum generation of unit  at scheduling time
at scheduling time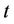 , if unit
, if unit  has no raping limit,
has no raping limit, ;
;
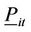 : the minimum generation of unit
: the minimum generation of unit  at scheduling time
at scheduling time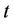 , if unit
, if unit  has no raping limit,
has no raping limit,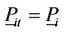 ;
;
 : the maximum ramp rate;
: the maximum ramp rate;
The objective of the unit commitment problem is to minimize the total operating cost as the following mixed integer-programming problem:
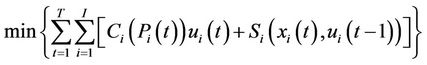 , (1)
, (1)
subject to
2.1. System Level Constraints
1) System demand constraint
 , (2)
, (2)
where  is the demand at bus
is the demand at bus ;
;
2) Spinning reserve constraint:
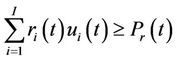 , (3)
, (3)
where  is the maximum spinning reserve requirement.
is the maximum spinning reserve requirement.
3) Transmission security constraints:
 (4)
(4)
2.2. Individual Unit Constraints
4) The minimum up/down time constraint:
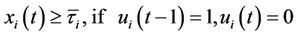 , (5)
, (5)
 , (6)
, (6)
5) The relation between the unit state and unit up/ down decision
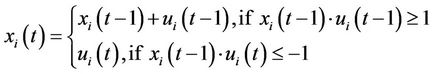 (7)
(7)
6) Generation constraint
 (8)
(8)
7) Ramp rate constraints: if
 then
then
 , (9)
, (9)
8) Minimal power generation constraint at the first/last up hour:
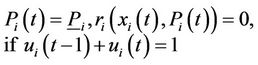 (10)
(10)
3. The New Necessary and Sufficient Condition for Checking the Feasibility of SCUC States
A mixed-integer programming problem can be represented as
 , (11)
, (11)
where 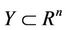 is assumed to be a nonempty convex set and
is assumed to be a nonempty convex set and 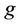 is concave on Y for each fixed
is concave on Y for each fixed ,
, 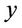 and
and  are continuous and discrete variables, respectively.
are continuous and discrete variables, respectively.
Definition: A vector  is called to be quasifeasible if there exists a vector
is called to be quasifeasible if there exists a vector  such that
such that .
.
Benders Decomposition Feasibility Theorem [7,8]: For problem (11),  and
and 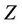 are nonempty and
are nonempty and 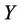 is convex, the vector function
is convex, the vector function  is concave vector function for each
is concave vector function for each . Furthermore, the set
. Furthermore, the set
 (12)
(12)
is closed for each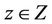 . Then
. Then  is quasifeasible if and only if the following inequalities are satisfied for
is quasifeasible if and only if the following inequalities are satisfied for 
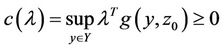 , (13)
, (13)
where
 , (14)
, (14)
 , (15)
, (15)
Note 1: The result still holds for all .
.
Note 2: A SCUC problem can be written as the form of Equation (11), where
 , (16)
, (16)
 , (17)
, (17)
and  is the number of generating units at scheduling time
is the number of generating units at scheduling time ,
,  are the indices of generating units,
are the indices of generating units,  and
and  are the minimal and maximal power generation of unit
are the minimal and maximal power generation of unit  level, respectively.
level, respectively.  is a
is a  vector function, of which the first and second dimensions corresponds to the system demand constraint (since such constraint can be represented as two inequalities), the third relates to the spinning reserve constraint, and the rest dimensions correspond to
vector function, of which the first and second dimensions corresponds to the system demand constraint (since such constraint can be represented as two inequalities), the third relates to the spinning reserve constraint, and the rest dimensions correspond to  transmission security constraints.
transmission security constraints.  is the total cost including the fuel cost of all generating units at time
is the total cost including the fuel cost of all generating units at time  and their startup cost.
and their startup cost.
Since for SCUC state vector  at each scheduling time
at each scheduling time 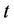 the power generation of units not being started up need not be optimized, the set
the power generation of units not being started up need not be optimized, the set  is determined by
is determined by  and is a convex cube of
and is a convex cube of . For the given SCUC state vector
. For the given SCUC state vector ,
,  is the continuous concave vector function over the closed convex set
is the continuous concave vector function over the closed convex set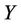 , and hence
, and hence  is closed. Therefore, at each scheduling time
is closed. Therefore, at each scheduling time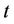 , the SCUC problem is a mixed-integer programming of the form (11), which satisfies the conditions of the above Benders Decomposition Feasibility Theorem.
, the SCUC problem is a mixed-integer programming of the form (11), which satisfies the conditions of the above Benders Decomposition Feasibility Theorem.
To obtain the desired result, the units are classified into three categories at time t: 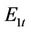 is the set of units which is on the normal generating state;
is the set of units which is on the normal generating state; 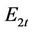 is the set of units at the first/last generating hour;
is the set of units at the first/last generating hour;  is the set of units with ramp rate constraints. The set
is the set of units with ramp rate constraints. The set  is further classified into four types, named as
is further classified into four types, named as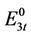 ,
,  ,
, 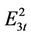 and
and 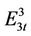 respectively, as follows:
respectively, as follows:

Using the Benders Decomposition Feasibility Theorem, we obtain the desired necessary and sufficient condition for SCUC states to be feasible.
Theorem: SCUC states at scheduling time  is quasifeasible if and only if the optimal value of the following nonlinear program is nonnegative:
is quasifeasible if and only if the optimal value of the following nonlinear program is nonnegative:
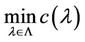 , (18)
, (18)
where

and

Proof: The left hand side of the Benders Decomposition Feasibility Theorem is
 (19)
(19)
where

The solution of problem (19) depends on the following subproblems since the problem (19) is decomposable with respect to units:
i) Subproblem 1: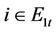 , we have
, we have

ii) Subproblem 2: , we have
, we have

iii) Subproblem 3: , we have
, we have

iv) Subproblem 4: , we have
, we have

v) Subproblem 5: , we have
, we have

By Benders Decomposition Feasibility Theorem, we have the desired result. Q.E.D.
Note 3: The all subproblems above are linear programming problems with simple constraints. Thus, by comparing the values of all extreme points, the optimal solutions and corresponding optimal values can be obtained easily.
Note 4: It should be noted that the theorem still hold for .
.
4. The Numerical Solution of the Problem
Consider the SCUC problem at scheduling time 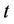 with 0 being the objective
with 0 being the objective
 (20)
(20)
where ,
,  and
and  are defined in Equations (16)-(17). The dual problem of the problem (20) is
are defined in Equations (16)-(17). The dual problem of the problem (20) is
 , (21)
, (21)
By the theorem and the note 4,  is quasi-feasible if and only if and only if the optimal value of
is quasi-feasible if and only if and only if the optimal value of 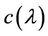 is nonnegative over the positive orthant
is nonnegative over the positive orthant . While the problem (21) can be solved by using subgradient method [9], and the value
. While the problem (21) can be solved by using subgradient method [9], and the value  can be obtained by Equation (19) for the given Lagrange multiplier vector
can be obtained by Equation (19) for the given Lagrange multiplier vector , the Lagrange multiplier can then be updated by subgradient method. Since the best multiplier vector in the dual iteration of the SCUC problem is taken as the initial multiplier
, the Lagrange multiplier can then be updated by subgradient method. Since the best multiplier vector in the dual iteration of the SCUC problem is taken as the initial multiplier , the rate of convergence of
, the rate of convergence of  is quite promptly.
is quite promptly.
5. Numerical Testing Result
The standard IEEE example [5] tests the effectiveness and efficiency of the proposed method (Figure 1), which has 16 units, 43 transmission lines, 31 buses (of which 11 is load bus). The fuel cost function of unit  is
is

The data of units, the system reserve requirement , the system demand
, the system demand at each scheduling time
at each scheduling time , the maximal value of DC power flow
, the maximal value of DC power flow  on each transmission line
on each transmission line  and the amount of electric power on each load bus are given in Tables 1-5, respectively. Units 1 and 4 have minimal power generation constraint at the first/last up hour.
and the amount of electric power on each load bus are given in Tables 1-5, respectively. Units 1 and 4 have minimal power generation constraint at the first/last up hour.
The CPU-time is within 2.3 second for checking SCUC states for 24 scheduling period on a DELL Computer with 2G RAM using MATLAB 7.01. Table 6 gives a feasible SCUC obtained within Lagrangian framework. Figure 2 presented the tendency of  with
with  at
at . Testing example shows that the numerical method for determining the feasibility of a SCUC is effective and efficient.
. Testing example shows that the numerical method for determining the feasibility of a SCUC is effective and efficient.
6. Conclusions
The key of solving SCUC problems is to determine whether a SCUC is quasi-feasible or not. The existence of ramp rate constraints and transmission security constraints increases the difficulty of obtaining an analytical condition. However, a numerical necessary and sufficient condition for checking on the feasibility of SCUC states at each scheduling time is proposed and proved rigorously based on Benders Decomposition Feasibility

Table 1. Generation level and its coefficient of fuel cost function of each unit.

Figure 1. The one-line diagram for the 31-bus test system.

Table 2. Length of up/down time, initial states and coefficient of startup cost function of each unit.

Table 3. System load and system reserve requirement for 24 scheduling hours.


Table 4. Limits of DC power flow  on each transmission line.
on each transmission line.

Table 5. Percent of system load drawn by load bus.

Table 6. A Feasible SCUC obtained within Lagrangian relaxation framework.

Figure 2. The tendency of 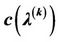 with
with  at t = 8 in the first dual iteration of the SCUC problem. The SCUC at t = 8 is feasible.
at t = 8 in the first dual iteration of the SCUC problem. The SCUC at t = 8 is feasible.
Theorem. The condition is very crucial for constructing a feasible solution of a SCUC problem. Numerical testing example shows that the proposed condition is very effective and efficient.
NOTES