1. Introduction
The BFSS matrix theory is conjectured to describe infinite momentum frame (IMF) limit of M-theory in [2] and many evidences were found. However, because of the limit, SO(1,10) symmetry is not manifest in these models; it includes only time and nine matrices corresponding to nine spatial coordinates. As a result, it is very difficult to derive full dynamics of M-theory. For example, we do not know the manner to describe longitudinal momentum transfer of D0-branes. Therefore, we need a covariant matrix model for M-theory that possesses manifest SO (1,10) symmetry.
Recently, structures of 3-algebras [3-5] were found in the effective actions of the multiple M2-branes [6-14]1 and 3-algebras have been intensively studied [15-31]. One can expect that structures of 3-algebras play more fundamental roles in M-theory2 than the accidental structures in the effective descriptions.
The BFSS matrix theory and the IIB matrix model [35] can be obtained by the matrix regularization of the Poisson brackets of the light-cone membrane theory [36] and of Green-Schwarz string theory in Schild gauge [35], respectively. Because the regularization replaces a twodimensional integral over a world volume by a trace over matrices, the BFSS matrix theory and the IIB matrix model are one-dimensional and zero-dimensional field theories, respectively. On the other hand, the bosonic part of the membrane action has a structures of a 3-algebra. That is, it can be written in the 3-algebra manifest form as

where  denotes Nambu-Poisson bracket [15,16]. Therefore, a bosonic covariant 3-algebra model for Mtheory was proposed in [1].
denotes Nambu-Poisson bracket [15,16]. Therefore, a bosonic covariant 3-algebra model for Mtheory was proposed in [1].
In this paper, we examine a natural supersymmetric extension of the bosonic covariant model in [1]3,
 (1)
(1)
The bosons  and the Majorana fermions
and the Majorana fermions  are spanned by the elements of the Lorentzian Lie 3-algebra associated with the U(N) Lie algebra. This action defines a zero-dimensional field theory and possesses manifest SO(1,10) symmetry. By expanding fields around appropriate vacua, we derive the BFSS matrix theory and the IIB matrix model in a large N limit.
are spanned by the elements of the Lorentzian Lie 3-algebra associated with the U(N) Lie algebra. This action defines a zero-dimensional field theory and possesses manifest SO(1,10) symmetry. By expanding fields around appropriate vacua, we derive the BFSS matrix theory and the IIB matrix model in a large N limit.
2. A Supersymmetric Extension
We examine a following model,
 (1)
(1)
where  with
with  are vectors and
are vectors and  are Majorana spinors of SO(1,10). This action defines a zero-dimensional field theory and possesses manifest SO (1,10) symmetry. There is no coupling constant.
are Majorana spinors of SO(1,10). This action defines a zero-dimensional field theory and possesses manifest SO (1,10) symmetry. There is no coupling constant.
 and
and  are spanned by the elements of the Lorentzian Lie 3-algebra associated with the U(N) Lie algebra,
are spanned by the elements of the Lorentzian Lie 3-algebra associated with the U(N) Lie algebra,
 (2)
(2)
where  The algebra is defined by
The algebra is defined by
 (3)
(3)
where 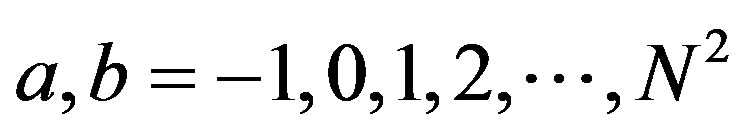 and
and  is totally anti-symmetrized.
is totally anti-symmetrized.  is a Lie bracket of the U(N) Lie algebra. The metric of the elements is defined by
is a Lie bracket of the U(N) Lie algebra. The metric of the elements is defined by
 (4)
(4)
By using these relations, the action is rewritten as
 (5)
(5)
where  and
and . There is no ghost in the theory, because
. There is no ghost in the theory, because 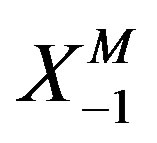 or
or  does not appear in the action4.
does not appear in the action4.
Let us summarize symmetry of the action. First, gauge symmetry is the  -dimensional translation and U(N) symmetry associated with the Lorentzian Lie 3-algebra [10].
-dimensional translation and U(N) symmetry associated with the Lorentzian Lie 3-algebra [10].
Second, there are two kinds of shift symmetry. First one is the eleven-dimensional translation symmetry generated by
 (6)
(6)
Where ,
,  and the other fields are not transformed. Second one is a part of supersymmetry, so called the kinematical supersymmetry, generated by
and the other fields are not transformed. Second one is a part of supersymmetry, so called the kinematical supersymmetry, generated by
 (7)
(7)
where ,
,  and the other fields are not transformed.
and the other fields are not transformed.
Third, the action is invariant under another part of supersymmetry transformation, so called the dynamical supersymmetry transformation,
 (8)
(8)
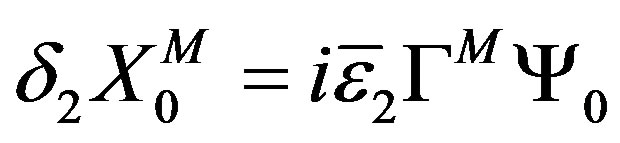 (9)
(9)
 (10)
(10)
 (11)
(11)
where  and
and  is the variation of the action (5) under (8), (9) and (10).
is the variation of the action (5) under (8), (9) and (10).
We should note that the above super transformation is slightly different with a 3-algebra manifest super transformation, which is a straightforward analogue to that of the BLG theory for multiple M2-branes;
 (12)
(12)
If we decompose this transformation, (8), (9) and (10) are the same, but (11) is different. In the analogue case,  There is no such symmetry5 because
There is no such symmetry5 because 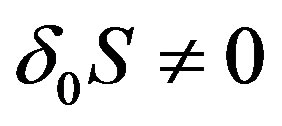 .
.
In the Lorentzian case, the action does possess supersymmetry because 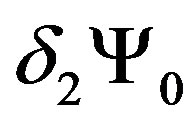 cancels
cancels . However,
. However,  is inconsistent with the 3-algebra symmetry. As a result, the supersymmetry algebra does not close, although it closes in a
is inconsistent with the 3-algebra symmetry. As a result, the supersymmetry algebra does not close, although it closes in a 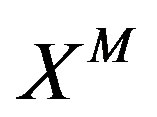 sector as one can see below.
sector as one can see below.
The commutators among the supersymmetry transformations act on 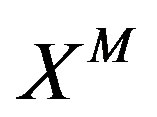 as
as



where .
.
If we change a basis of the supersymmetry transformations as
 (13)
(13)
up to the gauge transformation, we obtain
 (14)
(14)
where  is a translation.
is a translation.
These 64 supersymmetry transformations are summarised as  and (14) implies the
and (14) implies the  supersymmetry algebra in eleven dimensions in the
supersymmetry algebra in eleven dimensions in the  sector,
sector,
 (15)
(15)
Because the low energy effective description of Mtheory is given by the  eleven-dimensional supergravity, the
eleven-dimensional supergravity, the  supersymmetry in this sector is necessarily broken into the
supersymmetry in this sector is necessarily broken into the 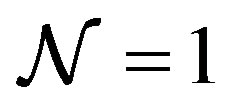 supersymmetry, spontaneously. In the next section, we will show that the model reduces to the BFSS matrix theory and the IIB matrix model in a large N limit if appropriate vacua are chosen.
supersymmetry, spontaneously. In the next section, we will show that the model reduces to the BFSS matrix theory and the IIB matrix model in a large N limit if appropriate vacua are chosen.
Because the commutators among the supersymmetry transformations of  result in the eleven-dimensional translation (6), eigen values of
result in the eleven-dimensional translation (6), eigen values of  should be interpreted as eleven-dimensional space-time6. In the next section, when we derive the BFSS matrix theory and the IIB matrix model,
should be interpreted as eleven-dimensional space-time6. In the next section, when we derive the BFSS matrix theory and the IIB matrix model,  and
and 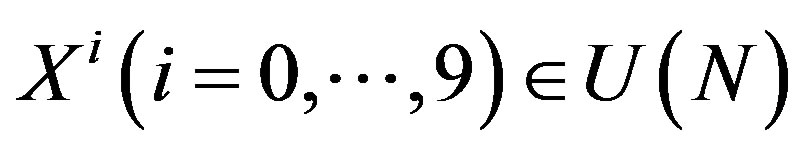 are identified with matrices in the BFSS matrix theory and the IIB matrix model respectively. Therefore, our interpretation is consistent with the space-time interpretation in these models.
are identified with matrices in the BFSS matrix theory and the IIB matrix model respectively. Therefore, our interpretation is consistent with the space-time interpretation in these models.
3. BFSS Matrix Theory and IIB Matrix Model from Covariant 3-Algebra Model for M-Theory
The covariant 3-algebra model for M-theory possesses a large moduli that includes simultaneously diagonalizable configurations. By treating appropriate configurations as backgrounds, we derive the BFSS matrix theory and the IIB matrix model in the large N limit.
We consider backgrounds
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
where  and
and 
 (
( ) represent N points randomly distributed in a d-dimensional space. There are infinitely many such configurations.
) represent N points randomly distributed in a d-dimensional space. There are infinitely many such configurations.  represents an eleven-dimensional constant vector. By using SO(1,10) symmetry, we can choose (3) as a background without loss of generality.
represents an eleven-dimensional constant vector. By using SO(1,10) symmetry, we can choose (3) as a background without loss of generality.  will be identified with a coupling constant.
will be identified with a coupling constant.  corresponds to
corresponds to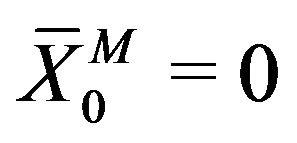 , which leads to SO(1,10) symmetric vacua.
, which leads to SO(1,10) symmetric vacua.
We assume all the backgrounds (1), (2), (3) and (4) as independent vacua and fix them in the large N limit [40]. Thus, we do not integrate ,
,  or the diagonal elements of
or the diagonal elements of  and we expand the fields around the backgrounds as,
and we expand the fields around the backgrounds as,
 (5)
(5)
where we impose a chirality condition
 (6)
(6)
Under these conditions, the first term of the action (5) is rewritten as
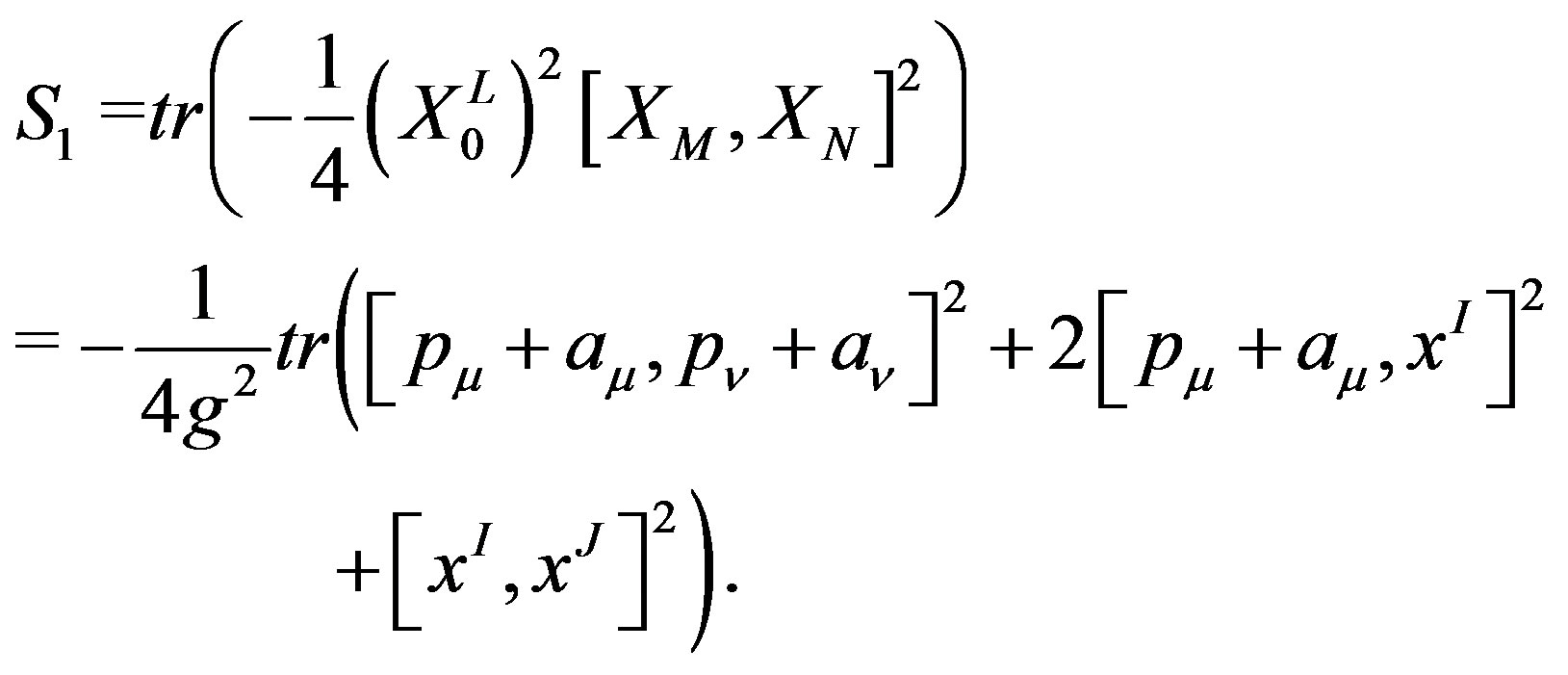 (7)
(7)
The second term is
 (8)
(8)
As a result, the total action is independent of  as follows,
as follows,
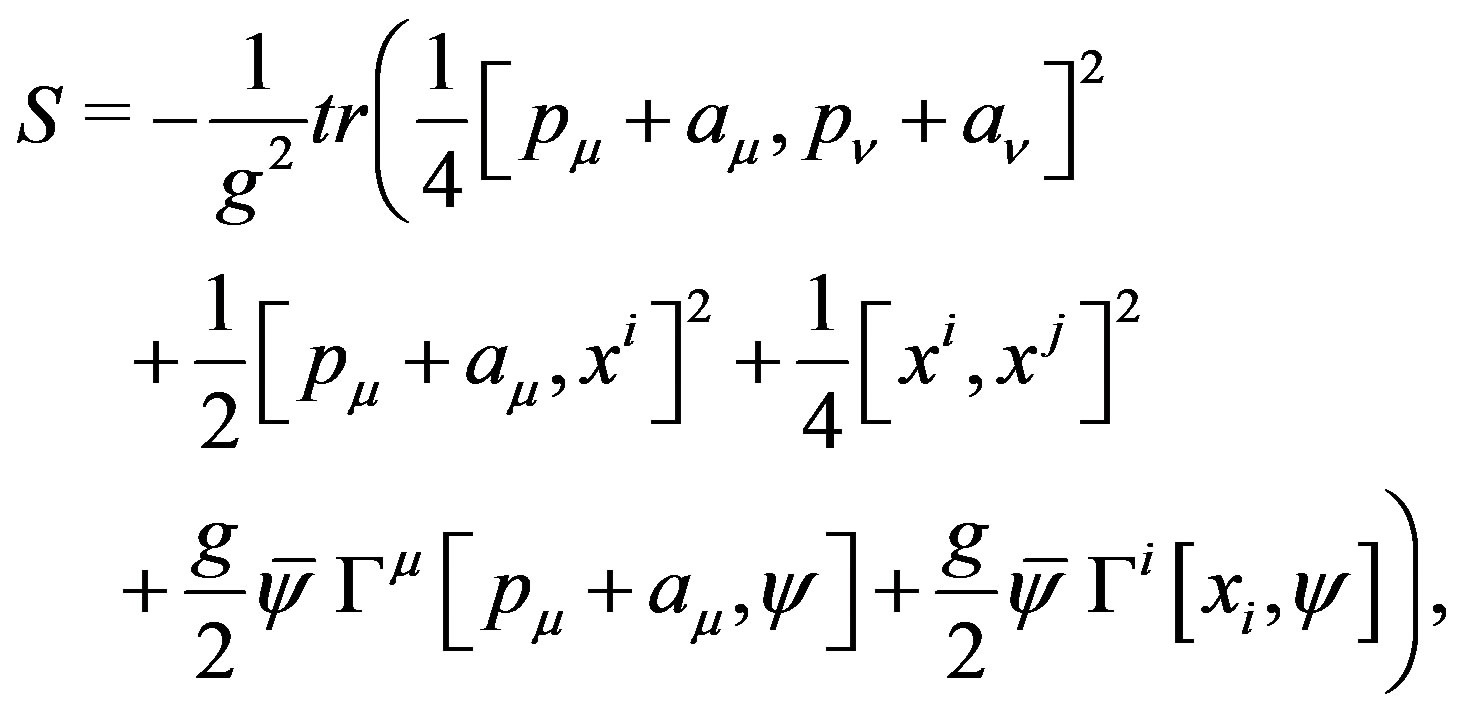 (9)
(9)
where . In the large N limit, this action is equivalent to
. In the large N limit, this action is equivalent to

where  is redefined to
is redefined to . This fact is proved perturbatively and non-perturbatively in the large N limit as in the case of the large N reduced model [41-44].
. This fact is proved perturbatively and non-perturbatively in the large N limit as in the case of the large N reduced model [41-44].
Under the conditions (1)-(6), the super transformations (8) and (10) reduces to



by which (9) is invariant. Moreover, (9) and (11) reduces to
 (10)
(10)
because the action (5) reduces to the action (9) and . This is consistent with the fact that
. This is consistent with the fact that  and
and  are fixed.
are fixed.
Therefore, if we choose the backgrounds with , we obtain the BFSS matrix theory in the large N limit,
, we obtain the BFSS matrix theory in the large N limit,
 (11)
(11)
If we choose those with , we obtain the IIB matrix model in the large N limit,
, we obtain the IIB matrix model in the large N limit,
 (12)
(12)
We also obtain matrix string theory [45-47] when 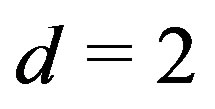 and
and  [48] when
[48] when .
.
4. Conclusion and Discussion
In this paper, we have studied a natural supersymmetric extension of the bosonic covariant 3-algebra model for M-theory proposed in [1]. It possesses manifest SO(1,10) symmetry. The action is invariant under 64 supersymmetry transformations, although the supersymmetry algebra does not close. In this model, the eleven-dimensional space-time is given by eigen values of the U(N) part of the bosonic fields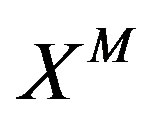 . From this action, by choosing appropriate vacua, we have derived the BFSS matrix theory and the IIB matrix model in a large N limit.
. From this action, by choosing appropriate vacua, we have derived the BFSS matrix theory and the IIB matrix model in a large N limit.
In order to obtain a covariant 3-algebra model for M-theory by means of a matrix regularization of a supermembrane action, the action must be written only with the Nambu brackets. Then, the action must be invariant under constant shifts of the fermions, that is under the kinematical supersymmetry transformations. The number of them is 32 because the Majorana fermions possess 32 components for covariance. Thus, the total number of the dynamical and kinematical supersymmetries exceeds the number of the  supersymmetries. Therefore, there does not exist a
supersymmetries. Therefore, there does not exist a  supersymmetric covariant 3-algebra model for M-theory that is obtained by a matrix regularization of a supermembrane action. As a result, there are two possibilities for 3-algebra models for Mtheory. One is a covariant 3-algebra model for M-theory that possesses more than 32 supersymmetries as in this paper. Another is a
supersymmetric covariant 3-algebra model for M-theory that is obtained by a matrix regularization of a supermembrane action. As a result, there are two possibilities for 3-algebra models for Mtheory. One is a covariant 3-algebra model for M-theory that possesses more than 32 supersymmetries as in this paper. Another is a  supersymmetric 3-algebra model for M-theory that is obtained by a matrix regularization of a non-covariant supermembrane action7.
supersymmetric 3-algebra model for M-theory that is obtained by a matrix regularization of a non-covariant supermembrane action7.
5. Acknowledgements
We would like to thank T. Asakawa, K. Hashimoto, N. Kamiya, H. Kunitomo, T. Matsuo, S. Moriyama, K. Murakami, J. Nishimura, S. Sasa, F. Sugino, T. Tada, S. Terashima, S. Watamura, K. Yoshida, and especially H. Kawai and A. Tsuchiya for valuable discussions.
NOTES
2A formulation of M-theory by a cubic matrix action was proposed by Smolin [32-34].
3This extension was originally proposed in Appendix of [1].
4Ghost-free Lorentzian 3-algebra theories were studied in [37,38].
5This fact was originally shown in [39].
6This kind of mechanism and interpretation was originally found in [35].
7In [49-51], because a supermembrane action that is 3-algebra manifest but a non-covariant, is obtained by fixing only the 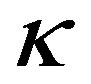 -symmetry of the covariant supermembrane action, it is expected to obtain all the physical observables in M-theory by using the corresponding 3-algebra model.
-symmetry of the covariant supermembrane action, it is expected to obtain all the physical observables in M-theory by using the corresponding 3-algebra model.