Harmonic excitation of linear respiratory mechanics for physiological dual controlled ventilation ()
1. INTRODUCTION
Dual controlled ventilation (DCV) is nowadays the most improved lung ventilation modality providing for controlled breathings to patients treated with anaesthesia (surgical) or in Intensive Care Units or affected by the respiratory insufficient syndrome. Unlike spontaneous breathings, i.e. breathings governed by the patient himself, controlled breathings are those for which the control of lung ventilation is completely achieved by an external device, the ventilator. The rationale of DCV can be easily understood by following the most relevant stages relative to the historical evolution of mechanical ventilation [1- 3].
Controlled ventilation (CV) is required when the spontaneous breathing of anaesthetized or severe brain injured patients is forbidden or absent. Therefore, CV includes all that modalities for which the respiratory pattern shows only controlled breathings in series with time.
When the clinical conditions of patient improve, spontaneous breathings appear even if at too much lower frequency or below the standard physiological level. In such situation, assisted/controlled ventilation (A/CV) is recommended. Allowing the patient the possibility of spontaneous breathing at his will or capability, AC/V includes all that modalities or techniques in which the ventilator supplies the patient with controlled breathing only after a long lasting interval of apnea (assisted ventilation) or at detection of a very weak effort of spontaneous breathing (synchronized or triggered ventilation). The respiratory pattern during A/CV shows both controlled and spontaneous breathings in random series with time [4].
The controlled breathings during CV or A/CV can be properly classified considering the primary physical parameters controlled during the inspiratory time irrespective of load (respiratory characteristics of patient) variations or fluctuations as well as ventilator settings [5,6].
In the two basic modalities of controlled breathings, consisting in volume-controlled ventilation (VCV) and pressure-controlled ventilation (PCV), the ventilator supplies the load (respiratory system of patient) with the pre-established tidal volume through the selected respiratory airflow waveform and applies to the load (respiratory system of patient) the pre-established airways pressure waveform, respectively [5-7].
DCV has been recently introduced in the clinical practice [8]. Before that, with the exception of neonatology, where PCV was preferred since low tidal volume computation and control are both too much critical [9], VCV was mainly adopted [10]. This condition was derived from the clinical assumption considering the control of tidal volume essential for ensuring an adequate clearance of CO2 in CV or A/CV modalities applied to adult patients [11]. Nowadays, on account of well established lower physiological character of VCV as well as its higher level of intrinsic pathological risk of “volotrauma”, i.e. alveolar over distension, specially for reduced lung compliance and of hypoxia, both due to functional failure of tidal volume computation, PCV is certainly the most adopted CV or A/CV modality for any kind of patient [12]. On the other hand, PCV, while eliminating the risk of “barotrauma” by measuring and controlling the airways pressure, can easily led to hypoxia for reduced tidal volume associated with high or increased inspiratory airways resistance [5-7].
DCV has been proposed in replay to the clinical requirement of a PCV with ensured tidal volume [13]. In detail, DCV is an advanced form of PCV in which the magnitude of selected airways pressure waveform is not kept constant but it is automatically regulated by feedback control for delivering during the inspiratory time either the tidal volume required or, considering the current respiratory frequency, the pre-established volume supplied to patient in every minute (minute volume) [6,7]. This is the so called DCV “breath to breath” mode, representing the most diffused form of DCV in the clinical practice [8,14]. In a different way, the so called DCV “within a breath” mode is a DCV in which the ventilator switches from pressure to volume control in the middle of the inspiratory time [8,14].
In most cases during CV or A/CV, the respiratory system of healthy anaesthetized or severe brain injured patients exhibits a steady and reproducible response to controlled breathings, if evaluated as a whole. Moreover, the respiratory dynamics involved is considerably reduced on account of small tidal volumes required. Therefore, the respiratory mechanics of such patients can be properly assumed steady and linear [6]. According to PCV excitation hypothesis along with to steady and linear respiratory mechanics assumption, only DCV “breath to breath” mode will be considered in the present work. Moreover, DCV “breath to breath” mode is perfectly compatible with the functional features of the Advanced Lung Ventilation System (ALVS) adopting a feedback control for the ventilation process which regulates the operative parameters only between different controlled breathings evaluated as a whole, i.e. in steady conditions and does not within the transient time of each breath [6, 7].
The present work deals with the description of both theory and ALVS settings required for applying to healty anaesthetized or severe brain injured patients harmonic waveforms as airways pressure excitation modality (HEM) and for the best control of DCV through the implementation of an improved diagnostic measurement procedure. Moreover, the results of software simulations, reproducing the real physiopathological and clinical conditions of such patients treated with CV or A/CV, will be reported and discussed.
2. METHODS
Among the different systems proposed for implementing DCV [5,15-20], ALVS exhibits the following suitable functional features [6,7]:
1) opportunity of applying any airways pressure waveform of clinical interest during the time of controlled breathing without distortions, i.e. identical to that selected;
2) insensitivity of selected airways pressure waveform in shape and intensity to the variations of respiratory parameters of patient and to the ventilator settings;
3) full-time compatibility of controlled breathings with spontaneous breathing activity of patient during continuous positive airways pressure (CPAP) or bilevel positive airways pressure (BiPAP) ventilation modalities and during A/CV, including also synchronized or triggered ventilation modalities;
4) more physiological shapes of respiratory and ventilation pattern waveforms unaffected by high slope variations or spikes;
5) improved diagnostic measurement procedure, avoiding the airflow interruption technique [21,22], for the determination of all the respiratory parameters useful in adapting ALVS settings to the clinical and physiological requirements of patient.
According to the shape and intensity of selected airways pressure waveform as well as to the current respiratory parameters of patient, available at the end of each controlled breathing from ALVS diagnostic procedure (point 5)), the points 1) and 2) are both performed by implementing the following two steps. The first step is carried out for the steady control of ventilation process during the time of apnea and consists in proper regulating the working pressure (PG) of ALVS generator as well as the equilibrium values associated with the adjustablesteady components (RG0, REXT0) of its internal (RG) and external (REXT) resistances. The second step is carried out for the transient control of ventilation process during the respiratory time of each controlled breathing and consists in proper modeling the time-varying components ( ,
, ) of RG and REXT. The points 3), 4) and 5) result from novel choices adopted in ALVS design, allowing the airways pressure increase/decrease during inspiration/expiration and static lung compliance measurement, respectively, to be performed maintaining continuous forever the airflow crossing the ventilation circuit from the generator to outside. In such a way, the absence of on-off valves acting on airflow eliminates any undesiderable artificial distortion affecting the respiratory and ventilation pattern waveforms occurring when the airflow is interrupted along the ventilation circuit during CV or A/ CV.
) of RG and REXT. The points 3), 4) and 5) result from novel choices adopted in ALVS design, allowing the airways pressure increase/decrease during inspiration/expiration and static lung compliance measurement, respectively, to be performed maintaining continuous forever the airflow crossing the ventilation circuit from the generator to outside. In such a way, the absence of on-off valves acting on airflow eliminates any undesiderable artificial distortion affecting the respiratory and ventilation pattern waveforms occurring when the airflow is interrupted along the ventilation circuit during CV or A/ CV.
The design and the functional features of ALVS have been extensively reported and discussed in a specific paper [6]. In summary, as shown in Figure 1, ALVS is made up of three main functional units properly connected among them at airways node (AW), which are implemented by the following devices:
1) airflow generator stabilizer (AGS);
2) airways pressure  waveform controller (APWC);
waveform controller (APWC);
3) respiratory system simulator (RSS).
The electric-equivalent network of ALVS is shown in Figure 2. AGS is achieved by means of an adjustablesteady pressure generator (PG) in series with an adjustable-steady (RG0) and a time-varying  components of its internal resistance (RG). So that, the waveform of
components of its internal resistance (RG). So that, the waveform of  is defined as follows:
is defined as follows:
 (1)
(1)
APWC consists of an external resistance (REXT), including its adjustable-steady component (REXT0) in series with its time-varying component , placed be-
, placed be-

Figure 1. The three main functional units assembled in the Advanced Lung Ventilation System (ALVS) for performing the harmonic excitation modality (HEM): airflow generator stabilizer (AGS), airways pressure waveform controller (APWC) and respiratory system simulator (RSS). AW denotes the airways node.

Figure 2. Overall electric-equivalent network of ALVS designed for HEM. AW denotes the airways node, while tilted arrows and sinusoidal symbols denote variable and time-varying components, respectively. The ground level corresponds to the atmospheric pressure. See text.
tween AW and ground, i.e. atmospheric pressure level. So that, the waveform of  is defined as follows:
is defined as follows:
 (2)
(2)
RSS includes a variable resistance (RP) connected in series with a variable elastic compliance (CP) simulating, respectively, the airways resistance and the static lung compliance of a wide variety of patients and pathologies. The model is adequate considering patients with homogeneous and steady respiratory characteristics when treated with CV or A/CV [23]. On account of the physiopathological and clinical condition of considered patients, i.e. healthy anaesthetized or severe brain injured patients, RSS adopts a steady and linear respiratory mechanics [24]. Consequently, two basic hypothesis can be assumed on ALVS and in particular, on RSS [6]. The first hypothesis consists in considering the drop of pressure (ΔP) across any fluidodynamic resistance (R) linearly dependent on airflow (Φ), according to the following relation:
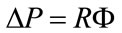 (3)
(3)
The second hypothesis consists in considering, over the whole duration of each single controlled breathing, the lung volume (VP) linearly dependent on endoalveolar pressure (PEA), as follows:
 (4)
(4)
With reference to the time interval inside each single controlled breathing, the relation (4) implies that the ratio between the waveform of  and of
and of  is not dependent on time but can be assumed constant, according to the following relation:
is not dependent on time but can be assumed constant, according to the following relation:
 (5)
(5)
Moreover, due to the physical characteristics of controlled breathings during CV or A/CV, ALVS works by feedback regulation acting after the acquisition of each controlled breathing accounted as a whole, i.e. in steady conditions. According to the assumption of linear respiratory mechanics for controlled breathings accounted as a whole, i.e. in steady conditions, the static lung compliance (CP) can be considered as constant during the whole respiration time, while the different values assumed by the airways resistance (RP) during inspiration, i.e. inspiratory airways resistance (RINS) and during expiration, i.e. expiratory airways resistance (REXP), can be both considered constant. Such physical model does not include any inductance, on account of negligible inertia of airflow as well as airways, lungs and chest tissues at very low respiratory frequencies involved [6,23,24].
ALVS settings required for reaching advanced square waveform as airways pressure excitation as well as the relative experimental results obtained with a proper lung simulator, have been reported in a first work [6]. Moreover, ALVS settings required for reaching advanced and more physiological triangular and trapezoidal waveforms as airways pressure excitation, have been reported in a subsequent recent work [7].
As synthesis and optimization of such previous path, the present paper presents and proposes harmonic waveforms as airways pressure excitation modality (HEM) applied by ALVS for controlled breathing approximating the physiological shape of transpulmonary pressure pattern. HEM is the best solution for inducing, during CV or A/CV, a really physiological reaction, i.e. respiratory airflow waveform of sinusoidal shape, on healthy anaesthetized or severe brain injured patients, whose respiretory mechanics can be properly assumed steady and linear. Moreover, an improved closed-loop diagnostic measurement procedure has been developed and implemented for the optimization of DCV “breath to breath” and for controlling tidal or minute volumes.
3. ALVS SETTING FOR HARMONIC EXCITATION MODALITY (HEM)
As introduced in §2, the optimization of the ventilation process is achieved by ALVS performing two independent but simultaneous procedures: the steady and the transient controls. According to the same formalism used for  and
and , the waveforms of
, the waveforms of , of
, of , of
, of  and of airflow crossing REXT, i.e. external airflow
and of airflow crossing REXT, i.e. external airflow , are defined as the result of the addition of their steady
, are defined as the result of the addition of their steady
 and time-varying
and time-varying
 components, as follows:
components, as follows:
 (6)
(6)
 (7)
(7)
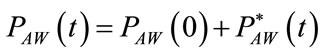 (8)
(8)
 (9)
(9)
3.1. Steady Control of Ventilation Process
The steady control is reached through the proper setting of PG as well as of adjustable-steady component of RG and REXT, i.e. RG0 and REXT0, respectively. The electricequivalent network of ALVS configuration actives for the steady control is shown in Figure 3.
During the stationary conditions occurring at the end of expiratory time of controlled breathings when PAW should be regulated on selected value of airways or external positive end expiratory pressure (PEEPEXT) as well as during apnea anticipating spontaneous breathings when PAW should be regulated on selected value of continous positive airways pressure (CPAP), the application of the first Kirchhoff’s law to the airways node (AW) of the network reported in Figure 3 leads to the following equations:
 (10)
(10)
 (11)
(11)
ΦRES and ΦVEN are the airflow crossing RP, i.e. the respiratory airflow and the airflow supplied by AGS, i.e. the ventilation airflow, respectively.
Therefore, during stationary conditions, AGS acts as an ideal airflow generator delivering to the airways node (AW) a stabilized airflow irrespective of load (REXT, RP, CP) variations or fluctuations, if both the following conditions are verified:
 (12)
(12)
 (13)
(13)
By the regulation of PG, RG0 and REXT0 under both the conditions (12) and (13), the following relations apply for independent control of the equilibrium value of ΦVEN (ΦVEN0) delivered by AGS in stationary conditions and PEEPEXT:

Figure 3. Electric-equivalent network of ALVS active for the steady control of ventilation process. See §3.1.
 (14)
(14)
 (15)
(15)
From (15), REXT0 results as follows:
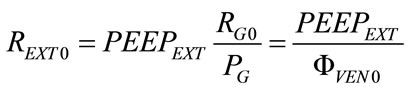 (16)
(16)
The end of expiratory time of previous controlled breathings as well as the end of apnea time anticipating spontaneous breathings correspond to the begin of current inspiratory time (t = 0). By inserting into (5) the condition t = 0 and considering (11), the following expression results for initial lung volume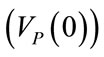 , i.e. functional residual capacity (FRC), endoalveolar or total positive end expiratory pressure (PEEPTOT) and steady component of ΦEXT (ΦEXT0):
, i.e. functional residual capacity (FRC), endoalveolar or total positive end expiratory pressure (PEEPTOT) and steady component of ΦEXT (ΦEXT0):
 (17)
(17)
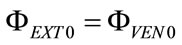 (18)
(18)
On account of (10), in (17) PEEPTOT is correctly assumed coincident to PEEPEXT.
3.2. Transient Control of Ventilation Process
The stationary conditions, just described in §3.1, represent the conditions occurring at the beginning of both spontaneous and controlled breathings. Once the steady control has been carried out according to §3.1, the transient control during the respiratory time of controlled breathing is reached through the proper modeling of time-varying component of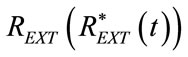 . The electric-equivalent network of ALVS configuration active for the transient control is shown in Figure 4.
. The electric-equivalent network of ALVS configuration active for the transient control is shown in Figure 4.
In order that AGS keeps ΦVEN stabilized on ΦVEN0 value during the respiratory time also, both the conditions (12) and (13) should be modified as follows:
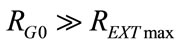 (19)
(19)
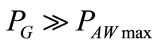 (20)
(20)
REXTmax and PAWmax are the maximum values assumed during respiratory time by REXT and PAW, respectively.
Inside each transient respiratory time during inspiration and expiration, ΦRES assumes the form of inspiratory airflow (ΦINS) and expiratory airflow (ΦEXP), respectively. According to their opposite directions, ΦINS and ΦEXP are conventionally assumed as positive and negative quantities, respectively.
The aim of the present work consists in determining, once PG, RG0 and REXT0 have been regulated on values
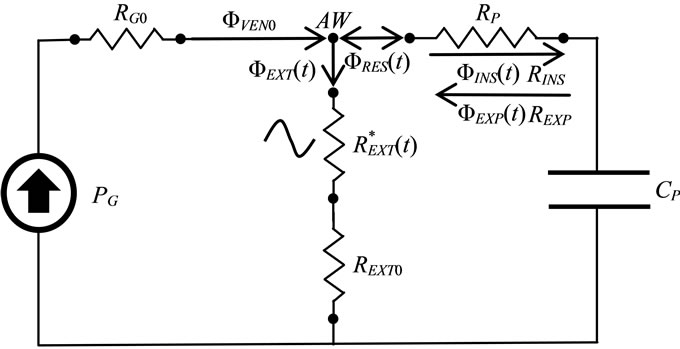
Figure 4. Electric-equivalent network of ALVS active for the transient control of ventilation process during HEM. See §3.2.
required for the steady control of both ΦVEN0 and PEEPEXT, the time-varying component of  with which the controlled breathing applied by ALVS to healty anaesthetized or severe brain injured patients, whose respiratory mechanics can be properly assumed steady and linear during CV or A/CV, shows a physiological pattern, i.e. a respiratory airflow waveform
with which the controlled breathing applied by ALVS to healty anaesthetized or severe brain injured patients, whose respiratory mechanics can be properly assumed steady and linear during CV or A/CV, shows a physiological pattern, i.e. a respiratory airflow waveform  of sinusoidal shape, as follows:
of sinusoidal shape, as follows:
 (21)
(21)
where Φ0, ω and t are the amplitude, angular frequency and time, respectively. Obviously, according to (14), PG and RG0 should be chosen so that ΦVEN0 results anyhow greater than the required Φ0, as follows:
 (22)
(22)
The respiratory time (TR), i.e. the time interval associated to each controlled breathing as a whole, equals the sum of the inspiratory time (TI) and expiratory time (TE), as follows:
 (23)
(23)
Concerning with the choice of TI and TE, the following relations are assumed:
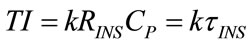 (24)
(24)
 (25)
(25)
The relations (24) and (25) establish that the same proportional coefficient (k) relates TI with the inspiratory time constant (τINS) and TE with the expiratory time constant (τEXP). So that, the following condition results:
 (26)
(26)
TR represents the time period of the respiratory process, being the reciprocal of the respiratory frequency (FR). TI, TE and TR are usually expressed in seconds, while FR in act for minute (act/min), according to the following relation:
 (27)
(27)
On account of different values generally required in the clinical practice for TI and TE, a sinusoidal shape of  associated to a controlled breathing lasting TR can be analytically defined by the following expressions:
associated to a controlled breathing lasting TR can be analytically defined by the following expressions:
 (28)
(28)
 (29)
(29)
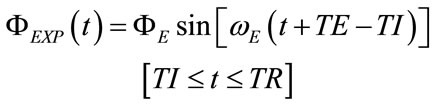 (30)
(30)
 (31)
(31)
 (32)
(32)
 and
and 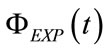 denote the waveforms of ΦINS and ΦEXP, respectively, while ωI and ωE are the inspiratory and expiratory angular frequencies, respectively.
denote the waveforms of ΦINS and ΦEXP, respectively, while ωI and ωE are the inspiratory and expiratory angular frequencies, respectively.
The integration of  over time from the beginning (t = 0) to the end (t = TR) of the controlled breathing should be equal to zero for accounting that the volume introduced inside lungs during inspiration, or inspiratory tidal volume (VTIDi), must be equal in magnitude and opposite in sign to the volume ejected during expiration, or expiratory tidal volume (VTIDe), as follows:
over time from the beginning (t = 0) to the end (t = TR) of the controlled breathing should be equal to zero for accounting that the volume introduced inside lungs during inspiration, or inspiratory tidal volume (VTIDi), must be equal in magnitude and opposite in sign to the volume ejected during expiration, or expiratory tidal volume (VTIDe), as follows:
 (33)
(33)
 (34)
(34)
On account of relations (28)-(32), the computation of (34) establishes the following condition:
 (35)
(35)
From (26), (31) and (32), the following condition results:
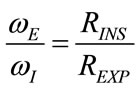 (36)
(36)
Considering the relations (6), (17), (28)-(32) and (35), the following expressions result:
 (37)
(37)
 (38)
(38)
 (39)
(39)
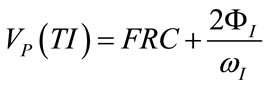 (40)
(40)
 (41)
(41)
 (42)
(42)
 (43)
(43)
 (44)
(44)
 (45)
(45)
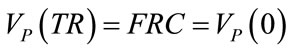 (46)
(46)
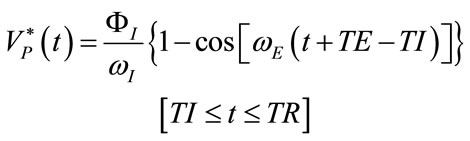 (47)
(47)
 (48)
(48)
 (49)
(49)
The minute volume (VMIN), i.e. the volume delivered to the patient for each minute, can be obtained as the product of respiratory frequency expressed in acts for minute (FR) with tidal volume expressed in litres (VTID), so that, considering (27), (36) and (43), VMIN results as follows:
 (50)
(50)
From (50) it is evident that VMIN depends only on ΦI and the ratio between expiratory and inspiratory airways resistances .
.
From (5), (7), (17), (39)-(42) and (45)-(48), the following expressions result:
 (51)
(51)
 (52)
(52)
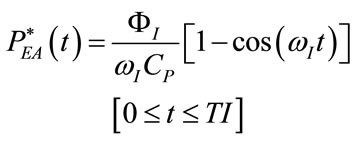 (53)
(53)
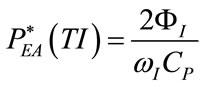 (54)
(54)
 (55)
(55)
 (56)
(56)
 (57)
(57)
 (58)
(58)
PEAmax appearing in the (52) is the maximum value assumed by PEA during respiratory time.
From the network shown in Figure 4 along with (28)- (32), (36) and (51)-(58), the following expressions result:
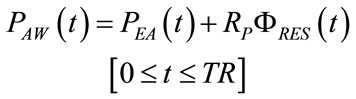 (59)
(59)
 (60)
(60)
 (61)
(61)
 (62)
(62)
 (63)
(63)
 (64)
(64)
 (65)
(65)
 (66)
(66)
 (67)
(67)
The studying of the algebric sign of time derivation of (60) provides for the determination of time intervals during inspiration associated with increasing or decreasing  function and in particular, of the time (tPmax) at which PAW assumes its maximum value (PAWmax), as follows:
function and in particular, of the time (tPmax) at which PAW assumes its maximum value (PAWmax), as follows:
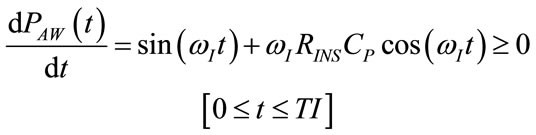 (68)
(68)
 (69)
(69)
On account of selected ωI as well as inspiratory parameters of patient (RINS, CP), the relation (69) establishes that tPmax occurs in the second half of inspiratory time, according to the following expression:
 (70)
(70)
PAWmax, depending on PEEPEXT, ΦI, ωI, RINS and CP, can be obtained by inserting the condition (69) into (60), as follows:
 (71)
(71)
The studying of the algebric sign of time derivation of (64) provides for the determination of time intervals during expiration associated with increasing or decreasing  function and in particular, of the time (tPmin) at which PAW assumes its minimum value (PAWmin), as follows:
function and in particular, of the time (tPmin) at which PAW assumes its minimum value (PAWmin), as follows:
 (72)
(72)
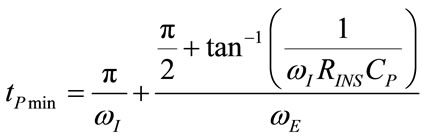 (73)
(73)
On account of selected ωI and ωE as well as inspiratory parameters of patient (RINS, CP), the relation (73) establishes that tPmin occurs in the second half of expiratory time, according to the following expression:
 (74)
(74)
PAWmin, depending on PEEPEXT, ΦI, ωI, RINS and CP, can be obtained by inserting the condition (73) into (64), as follows:
 (75)
(75)
In order to avoid PAWmin assumes negative value, corresponding to pressure below atmospheric level which would require impracticable negative values of REXT, the following condition derives from (43) and (75):
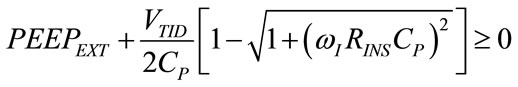 (76)
(76)
The studying of the algebric sign of time derivation of (68) and (72) provides for the determination of time intervals associated with positive or negative concavity of PAW(t) function and in particular, of the time at which flex points of PAW occur (PAWfleI, PAWfleE) during inspiration (tPfleI) and expiration (tPfleE), as follows:
 (77)
(77)
 (78)
(78)
 (79)
(79)
 (80)
(80)
On account of selected ωI and ωE as well as inspiratory parameters of patient (RINS, CP), the relations (78) and (80) establish that tfleI and tfleE occur in the first half of inspiratory and expiratory times, respectively, according to the following expressions:
 (81)
(81)
 (82)
(82)
The application of the first Kirchhoff’s law to the airways node (AW) of the network reported in Figure 4 leads to the following equation:
 (83)
(83)
From (9), (18) and (83), the following relation results:
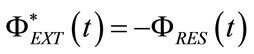 (84)
(84)
The application of the second Kirchhoff’s law to the APWC branch (AW-ground line) of the network reported in Figure 4 leads to the following equation:
 (85)
(85)
From (2), (16), (28)-(32), (35), (60), (64), (83) and (85), the following expressions result:
 (86)
(86)
 (87)
(87)
 (88)
(88)
 (89)
(89)
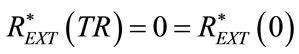 (90)
(90)
The time (tRzero) at which  crosses the line of zero during expiration and from (2), consequently,
crosses the line of zero during expiration and from (2), consequently,  crosses the line of REXT0, can be obtained by making equal to zero the numerator of (89), as follows:
crosses the line of REXT0, can be obtained by making equal to zero the numerator of (89), as follows:
 (91)
(91)
The studying of the algebric sign of time derivation of (87) and (89) provides for the determination of time intervals associated with increasing or decreasing  function and in particular, of the time at which
function and in particular, of the time at which 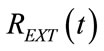 assumes its maximum value (REXTmax) during inspiration (tRmax) and its minimum value (REXTmin) during expiration (tRmin), as follows:
assumes its maximum value (REXTmax) during inspiration (tRmax) and its minimum value (REXTmin) during expiration (tRmin), as follows:
 (92)
(92)
 (93)
(93)
 (94)
(94)
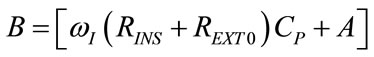 (95)
(95)
Considering that A and REXT0 are both positive quantities, so that B results greater that the term appearing as coefficient factor of cosine function (ωI RINS CP) in both (68) and (72), by comparison of (92) with (68) and of (93) with (72), it is easy to demonstrate that, according to the causality principle, i.e. the relation between cause and effect, REXTmax and REXTmin occur in time advanceof PAWmax and PAWmin, respectively, as follows:
 (96)
(96)
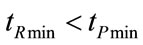 (97)
(97)
The determination of tRmax, tRmin, REXTmax and REXTmin, along with other features of  waveform, will be find out in §4, where the optimal relation between TI and τINS as well as between TE and τEXP will be established.
waveform, will be find out in §4, where the optimal relation between TI and τINS as well as between TE and τEXP will be established.
3.3. Diagnostic Measurement Procedures
The importance of determining the diagnostic parameters associated to the respiratory mechanics of patient during the ventilation treatment is well established [25-27].
In order to achieve a 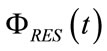 of sinusoidal shape for the current controlled breathing, the modeling of
of sinusoidal shape for the current controlled breathing, the modeling of  by means of both (87) and (89) requires the knowledge in advance of the respiratory parameters of patient (RINS, REXP, CP), which can be detected from the last monitored controlled breathing.
by means of both (87) and (89) requires the knowledge in advance of the respiratory parameters of patient (RINS, REXP, CP), which can be detected from the last monitored controlled breathing.
The best way to evaluate the preliminary value of the respiratory parameters of patient consists in applying a conventional square waveform as airways pressure excitation at the beginning of ventilation treatment. As described elsewhere [6], ALVS performs such excitation by switching REXT between two different values, the higher and lower of which are kept during inspiratory (TI) and expiratory (TE) times, respectively. For diagnostic purpose, the higher and lower levels of REXT should be kept at least for the time required to observe a ninety nine per cent (99%) reduction of inspiratory and expiratory airflows, respectively, with regard to their peak values. At the end of both such transient times, on account of zero respiratory airflow, the monitored values of PAW equal those assumed by PEA, providing for the determination of both the maximum (PEAmax) or peak endoalveolar pressure (PAP) and minimum (PEAmin) or total positive end expiratory pressure (PEEPTOT). The integration of monitored respiratory airflow during such inspiratory or expiratory transient times gives the tidal volume (VTID). Once PAP, PEEPTOT and VTID have been determined like this, CP results as follows:
 (98)
(98)
Considering that the monitored inspiratory (ITT) and expiratory (ETT) transient times are equal to five times τINS and τEXP, respectively, from (24) and (25), RINS and REXP can be determined as follows:
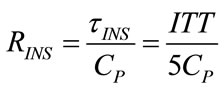 (99)
(99)
 (100)
(100)
Due to the application of uncompensated square waveform of PAW, the values of RINS and REXP obtained from (99) and (100), respectively, result both overestimated since ITT and ETT are slight longer than the real ones [6]. The error on RINS and REXP can be tolerated considering the preliminary character of such evaluation. The preliminary diagnostic procedure should be kept for a time corresponding to at least 20 subsequent controlled breathings, allowing a proper statistical evaluation of the results.
Once the preliminary values of RINS, REXP and CP have been estimated as just described, on account of (26), (31), (32), (35) and (36), the implementation of both (87) and (89) establishes the presence of HEM.
During the ventilation treatment with HEM, the variations or fluctuations of the respiratory parameters of patient can be detected at the end of each controlled breathing, providing for optimal control of the ventilation process during the following breathing. An improved diagnostic measurement procedure implemented for determining the current respiratory parameters of patient is based on the evaluation of the impedance (Z) associated with the electric-equivalent circuit of the respiratory system of patient (RSS, Figure 2) [28,29]. During the inspiratory time, Z assumes the following expression:
 (101)
(101)
The complex quantity Z can be represented as a vector in the complex plane, i.e. in polar coordinates, with module (ρ) and phase angle (θ) given by the following expressions:
 (102)
(102)
 (103)
(103)
By matching (102) and (103), RINS and CP result as follows:
 (104)
(104)
 (105)
(105)
From the theory of electric circuits with harmonic excitation, ρ can be related to the ratio between the amplitudes of 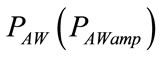 and
and 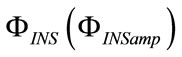 waveforms
waveforms , while θ to their phase displacement (δ), assumed positive when
, while θ to their phase displacement (δ), assumed positive when  occurs in advance of ΦINS(t), as follows:
occurs in advance of ΦINS(t), as follows:
 (106)
(106)
 (107)
(107)
In addition, considering that PAWamp can be deduced from peak-to-peak of  and from (29), the following relations result:
and from (29), the following relations result:
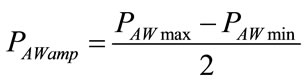 (108)
(108)
 (109)
(109)
Introducing (106), (107), (108) and (109) into (104) and (105), the following expressions result:
 (110)
(110)
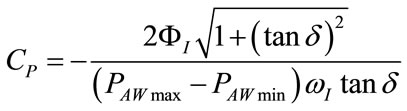 (111)
(111)
RINS and CP can be both determined at the end of each controlled breathing by means of (110) and (111) since PAWmax, PAWmin, ΦI, δ and ωI are all quantities easily deducible from monitoring patterns. The rightness of (110) and (111) can be verified by inserting (71) and (75) into themselves.
According to (98), an alternative way for the determination of CP is based on the application of (5) between the end and the beginning of inspiratory time, as follows:
 (112)
(112)
Again, PAP and PEEPTOT are both deducible from monitoring patterns, since they equal the values assumed by PAW in the final  and initial
and initial  instants of inspiratory time when ΦRES is zero, while VTIDi, according to (43), can be determined as the result of the time integration of the monitored
instants of inspiratory time when ΦRES is zero, while VTIDi, according to (43), can be determined as the result of the time integration of the monitored  during the whole inspiratory time (TI). The rightness of (112) can be verified by inserting (43) and (52) into itself. Finally, once RINS has been determined by means of (110), REXP can be obtained from (36) evaluating the ratio between ωI and ωE, both deducible from monitoring patterns.
during the whole inspiratory time (TI). The rightness of (112) can be verified by inserting (43) and (52) into itself. Finally, once RINS has been determined by means of (110), REXP can be obtained from (36) evaluating the ratio between ωI and ωE, both deducible from monitoring patterns.
4. RESULTS AND DISCUSSION
In order to check the validity of the treatment developed for HEM, the results obtained in §3 have been software implemented. MATLAB platform has been employed for providing the most significant functions of time, i.e. the waveform of respiratory and ventilation quantities or parameters as well as of time-varying devices regulating and controlling the process.
4.1. Preliminary Settings of the Model
Among the physical characteristics of harmonic excitation functions, the angular frequency (ω) is the most important to be properly set, according to the diagnostic parameters as inspiratory (τNS) and expiratory (τEXP) time constants. If ω and hence FR is too high, the resulting VTID is too small applying also the maximum value of PAWmax excluding the risk of “barotrauma”. If ω and hence FR is too low, the resulting VMIN is too small supplying also the maximum value of VTID excluding the risk of “volotrauma”. So that, the right choice is to set ω equal to the reciprocal of the respiratory time constant (τ) of patient, as follows:
 (113)
(113)
From (113), (24), (25), (31) and (32), the following relations result:
 (114)
(114)
 (115)
(115)
 (116)
(116)
 (117)
(117)
 (118)
(118)
Considering (103) along with the set (113)-(118), (43), (52), (61), (69), (71), (73), (75), (76), (78), (80), (91), (107), (110) and (111) assume the following expressions, respectively:
 (119)
(119)
 (120)
(120)
 (121)
(121)
 (122)
(122)
 (123)
(123)
 (124)
(124)
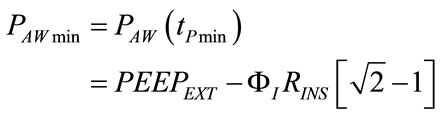 (125)
(125)
 (126)
(126)
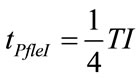 (127)
(127)
 (128)
(128)
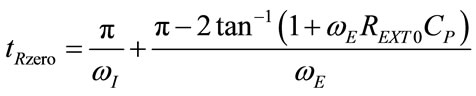 (129)
(129)
 (130)
(130)
 (131)
(131)
 (132)
(132)
Moreover, once RINS has been determined by means of (131), REXP can be obtained from (36), as follows:
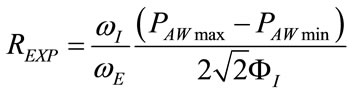 (133)
(133)
According to (120) and (123), the component of PAWmax above PEEPEXT shows a 21% increase in comparison with the same component of PEAmax.
4.2. Synthesis of Airways Pressure Waveform Controller (APWC)
As introduced in §2 and established in §3, APWC should be synthetized providing for both controlled and spontaneous breathings. Controlled breathings during CV or A/CV require the regulation and the modeling of 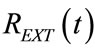 according to (2), (87) and (89), while spontaneous breathing during CPAP or BiPAP ventilation modalities require the regulation of REXT0, only according to (16). Moreover, for highest safety of patient, REXT should be quickly set to zero during any time of ventilation. The electric-equivalent network of APWC which implements
according to (2), (87) and (89), while spontaneous breathing during CPAP or BiPAP ventilation modalities require the regulation of REXT0, only according to (16). Moreover, for highest safety of patient, REXT should be quickly set to zero during any time of ventilation. The electric-equivalent network of APWC which implements  is shown in Figure 5.
is shown in Figure 5.
The safety procedure for fast discharge is ensured placing the switch S1 on position A, while the switch S2 is in any position. Proper conditions for apnea and for spontaneous breathings during CPAP or BiPAP ventilation modalities occur keeping for all the time of ventilation S1 and S2 on position I and M, respectively. Proper conditions for controlled breathings with HEM during CV or A/CV occur keeping S2 on position N, while cycling S1 between positions I and E kept during inspiratory and expiratory times, respectively. Proper conditions for triggered breathings during synchronized ventilation modalities occur keeping S1 and S2 on positions according to spontaneous breathings up to the time of trigger detection and after that, placing S1 and S2 on the positions according to controlled breathings.
4.3. Software Simulations
As described in §1, the optimal solution for both physiopathological and engineering controls of DCV should

Figure 5. Electric-equivalent network of airways pressure waveform controller (APWC). During apnea or for spontaneous breathings during CPAP or BiPAP ventilation modalities, the switches S1 and S2 are fixed on I and M positions, respectively. For controlled breathings with HEM during CV or A/CV modalities, S1 cycles between I and E positions kept during inspiratory and expiratory times, respectively, while S2 is fixed on N position. Proper conditions for triggered breathings during synchronized ventilation modalities occur keeping S1 and S2 on positions according to spontaneous breathings up to the time of trigger detection and after that, placing S1 and S2 on the positions according to controlled breathings. The safety procedure for fast discharge can be actuated placing S1 on A position, while S2 is on any position. See §4.2.
provide for the intrinsic advantages of both VCV and PCV, so that an adequate clearance of CO2 is ensured avoiding at the same time the risk of “volotrauma”. The functional parameters mainly related to the level of the clearance of CO2 and of the risk of “volotrauma” are the minimum required  and the maximum attainable
and the maximum attainable , respectively. As reference, for adult and neonatal patients,
, respectively. As reference, for adult and neonatal patients,  has been set to 4 and 0.4 liters for minute, respectively, while
has been set to 4 and 0.4 liters for minute, respectively, while  to the product of CP with 16 and 4 cmH2O, respectively. In order to regulate PEEPEXT on the optimal value by means of (17), FRC results as inversely proportional to the current value of τINS in addition to a constant value. Moreover, PEEPEXT can be slightly corrected according to (126). Finally, ΦVEN0 has been set to 2 and 0.2 liters for second for adult and neonatal patients, respectively.
to the product of CP with 16 and 4 cmH2O, respectively. In order to regulate PEEPEXT on the optimal value by means of (17), FRC results as inversely proportional to the current value of τINS in addition to a constant value. Moreover, PEEPEXT can be slightly corrected according to (126). Finally, ΦVEN0 has been set to 2 and 0.2 liters for second for adult and neonatal patients, respectively.
The first simulation assumes as initial input respiratory parameters the following ones, obtained at the end of the preliminary diagnostic procedure: RINS = 12.000 cmH2O/ l/s; REXP = 24.000 cmH20/l/s; CP = 0.0400 l/cmH2O. Such values are typical of an adult intubated surgical healthy patient (AP_1). The output results of the implementation of all the equations obtained in §3, together with the conditions established so far in §4, are shown in Figures 6-10, where the time waveforms of most significant functions concerning both respiratory and ventilation patterns

Figure 6. Time waveforms, one controlled breathing long, of respiratory airflow (ΦRES(t), red line) and of external airflow (ΦEXT(t), green line), obtained as outputs from software simulations implementing HEM applied to a typical adult surgical patient (AP_1, Table 1) with linear and steady respiratory mechanics. The levels of zero airflow and of ventilation airflow (ΦVEN0) are reported with black and blue dashed lines, respectively.
are reported one controlled breathing long. Figure 6 shows  and
and  functions with the levels
functions with the levels

Figure 7. Time waveforms, one controlled breathing long, of total lung volume (VP(t), blue line) and of lung volume above the functional residual capacity (FRC) level ( (t), red line), obtained as outputs from software simulations implementing HEM applied to a typical adult surgical patient (AP_1, Table 1) with linear and steady respiratory mechanics. The levels of FRC and of tidal volume (VTID) are reported with blue and red dashed lines, respectively.
(t), red line), obtained as outputs from software simulations implementing HEM applied to a typical adult surgical patient (AP_1, Table 1) with linear and steady respiratory mechanics. The levels of FRC and of tidal volume (VTID) are reported with blue and red dashed lines, respectively.

Figure 8. Time waveforms, one controlled breathing long, of airways pressure (PAW(t), green line) and of endoalveolar pressure (PEA(t), red line), obtained as outputs from software simulations implementing HEM applied to a typical adult surgical patient (AP_1, Table 1) with linear and steady respiratory mechanics. The level of external positive end expiratory pressure (PEEPEXT) is reported with blue dashed line.
of zero and of ΦVEN0. Figure 7 shows  and
and  functions with the levels of FRC and of resulting VTID. Figure 8 shows
functions with the levels of FRC and of resulting VTID. Figure 8 shows  and
and  functions with the level of PEEPEXT. Figure 9 shows
functions with the level of PEEPEXT. Figure 9 shows  function with the level of REXT0. Figure 10 shows the functions of external resistances appearing in the network of Figure 5 as time-varying resistance of APWC which, according to (87) and (89), have to be applied during inspiratory and
function with the level of REXT0. Figure 10 shows the functions of external resistances appearing in the network of Figure 5 as time-varying resistance of APWC which, according to (87) and (89), have to be applied during inspiratory and

Figure 9. Time waveform, one controlled breathing long, of external resistance (REXT(t), red line) implemented by APWC (Figure 5), obtained as outputs from software simulations implementing HEM applied to a typical adult surgical patient (AP_1, Table 1) with linear and steady respiratory mechanics. The equilibrium level of external resistance (REXT0) is reported with black dashed line.
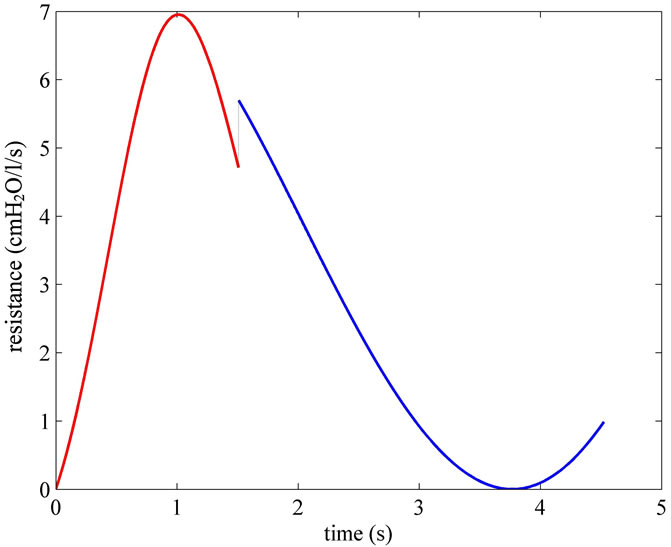
Figure 10. Time waveforms of external resistance (REXT(t)) above REXT0 (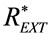 (t), red line) and above REXTmin (
(t), red line) and above REXTmin (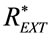 (t) + REXT0 − REXTmin, blue line), appearing in the network of Figure 5 as time-varying resistance of APWC, active during inspiratory (Equation (87)) and expiratory (Equation (89)) times, respectively, for implementing HEM applied to a typical adult surgical patient (AP_1, Table 1). The black dotted segment fills the discontinuity equals to the difference between REXT0 and REXTmin. See §3.2, §4.2 and §4.3.
(t) + REXT0 − REXTmin, blue line), appearing in the network of Figure 5 as time-varying resistance of APWC, active during inspiratory (Equation (87)) and expiratory (Equation (89)) times, respectively, for implementing HEM applied to a typical adult surgical patient (AP_1, Table 1). The black dotted segment fills the discontinuity equals to the difference between REXT0 and REXTmin. See §3.2, §4.2 and §4.3.
expiratory times, respectively, for performing HEM. All the functions reported in Figures 6-10 confirm that the implementation of both (87) and (89) produces ventilation and respiratory pattern waveforms with a real harmonic behaviour.
The value of most significant parameters pre-set as input and resulting as output of software simulation are reported in Table 1. For testing the ability of HEM in adapting to changed conditions occurring during the ventilation treatment, the following pathological processes have been considered:
1) increased airways resistance (AP_2);
2) reduced lung compliance (AP_3);
3) coincidence of 1) and 2) (AP_4).
The results of such further simulations are also reported in Table 1.
The second simulation assumes as initial input respiratory parameters the following ones, obtained at the end
of the preliminary diagnostic procedure: RINS = 40.000 cmH2O/l/s; REXP = 80.000 cmH2O/l/s; CP = 0.0025 l/cmH2O. Such values are typical of a neonatal intubated healthy patient (NP_1). The value of most significant parameters pre-set as input and resulting as output of software simulation are reported in Table 2, which includes the same pathological processes considered for adult patient (NP_2, NP_3, NP_4).
The waveforms shown in Figures 6-10 and the data reported in Tables 1-2 are both in full agreement with the results achieved in §3. Going into particulars, the waveforms of respiratory airflow , lung volume
, lung volume
 , endoalveolar pressure
, endoalveolar pressure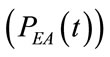 , airways pressure
, airways pressure  and external resistence
and external resistence 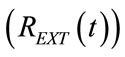 are all of sinusoidal shape, according to harmonic excitation modality (HEM). Expiratory angular frequency (ωE) is not coincident with inspiratory angular frequency (ωI), on account of different expiratory (TE) and inspiratory (TI) times. TI and TE are set equal to the product of π with expiratory (τEXP) and inspiratory (τINS) time constants, respectively, providing for their best adaptation to the current value assumed by the respiratory parameters of patient during the ventilation treatment. The values of TI, TE, FR, FRC, VTID and VMIN reported in Tables 1-2 are all consistent with the clinical requirement relative to considered patient (adult or newborn) with specific physiopathological respiratory conditions. Moreover, the amplitudes of inspiratory (ΦI) and expiratory (ΦE) airflow waveforms as well as minimum (PEAmin, PAWmin) and maximum (PEAmax, PAWmax) endoalveolar and airways pressures fit well the clinical requirements for both adult and neonatal patients [3,9].
are all of sinusoidal shape, according to harmonic excitation modality (HEM). Expiratory angular frequency (ωE) is not coincident with inspiratory angular frequency (ωI), on account of different expiratory (TE) and inspiratory (TI) times. TI and TE are set equal to the product of π with expiratory (τEXP) and inspiratory (τINS) time constants, respectively, providing for their best adaptation to the current value assumed by the respiratory parameters of patient during the ventilation treatment. The values of TI, TE, FR, FRC, VTID and VMIN reported in Tables 1-2 are all consistent with the clinical requirement relative to considered patient (adult or newborn) with specific physiopathological respiratory conditions. Moreover, the amplitudes of inspiratory (ΦI) and expiratory (ΦE) airflow waveforms as well as minimum (PEAmin, PAWmin) and maximum (PEAmax, PAWmax) endoalveolar and airways pressures fit well the clinical requirements for both adult and neonatal patients [3,9].
In current ventilators employed in the clinical practice for controlled breathing, VCV or PCV are mainly implemented with constant inspiratory airflow or airways pressure, respectively [6]. Occasionally, waveforms with slightly increased shape are adopted in DCV [8,12]. Such strong limitation in waveform modeling of physical parameters controlled by the ventilator, resulting from simplified hardware and software design, reduces drastically the functional versatility of the ventilator performances. As a result, among the wide variety of waveforms potentially applicable to the patient treated with A/CV, waveforms with very low physiological profile are the only one practically adopted in the clinical environment. Besides, such conventional waveforms are systematically and unpredictably altered in shape and intensity, due to its strong dependence on load (respiratory characteristics of patient) variations or fluctuations and on ventilator settings [4,6,7].
So that, the application of waveforms with increased physiological shape, i.e. sinusoidal waveforms, insensitive to load variations and ventilator settings, which automatically adapt themselves to the current value of respiratory parameters of patient and perform the control of lung volume “breath to breath”, would definitively solve the problem of optimizing DCV [7,13]. The result of the present study show clearly that HEM implemented by properly designed ALVS provides for such opportunity.
5. CONCLUSIONS
According to the clinical requirement asking for a dual controlled ventilation (DCV) with physiological respiratory and ventilation pattern as well as feedback control accounting the diagnostic evolution, i.e. the current value of respiratory parameters of patient, the advanced lung ventilation system (ALVS) has been improved for including harmonic excitation modality (HEM) in its functional features. HEM can be obtained with the design of the airways pressure waveform controller (APWC) implementing a pre-established waveform of the external resistance , whose optimization is achieved by means of an improved diagnostic measurement procedure available from the monitoring system. Moreover, APWC makes also compatible the controlled breathings with spontaneous breathings activity of patient during continuous positive airways pressure (CPAP) or bilevel positive airways pressure (BiPAP) ventilation modalities and during assisted/controlled ventilation (A/CV), including also synchronized or triggered ventilation modalities, ensuring the highest level of safety for patient in any conditions.
, whose optimization is achieved by means of an improved diagnostic measurement procedure available from the monitoring system. Moreover, APWC makes also compatible the controlled breathings with spontaneous breathings activity of patient during continuous positive airways pressure (CPAP) or bilevel positive airways pressure (BiPAP) ventilation modalities and during assisted/controlled ventilation (A/CV), including also synchronized or triggered ventilation modalities, ensuring the highest level of safety for patient in any conditions.
If applied to patients treated with anaesthesia or in Intensive Care Units or affected by respiratory distress syndrome, whose respiratory mechanics can be assumed steady and linear, HEM shows the expected optimal performances for both clinical and engineering point of view.
The waveforms and the data produced by software simulations (§4.3) are completely consistent with the overall results obtained by the theoretical treatment (§3). In particular, according to HEM, the respiratory and ventilation pattern waveforms are all of sinusoidal shape with expiratory angular frequency (ωE) different from inspiratory angular frequency (ωI), both according to expiratory (TE) and inspiratory (TI) times, which are set equal to the product of π with expiratory (τEXP) and inspiratory (τINS) time constants, respectively. This choice represents the best solution for adapting TI and TE to the current value assumed by the respiratory parameters of patient during the ventilation treatment.
HEM belongs to the DCV “breath to breath” modalities since it consists in applying a sinusoidal and hence physiological PCV excitation waveform along with feedback control of pre-selected tidal volume at the end of each breathing. PCV excitation avoids the risk of “volotrauma”, i.e. alveolar over distension, while the control of lung volume ensures an adequate clearance of CO2. The feedback control of tidal or/and minute volume is performed regulating the amplitude of external resistance waveform 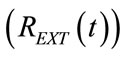 which is properly modeled according to the current value of the respiratory parameters of patient.
which is properly modeled according to the current value of the respiratory parameters of patient.
The system design has been developed in order to eliminate any airflow interruption along the ventilation circuit during CV or A/CV, otherwise required for performing the airways pressure increase/decrease during inspiration/expiration as well as the static lung compliance measurement. Maintaining continuous forever the airflow crossing the ventilation circuit from the pneumatic generator to outside provides for the following useful functional features:
1) elimination of any undesiderable artificial distortion affecting the respiratory and ventilation pattern waveforms;
2) full-time compatibility of controlled breathings with spontaneous breathing activity of patient during continuous positive airways pressure (CPAP) or bilevel positive airways pressure (BiPAP) ventilation modalities and during A/CV, including also synchronized or triggered ventilation modalities.
Moreover, an improved diagnostic measurement procedure performs at the end of each controlled breathing the determination of all the relevant respiretory parameters of patient as inspiratory and expiratory airways resistances together with static and dynamic lung compliance. The airflow interruption technique is not required for measuring the maximum or peak (PAP) and minimum or total positive end expiratory pressure (PEEPTOT) values assumed by endoalveolar pressure as well as static lung compliance, since the sinusoidal shape of respiratory airflow waveform  brings about the coincidence of the value assumed by endoalveolar pressure (PEA) with those assumed by monitored airways pressure (PAW) at the beginning and end of inspiration time, where ΦRES is zero.
brings about the coincidence of the value assumed by endoalveolar pressure (PEA) with those assumed by monitored airways pressure (PAW) at the beginning and end of inspiration time, where ΦRES is zero.
In conclusion, the results of the present work shows that HEM offers the best performance for an optimal and physiological control of DCV, establishing the rationale for specific laboratory and clinical tests.