The Fractional Hydrogen Atom: A Paradigm for Astrophysical Phenomena ()
1. Introduction
Bohr put forward the postulates that lead to the emergence of the hydrogen atom. The orbital angular momentum is quantized and that atomic emission is possible only when an electron makes a transition form a higher level to a lower one. Moreover, the orbit, velocity and energy of the electron are quantized in terms of the principal quantum number n that takes integer values. Under high pressure the hydrogen atom is transformed in a system of degenerate electron gas. This state is identified astrophysically as a white dwarf. White dwarfs are studied by Chandreshekar [1] who set a limit to their existence as stable stars. Investigation of white dwarfs provides important constraints on the theory of stellar evolution. If more pressure is applied on the hydrogen atom, a new state of neutrons results in. This new state of hydrogen is known as neutron stars. If more pressure is applied a final state of black hole is reach that not even light can escape from. The electron and neutron gases are described statistically by Fermi-Dirac distribution. However, the neutron gas provides a large pressure than the electron gas. The neutron gas can withstand more gravity than electron gas does.
The state of hydrogen atom under this high compression has not been provided by Bohr theory. In Bohr theory, the electron can only exist in certain orbits from the nucleus. The closest (minimum) one from the nucleus is the Bohr orbit. It amounts to a0 = 0.53 Å. Orbit quantization does not permit a lower orbit than this value. The question posed is that how can electron exist under high pressure? Bohr theory does not provide an answer to this question.
Recently, Arbab [2] has considered the effect of the internal magnetic field resulting from the electronic orbital current, and shown that this field is equivalent to considering a Bohr orbit with a fractional value of . In particular, this corresponds to,
. In particular, this corresponds to,  , where
, where  is the fine structure constant. Fractional values of the quantum number may result from existence of other form of interactions that we may not now know.
is the fine structure constant. Fractional values of the quantum number may result from existence of other form of interactions that we may not now know.
This consideration leads to the existence of a new state of hydrogen with an electron orbiting close to the proton at a distance equals to the electron classical radius. We call this electron-proton state a protonium. The physical properties of this state is similar to that of the neutron. However, the anomalous magnetic moment under this consideration is convincingly explained.
Fractional quantum numbers are observed in the quantum Hall effect (FQHE) by Tsui et al. [3], where the Hall conductance of 2D electrons shows precisely quantized plateaus at fractional values of . In this effect the electrons bind magnetic flux lines to make new quasiparticles. We argue that such a phenomenon is also reflected by hydrogen atom, when subject to external compression. In Bohr theory, an electron can’t exist at a distance less than Bohr radius.
. In this effect the electrons bind magnetic flux lines to make new quasiparticles. We argue that such a phenomenon is also reflected by hydrogen atom, when subject to external compression. In Bohr theory, an electron can’t exist at a distance less than Bohr radius.
We propose here a fractional hydrogen atom whose implication will be prominent in astrophysical objects, e.g., Neutron stars and White Dwarfs, in which gravitational compression is so immense. The electron in the atoms of these objects does not fall into the nucleus, but rather jumps into a closer stable orbits to the nucleus with  and
and , respectively. A strong magnetic field can transform a boson into a fermion or vice versa. Hence, we argue that for magnetic white dwarfs the magnetic field may alter the statistics of the white dwarf’s electrons from fermionic to bosonic. This would affect the stars structure, giving it a smaller than expected radius, and a lower than expected temperature. In some extreme cases one could imagine that this effect could lead to the collapse of the white dwarf into a neutron star.
, respectively. A strong magnetic field can transform a boson into a fermion or vice versa. Hence, we argue that for magnetic white dwarfs the magnetic field may alter the statistics of the white dwarf’s electrons from fermionic to bosonic. This would affect the stars structure, giving it a smaller than expected radius, and a lower than expected temperature. In some extreme cases one could imagine that this effect could lead to the collapse of the white dwarf into a neutron star.
This hypothesis is inspired by our recent model for the neutron. In this model, the electron exists in an orbit with a principal quantum number n equals to the fine structure constant, . This state is reached when an atom is under a very large compression. Such a state yields very huge magnetic field that is of the same order of magnitude of the neutron star. Fowler [4] showed that a system of many electrons (stars) must be governed by quantum statistical physics besides quantum mechanics, since electrons are fermions. Under high pressure electrons behave as a condensed matter system. They are governed by the laws of many-body system.
. This state is reached when an atom is under a very large compression. Such a state yields very huge magnetic field that is of the same order of magnitude of the neutron star. Fowler [4] showed that a system of many electrons (stars) must be governed by quantum statistical physics besides quantum mechanics, since electrons are fermions. Under high pressure electrons behave as a condensed matter system. They are governed by the laws of many-body system.
In this paper, we would like to investigate other possible fractional values of n and seek their astrophysical consequences. This paper is structured as follows: we study in Section II the implication of our hypothesis for the formation and characterization of neutron stars. The huge magnetic field observed in neutron stars is a result of the current developed by electrons forming our neutrons model. The surface area of a neutron star is directly proportional to its mass. The pressure of the star is related to the square of its magnetic field. We provide in Section III how one can obtain all white dwarfs stars by applying our hypothesis to hydrogen atom where the principal quantum number is a fraction. This gives exactly are characterizations (pressure, magnetic field, electric field and conductivity) of white dwarfs now known. We further apply our hypothesis of the maximal conductivity and found that white dwarfs as well as neutron stars are perfect conductors. We finally provide in Section IV the implications of our hypothesis to ordinary stars, like our sun. These stars systems exhibit the Hall effect observed in conductors under application of electric and magnetic fields. A table showing the relations between different quantities describing neutron stars, white dwarfs and ordinary stars is provided. These quantities are shown to be multiples of some powers of the fine structure constant, . This model can be compared with that standard model of formation of neutron stars and white dwarfs stars where Fermi-Dirac statistics is employed.
. This model can be compared with that standard model of formation of neutron stars and white dwarfs stars where Fermi-Dirac statistics is employed.
2. Neutron Star
Recall that in Bohr theory, the orbit, velocity and energy of the electron are given by
 (1)
(1)
where . We have found that when the magnetic force inside the atom is considered, a new stable orbit exists. This stable orbit is equivalent to considering a fractional quantum number,
. We have found that when the magnetic force inside the atom is considered, a new stable orbit exists. This stable orbit is equivalent to considering a fractional quantum number,  in Bohr’s model. Hence, Equation (1) yields
in Bohr’s model. Hence, Equation (1) yields
 (2)
(2)
Interestingly, the radius of this orbit is equal to the classical electron radius,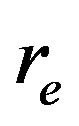 .
.
One can calculate the current resulting from the motion of the electron in this state as
 (3)
(3)
and the resulting magnetic field is that of a current loop, viz.,
 (4)
(4)
where  The magnetic field predicted by Equation (4) coincides with the magnetic field of neutron stars obtained by Wunner [5] & Leiby [6]. Hence, the magnetic field observed in neutron stars results from the magnetic field produced by the electron motion inside the hydrogen atom. The magnetic flux is defined by
The magnetic field predicted by Equation (4) coincides with the magnetic field of neutron stars obtained by Wunner [5] & Leiby [6]. Hence, the magnetic field observed in neutron stars results from the magnetic field produced by the electron motion inside the hydrogen atom. The magnetic flux is defined by

This can be compared with the quantum of magnetic flux that passes through the superconductor that is defined by . Does this mean that the neutron star is a giant superconductor? If we assume that the above magnetic flux is quantized in terms of
. Does this mean that the neutron star is a giant superconductor? If we assume that the above magnetic flux is quantized in terms of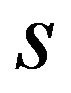 , then one can write
, then one can write , hence
, hence
 . This means the flux of the neutron star is quantized in units of
. This means the flux of the neutron star is quantized in units of , in the same way as the principal quantum numbers.
, in the same way as the principal quantum numbers.
The capacitance and inductance of the protonium are defined by
 (5)
(5)
Let us now consider the magnetic moment due to the electron in the protonium state. This is given by
 (6)
(6)
This can be compared with the measured value of the neutron and protons magnetic moments, viz.  and
and . We can get the exact value by making some linear combinations of Equation (6) and
. We can get the exact value by making some linear combinations of Equation (6) and  Using Equations (4) and (6), the Zeeman energy due to the presence of the magnetic field
Using Equations (4) and (6), the Zeeman energy due to the presence of the magnetic field  can be written as
can be written as

It is interesting that this Zeeman energy is equal to the orbital energy of the protonium. Hence, the total energy of the system is zero. Therefore, the system is at  temperature. This is the case when a Fermi-Dirac statistic is considered to describe such a system. One can further find the electric field due to protonium state as
temperature. This is the case when a Fermi-Dirac statistic is considered to describe such a system. One can further find the electric field due to protonium state as
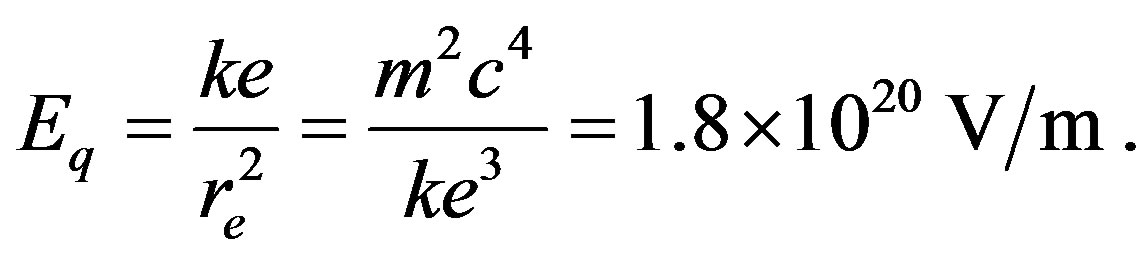 (7)
(7)
The electromagnetic energy density (or pressure) inside the protonium is
 (8)
(8)
If we consider the protonium as a dipole, we can calculate the power radiated due to Larmor dipole radiation as shown in Jackson [7]
 (9)
(9)
Stars (mainly hydrogen) are affected by their selfgravitating energy and the gas energy. At equilibrium (balance) the gravity and gas (neutron Fermi gas) pressures are equal. The gravitational pressure is defined as1
 (10)
(10)
where  is some fixed number related to the equation of state of the matter under consideration. According to Newtonian gravity, this occurs when the gas radius
is some fixed number related to the equation of state of the matter under consideration. According to Newtonian gravity, this occurs when the gas radius  is related to the star mass
is related to the star mass 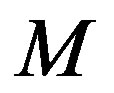 as shown by Phillips [8]
as shown by Phillips [8]
 (11)
(11)
where  Owing to Equations (10) and (11), a neutron star of mass
Owing to Equations (10) and (11), a neutron star of mass  will produce a radius of
will produce a radius of  and a pressure of
and a pressure of . In our present model, a pressure of ~1033 Pa will produce a magnetic field of
. In our present model, a pressure of ~1033 Pa will produce a magnetic field of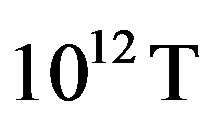 . This is also apparent from substituting Equations (4) and (8) to yield
. This is also apparent from substituting Equations (4) and (8) to yield
 (12)
(12)
Using Equations (8) and (10) the radius mass relation is
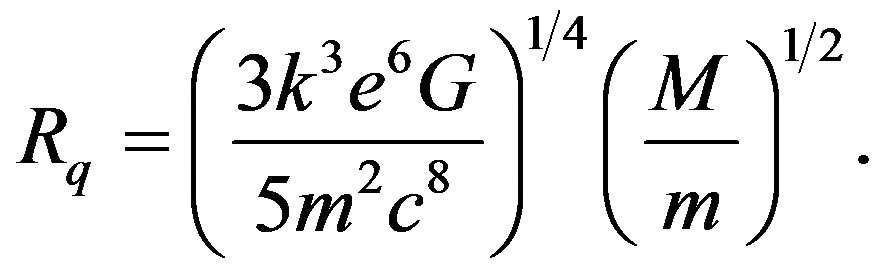 (13)
(13)
This implies that the pressure is constant. It is thus different from the standard relation, i.e.,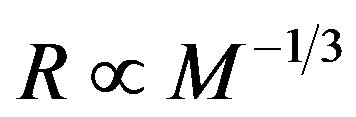 . The radius in Equation (13) can be made to give a different value if we take into consideration the relativistic mass resulting from Equation (2) that can be defined to yield the correct value of the magnetic moment of the neutron defined in Equation (6). To resolve this, the mass of the electron should be replaced by 7 m. This replacement changes the pressure (energy density) in Equation (8) to
. The radius in Equation (13) can be made to give a different value if we take into consideration the relativistic mass resulting from Equation (2) that can be defined to yield the correct value of the magnetic moment of the neutron defined in Equation (6). To resolve this, the mass of the electron should be replaced by 7 m. This replacement changes the pressure (energy density) in Equation (8) to , and the magnetic field in Equation (4) to
, and the magnetic field in Equation (4) to . Equations (2), (5) and (9) will also change. Hence, the radius in Equation (13) will be reduced by 1/7.
. Equations (2), (5) and (9) will also change. Hence, the radius in Equation (13) will be reduced by 1/7.
Using Equation (1), one can estimate the internal temperature of this state using the energy . This yields a value of
. This yields a value of . However, if we consider the protonium as a black body, it will radiate at a temperature of
. However, if we consider the protonium as a black body, it will radiate at a temperature of . This is very close to
. This is very close to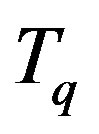 . This may permit us to assume that fermions in this state undergo a Bose-Einstein state of condensation. The energy and number densities of a Fermi-Dirac electron/ neutron gas are given by
. This may permit us to assume that fermions in this state undergo a Bose-Einstein state of condensation. The energy and number densities of a Fermi-Dirac electron/ neutron gas are given by

Let us now calculate the electrical conductivity of the protonium state as
 (14)
(14)
Using Equations (2) and (7), one obtains
 (15)
(15)
This can be set to the maximum conductively, 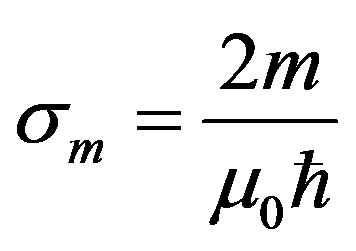 , hypothesized by Arbab [9] which yields a number density
, hypothesized by Arbab [9] which yields a number density
 (16)
(16)
This is a typical number density of nuclear matter. It is a number density of perfect conductor. Hence, neutron stars are perfect conductor. This supports the recent discovery by Page et al. [10] who have provided the first direct evidence for a superconductor state at the core of neutron stars. The current inside lasts forever as far as electrons keep circulating. The number density in Equation (16) agrees with the number density found for neutron stars by considering the Fermi statistics of the degenerate neutrons [4,11]. It is an interesting agreement. We conclude here that the above maximal conductivity hypothesis due to Arbab [9] is then verified.
Let us now calculate the impedance of the protonium state using Equation (5)
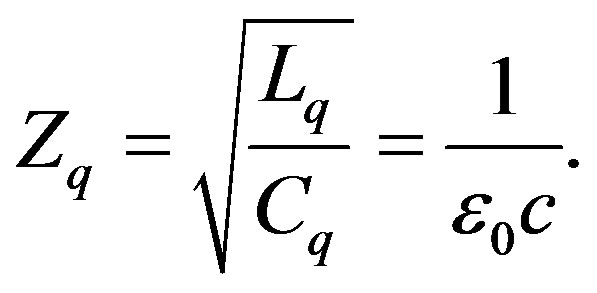 (17)
(17)
This is equal to the impedance of the vacuum. Thus, the space inside the protonium behaves as vacuum.
3. The White Dwarfs
Let us now consider the case when,
 (18)
(18)
Apply this in Equation (1) to obtain
 (19)
(19)
Such a case will lead to an interesting physical situation. It is interesting to see that the radius  in Equation (19) is equal to the Compton wavelength of the electron. We, consequently, propose that an electron under high pressure jumps to this quantum state. The physical properties of this state is described in the subsequent equations.
in Equation (19) is equal to the Compton wavelength of the electron. We, consequently, propose that an electron under high pressure jumps to this quantum state. The physical properties of this state is described in the subsequent equations.
One can also calculate the electronic current resulting from orbital motion of the electron in the quantum state described by Equation (19).
 (20)
(20)
and the resulting magnetic field is that of a current-loop, i.e.,
 (21)
(21)
It is interesting to note that the above magnetic field is a typical field of white dwarfs (~109 G) as obtained by Jordan [11,12]. The magnetic flux is defined by

The capacitance and inductance of the state in Equation (19) are defined by
 (22)
(22)
The above equation suggests that the quantum of inductance is . This implies that the neutron star has a quantum of inductance that is
. This implies that the neutron star has a quantum of inductance that is  times that of the white dwarf. One can relate this to the maximum conductivity by
times that of the white dwarf. One can relate this to the maximum conductivity by . Moreover, the quantum of resistivity is
. Moreover, the quantum of resistivity is . Hence, the quantum of resistivity is equal to
. Hence, the quantum of resistivity is equal to 
times the quantum of inductance. The quantum of conductivity represent the maximum conductivity that a system can have. Metals will have a conductivity that is equal to  times this quantum. Similarly, the quantum of capacitance is
times this quantum. Similarly, the quantum of capacitance is . These quanta are characteristic values of any quantum system.
. These quanta are characteristic values of any quantum system.
We now calculate the electric field of the state defined by Equation (4) as
 (23)
(23)
The electric energy densities are thus
 (24)
(24)
The pressure associated with this energy density amounts to .
.
Let us now consider the magnetic moment due to the electron in the above state. This is given by
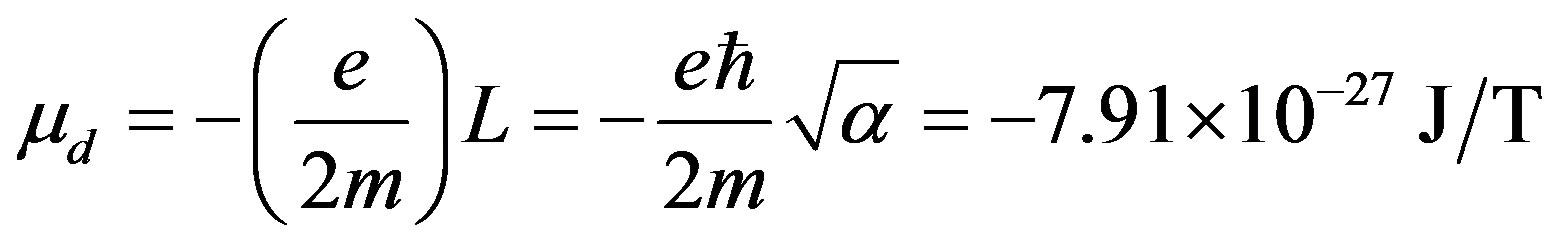 (25)
(25)
Because of the magnetic field, as in Equation (21), the Zeeman energy is given by
 (26)
(26)
If we consider the state in Equation (19) as a dipole, we can calculate the power radiated due to Larmor dipole radiation as explained in Jackson [7]
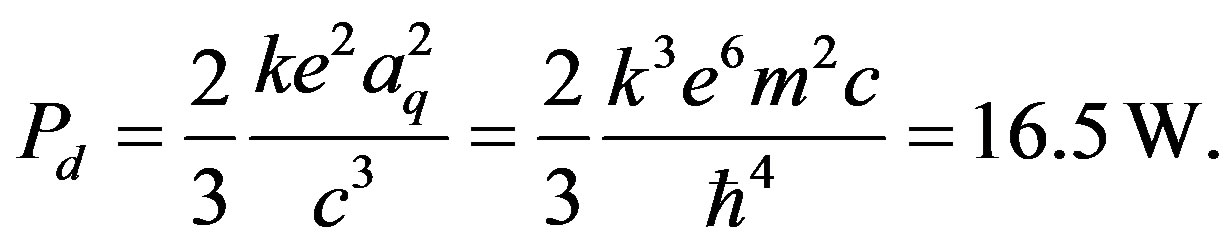 (27)
(27)
This exceedingly small power may explain the faintness of the white dwarfs.
Let us now calculate the conductivity of the state defined in Equation (14) using Equations (19) and (23) to obtain
 (28)
(28)
For a maximum conductivity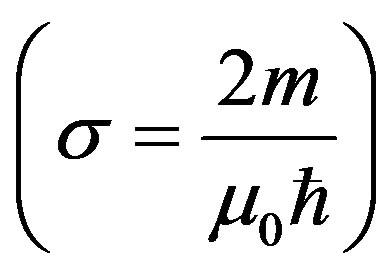 , one obtains
, one obtains
 (29)
(29)
The above value of  agrees with the number density found for white dwarfs by considering the Fermi statistics of the degenerate electrons as formulated by Fowler [4], Jordan [11] and Fassbinder [12]. Hence, white dwarfs can be thought of as perfect conductors. If we now equate the conductivity in Equations (15) and (28) to Drude conductivity of metals developed by Drude
agrees with the number density found for white dwarfs by considering the Fermi statistics of the degenerate electrons as formulated by Fowler [4], Jordan [11] and Fassbinder [12]. Hence, white dwarfs can be thought of as perfect conductors. If we now equate the conductivity in Equations (15) and (28) to Drude conductivity of metals developed by Drude
[13], 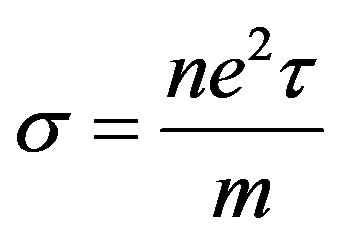 , then the relaxation time,
, then the relaxation time,  , for the neutrons in neutron star and the electrons in the white dwarfs, will be
, for the neutrons in neutron star and the electrons in the white dwarfs, will be  respectively. While
respectively. While
 and
and , electrons in metal have
, electrons in metal have  , and a number density of
, and a number density of  It is interesting to note that
It is interesting to note that 
The gravitational pressure of the white dwarfs, at equilibrium, is balanced by the electrons gas pressure. As seen from Equation (24), the gravitational energy of the white dwarfs is supported by their electrical energy. The magnetic energy of the white dwarf is negligible in comparison with the electric energy. Hence, under equilibrium one must have
 (30)
(30)
where  is the radius of the star and
is the radius of the star and  it’s mass. Therefore, the equilibrium radius
it’s mass. Therefore, the equilibrium radius 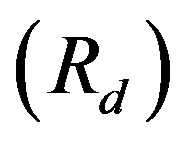 is
is
 (31)
(31)
It is interesting to that the radius mass relation we have obtained, i.e.,  , that implies the pressure is constant, is different from the standard formula, viz.,
, that implies the pressure is constant, is different from the standard formula, viz., . Despite this, we obtain similar result. Owing to Equation (31) a white dwarf of a mass
. Despite this, we obtain similar result. Owing to Equation (31) a white dwarf of a mass  will have a radius of
will have a radius of . This agrees with the observed radii of white dwarfs. This radius is close to the radius of the Earth (6378 km). Hence, we conclude that a white dwarf with mass of the Sun will have a radius of 4155 km and dominated by an electric field of
. This agrees with the observed radii of white dwarfs. This radius is close to the radius of the Earth (6378 km). Hence, we conclude that a white dwarf with mass of the Sun will have a radius of 4155 km and dominated by an electric field of  as obtained by Leiby [6] and Jordan [11]. These are typical values for the observed white dwarfs. Hence, hydrogen atom in white dwarfs are in state of a fractional quantum number,
as obtained by Leiby [6] and Jordan [11]. These are typical values for the observed white dwarfs. Hence, hydrogen atom in white dwarfs are in state of a fractional quantum number, . The electrons comprising the white dwarf are at a distance equals to the Compton wavelength of the electron in the hydrogen atom.
. The electrons comprising the white dwarf are at a distance equals to the Compton wavelength of the electron in the hydrogen atom.
One can estimate the internal temperature of the electron by equating the energy in Equation (19) to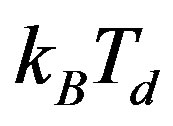 , hence one finds
, hence one finds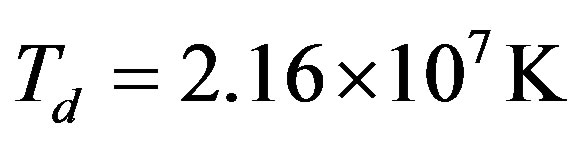 .
.
4. Ordinary Stars
An ordinary star (e.g., the Sun) is the one which is supported by hydrogen gas (with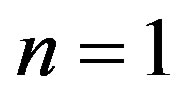 ) under gravitational compression. The ground state of hydrogen atom is defined by
) under gravitational compression. The ground state of hydrogen atom is defined by
 (32)
(32)
The electric field is given by
 (33)
(33)
This state is characterized by having an electric energy density of
 (34)
(34)
This amounts to a value of . We see from Equations (7), (23) and (33) that the electric fields of the three systems are
. We see from Equations (7), (23) and (33) that the electric fields of the three systems are
 (35)
(35)
The balance between the gravitational pressure and the internal hydrogen pressure will produce a stable star. Equating Equations (10) and (34) yields the radius of a stable star as
 (36)
(36)
The above formula can be used as a benchmark to calculate the radii of stars from their respective masses or vice versa. To reproduce the Sun’s radius,
 . Thus, Equation (36) can be written as
. Thus, Equation (36) can be written as

We remark here that the physical properties of ordinary metals are similar to ordinary stars (e.g., Sun). It is reported by Weir et al. that hydrogen becomes a metal at a pressure greater than  [14].
[14].
Using Equations (14) and (33), the conductivity in this state can be written as
 (37)
(37)
For neutron and white dwarf stars, one finds
 (38)
(38)
Equations (37) and (38) can be combined to give
 (39)
(39)
where ,
,  ,
, 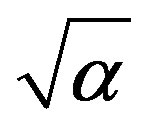 , correspond to the quantum number defining the hydrogen atom in the three states defined before (ordinary, neutron and white dwarf stars). These forms can be related to Ohm’s law for a conductor of length
, correspond to the quantum number defining the hydrogen atom in the three states defined before (ordinary, neutron and white dwarf stars). These forms can be related to Ohm’s law for a conductor of length  and cross-sectional area
and cross-sectional area , whose resistance is R, by
, whose resistance is R, by
 (40)
(40)
In FQHE the quantum of conductance is . The FQHE is thought to result from many-electron interactions in 2-dimensional systems under low temperature and strong magnetic field. Here, the FQHE may take place in these systems due to the high compression of their matter as shown by Morawicz et al. [15].
. The FQHE is thought to result from many-electron interactions in 2-dimensional systems under low temperature and strong magnetic field. Here, the FQHE may take place in these systems due to the high compression of their matter as shown by Morawicz et al. [15].
If we consider the number density in hydrogen as,
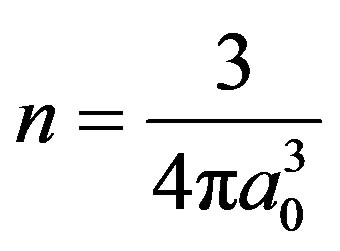 , then Equation (37) yields
, then Equation (37) yields so that
so that . One can find the relaxation time for ordinary star medium (atoms) from equating the conductivity in Equation (36) to
. One can find the relaxation time for ordinary star medium (atoms) from equating the conductivity in Equation (36) to . This yields,
. This yields, 
Using Equations (4), (14) and (15), the Hall coefficient  for a neutron is
for a neutron is
 (41)
(41)
Using Equations (14), (21) and (28), the Hall coefficient for a white dwarf star is
 (42)
(42)
Using Equations (14), (32) and (37), the Hall coefficient for an ordinary star
 (43)
(43)
Equations (41), (42) and (43) clearly show that the Hall effect exists in astrophysical systems with quantized coefficient in powers of . It is interesting to notice that the radii for ordinary, neutron and white dwarf stars can be related to each other. Therefore, using Equations (13), (31), (35) and (36), one obtains
. It is interesting to notice that the radii for ordinary, neutron and white dwarf stars can be related to each other. Therefore, using Equations (13), (31), (35) and (36), one obtains
 (44)
(44)
Owing to Equations (31) and (44), Sirius B of radius  will have a mass of 1.15Me instead of 0.978Me as obtained by Holberg et al. [16] and Liebert et al. [17]. However, Equations (31) and (44) agree with the Landsman et al. [18] findings of the hot white-dwarf companions.
will have a mass of 1.15Me instead of 0.978Me as obtained by Holberg et al. [16] and Liebert et al. [17]. However, Equations (31) and (44) agree with the Landsman et al. [18] findings of the hot white-dwarf companions.
We provide in Table 1 the relation between different quantities describing neutron stars, white dwarfs and ordinary stars.
5. Conclusion
We have proposed in this paper that fractional quantum numbers exist in hydrogen atom. These are powers of the fine structure constant. The first number gives rise to the physical properties of the neutron star, and the second one to the white dwarf stars. These fractional quantum numbers were first shown to exist in quantum Hall effect. We propose a quantum of inductance and capacitance in addition to the quantum of flux and conductance. We have shown in this paper that neutron and white dwarf star got the maximum possible conductivity in nature. Hence, these stars are examples of giant perfect conductors at a relatively high temperature and magnetic field.

Table 1. A comparison between neutron, white dwarf and ordinary stars physical properties.
Moreover, these systems exhibit a fractional quantum effect. The Hall coefficient of these systems are quantized in terms of . The radii of these systems are also intimately connected. It is important to point out that the other set of fractional values of n led to un physical situation.
. The radii of these systems are also intimately connected. It is important to point out that the other set of fractional values of n led to un physical situation.
NOTES