Fixed Point and Common Fixed Point Theorems for Cyclic Quasi-Contractions in Metric and Ultrametric Spaces ()
1. Introduction
Since Banach [1] proved his contraction principle in 1922, many authors have improved, extended and generalized Banach’s contraction principle in several ways and applied the principle to differential and integral equations, variational inequality theory, complementarity problems, equilibrium problems, optimization problems, convex analysis and many others.
Theorem 1.1 [1] Let  be a self-mapping on a complete metric space
be a self-mapping on a complete metric space . If there exists
. If there exists  such that
such that

for all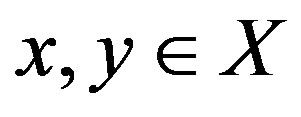 , then f has a unique fixed point in X.
, then f has a unique fixed point in X.
In 1971, Ććirić [2] generalized Banach’s contraction principle theorem to a more general contraction as follows:
Theorem 1.2 [2] Let  be a complete metric space and
be a complete metric space and 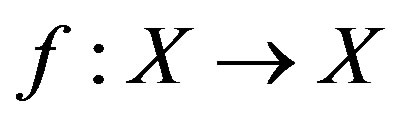 be a mapping such that, for all
be a mapping such that, for all , there exists
, there exists  with
with  such that
such that

Then f has a unique fixed point.
Also, in 1974, Ććirić [3] generalized his own result [2] by introducing the quasi-contraction and proved a fixed point theorem under this condition as follows:
Definition 1.3 [3] A mapping  of a metric space
of a metric space  into itself is said to be a quasi-contraction if there exists a number
into itself is said to be a quasi-contraction if there exists a number  such that
such that

for all .
.
Theorem 1.4. [3] Let  be a complete metric space and
be a complete metric space and  be a quasi-contraction. Then f has a unique fixed point in X.
be a quasi-contraction. Then f has a unique fixed point in X.
In 2005, Rus [4] introduced the cyclical condition in metric spaces. For some results on fixed point theory, we refer the readers to [5-7]. Throughout this paper, we denote the set  by
by .
.
Definition 1.5. [4] Let  be a nonempty set and
be a nonempty set and
 be a mapping. The set
be a mapping. The set  is called a cyclic representation of X with respect to f if the following conditions hold:
is called a cyclic representation of X with respect to f if the following conditions hold:
1) ;
;
2)  is a nonempty subset of
is a nonempty subset of 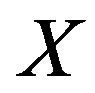 for all
for all ;
;
3)  for all
for all .
.
Definition 1.6. Let ,
,  ,
,  and
and . Now, we define a selfmapping f on X by
. Now, we define a selfmapping f on X by

Now, we see that ,
,  and
and  . Therefore, the set
. Therefore, the set  is a cyclic representation of X with respect to f.
is a cyclic representation of X with respect to f.
Definition 1.7. Let X be a nonempty set, 
be a mapping and the set  be a cyclic representation of X with respect to f. If
be a cyclic representation of X with respect to f. If  and
and  for some
for some , we say that x1 and x2 are descendants in Y.
, we say that x1 and x2 are descendants in Y.
The purpose of this paper is to extend Ććirić’s quasicontraction to a cyclic quasi-contraction, establish some fixed point theorems and give an example to illustrate the main result. We also introduce the notion of co-cyclic quasi-contraction and prove some common fixed point theorems.
2. Fixed Point Theorems
In this section, we introduce a generalization of Ććirić’s quasi-contraction, say, a cyclic quasi-contraction, and prove some fixed point theorems.
Definition 2.1. Let  be nonempty closed subsets of a metric space
be nonempty closed subsets of a metric space ,
,  and
and
 be a mapping. If the following conditions are satisfied:
be a mapping. If the following conditions are satisfied:
1) 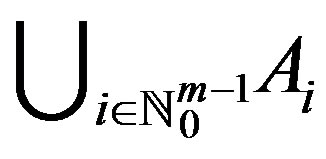 is a cyclic representation of Y with respect to f;
is a cyclic representation of Y with respect to f;
2) there exists  such that
such that

whenever  and
and  are descendants in
are descendants in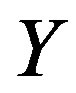 , then
, then  is called a cyclic quasi-contraction.
is called a cyclic quasi-contraction.
Remark 2.2. To reduce a cyclic quasi-contraction to a quasi-contraction, simply take each  and the result directly emerges.
and the result directly emerges.
Now, we can construct some fixed point theorems, which generalize the further results, as follows:
Theorem 2.3. Let  be nonempty closed subsets of a complete metric space
be nonempty closed subsets of a complete metric space  and
and
 . Suppose that
. Suppose that  is a cyclic quasi-contraction with
is a cyclic quasi-contraction with . Then f has a unique fixed point
. Then f has a unique fixed point  and the sequence
and the sequence 
converges to  for any
for any 
Notice that the  -constant in the quasi-contraction is restricted to the set
-constant in the quasi-contraction is restricted to the set . Next, we can drop this restriction and develop a theorem in an ultrametric space. The result follows from the additional assumption of an ultrametric space. Before we give the result, we now give the definition of an ultrametric space.
. Next, we can drop this restriction and develop a theorem in an ultrametric space. The result follows from the additional assumption of an ultrametric space. Before we give the result, we now give the definition of an ultrametric space.
Definition 2.4. Let  be a nonempty set. A function
be a nonempty set. A function  is called an ultrametric if it satisfies the following conditions:
is called an ultrametric if it satisfies the following conditions:
1)  and
and  if and only if x = y for all
if and only if x = y for all ;
;
2)  for all
for all ;
;
3)  for all
for all  .
.
A set X equipped with this ultrametric , denoted
, denoted , is called an ultrametric space.
, is called an ultrametric space.
Remark 2.5. Note that an ultrametric space is also a metric space. We can simply prove this. In fact, for any ,
,

which in turn is a metric.
Theorem 2.6. Let  be nonempty closed subsets of a complete ultrametric space
be nonempty closed subsets of a complete ultrametric space  and
and
 . Suppose that
. Suppose that  is a cyclic quasi-contraction. Then
is a cyclic quasi-contraction. Then  has a unique fixed point
has a unique fixed point  and the sequence
and the sequence  converges to
converges to  for any
for any .
.
Now, we prove Theorem 2.3. The proof of Theorem 2.6 is quite similar to the proof of Theorem 2.3, we omit to prove this theorem.
Proof of Theorem 2.3. Let 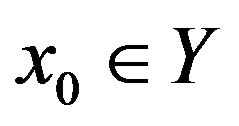 be arbitrarily chosen. Define a sequence
be arbitrarily chosen. Define a sequence  by
by 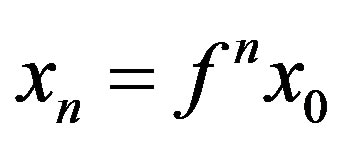 for all
for all . If there exists a positive integer n0 such that
. If there exists a positive integer n0 such that , the the proof is finished. So, assume that
, the the proof is finished. So, assume that
 for all
for all . Since
. Since , there exists
, there exists
 such that
such that . Therefore,
. Therefore,  and, by induction, we have
and, by induction, we have . Hence we have
. Hence we have
 (1)
(1)
Assume that

Then we can see that , which is a contradiction. Therefore, from (1), it follows that
, which is a contradiction. Therefore, from (1), it follows that

Consequently, we can deduce that
 , where
, where . By repeating this process, we have
. By repeating this process, we have .
.
Thus it is easily seen that  is a Cauchy sequence in Y. Since Y is closed in X, Y is a complete subspace of X and so
is a Cauchy sequence in Y. Since Y is closed in X, Y is a complete subspace of X and so  converges to some point
converges to some point . Denote
. Denote . Now, we show that
. Now, we show that . Sincefor each
. Sincefor each , we have
, we have , it is easy to see that, for each
, it is easy to see that, for each , Ai contains infinitely many points of
, Ai contains infinitely many points of . Since Ai is closed for each
. Since Ai is closed for each , we can construct a subsequence of
, we can construct a subsequence of  in Ai which converges to
in Ai which converges to . Therefore,
. Therefore, . In other words, Z is nonempty.
. In other words, Z is nonempty.
Consider the restriction  of the function
of the function . We can see that it maps
. We can see that it maps  into itself, i.e.,
into itself, i.e., . Then it is easily proved, by applying Theorem 1.4, that
. Then it is easily proved, by applying Theorem 1.4, that  has a unique fixed point
has a unique fixed point . Thus
. Thus  is also a fixed point of
is also a fixed point of .
.
Now, assume that there exists another fixed point of  denoted by
denoted by . Since
. Since , we have
, we have 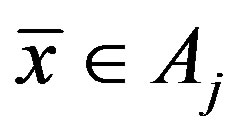 for some
for some . Therefore,
. Therefore,  and
and  are descendants in
are descendants in . Hence we have
. Hence we have

which implies that , that is,
, that is,  is the unique fixed point of
is the unique fixed point of .
.
Next, we show that . Since Z and
. Since Z and  , we have
, we have
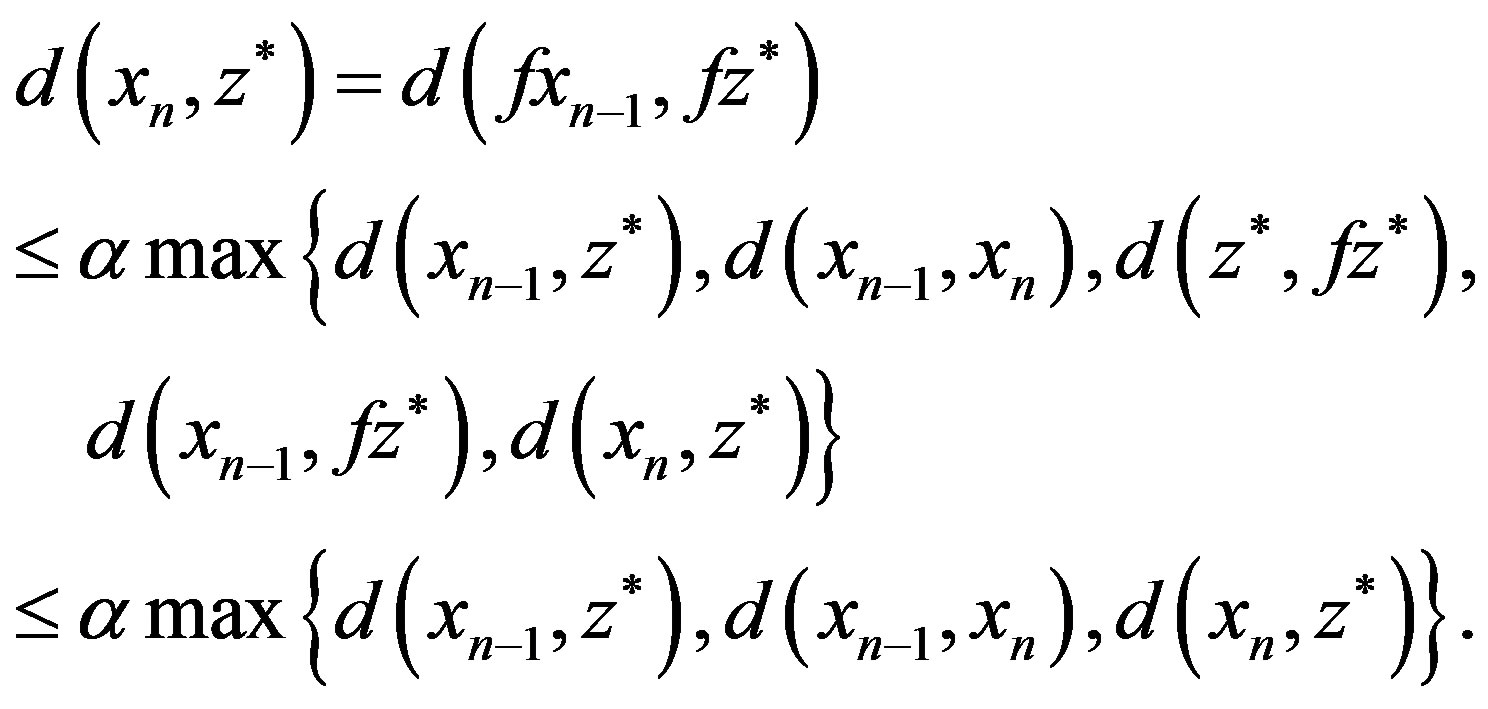 (2)
(2)
We have a contradiction if

So, we claim that

Hence, from (2), it follows that

Thus, by repeating this process, we obtain
 . Therefore, we have
. Therefore, we have , that is,
, that is,  converges to the unique fixed point
converges to the unique fixed point  of
of  in
in  for any initial
for any initial . This complete the proof. ■
. This complete the proof. ■
Proof of Theorem 2.6. Let  be arbitrary. Define a sequence
be arbitrary. Define a sequence  as in the proof of Theorem 2.3. Following the proof lines, we obtain
as in the proof of Theorem 2.3. Following the proof lines, we obtain

By repeating this process, we get
 . Then it is easily seen that the sequence
. Then it is easily seen that the sequence  is a Cauchy sequence and so, from the completeness of
is a Cauchy sequence and so, from the completeness of ,
,  converges to some point
converges to some point
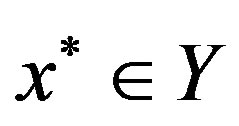 . We can show, by using the proof of Theorem 2.3, that
. We can show, by using the proof of Theorem 2.3, that  is not empty. More precisely,
is not empty. More precisely,  .
.
Now, we consider the restriction  of the function
of the function . Note that the strong triangle inequality also implies the ordinary triangle inequality. Hence Theorem 1.4 can be applied to confirm the existence of a unique fixed point
. Note that the strong triangle inequality also implies the ordinary triangle inequality. Hence Theorem 1.4 can be applied to confirm the existence of a unique fixed point  of
of  in
in . By the proof of Theorem 2.3, we can show that
. By the proof of Theorem 2.3, we can show that  is also the unique fixed point of
is also the unique fixed point of .
.
Now, we show that the sequence  converges to z* for any
converges to z* for any . Since
. Since  and
and , we have
, we have


We can see that
 .
.
Otherwise, we have a contradiction. Hence we have

Again, by repeating this procedure, we obtain
 . Then the sequence
. Then the sequence  converges to the unique fixed point
converges to the unique fixed point  of
of  in
in  for any initial
for any initial . This completes the proof. ■
. This completes the proof. ■
Notice that our results do not only generalize Ććirić’s result, but also make it easier to determine the fixed point of a given mapping as in the following example:
Example 2.7. Consider a weighted graph
 whose
whose  makes G a complete K4 graph with weights
makes G a complete K4 graph with weights  for each
for each 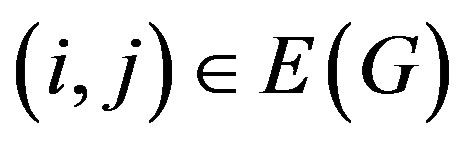 given as follows:
given as follows:

For the understanding of the readers, we illustrate G as a figure in the following:

Now, define a function  by letting, for all
by letting, for all ,
,  if i = j and
if i = j and  if
if  (we can do this because the graph G is complete). By this setting, it is easy to verify that
(we can do this because the graph G is complete). By this setting, it is easy to verify that  is a complete metric space. Set
is a complete metric space. Set  and
and , we have A0 and A1 being two closed subsets of
, we have A0 and A1 being two closed subsets of . Suppose that the mapping
. Suppose that the mapping  given by the following:
given by the following:

By a careful calculation, we may obtain that  is a cyclic quasi-contraction on
is a cyclic quasi-contraction on . Thus,
. Thus,  has a unique fixed point
has a unique fixed point  and
and  for every
for every .
.
3. Common Fixed Point Theorems
In this section, we prove some common fixed points theorems for the co-cyclic conditions. Before we can prove our results, we also need the following, which is an extension of Definition 2.
Definition 3.1. Let X be a nonempty set and
 be two mappings. The set
be two mappings. The set  is called a co-cyclic representation of X between f and g if the following conditions are satisfied:
is called a co-cyclic representation of X between f and g if the following conditions are satisfied:
1) ;
;
2)  is a non-empty subset of
is a non-empty subset of  for all
for all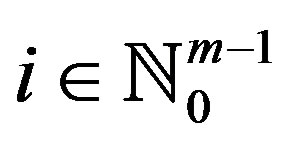 ;
;
3)  for all
for all .
.
Example 3.2. Let ,
,  ,
, 
and . Now, define two self-mappings f, g on X by
. Now, define two self-mappings f, g on X by


Now, we see that
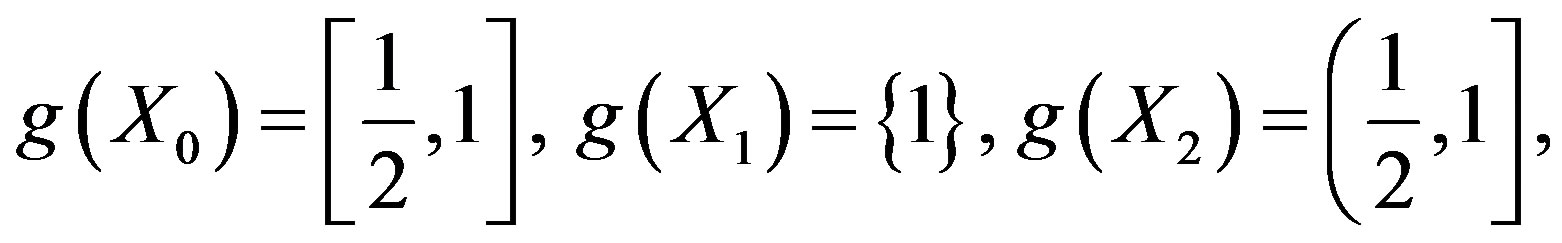

Therefore,  ,
,  and
and
 . That is,
. That is,  is a co-cyclic representation of X between f and g.
is a co-cyclic representation of X between f and g.
Definition 3.3. Let  be nonempty closed subsets of a metric space
be nonempty closed subsets of a metric space ,
,  and
and
 be two mappings. If the following conditions are satisfied:
be two mappings. If the following conditions are satisfied:
1)  is a co-cyclic representation of Y between f and g;
is a co-cyclic representation of Y between f and g;
2) there exists  such that
such that

whenever x and y are descendants in Y, then we say that f and g are  -co-cyclic quasi-contraction.
-co-cyclic quasi-contraction.
Remark 3.4. The notions and results in this section can be reduced from the results of the previous section if the mapping g is the identity mapping.
Now, we are ready to give some extensions of the results in Section 2.
Theorem 3.5. Let  be nonempty closed subsets of a complete metric space
be nonempty closed subsets of a complete metric space  and
and
 . Suppose that
. Suppose that  are
are  - co-cyclic quasi-contraction with
- co-cyclic quasi-contraction with ,
,  is a mapping and
is a mapping and  is closed for all
is closed for all
 . Then f and g have a unique point of coincidence in
. Then f and g have a unique point of coincidence in .
.
Theorem 3.5 can be proved using the analogous ideas of the proofs in Section 2. However, we prove Theorem 3.5 differently by using the following lemma ([8]):
Lemma 3.6. [8] Let  be a nonempty set and
be a nonempty set and  be a mapping. Then there exists a subset
be a mapping. Then there exists a subset  such that
such that  and
and 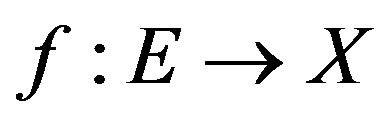 is an injection.
is an injection.
Proof of Theorem 3.5. By Lemma 3.2, for each , there exists
, there exists  such that
such that 
 and
and  is an injection. Define
is an injection. Define
 and a mapping
and a mapping  by hgx = fx. It is easy to see that
by hgx = fx. It is easy to see that

for each , which further implies that
, which further implies that 
is a cyclic representation of W with respect to h. Moreover, we can write the  -co-cyclic quasi-contraction with
-co-cyclic quasi-contraction with  in terms of a cyclic quasi-contraction as follow:
in terms of a cyclic quasi-contraction as follow:

Since W is complete, by using Theorem 2.3, we show that there exists a unique fixed point  of h in
of h in
 . In fact, this means
. In fact, this means .
.
Furthermore, we can see that w is also the unique point of coincidence of f and g in . This completes the proof.
. This completes the proof.
Note that our conditions are not strong enough to show the existence of a common fixed point of two mappings. To guarantee the existence and uniqueness of a common fixed point, we need an additional condition, namely, a weak compatibility, which is defined as follows:
Definition 3.7. [9] Let X be a nonempty set. Two mappings  are said to be weakly compatible if they commute at their point of coincidences, i.e., if
are said to be weakly compatible if they commute at their point of coincidences, i.e., if  is such that
is such that , then
, then .
.
Theorem 3.8. Suppose that all the conditions in Theorem 3.5 hold. If f and g are weakly compatible, then f and g have a unique common fixed point.
Proof. Since all the conditions in Theorem 3.5 hold, it follows that f and g have a unique point of coincidence w of f and g, that is,  in
in . If f and g are weakly compatible, we have
. If f and g are weakly compatible, we have
 . This means
. This means  is also a point of coincidence of f and g. Since the point of coincidence of f and g is unique, we have that
is also a point of coincidence of f and g. Since the point of coincidence of f and g is unique, we have that , that is, w is a common fixed point between f and g.
, that is, w is a common fixed point between f and g.
For the uniqueness of the point w, suppose that . Hence z is a point of coincidence of f and g. Since the point of coincidence of f and g is unique, we conclude that
. Hence z is a point of coincidence of f and g. Since the point of coincidence of f and g is unique, we conclude that . Thus f and g have a unique common fixed point w in Z. This completes the proof.
. Thus f and g have a unique common fixed point w in Z. This completes the proof.
Theorem 3.9. Let  be nonempty closed subsets of a complete ultrametric space
be nonempty closed subsets of a complete ultrametric space  and
and
 . Suppose that
. Suppose that  are
are 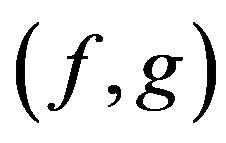 - co-cyclic quasi-contraction,
- co-cyclic quasi-contraction,  is a mapping and
is a mapping and  is closed for all
is closed for all . Then f and g have a unique point of coincidence in
. Then f and g have a unique point of coincidence in . Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.
. Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.
The proof of this theorem can be completed using the proof of Theorems 2.6, 3.5 and 3.8 and so we omit here.
Corollary 3.10. Let  be nonempty closed subsets of a complete metric space
be nonempty closed subsets of a complete metric space  and
and
 . Let f and g be two self-mappings on Y.
. Let f and g be two self-mappings on Y.
Suppose that there exist  such that
such that
 (3)
(3)
whenever x and y are descendants in Y, where
 ,
,  is a mapping and
is a mapping and  is closed for all
is closed for all . Suppose that
. Suppose that  is a co-cyclic representation of Y between f and g. Then f and g have a unique point of coincidence in
is a co-cyclic representation of Y between f and g. Then f and g have a unique point of coincidence in .
.
Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.
Proof. Since f and g satisfy the inequality (3), we can deduce that

Now, since , applying Theorems 3.5 and 3.8, we obtain the result.
, applying Theorems 3.5 and 3.8, we obtain the result.
Corollary 3.11. Let  be nonempty closed subsets of a complete ultrametric space
be nonempty closed subsets of a complete ultrametric space 
and . Let f and g be two self-mappings on Y. Suppose that there exist
. Let f and g be two self-mappings on Y. Suppose that there exist
 such that
such that

whenever x and y are descendants in Y, where
 ,
,  and
and  is closed for all
is closed for all . Suppose that
. Suppose that  is a co-cyclic representation of Y between f and g. Then f and g have a unique point of coincidence in
is a co-cyclic representation of Y between f and g. Then f and g have a unique point of coincidence in . Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.
. Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.
Proof. Since f and g satisfy the inequality (3), it follows that
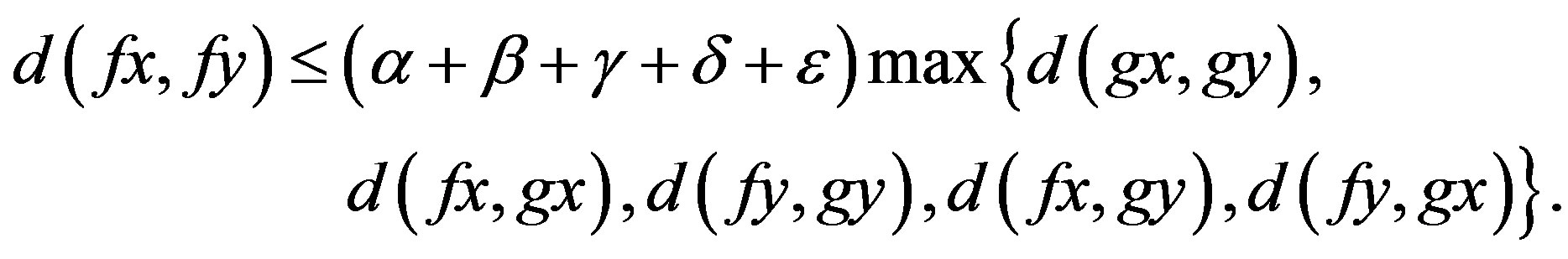
Now, since , applying Theorem 3.4, we obtain the result.
, applying Theorem 3.4, we obtain the result.
If g is the identity mapping in Corollaries 3.5 and 3.6, we have the following:
Corollary 3.12. Let  be nonempty closed subsets of a complete metric space
be nonempty closed subsets of a complete metric space  and
and
 . Let f be a self-mapping on Y. Suppose that there exist
. Let f be a self-mapping on Y. Suppose that there exist  such that
such that

whenever x and y are descendants in Y, where
 . Suppose that
. Suppose that  is a cyclic representation of Y with respect to f. Then f has a unique fixed point in
is a cyclic representation of Y with respect to f. Then f has a unique fixed point in .
.
Corollary 3.13. Let  be nonempty closed subsets of a complete ultrametric space
be nonempty closed subsets of a complete ultrametric space  and
and
 . Let f be a self-mapping on Y. Suppose that there exist
. Let f be a self-mapping on Y. Suppose that there exist  such that
such that

whenever x and y are descendants in Y, where
 . Suppose that
. Suppose that  is a cyclic representation of Y with respect to f. Then f has a unique fixed point in
is a cyclic representation of Y with respect to f. Then f has a unique fixed point in .
.
Remark 3.14. Notice that Corollary 3.12 also generalizes the condition  of Theorem 1.2.
of Theorem 1.2.
4. Conclusion
For the single-mapping case, the existence and uniqueness of a fixed points for a quasi-contraction in cyclic sense is proved with a restriction that the contraction constant have to be less than . We further showed that if X is an ultrametric space, such a restriction may be dropped. Further, with the notion of a co-cyclic representation, we point out that the two-mapping case may be extended from our results proved earlier.
. We further showed that if X is an ultrametric space, such a restriction may be dropped. Further, with the notion of a co-cyclic representation, we point out that the two-mapping case may be extended from our results proved earlier.
5. Acknowledgements
The authors were supported by the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission (NRU-CSEC No.55000613). The second author was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (Grant no. 2011-0021821). The Third author would like to thank the Research Professional Development Project Under the Science Achievement Scholarship of Thailand (SAST).
NOTES