1. Introduction
Wireless networks, till date, are regulated by fixed spectrum allocation policies to operate in a particular time frame, certain frequency bands and are also constrained to geographical regions. Recent trends show that certain radio bands are overcrowded while some are moderately or sparsely used. In order to utilize the spectrum optimally and efficiently, cognitive radio technology has been proposed as a potential communication paradigm [1]. Cognitive radios are defined by the Federal Communications Commission (FCC) [2] as radio systems that continuously perform spectrum sensing, dynamically identify unused spectrum, and then operate in those spectral holes where the licensed (primary) radio systems are idle. In CR networks secondary users are allowed to utilize unoccupied bandwidths provided they do not cause interference to primary users. Many have worked on the sensing of a wideband spectrum. The main functions of cognitive radios are [3]:
Spectrum Sensing: refers to detect the unused spectrum and sharing it without any interference with other users, by sensing spectrum holes. Spectrum sensing techniques can be classified into three categories, namely 1) Transmitter detection by inspecting the spectrum generated, 2) Cooperative detection, which pools information from multiple cognitive radio users and, 3) Interference based detection, by using an interference temperature model.
Spectrum Management: Having known the spectral holes, it has to decide on the best spectrum band to meet the Quality of Service requirements over all available spectrum bands Spectrum Mobility: As the objective is to use the spectrum in a dynamic manner they should enable transition to better spectrum by secondary users.
Spectrum Sharing: Involves spectrum scheduling for efficient spectrum usage.
In this paper transmitter detection method is used. Some authors used wideband spectrum joint detection for the presence of a primary user [4]. Some have used spatial diversity to find the presence of a primary user by sharing the information over a network [5].Cognitive Radio is essential locally reuse unused spectrum by primary users (spectral holes) in order to increase the total channel capacity. Efficient spectrum utilization can be achieved by making a secondary user to access a spectrum hole created by the primary user at any location and time. The greatest task in sensing spectrum is in developing techniques which are able to detect even very weak primary user signals at the same time reasonably fast and low computational cost. This can be encountered by utilizing a novel technique called Hilbert Huang Transform [6].
2. System Model
2.1 Hilbert Huang Transform
Traditional data analysis methods are based on assumptions that the data is linear and stationary. In recent years new methods in the field of data analysis have been introduced. For example, wavelet analysis [7] and WagnerVille distribution [8,9] were designed for linear but nonstationary data. Additionally, various nonlinear time series analysis methods [10-12] were designed for nonlinear but stationary and deterministic systems. Unfortunately, in most real systems, natural or man-made, the data is most likely nonlinear and non-stationary. Analyzing the data of such a system is very difficult because the most sophisticated basis function cannot be relied as a basis function. Thus an adaptive basis function should be data defined. The Hilbert Huang Transform [6,13-15] seems to meet few of the above faced challenges.
The Hilbert Huang Transform is an empirically based data analysis method. Its basis of expansion is adaptive so that physical meaning can be derived from the nonlinear and non-stationary processes. The Hilbert Huang Transform consists of two parts: empirical mode decomposition (EMD) and Hilbert spectral analysis (HSA). We have incorporated a variant of the EMD called Empirical Ensemble Mode Decomposition (EEMD) to deal with input signals that are contaminated with noise.
2.2 Empirical Mode Decomposition
The empirical mode decomposition method is vital to deal with data from non-stationary and nonlinear process. The decomposition is based on the assumption that any data consists of different simple intrinsic modes of oscillations. Each intrinsic mode, linear or nonlinear, represents a simple oscillation, which will have the same number of extrema and zero-crossings. Furthermore, the oscillation will also be symmetric with respect to the “local mean.” At any given time, the data may have many different coexisting modes of oscillation, one superimposing on the others. The result is the final complicated data. Each of these oscillatory modes is represented by an intrinsic mode function (IMF) with the following definition:
1) In the whole dataset, the number of extrema and the number of zero-crossings must either equal or differ at most by one, and
2) At any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero.
An IMF represents a simple oscillatory mode as a counterpart to the simple harmonic function, but it is much more general: instead of constant amplitude and frequency, as in a simple harmonic component, the IMF can have a variable amplitude and frequency as functions of time.
IMFs can be generated by following the steps:
1) Identify all the local maxima and join these points using a cubic spline to give an upper envelope 2) Repeat the above procedure for local minima’s to give lower envelope. (Figure 1)
3) The mean of the envelopes is designated as m1.
4) The difference between the data and mean is the first component h1.
h1 is treated as a proto-IMF. In the next step h1 is treated as the input data and this procedure continues until the new component satisfies the IMF definition. The input data is then sifted and decomposed and the procedure continues until we obtain a monotonic residue.
2.3 Ensemble Empirical Mode Decomposition
To overcome some of the shortcomings of EMD, noise assisted data analysis method (NADA) EEMD was incorporated [6]. EMD cannot deal with signals contaminated with white noise efficiently. Due to the presence of noise a consequence of signal intermittency occurs which is termed as Mode mixing. This consequence causes serious aliasing in time-frequency distribution and also makes the physical meaning of IMF unclear. The critical concept advanced here is based on the following observations:
1) A collection of white noise cancels each other out in a time-space ensemble mean; therefore, only the signal can survive and persist in the final noise-added signal ensemble mean.
2) Finite, not infinitesimal, amplitude white noise is necessary to force the ensemble to exhaust all possible solutions; the finite magnitude noise makes the different scale signals reside in the corresponding IMF, dictated by the dyadic filter banks, and render the resulting ensemble mean more meaningful.
2.4 Hilbert Spectral Analysis
After obtaining the IMF (Figure 2) components, Hilbert Transform is applied to each IMF component. This transform gives the amplitude and the frequency of the IMF components as functions of time. The frequency-time distribution of the amplitude is termed as “Hilbert amplitude spectrum” or simply “Hilbert spectrum” (Figure 3). Squaring the amplitude gives the energy spectrum (Figure 4) which is quite useful in determining the dominant signal among a series of signals.
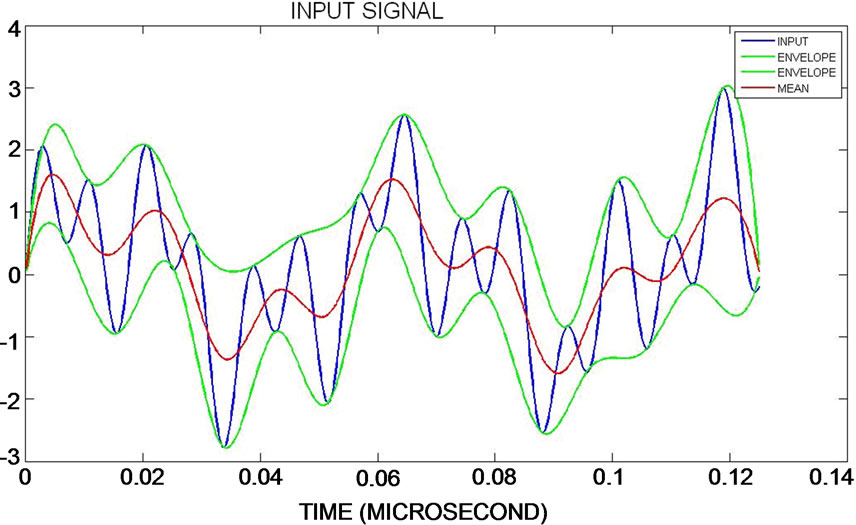
Figure 1. The data (blue) and the envelopes (green) defined by the local maxima and minima respectively. The mean (red) of then upper and lower envelope
The combination of the ensemble empirical mode decomposition and the Hilbert spectral analysis is also known as the “Hilbert–Huang transform” (HHT) for short. Empirically, all tests indicate that Hilbert Huang transform is a superior tool for time-frequency analysis of nonlinear and non-stationary data. It is based on an adaptive basis, and the frequency is defined through the Hilbert transform. Consequently, there is no need for the spurious harmonics to represent nonlinear waveform deformations as in any of the a priori basis methods, and there is no uncertainty principle limitation on time or frequency resolution from the convolution pairs based also on a priori basis.
Table 1 [6] shows that the Hilbert Huang transform is indeed a powerful method for analyzing data from nonlinear and non-stationary processes: it is based on an adaptive basis; the frequency is derived by differentiation rather than convolution; therefore, it is not limited by the uncertainty principle; it is applicable to nonlinear and non-stationary data and presents the results in time-frequency-energy space for feature extraction.