1. Introduction
At present, the explored reserves of a whole number of mineral resources are being exhausted at the readily accessible shallow deposits in safe seismic regions in Russia. Therefore, construction of new deep open pits and deepening of existing ones under complicated geological-and-mining, including seismic-dangerous, conditions is a high-priority task in Zabaykalie, Tyva, the Far East, Sakhalin, etc. In addition, at many mining regions with enormous amounts of excavated materials (e.g. Kuzbass, the Kola Peninsular, many zones of the Urals) one can observe the growth of technogeneous seismicity, that leads to enhance the influence of seismic waves on open-pit slope stability. Figure 1 shows the basic coal open-pits located within the zone of seismoactive zones of Russia. At present, most of them are positioned at Kuzbass within the zones of vibration level VI-VII, but, however, as exploring for mineral resources in Siberia and the Far East, it is expected the rise of number of opencasts being located within the zones of the intensity VIII and even IX of seismic vibrations.
The most widespread method of seismic impact accounting on stability of open pit edges and open pit slopes is pseudo static approach [2-10]. However application of it leads to sufficient strong overstating of safety factor and ignores existing information about influence of relative small but longstanding oscillations from far earthquakes on the slopes stability, for instance [11].
Alternative method of accounting of earthquake vibration influence involves transfer of evaluation methods of seismic-explosive waves influence on the influence of seismic waves [12-15]. At that it is suggested to enter additional coefficients for accounting essential major endurance and predominate period and all oscillation process [15].
In the foreign practice beside of pseudo static approach [16-19], numerical dynamic calculations are used for evaluation of stability of natural slopes, embankments, dams and open pit edges at earthquakes by using different software packages (Abacus, Plaxis, ANSYS, Slope/W, Flack, UDEC, 3DEC) and Newmark’s deformational method [20-27].
For the numerical dynamic calculations are necessary detailed knowledge of structure and properties of slope including dynamic characteristics describing the wave’s propagation and dynamic strength, and also rheological properties reflecting the behavior of failing rock mass after short-term local excesses of dynamic ultimate strength. Actually, that makes rather problematic the real estimation of influence of earthquakes on open-pit slopes with the use of numerical methods.
Complexities appear that consist of a variety of factors when using Newmark’s deformational method. Firstly, in zones having no long-term history of seismic monitoring of heavy earthquakes, this method is more suitable for analysis of situations after earthquake, but not for forecasting or designing, because it is required either a real accelerogram or a synthetic accelerogram based on statistical treatment of the earthquake records near to the existing or designed open-pit mine. Secondly, this method does not realize a lot of significant factors, examined in the Newmark’s article, including the influence of the wave’s spectrum, potential irreversible movements, etc. Thirdly, Newmark’s approaches themselves do not account many important factors [28-30], first of all, the processes for displacement development, differences between sliding friction and friction at rest, dynamic strength and deformation characteristics and static ones, etc.
2. Methodology of Experiments
In this connection a decision was made to use the method of physical modeling. The problem in physical modeling was in that the effects of strong seismic waves on openpit slope represent a simultaneous follow of slow (quasistatic) and dynamic processes, and each of them is of important significance. Therefore, in modeling with use of equivalent materials it was necessary to provide the similarity both of those and other processes.
Traditionally in physical modeling of open-pit slopes great models from rather weak and plastic equivalent materials were used, which may be deformed under their own weight [31]. This method, however, for modeling of seismic effects on open-pit slopes is not suitable due to a number of reasons: the use of mechanical ties highly affects the wave’s propagation; difficulty in creation of uniform dynamic load in the model of great dimensions; limitation of amount of tests preventing the statistical reliability of the results. In investigation of dynamic processes one can not ignore the wavy phenomena. Therefore, in modeling, first of all, it is necessary to ensure the similarity of deformation characteristics of rock mass.
Investigations of deformation characteristics of equivalent materials under dynamic and static loading conditions were carried out on models from sand-epoxyaliphatic materials (SEM) with various percentage of bonding: 0.9%, 1.2%, 11% and 15%. With using standard methods the speed of elastic longitudinal and lateral waves was determined, as well as dynamic and static module of elasticity, strength in uniaxial compression. Tests have shown that in direct ultrasonic measurements of specimens from equivalent materials one observed high velocity of wave propagation, and difference between the dynamic and static module of elasticity amounted to 6 - 8 and even more times, i.e. there is a serious divergence of dynamic behavior in model equivalent materials and rocks. The nature of this divergence is in that during sonic tests of specimens the wave is registered which propagates basically through hard grains to define more exactly the behavior pattern of specimens from equivalent materials under strong dynamic impacts special measurements of deformation characteristics were carried out with the use of shock loading of various force and time-duration, and also the measurements with using the specially developed strain gauges of deformations and stresses in specimens. Readings records of strain gauges were made with the use of Kreit LTR-EU-16-1 with tensometric moduli of LTR-212 mark.

Figure 1. Chart of general seismic zoning of the North Eurasia OSR-97 [1] with marked coal opencasts on it.
The most important result of these tests was the following: just under strong shock impact the dynamic elastic characteristics and also the wave velocities are substantially less than in ultrasonic test, and basically they differ from static ones approximately in those relationships as in the modelled rocks. The essence of difference is that heavy dynamic loading incorporates a slow process of pore compression (or air bubbles in three-phase medium) retarding the wave propagation [32]. The higher loading speed, the more deformation processes affect immediately the rock mass (hard skeleton). The less loading speed, the more deformation occurs at the cost of long-term processes of compression of fractures, gas in bubbles, pores and joints, repacking of particles, etc. Intensity of loading, naturally, affects in opposite direction, i.e. high stresses will accelerate inclusion of slow processes that increases their speed, however, these speeds remain much less than speeds of deformation of hard skeleton.
The relationship of examined phenomena in selected materials provides closeness of the relation of their dynamic and static deformation characteristics to the relations of static and dynamic module of rocks (Figure 2) and possible modeling of complicated processes merging the slow and fast loading. Thus, the analogy was established between the behavior of rocks and equivalent materials under dynamic loads (being a particular case of similarity in behavior of fractured and porous media [34,35].
Initial data of modeling (M1: 500) of conditions are shown in Table 1.
3. Results of Experiments
Modeling was carried out by two steps. The aim of the first step was identify the qualitative estimation of the influence pulse duration on displacement sliding triangle. The second step—a quantitative estimation of the influence of seismic effect duration on the slope stability with the development of the subsequent specific recommendations.
At the first step of modeling the influence of loading speed on movement under dynamic impact was studied. The estimation of influence of pulsed loading duration was made on models with circular cylinder sliding plane (Figure 3) by delivering single blows with hammers of various stiffness on strain gauge ring 1, “calibrated on loading”.

Figure 2. Comparison of relationships of elasticity module depending on speed of deformation compression for rocks [33] and equivalent materials: 1, 14—limestone; 2, 11, 12—sandstone; 3, 13—gabbro; 4—granite; 5—concrete; 6—marble; 7—tuff; 8—siltstone; 9—andesite; 10—anthracite; 15—argillite.
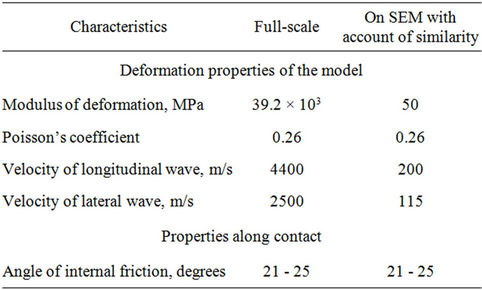
Table 1. Initial full-scale data for modeling.
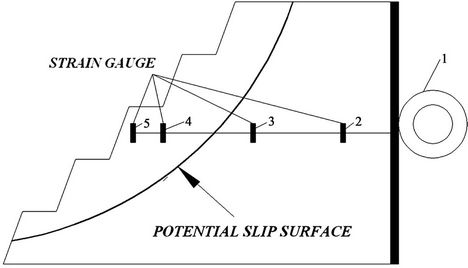
Figure 3. Model with circular slip surface. Numbers indicate strain tensors.
Displacements of collapse prism were recorded with photographic camera. By the results of data treatment, obtained with using the photoand tensiometric measurements, the relationship was obtained of displacements from frequency and blows force (frequency of vibrations induced by blowing effects, with account of similarity conformed to frequencies of seismoexplosive waves). The pulse duration for steel hammer was 0.7 ms, for hard rubber one –1.8 ms and soft rubber one –3.7 ms (Figure 4).
As is seen in Figure 4, the vibrations induced by the forces of equal value with greater duration of pulses, cause more heavy displacements than with shorter pulses. The collapse prism deigns its movement only after overcoming the certain threshold value of internal forces, depending on duration of pulses. Differences between pulses of various duration quantitatively analogous to differences of vibrations in blasting operations and earthquakes. Acceleration in earthquakes is significantly less than in explosions, but most catastrophic aftereffects are observed just during earthquakes. One of basic reasons of this phenomenon is just different period of vibrations.
For estimation of influence of seismic effect duration on the open-pit slope tests were carried out on models with sliding plane in the form of flat inclined contact (Figure 5), as base, the model was chosen with inclination angle 20˚ of sliding plane and calculated safety factor 1.26. Measuring technique was analogous to the tests with individual blows on model with circular cylindrical sliding plane. Modeling of seismic vibrations was made with the use of dynamic impact of cams with various values of eccentricity mounted on the engine shaft with alternating frequency of rotation allowing to reproduce various values of acceleration similar to the intensity range of vibrations in nature. Displacements of collapse prism were recorded with strain gauge in the form of cramp (further cramp-strain gauge), and accelerations induced by blowing impact (with cams) were determined with accelerometers and/or double differentiation of signal of displacement gauge fixed at the glued to model end plane. With changes in rotation frequency and eccentricity value the actual range of accelerations conformed to intensities of seismic vibrations within the range III - VIII.
Practically in all tests the movement began with some retardation after start of vibrations, i.e. “mass” should have time for activation (t2) of mass, in which vibrations cover the whole block and resistance to displacement is overcome induced by irregularity (of fractal structure) of potential slip surface. The time threshold after which the collapse prism sliding down begins, is expressed rather plainly (Figure 6). Respectively, irreversible deformations of slope may begin only after time t2 if the vibratory process terminates earlier, then the earthquake will not induce major irreversible deformations.

Figure 4. Relationship between displacement of collapse prism and the applied value of shock effects of various duration.

Figure 5. Model with flat sliding plane. 1,2,3—numbers of strain gauges.
In analysis of test results the relationship was revealed between the time of preparation t2 and intensity of vibrations (Figure 7, all calculations are made for full-scale values obtained by reverse recalculation with using the transient coefficients of modeling):
 (1)
(1)


Figure 6. Records of strain gauges during block movement in various time scales.

Figure 7. Graph of relationships between time necessary for preparation of sliding-down of collapse prism and intensity of earthquakes.
where a and b are empirical coefficients reflecting the contact conditions between blocks.
For slope with inclination angle 20 degrees of weakening plane and initial factor of slope stability n = 1.26 the coefficients have the following values: а = 1660 and b = –3.34. Points at this graph represent the mean values of preparation time for each value of intensity of vibrations, nibs represent variations with reliability 95%. As is seen in the figure, the values of t2 have a significant spread typical for seismic phenomena.
According to formula [36,37] total duration of vibrations during earthquake depends on its magnitude:
 (2)
(2)
Respectively, with account of formulas (1) and (2) the irreversible deformations will occur, if duration of vibrations exceeds the time of preparation t2. More precise presentation on emergence of irreversible deformations the probabilistic estimations will give—for our base case (n = 1.26) they are presented in Table 2.
Thus, as is seen in this Table, magnitude of an earthquake is of great importance. Vibrations of the same intensity have various influences on slopes, even weak vibrations of level III-IV from remote earthquake of magnitude 7 - 8 with a very high probability will lead to emergence of irreversible deformations.
As in tests vibrations had a quasiharmonic character and nearly constant amplitude, then according to described above Newmark’s approach the orbital velocity of displacement of collapse prism was practically constant (Figure 5). However, pay attention to the fact that in more detailed examination it is seen that movement with each vibration consists of more intensive movement forth and less intensive movement back. Thus, in the experiment no that variant of Newmark’s approach is being observed which was realized in basic programs, but another variant—of two-side movement or, more exactly, some intermediate one between them, but just more close to the two-side movement. In our opinion, realization of just such variant first of all is connected with the presence of forces “elastic output”, developing in movement down, which indeed is not pure through sliding, but some combination of through sliding and deformation of surface sliding. In such case the condition of movement upwards is the following:
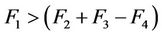 (3)
(3)
where F1—seismic waves; F2—static holding forces; F3—static moving forces; F4—forces of elastic output.
Close analysis of all tests has shown that with various periods of vibrations and different relationships of these forces the movement may have a reciprocating, intermittent or nearly continuous character.
However, the presence itself of irreversible deformations does not yet represent an immediate threat for slope stability, as indicated the investigations of the Institute VNIMI [31,38] irreversible deformations represent danger for slope beginning only with certain values According to formulas (1) and (2), a mean value of irreversible deformations will be:
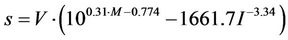 (4)
(4)
where V is mean velocity of displacement.
The obtained mean velocities of displacements are presented in Table 3, relation  was used for their approximation. As is seen in the given formula and data in Table 3, with intensity of vibrations less V a sharp decrease of displacement orbital velocity are observed, therefore it is sufficiently evident that vibrations of level III-IV cannot induce threatening irreversible deformations of slope.
was used for their approximation. As is seen in the given formula and data in Table 3, with intensity of vibrations less V a sharp decrease of displacement orbital velocity are observed, therefore it is sufficiently evident that vibrations of level III-IV cannot induce threatening irreversible deformations of slope.
For more precise estimation of danger of obtained values of displacements the data [31,38] on value of irreversible deformations of slope were used. Based on the analysis of this data, the following typification was set up of probable aftereffects of deformations caused by dynamic impact of seismic waves (Table 4).

Table 2. Probability of emergence of irreversible deformations, %.

Table 3. Mean velocities of vibrations.
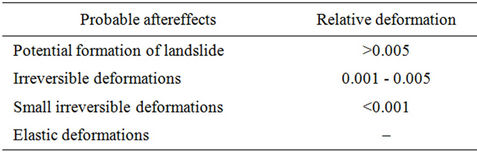
Table 4. Typification of probable aftereffects with various values of relative deformations.
Based on the suggested typification, consider, what aftereffects will emerge in the slope at different distances from epicentre of earthquake. For this purpose we shall use the common equation of microseismic field of crustal earthquakes (equation by N. V. Shebalin) connecting at some point with Intensity shakes Ii, magnitude M, epicentral distance Δ, depth of site of origin h [39,40]:
 (5)
(5)
where b, v, c are constants. For conditions of the AltaeSayansk seismoactive region these coefficients are equal to 1.5, 4.0 and 4.0, respectively [41]. Based on formulas (4) and (5) one can estimate for given conditions the probable aftereffects of crustal earthquakes of different magnitude, Table 5.
For more common estimation of influence of seismic effect on open-pit slope stability additional tests were carried out for slope models with n = 1.13, 1.39 and 2.46, and inclination angles of sliding plane were equal to 22, 18 and 10.5 degrees, respectively. Pseudostatic estimations of safety factor for slope models are presented in Figure 8. As is easily seen, these estimations are very close to the estimates of slope stability for natural conditions (Figure 1). Vibrations with intensity up to level IV-V nearly have no influence on stability that conforms to experimental data (Table 3). It is important to note that according to these estimates to the earthquakes of level IX even the operating slope with safety factor more than 2 would not resist.
Comparison of the obtained data on time of displace-

Table 5. Estimation of probable aftereffects of earthquakes (h < 50 km) of various magnitude for open-pit mine slope with safety factor n = 1.26.

Figure 8. Change in safety factor depending on intensity of earthquake for slopes with n = 1.13, 1.26, 1.39 and 2.46.
ment preparation with calculated safety factors has shown a sharp decrease of time of preparation with small and moderate intensity of vibrations and begins in the vicinity of the field of approximate equality of holding and moving forces,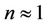 . For example, for intensity of level VII a sharp decrease in preparation duration up to 1 sec. and below takes place with original value of n within 1.2, i.e. for pseudostatic safety factor about 0.9. At the same time for vibrations of level VIII the preparation time already substantially diverges with pseudostatic calculation—time delay threshold of 1 sec. is overcome with n = 0.6.
. For example, for intensity of level VII a sharp decrease in preparation duration up to 1 sec. and below takes place with original value of n within 1.2, i.e. for pseudostatic safety factor about 0.9. At the same time for vibrations of level VIII the preparation time already substantially diverges with pseudostatic calculation—time delay threshold of 1 sec. is overcome with n = 0.6.
Figure 9 shows graphs of displacements for slopes with different initial safety factor under various intensity of vibrations for earthquakes of magnitudes 6 and 8.