1. Introduction
Population dynamics in ecology are generally governed by discrete and continuous systems. In recent years, the study of discrete ecological systems has attracted extensive attentions [1-6]. This is because that some natural populations have non-overlapping generations, thus discrete models are more realistic than continuous ones to study these species. Another reason is that people always study population changes by one year (mouth, week or day). Such investigations are often required discrete models. Especially, using discrete models is more efficient for numerical simulations. Recently, Zhang and Li [1] studied the following discrete ecological model:

 (1)
(1)
where xn, yn denote the two ecological species’ densities respectively in generation n; δ is the integral step size. The more meaning of system (1) can refer to the reference [1,2]. It is shown that the system (1) generates period-double bifurcations and chaos. But the authors did not investigate the chaos control of the system.
It is well known that chaos control is the first step of utilizing chaos. The possibility of chaos control in biological systems has been stimulated by recent advances in the study of heart and brain tissue dynamics. Recently, some authors have investigated that such a method can be applied to population dynamics and even play a nontrivial evolutionary role in ecology [7-9]. In this paper, we design a proper controller to control the chaos of system (1).
2. Chaos Control
In this section, chaotic orbits to an unstable fixed point are stabilized by utilizing some control techniques. Firstly, we introduce the following lemma which is useful to establish our results Lemma 1 [1]. If a > b, then system (1) has an unique positive fixed point at , where
, where ,
, .
.
Consider the following map which is the feedback is applied to system (1)
 (2)
(2)
where Xn = (xn, yn)T, μn is control variable and satisfies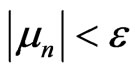 ,
, . Evidently, map (2) degenerates to original system (1) only if μn = 0. We select the feedback variable μn in the range (–ε, ε), so that the orbit holds in the neighborhood of fixed point E as long as the control arises. The ergodic nature of the chaotic dynamics guarantees that the mode trajectory in the neighborhood of the wishful orbit
. Evidently, map (2) degenerates to original system (1) only if μn = 0. We select the feedback variable μn in the range (–ε, ε), so that the orbit holds in the neighborhood of fixed point E as long as the control arises. The ergodic nature of the chaotic dynamics guarantees that the mode trajectory in the neighborhood of the wishful orbit . In the neighborhood of E, map (2) can be approximated by the following form:
. In the neighborhood of E, map (2) can be approximated by the following form:
 (3)
(3)
where A is the Jacobian matrix at E and B is a column vector, and they are given by:
 ,
,
 .
.
Let X* = (x*, y*)T and suppose that μn is a linear function of Xn, which is expressed as μn = PT(Xn – X*), . Substitute the result into (3), we get
. Substitute the result into (3), we get
 .
.
According to the study [10], the fixed point E will be stable if the matrix (A – BPT) is asymptotically stable, that is to say, all its eigenvalues are less than 1 in modulus. Now, we make use of “pole placement technique” [11] to determine the specific values in (A – BPT). If system (1) is chaotic, we obtain
 .
.
Then we choose 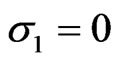 ,
, 
as the desired eigenvalues of the matrix (A – BPT). The controllability matrix

has two rank. Thus the solution to the pole placement problem is obtained as
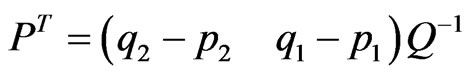 where Q = CW,
where Q = CW, 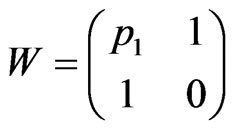 p1 and p2 are the coefficients of characteristic polynomial of the matrix A,
p1 and p2 are the coefficients of characteristic polynomial of the matrix A,  and
and  ,
,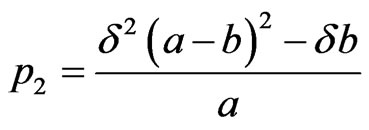 ;
;
q1 and q2 are the coefficients of characteristic polynomial of the matrix (A – BPT),
 and
and  , q2 = 0.
, q2 = 0.
After calculations, we get
 (4)
(4)
Furthermore, the controller has the following form:
 where
where ,
, .
.
However, the above considerations only are fit for a local small neighbor of E. In view of the global situationwe can specify μn by making μn = 0 if 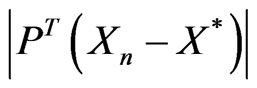
is too large. This is because the range of μn is restrained by  and
and . Thus, we limit the number value
. Thus, we limit the number value
 .
.
Therefore, in practice we take μn as
 (5)
(5)
According to the above analysis, we get the following result.
Theorem 1. If  then the control variable
then the control variable  can stabilize chaotic trajectory of system (1) to the fixed point E, where PT is given by Equation (4).
can stabilize chaotic trajectory of system (1) to the fixed point E, where PT is given by Equation (4).
3. Numerical Simulations
In the section, we use density-time diagrams and phase portraits to confirm the above theoretical analysis.
Let a = 2.21, b = 1.02, δ = 0.9666. At the condition,  has the value 7.70732. According to Lemma 1, system (1) has and only has a positive fixed point E(x*, y*) = (2.16667, 0.53846). We adopt
has the value 7.70732. According to Lemma 1, system (1) has and only has a positive fixed point E(x*, y*) = (2.16667, 0.53846). We adopt
 .
.
When ε is given the value 0.03 and 0.09, Theorem 1 is satisfied. Density-time diagram of ecological specie xn is given by Figure 1(a), which is characterized by switches between apparently regular and chaotic behaviors. Actually, it is intermittency, which is a basic characteristic of chaos. At the same parameters, phase portrait is illustrated by Figure 1(b), which is a chaotic attractor. Figure 2 is the chaos control diagrams corresponding to Figure 1. With the same parameters of Figure 1, system (1) is chaotic if n < 800 when ε = 0.03 (Figures 2(a) and (b)) according to the control strategy. Actually, Figure 2(a) is supertransient, which is used to denote an unusually long convergence to an attractor. Figure 2(b) is phase portrait corresponding to Figure 2(a). When ε increases to 0.09, supertransient disappears and the system
 (a)
(a) (b)
(b)
Figure 1. (a) Density-time diagram of xn; (b) phase portrait of xn and yn. Where the parameters given by a = 2.21, b = 1.02, δ = 0.9666.
stabilizes to the fixed point (2.16667, 0.53846), which is simulated by Figures 2(c) and 2(d).
4. Conclusion
In this paper, we design a proper controller to control the chaos of system (1) which was firstly studied by Zhang and Li [6]. From the theoretical analysis, we concluded that the control variable  can stabilize chaotic trajectory of system (1) to the fixed point E(x*, y*) under the condition of
can stabilize chaotic trajectory of system (1) to the fixed point E(x*, y*) under the condition of
 where PT is given by Equation (4). Then simulations are presented to show the correctness of theoretical analysis. Figure 1 demonstrates system (1) is chaotic with parameters a = 2.21, b = 1.02, δ = 0.9666. Figure 2 indicates system (1) processes from supertransient to the fixed point when the control variable applied to the system.
where PT is given by Equation (4). Then simulations are presented to show the correctness of theoretical analysis. Figure 1 demonstrates system (1) is chaotic with parameters a = 2.21, b = 1.02, δ = 0.9666. Figure 2 indicates system (1) processes from supertransient to the fixed point when the control variable applied to the system.
5. Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 30970305), the Sichuan Provincial Natural Science Foundation (No. 10ZB136), the Sichuan Provincial Old Revolutionary Base Areas Foundation (No. SLQ2010C-17).
NOTES