Nonlinear Spinor Field Equations in Gravitational Theory: Spherical Symmetric Soliton-Like Solutions ()
1. Introduction
The unification of quantum mechanics and general relativity into a theory of quantum gravity remains a hard (as yet) unsolved problem and physical phenomena requiring both general relativity and quantum theory for their description cannot be possibly completely understood. Such a challenge stimulates intense research activities in various field-theoretical models with full non-perturbative account of gravity. Among all these activities, the investigations of solitons in these theories, with a special emphasis on flat space theories, attracted a particular importance due to their properties. Indeed, the soliton sector in the flat space gauge theories is quite well understood, the most notable example being the t’Hooft-Polyakov magnetic monopole. For a review on some recent progress in the investigation of solitons and black holes in non-Abelian gauge theories coupled to gravity, see [1] and references therein. However, as is well known, the marriage of gravity and relativity leads to a curved spacetime whose geometry is dynamical and is governed by the energy-matter distribution within it, a framework within which the gravitational interaction is the physical manifestation of any curvature in space and in space-time. The most fascinating offsprings of this union are undoubtedly, on the one hand, the cosmological theory of the history of our universe from its birth to its ultimate demise if ever, and on the other hand, the prediction for regions of space-time to be so much curled up by their energy-matter content that even light can no longer escape from such black holes.
On the other hand, the marriage of relativity and quantum theory leads naturally to the quantum field theory description of the elementary particles and their interactions, at the most intimate presently accessible scales of space and energy, a fact made manifest by the value of the product  Mev.fm. In fact, one offspring of this second union is the unification of matter and radiation, namely of particles with their corpuscular propagating properties and fields with their wavelike propagating properties. Particles, characterized through their energy, momentum and spin values in correspondence with the Poincaré symmetries of Minkowski space-time in the absence of gravity, are nothing but the relativistic energy-momentum quanta of a field, thereby implying a tremendous economy in the description of the physical universe, accounting for instance at once in terms of a single field filling all of space-time for the indistinguishability of identical particles and their statistics. Furthermore, quantum relativistic interactions are then understood simply as couplings between the various quantum fields locally in space-time, which translate in terms of particles as diverse exchanges of the associated quanta. Such a picture lends itself most ideally to a perturbative understanding of the fundamental interactions, which has proved to be so powerful beginning with quantum electrodynamics, up to the modern Standard Model of the strong and electroweak interactions. For more explanation on these profound concepts, quantum theory and relativity, which have culminated into relativistic spacetime geometry and quantum gauge theory as the principles for gravity and the three other known fundamental interactions, see notes [2] on The quantum geometer’s universe: Particles, interactions and topology delivered in 2001 by Govaerts at the Second International Workshop on Contemporary Problems in Mathematical Physics.
Mev.fm. In fact, one offspring of this second union is the unification of matter and radiation, namely of particles with their corpuscular propagating properties and fields with their wavelike propagating properties. Particles, characterized through their energy, momentum and spin values in correspondence with the Poincaré symmetries of Minkowski space-time in the absence of gravity, are nothing but the relativistic energy-momentum quanta of a field, thereby implying a tremendous economy in the description of the physical universe, accounting for instance at once in terms of a single field filling all of space-time for the indistinguishability of identical particles and their statistics. Furthermore, quantum relativistic interactions are then understood simply as couplings between the various quantum fields locally in space-time, which translate in terms of particles as diverse exchanges of the associated quanta. Such a picture lends itself most ideally to a perturbative understanding of the fundamental interactions, which has proved to be so powerful beginning with quantum electrodynamics, up to the modern Standard Model of the strong and electroweak interactions. For more explanation on these profound concepts, quantum theory and relativity, which have culminated into relativistic spacetime geometry and quantum gauge theory as the principles for gravity and the three other known fundamental interactions, see notes [2] on The quantum geometer’s universe: Particles, interactions and topology delivered in 2001 by Govaerts at the Second International Workshop on Contemporary Problems in Mathematical Physics.
All these activities, diverse and complementary, made in this field [1-14], are also mainly motivated by the wide roles of Einstein and Dirac equations in modern physics, for example, for investigating the spin particle and for the necessity of analysis of synchrotronic radiation [11]. To this purpose, many systems have been subjects of considerable interest and studies. The pioneering investigation could be the work by Drill and Wheeler in 1957 [3], who considered the Dirac equation in a central gravitational field associated with a diagonal metric. Using a normal diagonal tetrad, these authors constructed the generalized angular momentum operator separating the variables in the Dirac equation. Later, in a remarkable paper, appeared in 1987 [12], entitled “Criteria of separability of variables in the Dirac equation in gravitational fields”, Shishkin and Andrushkevich provided the necessary and sufficient conditions, based on rigorous theorems, for separability of the variables for a diagonal tetrad gauge, and deduced the operators that determine the dependence of the wave function on the separated variables. In the same year, Barut and Duru [10] gave exact solutions of the Dirac equation in spatially flat Robertson-Walker space-times for models of expanding universes and discussed the current decomposition. Henceforth the investigations go into diverse directions, considering various classes of models including different metrics, the general class of which is investigated by Hounkonnou and Mendy in 1999 [13]. Thus, for example, the usual Friedman-Lemaître-Roberston-Walker homogeneous and isotropic metric of standard cosmology belongs to this general class of metrics (whether in Cartesian or spherical coordinates), which also includes general classes of Kantowski-Sachs metrics for anisotropic cosmologies as well as some examples of metrics used in models for stellar gravitational collapse [14]. It may be worth pointing out that a priori, this class of metrics solves Einstein’s equations for specific distributions of energy-momentum of matter in space-time, in the presence of which the study of the quantized Dirac field may be of interest. Such an avenue could be pursued. For details, see [13] and references therein.
Moreover, it is also worthy of attention a previous study, which will be referred to Part I of the present work, where Adomou and Shikin [8] have obtained exact plane-symmetric solutions to the spinor field equations with nonlinear terms which are arbitrary functions of , taking into account their own gravitational field. They have studied in detail equations with power and polynomial nonlinearities. They have shown that the initial set of the Einstein and spinor field equations with a power-law nonlinearity has regular solutions with a localized energy density of the spinor field only in the case of zero mass parameter in the spinor field, with a negative energy for the soliton-like configuration. They have also proved that the spinor field equation with a polynomial nonlinearity has a regular solution with positive energy. Their study has come out onto the non existence of soliton-like solutions in the flat space-time.
, taking into account their own gravitational field. They have studied in detail equations with power and polynomial nonlinearities. They have shown that the initial set of the Einstein and spinor field equations with a power-law nonlinearity has regular solutions with a localized energy density of the spinor field only in the case of zero mass parameter in the spinor field, with a negative energy for the soliton-like configuration. They have also proved that the spinor field equation with a polynomial nonlinearity has a regular solution with positive energy. Their study has come out onto the non existence of soliton-like solutions in the flat space-time.
The present work, considered as Part II of all these investigated initiated in [8], aims at extending the results to exact spherical symmetric solutions. Here also equations with power and polynomial nonlinearities are thoroughly scrutinized.
The paper is organized as follows. Section 2 addresses the model with fundamental equations. We consider a selfconsistent system to obtain spherical-symmetric solutions, taking into account the own gravitational field of particles. Section 3 deals with main results and their discussion; the solutions of the Einstein and nonlinear spinor field equations are derived. Besides, the regularity properties of the obtained solutions as well as the asymptotic behavior of the energy and charge densities are studied. Concluding remarks are outlined in Section 4.
2. Model and Fundamental Equations
We consider the Lagrangian of the self-consistent system of spinor and gravitational fields in the form [8]:
 (2.1)
(2.1)
 (2.2)
(2.2)
where R is the scalar curvature; 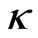 is Einstein’s gravitational constant and
is Einstein’s gravitational constant and  is an arbitrary function depending on
is an arbitrary function depending on .
.
Instead of the static plane-symmetric metric chosen in [8], in the present analysis we opt for the static spherical symmetric metric in the form:
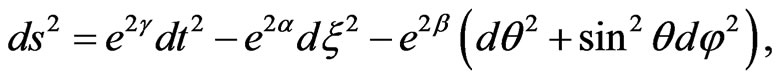 (2.3)
(2.3)
 being some functions depending only on
being some functions depending only on where r stands for the radial component of the spherical symmetric metric, and satisfying the coordinate condition
where r stands for the radial component of the spherical symmetric metric, and satisfying the coordinate condition
 (2.4)
(2.4)
From the Lagrangian (2.1), through the variational principle and usual algebraic manipulations, one can readily deduce the Einstein equations for the metric (2.3) under the condition (2.4), the spinor field equations for the functions ,
,  , and the components of the metric spinor field energy-momentum tensor, respectively, in the form [3]:
, and the components of the metric spinor field energy-momentum tensor, respectively, in the form [3]:
 (2.5)
(2.5)
 (2.6)
(2.6)
 (2.7)
(2.7)
 (2.8)
(2.8)
 (2.9)
(2.9)
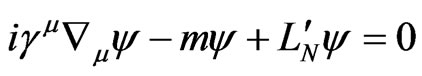 (2.10)
(2.10)
 (2.11)
(2.11)
 (2.12)
(2.12)
where  is the covariant spinor derivative [3]:
is the covariant spinor derivative [3]:
 ;
;  are the spinor affine connection matrices. To define the matrices
are the spinor affine connection matrices. To define the matrices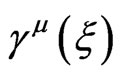 , let us use the equalities
, let us use the equalities
 (2.13)
(2.13)
where ;
;  are the Dirac’s matrices in flat space-time;
are the Dirac’s matrices in flat space-time; 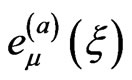 are tetradic 4- vectors. Then we get:
are tetradic 4- vectors. Then we get:
 (2.14)
(2.14)
The matrices 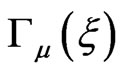 are then determined as follows:
are then determined as follows:
 (2.15)
(2.15)
 (2.16)
(2.16)
 (2.17)
(2.17)
The matrices  are chosen as in [3]. Using the spinor field equations, we can rewrite
are chosen as in [3]. Using the spinor field equations, we can rewrite  in the form
in the form
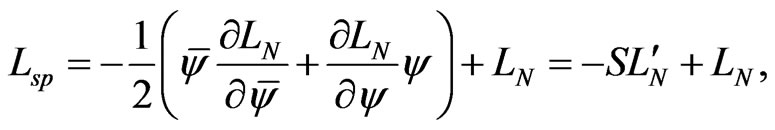 (2.18)
(2.18)
with the spinor

Taking into account (2.18), let us write explicitly the nonzero components of the tensor :
:
 (2.19)
(2.19)
setting the condition ,
,
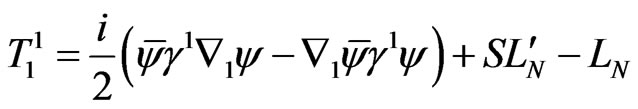 (2.20)
(2.20)
Using the obtained expressions for  in (2.15)- (2.17), we can expand (2.10) as
in (2.15)- (2.17), we can expand (2.10) as
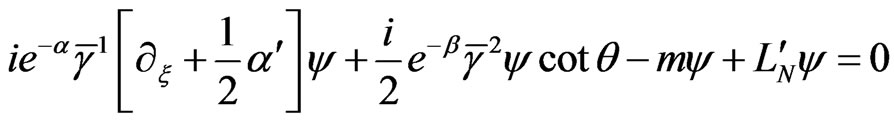 (2.21)
(2.21)
yielding the following set of equations:
 (2.22)
(2.22)
 (2.23)
(2.23)
 (2.24)
(2.24)
 (2.25)
(2.25)
3. Results and Discussion
From the set of Equations (2.22)-(2.25), we infer that the invariant function

satisfies a first order differential equation:
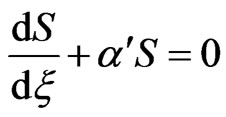 (3.1)
(3.1)
giving the evident solution
 (3.2)
(3.2)
C being a constant. Combining the spinor field Equation (2.21) with its conjugate expression results the following expression for (2.20):
 (3.3)
(3.3)
The difference  of the Einstein equations with (2.19) leads to
of the Einstein equations with (2.19) leads to
 (3.4)
(3.4)
which can be transformed into a Liouville equation (see [7], page 30) to produce the solutions:
 (3.5)
(3.5)
 (3.6)
(3.6)
where the quantity A is expressed in terms of the Newton’s gravitational constant G as:
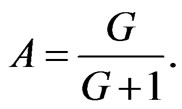
 (3.7)
(3.7)
h being an integration constant and  another non zero integration constant. Taking into account (3.5) and (3.6), we get from (2.4) the following relations:
another non zero integration constant. Taking into account (3.5) and (3.6), we get from (2.4) the following relations:
 (3.8)
(3.8)
and
 (3.9)
(3.9)
Substituting (3.8) into (2.6), we obtain the Einstein equation  in the form
in the form
 (3.10)
(3.10)
Since  with the invariant
with the invariant , from (3.10), we get:
, from (3.10), we get:
 (3.11)
(3.11)
With the knowledge of  and
and  from the relations (3.5), (3.6) and (3.8), respectively, the invariant
from the relations (3.5), (3.6) and (3.8), respectively, the invariant  as well as the solutions of the Einstein equations can be completely determined. Furthermore, considering the concrete expression of the invariant
as well as the solutions of the Einstein equations can be completely determined. Furthermore, considering the concrete expression of the invariant , namely
, namely , we can establish the regularity properties of the obtained solutions. Studying the distribution of the energy per unit invariant volume
, we can establish the regularity properties of the obtained solutions. Studying the distribution of the energy per unit invariant volume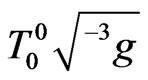 , we can also deduce their localization properties.
, we can also deduce their localization properties.
We can get a concrete form of the functions  by solving Equations (2.22)-(2.25) in a more compact form if we pass to the functions
by solving Equations (2.22)-(2.25) in a more compact form if we pass to the functions , ρ = 1, 2, 3, 4:
, ρ = 1, 2, 3, 4:
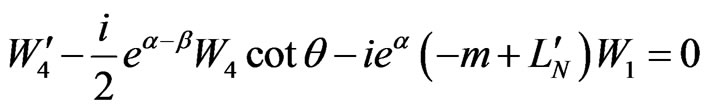 (3.12)
(3.12)
 (3.13)
(3.13)
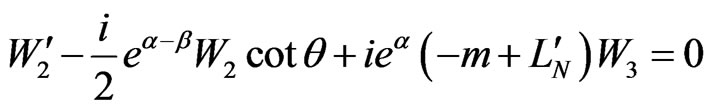 (3.14)
(3.14)
 (3.15)
(3.15)
where
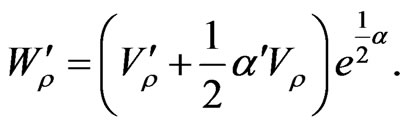 (3.16)
(3.16)
Re-express Equations (3.12)-(3.15) under forms depending on functions of the argument , i.e.
, i.e. 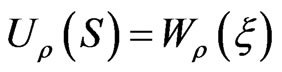 ,
,  Then we get for the functions
Then we get for the functions 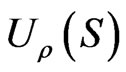 the following set of equations:
the following set of equations:
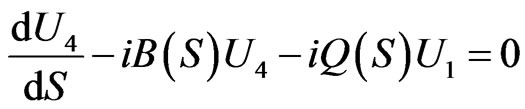 (3.17)
(3.17)
 (3.18)
(3.18)
 (3.19)
(3.19)
 (3.20)
(3.20)
where
 (3.21)
(3.21)
with  determined by (3.11).
determined by (3.11).
Differentiating now Equations (3.17)-(3.20) and substituting Equations (3.20) and (3.17) into the result, we obtain second-order differential equations obeyed by the functions  and
and :
:
 (3.22)
(3.22)
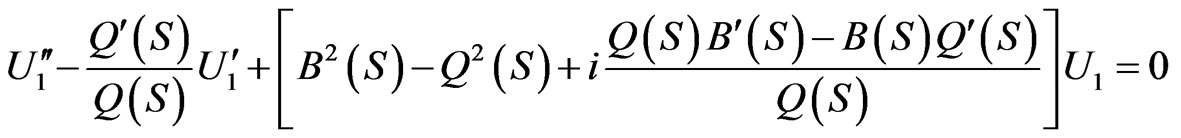 (3.23)
(3.23)
Summing (3.22) and (3.23) and setting 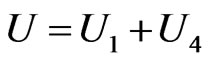 afford the differential equation:
afford the differential equation:
 (3.24)
(3.24)
which, under the condition 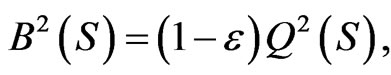 with
with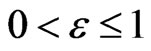 , yields the solution
, yields the solution
 (3.25)
(3.25)
where . Substracting Equations (3.17) and (3.20) and taking into account (3.25), we obtain
. Substracting Equations (3.17) and (3.20) and taking into account (3.25), we obtain
 (3.26)
(3.26)
It then follows, from the Equations (3.25) and (3.26), that
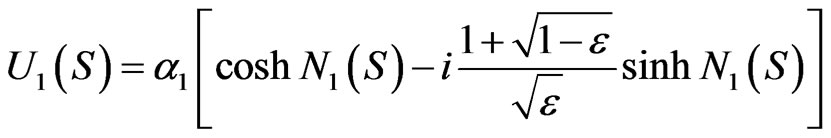 (3.27)
(3.27)
and
 (3.28)
(3.28)
with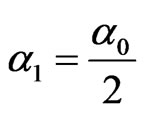 .
.
Analogously operating on Equations (3.18) and (3.19), we arrive at
 (3.29)
(3.29)
and
 (3.30)
(3.30)
with ,
,
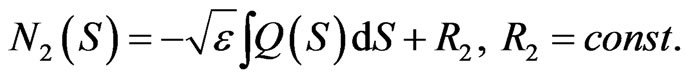 (3.31)
(3.31)
As mentioned in [8], it is worth considering a selfconsistent solution to the linear spinor field equation (Dirac’s equation), in view of its comparison with solutions to nonlinear spinor equations and of a better insight of the role of nonlinear terms in the nonlinear field equations in the formation of regular localized soliton-like solutions. For this purpose,  and we have from (2.21):
and we have from (2.21):
 (3.32)
(3.32)
In this case, the relation (3.32) giving  becomes:
becomes:
 (3.33)
(3.33)
From (3.5), (3.6) and (3.8), we get:
 (3.34)
(3.34)
 (3.35)
(3.35)
 (3.36)
(3.36)
showing that the invariant S and the functions ,
, 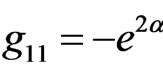 ,
,  ,
,  are regular. In the case under consideration we have
are regular. In the case under consideration we have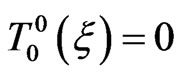 , i.e. the energy density is localized.
, i.e. the energy density is localized.
Using (3.11), (3.21) and (3.31), we get:
 (3.37)
(3.37)
with .
.
Let us find the explicit form of . To this end, we retrieve the expressions of
. To this end, we retrieve the expressions of  and
and 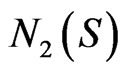 from (3.37), knowing that
from (3.37), knowing that . Without loss of generality, let us set
. Without loss of generality, let us set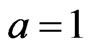 . Then,
. Then,
 (3.38)
(3.38)
Substituting  from (3.33) into (3.38), we get
from (3.33) into (3.38), we get
 (3.39)
(3.39)
with .
.
We then replace the expressions of  and
and  from (3.39) into (3.27)-(3.30) and get an explicit form of
from (3.39) into (3.27)-(3.30) and get an explicit form of , and subsequently the expressions of
, and subsequently the expressions of
 :
:
 (3.40)
(3.40)
 (3.41)
(3.41)
 (3.42)
(3.42)
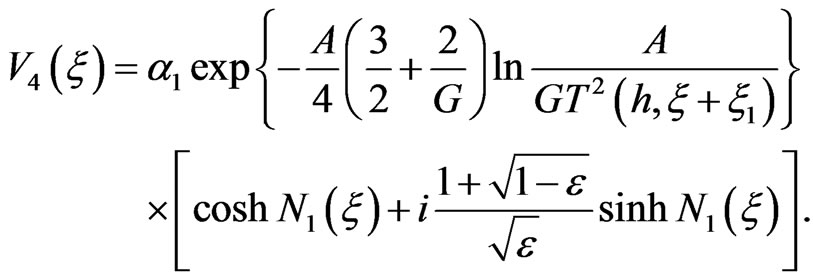 (3.43)
(3.43)
which represent nothing but the regular localized solitonlike solutions.
In the sequel, we deal with a concrete type of nonlinear spinor field equations which have the virtue that , where
, where  is a nonlinearity parameter,
is a nonlinearity parameter, . It is convenient to separately analyze the two cases
. It is convenient to separately analyze the two cases 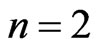 and
and :
:
•  :
: 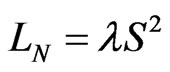 and we have the nonlinear spinor field equation
and we have the nonlinear spinor field equation
 (3.44)
(3.44)
The equalities (3.33)-(3.36) remain valid. Let us find an explicit form of . For that, we deduce from (3.37) the function
. For that, we deduce from (3.37) the function  and
and :
:
 (3.45)
(3.45)
that we substitute into (3.27)-(3.30) to get an explicit expression of 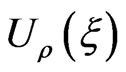 and subsequently the initial functions
and subsequently the initial functions ,
,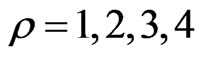 .
.
Let us compute the distribution of the spinor field energy density per unit invariant volume  . From (2.19) and (3.33) we have the following expression for
. From (2.19) and (3.33) we have the following expression for :
:
 (3.46)
(3.46)
permiting to write
 (3.47)
(3.47)
inferring that the quantities ,
,  ,
,  and
and  are regular and, from (3.47), the total energy
are regular and, from (3.47), the total energy
 is finite. Therefore, the equation
is finite. Therefore, the equation
(3.44) possesses a soliton-like solution.
•  :
:  and the energy density is
and the energy density is
 (3.48)
(3.48)
From (3.33), the distribution of the spinor field energy density per unit invariant volume takes the form

i.e.
 (3.49)
(3.49)
showing that the spinor field energy density per unit invariant volume f is localized and the total energy  is finite. To compute
is finite. To compute ,
, 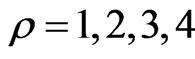 , we need the functions
, we need the functions 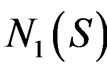 and
and :
:
 (3.50)
(3.50)
where
 (3.51)
(3.51)
and
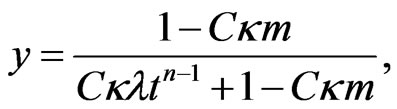 (3.52)
(3.52)
that we substitute into (3.27)-(3.30) to get an explicit expression for , and then we readily compute the initial functions
, and then we readily compute the initial functions
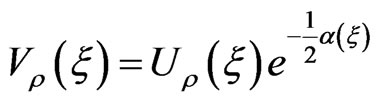 (3.53)
(3.53)
for . Using the solutions (3.27)-(3.30), we deduce the components of the spinor current vector
. Using the solutions (3.27)-(3.30), we deduce the components of the spinor current vector  as follows:
as follows:
 (3.54)
(3.54)
Since the configuration is static, only the component  is nonzero. The constants in the solution of the spinor field equation are obtained from the equations
is nonzero. The constants in the solution of the spinor field equation are obtained from the equations  and
and , thus giving
, thus giving ,
,  and
and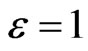 . The component
. The component  defines the charge density of the spinor field whose the chronometric invariant form is characterized by:
defines the charge density of the spinor field whose the chronometric invariant form is characterized by:
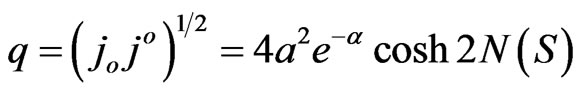 (3.55)
(3.55)
where . The total charge of the spinor field is:
. The total charge of the spinor field is:
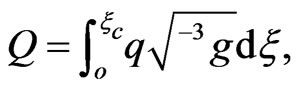 (3.56)
(3.56)
 being the center of the field configuration.
being the center of the field configuration.
The relations (3.33), (3.39), (3.45), (3.55) and (3.56) infer that the charge density of the spinor field is localized, and the total charge is a finite quantity, when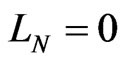 , or
, or , or
, or .
.
4. Concluding Remarks
In this paper, we have obtained exact spherical symmetric solutions to the spinor and gravitational field equations and studied their regularity properties as well as the localization properties of both the energy and charge densities in different configurations, when ,
,  and
and .
.
In all these cases, the solutions are regular; the energy and charge densities are localized. The total energy and charge of the spinor field are finite quantities. The study of the set of all regular spherical solutions with a possible criterion of their classification could deserve some interest. Such investigation will be in the core of the forthcoming paper.
5. Acknowlegements
This work is partially supported by the Abdus Salam International Centre for Theoretical Physics (ICTP, Trieste, Italy) through the OEA-ICMPA-Prj-15. The ICMPA is in partnership with the Daniel Iagolnitzer Foundation (DIF), France.
NOTES