A Genetic Algorithm for Ship Routing and Scheduling Problem with Time Window ()
1. Introduction
The steady growth in international trade over many years has resulted in an increased need for freight transportation. Maritime transportation (seaborne) is the major conduit of international trade. The statistics provided in UNCTAD [1] demonstrate high dependence of the world economy on seaborne trade. It supports production, trade, and consumption activities by ensuring the efficient movement and timely availability of raw materials and finished goods. According to the statistics provided in [1] (see Table 1), the total international seaborne has increased extremely, in terms of weight since 1970. This increase in seaborne trade has resulted in a parallel grown in the world maritime fleet. A recent survey on ship scheduling research is given in Christiansen et al. [2]. Transportation planning has been widely discussed in the literature but most of the attention has been devoted to aircraft, rail and road transportation. Although these modes of transportation have similarities in terms of scheduling, ship fleet planning problems are different than those of other modes of transportation because ships operate under different conditions or operational characteristics. Christiansen et al. [3] conducted a thorough survey of maritime transportation and ship scheduling research.
There are three basic modes of operation of comercial ships; 1) liner, 2) tramp, and 3) industrial Lawrence [4]. Liners operate according to a published itinerary and schedule similar to a bus line. Tramp ships follow the available shipments, like a taxi. A tramp shipping company may have a certain amount of contract shipments that it is committed to carry, and tries to maximize the profit from optional shipments. In industrial shipping, the shippers, control the ships and they strive to minimize the cost of shipping their shipments. In industrial shipping all shipments have to be allocated to a ship and picked up at its origin and delivered at its destination. In some cases, the controlled fleet may have insufficient
capacity to deliver all shipments for an industrial ship scheduling during the planning horizon. In such a case some of the shipments can be delivered by spot charters, which are ships chartered for a single journey. The industrial shipping can be presented into two separate types: inventory routing and cargo routing problems. First, inventory routing problems are constrained by inventory requirements, where the level of products at ports should be maintained. The second type, routing problems are usually constrained by the shipment, which is specified by loading/ unloading ports, and by time windows for loading and unloading. In this paper, the problem can be categorized as industrial shipping for type cargo routing problems. During the last decades, there has been a shift from industrial to tramp shipping, Christiansen et al. [3].
Ship Routing and Scheduling Problem (SRSP) is a branch of OR which focuses on studying and finding the best method to minimize the cost of shipping quantities of shipments over fleet of ships to a number of destinations over time windows. The problem is considered NP-difficult (nun polynomial) and grows in complication proportional to the increase in variables and constraints. The SRSP has been tackled in the literature for industrial shipping through many approaches. The methods varied from exact approach to constructive heuristic. The exact approaches include; integer programming , mixed integer programming, or linear programming, where optimal solution will be produced. On the other hand, it will be complicated to solve large scale problems due to computational problems. The majority of researchers use exact approach methods based on a set partitioning formulation. All candidates feasible schedules are generated a priori, then the scheduling problem is formulated and solved as set partitioning problem. But, for some real ship scheduling problems—large scale—it is time consuming to generate all these schedules, as the number of such schedules would result in too many columns when solving the models. The other technique is constructive heuristic, which capable of solving large scale problem, however, optimality is not guaranty. Examples of heuristic methods; Tabu Search (TS), Genetic algorithm (GA), Simulating Annealing (SA), or Neural Network methods for optimization.
Most of the works in industrial mode are focused on inventory routing, where there are a little works tackled cargo routing as our problem. For example, Christiansen et al. [5] and Ronen [6] considered an inventory routing problem (IRP). On the other hand, Sherali et al. [7] tackled cargo routing problem . They considered a problem for routing and scheduling ships. The main thrust of the research was focused on the Kuwait Petroleum Corporation (KPC) Problem. A fleet of ships was involved in delivering crude oil and refined oil-related products from Kuwait to ports around the world. The model considered a fleet of ships consisting of controlled and chartered ships. The problem was solved and formulated using an integer programming model. The results presented a good cost reduction compared with the ad-hoc schedule procedure used by Kuwait Petroleum Corporation (KPC). Alhamad [8] addressed SRSP using Tabu Search heuristic method. The problem of loading shipments for many customers using heterogeneous ships. Constraints relate to delivery time windows imposed by customers, the time horizon by which all deliveries must be made and ship capacities. The results of a computational investigation are presented. Solution quality and execution time are explored with respect to problem size and parameters controlling of Tabu Search such as tenure and neighbourhood size. Mehrez et al. [9] considered a real industrial ocean cargo-shipping problem. The number and size of ships (controlled and chartered) in each time period are among the decisions to make in addition to the number and location of transshipment ports to use and the transportation routes from discharging ports to customers. The resulting formulation of the problem was a mixed-integer program. They use commercial optimization software to solve the problem by reduce the large scale, dynamic and stochastic problem to a deterministic model. Brown et al. [10] considered a crude oil tanker scheduling problem faced by a major company, and solved it using an elastic set-partitioning model. The oil company controlled several crude oil ships of similar sizes to ship crude oil (full shipload) from Middle East to North America and Europe. The problem was solved by generating all feasible schedules, and selecting the optimal subset of schedules. The model took into account all fleet cost components, and determined the optimal speed for the ships, and the best routing of empty ships. The model also determined which shipments to load on controlled ships, and which to spot charter. Bausch et al. [11] expanded the Brown et al. [10] model for scheduling shipments of refined oil products from several refineries to multiple destinations using either tankers or barges. A microcosmputer system was designed with an EXCEL user interface. A detailed cost model was integrated in the system. The model can be used to find out the optimal speed of the ships and the need for spot chartering ships.
The purpose of this paper is to present a solution approach for this problem based on Genetic Algorithm (GA). GA was used in many other problems and found to produce competitive results; see for example Liu et al. [12]. To the authors knowledge, no work on ship routing and scheduling problem adapted GA is reported in the literature.
In this paper, GA heuristic method is used to solve SRSP with time-window. The method was developed to address the problem of loading shipments for many customers using heterogeneous ships. Besides, the aim of this research is to design a reliable model, which is capable of generating a good schedule for industrial sectors. Moreover, this model can be used to solve large-scale problems practically and efficiently. Yet, an improvement of GA to solve these types of problems was proposed by changing the way of generating population by using insert trail method to repair any infeasible solution. On the other hand, an exact approach based on SPP were presented as well, to measure the quality of the solution for GA used in this paper.
The paper is organized as follows: Section 2, a description of GA is provided in brief. Section 3, problem description and mathematical formulation of the SRSP are described. In Section 4, the proposed algorithm using GA method is presented. The overall computational results are listed and described in Section 5. Finally, conclusions are drawn in Section 6.
2. Genetic Algorithm
This section presents a full description of the GA method, which is capable of solving large scale instances of SRSP. However, since this is a heuristic method, optimality is not guaranteed in all cases.
Genetic Algorithms (GAs) were introduced and developed by Holland [13], his colleagues, and his students at the University of Michigan. The aim of their study was to abstract and explain the adaptive technique of natural systems and to create artificial systems software that preserves the essential mechanisms of natural systems. The idea behind GAs is well known. The application of solutions is generated randomly and reproductive operation allows the parent solutions to be chosen from the population. The GA keeps a population of candidate members over many generations. The population consists of a number of strings of artificial chromosomes. A chromosome consists of a number of entities known as genes. The number of genes in a chromosome is usually the same for all chromosomes in the population. Each gene has a value associated with it. In most applications those numbers are either binary or integer. Variables are often called genes, and the values of variables are called alleles. The process starts by selecting parents according to the fitness value (quality). Offspring solutions are produced by applying two major tools in GA, crossover and mutation.
The first step of most researches that use GA is to generate a number of chromosomes considered as a population or mating pool. Then two chromosomes are selected from the population. By applying the crossover and the mutation operators two Offspring are produced and their fitness is evaluated. This operation will carry on by selecting two other parents from the population and repeat the same previous procedure for a number of iterations or a certain stop criteria is achieved. In contrast, in this research, two chromosomes (parents) will be generated and apply mating operation (crossover and mutation operators) on them to produce a new two Offspring. These two Offspring after evaluation will be considered as a new two parents for the next iteration and then apply the same previous procedure. This operation will carry on for a number of iteration. It is worth noting that, since this is a heuristic method, the optimality is not guaranteed in all cases.
3. Problem Descriptions and Mathematical Formulation
The Ship Routing and Scheduling Problem (SRSP) addressed in this paper is described as follows:
Given a number of ships with different capacities, each one of them will serve a number of customers by, possibly, making more than one trip from a customer to another within the time horizon. A trip is portions of the route, starting and finishing at the origin, see Figure 1. The route for a specific ship is defined as the total number of all the trips this ship has made. A schedule consists of all the routes together with the servicing time of each shipment in the route. The requirements of all customers must be satisfied by the company operating the ships. Each customer imposes a delivery time window according to an arranged contract with the company. Unloading must take place within the delivery time window. If the ship arrives before the time window, it must wait until the start of the delivery time window before unloading. The objective function which searches for minimizing the overall cost, should consider all the operating expenses, such as fuel consumption, crew wages, maintenance, fixed cost of chartered ships, and other expenses.
This problem is defined formally as: N is a set of vertices (shipments), N = {0, 1, ···, n}, where 0 is the origin and n is the total number of shipments-port to be visited. There is a set of ships, V = Vc + Vch, where Vc is the total number of controlled ships belonging to the company to serve n shipments with different capacities. Vch is a fleet of chartered ships, where the company can resort to the market to charter if there are insufficient ships to deliver all shipments.
It is assumed that all chartered ships will be available at the beginning of the schedule. To address this problem, a list of all shipments is arranged and numbered in sequence according to their earliest delivery time-window.
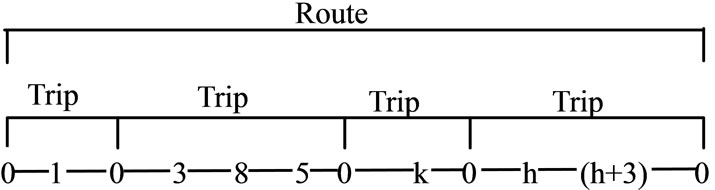
Figure 1. Illustrate the route and trip.
So, the shipment with the earliest delivery time-window will be considered as shipment number one, and so on for other shipments. The ships, on the other hand, are numbered according to time availability in origin.
To illustrate, suppose for example, that there are 10 shipments and 4 ships available. Figure 2 illustrates all possible routes to satisfy all shipments and the operating cost for each route using specified ship.
For example, ship 2 has two trips: the first trip has only one shipment for customer 2; the second trip has two shipments for customers 8 and 5.
Figure 3 illustrates the schedule for 10 shipments to be delivered by a fleet of ships including the total operating cost.
The schedule displays all the shipments and their allocated ships, where the shipments are arranged in sequence according to their earliest delivery time-window as mentioned previously. More precisely, this sequence does not imply that each shipment will be delivered according to its arrangement: For example ship number 2 (in Figure 2) delivered shipment 8 before shipment 5.
In this paper, an approximate approach method based on GA is considered. Detailed notations are given below.
Data:
V = {1, ···, m}, denotes the set of m ships to be scheduled, indexed by v, where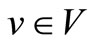 .
.
N = {0, 1, ···, n}, denotes the set of n shipments to be delivered, indexed by i, where  and 0 denotes to origin and
and 0 denotes to origin and 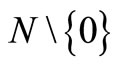 denotes shipments.
denotes shipments.
AVv denotes to the availability time of ship v at the origin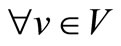 .
.
ei earliest arrival time for shipment i, .
.
li latest arrival time for shipment i,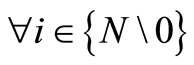 .
.
Qi shipment quantity of shipment i (tons)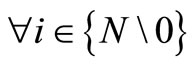 .
.
dik distance (in days) between shipment-port i and shipment-port k, where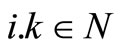 .
.
CTv capacity of ship v (tons)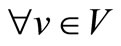 .
.
Rv Route of ship v,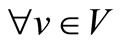 .
.
CPiv port entrance due (fee) at shipment-port i for ship
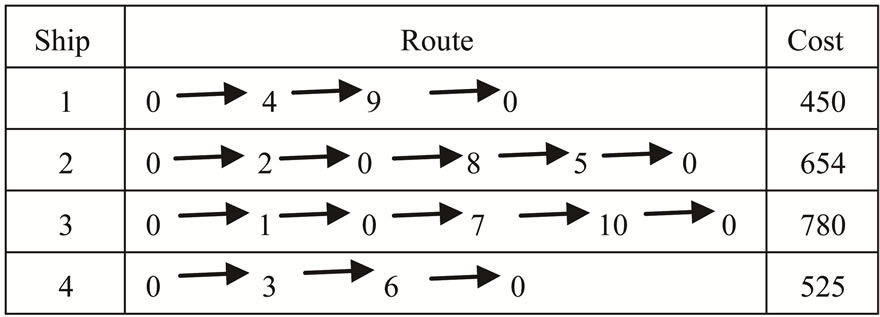
Figure 2. Illustrate the route for each ship and the cost for each route.

Figure 3. Illustrate 10 shipments are delivered by 4 ships, and the total operating cost.
v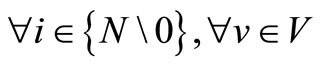 .
.
SPv sailing cost using ship v (per day)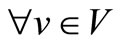 .
.
LDiv time required for loading shipment i onto ship v (days)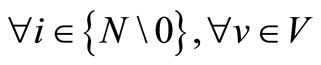 .
.
ULiv time required for unloading shipment i from ship v (days)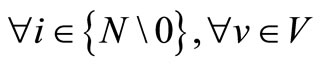 .
.
OCiv operating cost for ship v to handle shipment i, including loading and unloading costs 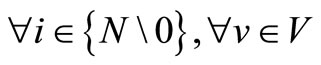 .
.
Wpv waiting cost (idle in the ocean) for ship v (per day)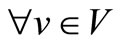 .
.
Decision Variables:
fiv actual arrival time for ship v to shipment-port i,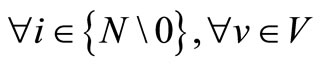 .
.
Wiv duration of waiting (idle) time for ship v until time-window of shipment-port i opens (days)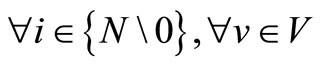 .
.
tsv total sailing using ship v,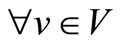 .
.

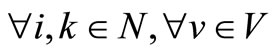 .
.

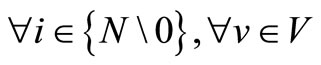 .
.
The variable of actual arriving time fiv can be computed using one of the following two equations according to ship position:
1) fiv = AVv + LDiv + d0k + wkv + ULkv + dki + wiv if ship v sailing direct from origin and loading to deliver shipment k then shipment i.
2) fiv = fkv + ULkv + dki + wiv, if ship has delivered shipment k.
If ei ≤ fiv ≤ li, where ship v arrived shipment-port i within time-window, in that case Wiv = 0. On the other hand, if fiv < ei, which means, ship v arrived the shipment-port i before earliest start time. On this time, Wiv can be computed using the following equation: Wiv = ei – (fkv + ULkv + dki).
The total sailing tsv using ship v can be computed by

The operating cost and port entrance due for ship v for the entire route can be computed by:

where the total cost TC for this problem can be counted by:

4. Problem Approach
Section 4.1 presents the approximation approach based on GA, while the exact algorithm is presented in Section 4.2.
4.1. Solving the Problem by the Genetic Algorithm
In this paper, the GA starts by generating two chromosomes (solutions) which represent the first two parents. The representation of each chromosome is an integer string of length N, where N is the number of shipments in the problem. Each gene in the chromosome is the integer number of a specific ship assigned to that original shipment. Not like other application of GAs, where usually generate a number of chromosomes which form a population. In this research, initial solutions are generated to produce two parents. Operations such as crossover and mutation are applied to parents to produce offspring (children). The new generation is considered as the new population and the procedure is repeated. Through each mating process, each chromosome will be evaluated according to the feasibility; any infeasible solution is not acceptable and must go through a repair operation to fix it. Repairing procedure will be applied after each operator (crossover or mutation). The lower fitness value will be stored and compared with other new chromosome. The process will carry on until a specified number of iterations are reached.
One of the initial parents can be obtained by using a Greedy Algorithm, while the other parent is generated randomly. The Greedy Algorithm starts by selecting the ship with the least overall cost ship. A route is then created for this ship starting from shipment number one in the list, provided that all constraints such as capacity and delivery time window are satisfied. The process can be presented as follows:
1) The insertion of shipment i in a route for ship v, does not violate the delivery time window if ei ≤ fiv ≤ li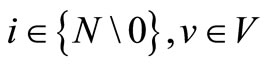 .
.
2) The insertion of shipment i in a route for ship v, does not violate the capacity of ship v if Qi ≤ CTv, .
.
The next step is to select the ship with the next lowest cost and considering the unallocated shipments in the list. This procedure will carry on until no shipment remains unallocated. For instance, a schedule of n shipments is illustrated in Figure 4.
In Figure 4, shipment 1 is served by ship 3, shipment
2 is served by ship 1, and so on until last shipment n is served by ship k.
In the rest of this research, representation of schedules will be as chromosome, for example, Figure 5 illustrates the previous schedule in Figure 4.
Note that after forming the initial chromosome (schedule), it is possible that one or more ships are not used in this schedule. These ships are referred as idle ships. These ships will be available during GA operation.
The following section explains the methodologies for solving this type of problem by using the GA method, and describes separately the characteristics of each component of the method.
4.1.1. Crossover Operator
Crossover is a genetic operator that mates two chromosomes (parents) to produce a new chromosome (offspring). Mating implies that a portion of chromosome one is swapped with another portion from chromosome two. The new chromosome may be better than both of the initial parents in case it takes the best characteristics from each one of the parents. Three different types of Crossover can be reported in the literature: Single point (1-point), 2-point, and 4-point. Since the results of using 1-point crossover operator were modest comparing with the two other types, the results will not be discussed. In the 2-point crossover two points in chromosome are chosen randomly, while in the 4-point four points in chromosome are chosen randomly as well. Figure 6 illustrates 2-point and 4-point crossover.
In 2-point operator, swapped every genes value between the two chosen points (portion) with the genes value between the two chosen points in the opposite parent, which generate two offspring. Figure 7 illustrates 2-point operator.
In the 4-point crossover, two portions are considered in each parent. Therefore every gene belonging to portion one in the first parent will be swapped with a gene from the portion one in the second parent. The same idea applies to portion two. This operation will generate two offspring. Figure 8 illustrates 4-point operator.
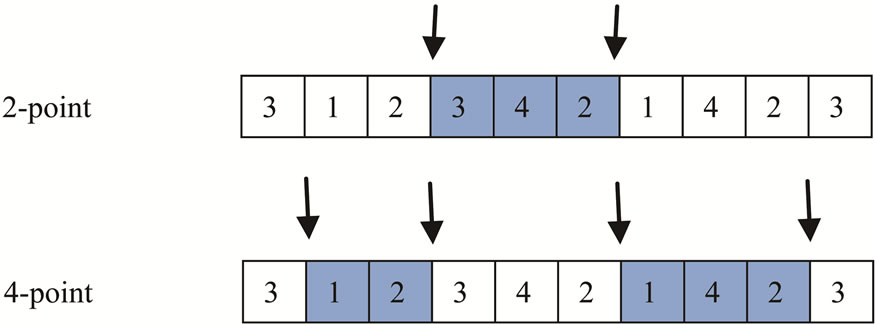
Figure 6. 2-point and 4-point crossover operators.
The procedure of crossover is performed by swapping the two selected portions as illustrated in Figure 9. We adapted the 2-point crossover operator as example.
The procedure of crossover is performed as following:
Insertion and backtracking procedure: we start inserting the selected shipments (genes 4, 5, and 6) in the exchange ships and determine their position in ship’s route. For instance, the insert trail of shipment 4 in the route of ship 1 for offspring1 will be as illustrated in Figure 10.
The criterion adopted in the insertion is as follows: For example, if shipment 4 is going to be inserted between shipment 2 and 7 as in Figure 11, the following conditions must be satisfied:
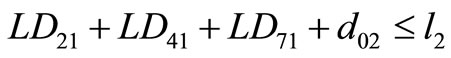 (1)
(1)
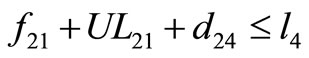 (2)
(2)
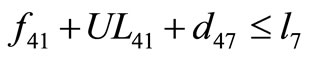 (3)
(3)
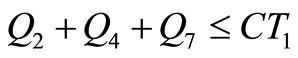 (4)
(4)
The insertion may shift the positions for some original shipments in the ship route as illustrated in Figure 11 where the shipment 7 is moved one step forward, or, due to some limitations (such as ship capacity), some shipments are possibly transferred to next the trip as shown in Figure 12 where shipment 7 is transferred to next trip.
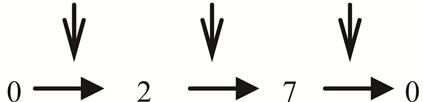
Figure 10. Potential insert trial places for shipment 4 in ship 1.
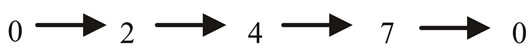
Figure 11. The effect of insertion on shifting the position of a shipment on a trip.

Figure 12. The effect of insertion on transferring the shipment to next trip.
Insert trail proposed in this research will increase the investigation in search area and give good chance to reach good solution by utilizing waiting time, exploit ship’s capacity.
Backtracking procedure will be applied that ensures that the ship capacity and the delivery-time are not violated after insertion. This process is applied for the entire route starting from the first shipment until the last one in the route after every insertion, to check the feasibility, where all constraints are satisfied.
In general, the backtracking is carried on to satisfy the two conditions:
1) The trail does not violate any constraints such as ship capacity CTv or delivery time-window of shipment i.
2) The trail does not violate any constraints for the original shipments in the route of ship v (Rv).
If the insertion succeeds, then a feasible solution is generated. The next chosen shipment will go through the same insertion and backtracking mentioned previously, until no shipment is leftover.
Otherwise, if the insertion procedure failed for all potential places for this specific shipment, then no feasible solution is generated and this gene will be left empty; that is this is an invalid offspring and needs to go through a repairing procedure.
Repairing. This applies in case of generating infeasible solution. The key idea of repairing is to select a ship with the lowest overall cost and try to insert it in the leftover shipment so that the two conditions (ship capacity and delivery time window) are fulfilled. This procedure is repeated with the other ship having the second lowest cost until no empty gene in the chromosome is left.
4.1.2. Mutation Operator
The key idea of the mutation operator is to consider the chromosomes generated by the crossover and swap one gene selected from chromosome 1 with another gene selected from chromosome 2 as illustrated in Figure 13. The selection of each gene is done randomly. Unlike the crossover operator that concentrates on local optima are, the mutation may expand the search to a wider area and allows to divert the search to outside the area defined by the crossover. This swapping will result in a new chromosome. To test whether this is feasible or not, the insertion, backtracking, and repairing procedure are applied as explained in the previous section.
The procedure diagram of the proposed GA is shown in Figure 14.
4.2. Exact Algorithm
The approach adopted to solve this type of problem is based on the Set Partitioning Problem (SPP). The major advantages of SPP models are that cost can be easily incorporated when generating all feasible schedules. The SPP model involves generating candidate feasible schedules and can be solved by use of a heuristic method or by optimization depending on the desired solution quality and the time available for solution. SPP is a widely used model for solving routing and scheduling problems, Christiansen et al. [3] reported that 40% of the reviewed papers use the SPP models or a variant. This research adapted SPP for exact solution, where candidate feasible schedules are generated.
In this section, notations and formulation for solving SRSP are presented, while the full description of generation of the candidate schedules will be presented in the
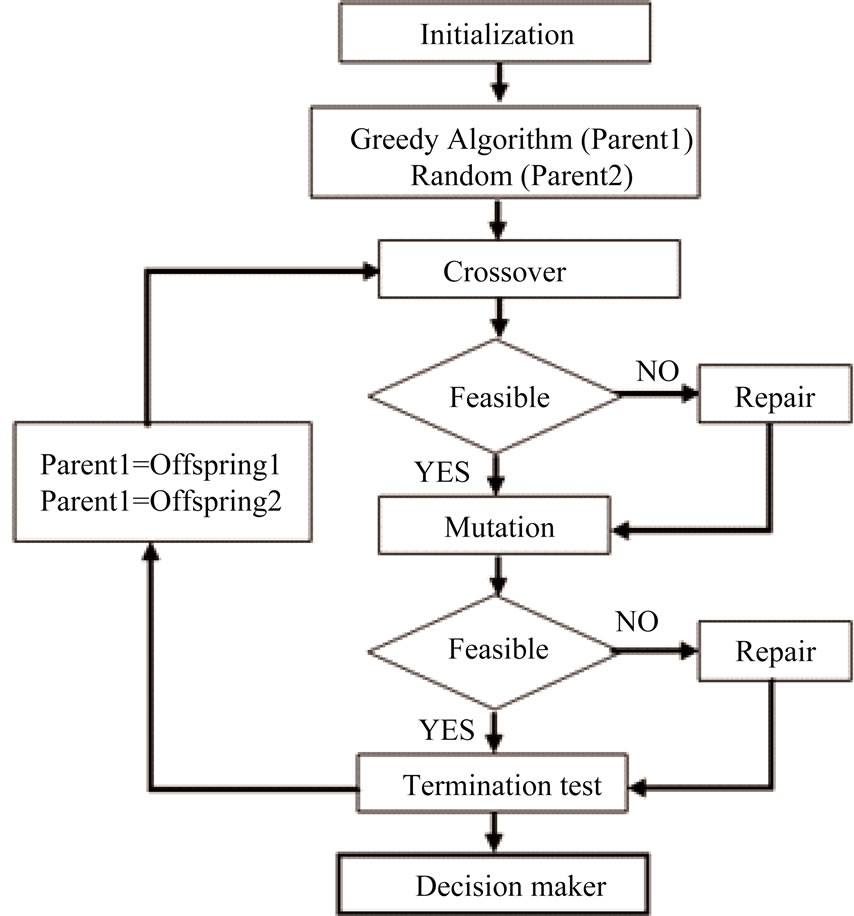
Figure 14. Operation of genetic algorithm.
following section.
Sv denotes to a set of candidate schedules are available for ship v, and j indexed to specific schedule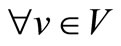 .
.
Cvj denotes to the cost for using schedule j for ship v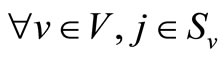 .
.

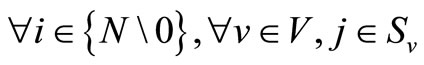 .
.
Decision variable

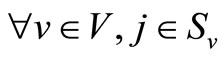 .
.
The following is SPP based formulation for solving SRSP:
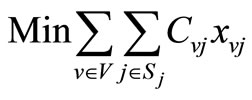 (5)
(5)
Subject to
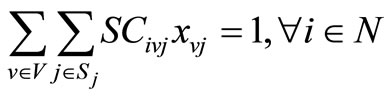 (6)
(6)
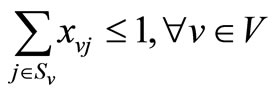 (7)
(7)
 (8)
(8)
The objective function (5) represents overall cost. Constraints (6) ensure that all shipments have been delivered either by controlled ship or spot chartered ship. Constraints (7) ensure that each ship has used at most once.
The following section will explain the method of generating all possible candidate schedules SCivj.
4.2.1. Generation of the Candidate Schedules
Candidate schedule generation uses a procedure that generates a set of feasible candidate schedules, each of which corresponds to a variable in the SPP model. Each individual candidate schedule has a route for a specific ship containing one or more shipments. A number of candidate schedules for a specific ship are represented by a subset. The union for all subsets (for the set of all ships in the fleet) forms a set of candidate schedules The generation of schedules is implemented in a systematic way by expanding an existing schedule by inserting a new shipment. Since the route in the schedule consists of origin and shipment nodes, there are at least 3 nodes in each route, where the first and the last nodes represent the origin. Before continuing to explain the method of generating candidate feasible schedules, it is necessary to illustrate the test of feasibility for each generated schedule.
Feasibility tests for each generated schedule will be implemented by considering each ship capacity or availability time at origin, as follows:
1) To ensure that each ship arrives not after the latest required time-window, the following test is necessary
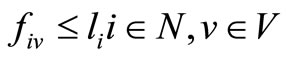 (9)
(9)
2) To ensure a ship has sufficient capacity to handle a specific shipment, it is necessary to add the following test:
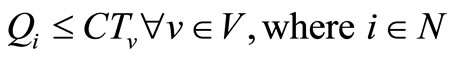 (10)
(10)
These two tests will apply for each generated schedule to ensure that SPP will consider only feasible schedules.
To simplify this procedure, consider an example with three shipments and one ship. If all constraints are relaxed, then Table 2 illustrates all the candidate schedules that can be generated:
5. Comparison between SPP Approach and GA Approach
5.1. Description of the Test Problems
The major objective of the computational experiment reported here is to evaluate the performance of the proposed GA designed model in terms of the quality of the solutions and the computing time. This evaluation can be implemented by comparing the results of the two approaches: the exact method using SPP and the GA designed model.
Since there were obstacles in obtaining some information related to Kuwait Petroleum Company (KPC), due to commercial confidentiality, random data are generated using distributions close to the reality. Data involved in SRSP can be presented as follows:
1) Ship details (Time availability at origin, capacity, sailing expenses, and waiting in the sea expenses).
2) Distance between shipment-ports (include origin).
3) Shipment details (delivery time-window (start and close) and quantity).
4) Loading & unloading duration, and the cost of ship.
5) Port fee due for each ship.
The user can enter a specific data that defines a particular problem instance of SRSP by using a designed interface. The component of the interface consists of all data involved in SRSP presented previously.

Table 2. All candidate feasible schedules.
Six cases are examined with different number of shipments and ships. Twenty five randomly generated instances for each of these problem sizes were used. Ship time availability, ship capacity, shipment-port duration, shipment amount, and shipment-port delivery time window are all generated from a Uniform distribution, where time-horizon is equal to 150 days for each case. Table 3 presents the features for each case.
5.2. Numerical Results
GA method was coded and implemented using Visual Basic 6, running on Intel Core 2 Duo, 2.50 GHz CPU.
The second approach is an exact method based on the Set Partitioning Problem SPP. The implementation language Visual Basic 6 was used to generate all candidate feasible schedules, while the commercial optimization solver CPLEX-11 was used for optimality.
In this section, experiment results for approximate and exact models are presented. First, experiment results for approximate models with different neighborhood size (NBS) are given. Table 4 (in the next page) displays the computational results for six cases, where, twenty five different problem instances were generated (150 different problems are the total), and shows the computational results when varying the value of the neighborhood size (NBS) for the crossover operator. Searching terminates after reaching 60,000 iterations. For all cases, the average of the mean of the overall operating cost (objective function) is presented. Meantime, the average of the gap between the best solution and the current solution are presented in percentage to measure the quality of the solution, where zero indicates the best solution of this specific case.
In addition, last column (Average Gap %) evaluate the best gap among all cases, where the smallest gap is the best. In case 1, the best solution is obtained when NBS is equal to 10% using 4-Opt. For cases 2 and 4, NBS is equal to 40% using 4-Opt are produced the best solutions, while in cases 3 and 6, NBS is equal to 30% using 2-Opt are presented the best solutions. Lastly, for case 5, the best solution when NBS is equal to 40% using 2-Opt. In general, the solutions were very close by using different NBS, where the large gap is equal to 3.37% in case 1 with NBS equal to 40% using 4-Opt. Meantime, the solution is slightly better when adapted NBS equal to 30% using 2-Opt, where the average gap is equal to 0.39%. Finally, the computing time is increased proportionately when the NBS increased for all experiments.
The generation of candidates feasible schedules and finding the solution by set partitioning problem (SPP) required more CPU-time. Table 5 illustrates the computing time required for generating candidates feasible schedules and finding the solution by SPP for only cases 1, 2, and 3, where the CPU-time is increased exponentially. Table 5 shows the increase of the number of candidate schedules generated, and computing time corresponding to the increase of the problem size. The computational experience indicates that CPU-time required to generate the candidates feasible schedules profoundly depends on many parameters such as; number of shipments, time horizon, delivery time-window width, distance between shipment-ports, number of ships involved, etc. This pointed to that more time is required to solve medium and large-scale problems, and necessitates to resort to another heuristic methods capable to of generating solution close to optimality, such as GA method proposed in this research.
Table 6 presents the computational comparison results for approximation approach (GA) and exact approach (SPP) for six cases, 150 different problems are generated. The results for all cases represent schedule generations, applying Set Partitioning model, and applying GA model. Number of shipments and ships as illustrated in Table 3.

Table 3. Problem features to evaluate problem size.

Table 5. Details of number of schedules generated for the first three cases.
Q: Quality value (overall operating cost) of the objective function. T: Computing time. Gap (%): Gap in percentage between current quality value and best quality value. (Current quality value-Best quality/Best quality) × 100.


Table 6. SPP and GA computational results.
For cases 1 and 2, the problems were solved by generating all feasible schedules (Rmax = ∞), thus ensuring optimal solution. This could not be implemented for the other cases (3, 4, 5, and 6) due to memory problems, where it is clear in case 3 that only 5 instances out of 25 problems were solved, as illustrated in Table 4. The number of candidate schedules for cases 3, 4, 5, and 6 has a limit set at 900,000, where, a subset of candidate schedules are selected.
According to Table 5 the generation of candidate feasible schedules of case one requires CPU-time more than the time required to obtain the solution of the set partitioning problem. This is due to the exponential computational time, which does not occur for the other cases.
For the medium and large scale problems, the solutions obtained by SPP lose the property of optimality since only a subset of all feasible schedules can be included in the model. In Table 4, where for cases three to six the gap is 26.2%, 21.8%, 22%, and 16.1% respectively. This is due to the total number of the subset of candidate feasible schedules generated for each case, where in case three the number is large (up to 50000 schedules for each ship), while it gets smaller for the next cases (the candidate feasible schedules for case six do not exceed 20000).
Further, GA returns better solutions in term of solution quality compared to Tabu Search (TS), Alhamad [8], where the computing time for the latter is. However, in GA computing time is slightly large.
The results given in Table 6 show that the gap between the solutions obtained by GA and SPP is slightly large. In addition, more time is needed to solve medium and large scale problems by the SPP because the computing time increases exponentially with the problem size. However, the GA generates good solutions for such types of problems more quickly. The performance of GA is more predicted in term of computing time.
An attempt to solve problems involving more than 100 shipments such as 125 shipments using the SPP was carried out, but, infeasible solutions were obtained. This happened in some instances in case six, where four out of twenty five cases, generated infeasible solutions.
Many factors influence the number of candidate schedules. These include time horizon, the delivery time window and the ship capacities.
Therefore, user can use SPP for small scale problems where optimal solution is guaranteed, while for medium and large scale problems, user can refer to GA to produce good solutions.
6. Conclusions
This paper describes a new optimisation based approach for SRSP. Two computational approaches to handle SRSP are considered. The first is an approximate method based on GA and the second approach is an optimisation approach based on the SPP. For the optimisation approach, a number of candidate feasible schedules are generated, each of which corresponds to a variable in the SPP model.
The major objective of the computational experiment was to evaluate the performance of the proposed GA designed model in terms of the quality of the solutions and the computing time. This evaluation was achieved by comparing the results of the two approaches: the exact method using SPP and the GA designed model.
Computational results also indicate that the optimization approach can solve some moderate size problems by using a method to generate a subset of feasible schedules, which is considered very close to optimal solution. On the other hand, a very large problem will be difficult to be solved due to out of memory, where it recommends to resort to GA for solving them. Meantime, computational results indicate that GA in term of the quality of the solutions is slightly better than other published work using Tabu Search method.
Experiment results presented for the GA approach indicate that when the number of iterations is large, better solution may obtain. However, some users prefer reasonable solution in less time consumption. Therefore, for large scale problems, the user can reduce the total number of iterations, if time is matter.
Further works can be done using soft delivery timewindow. This means that the delivery time-window can be violated, however, penalties is impose. Most customers impose a delivery time-widow for their shipments. Any violation of delivering is considered unacceptable, where some of those customers impose penalties for any violations. Therefore, large ship can be loaded up to its capacity even the delivery can be violated, if this approach reduces the overall cost. Meanwhile, customer considers delivering outside delivery time-window is unacceptable, will be satisfied by increase the penalty to enormous number.
7. Acknowledgements
The authors would like to express their gratitude to Dr. M. K. El-Daou for the valuable comments, help, support, and important hints he provided to this paper.