On a Theme by Heckscher-Ohlin: A Diffusion Model for Spatial Dynamics in Factor Prices ()
This paper presents an analytical study of the cross-sectional distribution of factor prices over time and across space. A methodology is proposed, which offers a novel representation for the Heckscher-Ohlin model and its key implications, including the Factor price equalization, the Stolper-Samuelson and the Rybczynski theorems. A driftdiffusion model is proposed to describe the dynamic process governing the fluctuations around the equilibrium distribution of factor price. The model is mechanical and descriptive in nature, and illustrates that the growth distribution of factor price can be generated by a single stochastic process that builds upon the theory of diffusion processes.
The dynamics of the proposed model rely on two opposing flows: 1) a factor equalization process which is meant to concentrate the distribution, and 2) a counteracting diffusion process which is meant to describe noise thus flattening the distribution. One of the parameters entering into diffusion is motivated by random shocks. It is hypothesized that these flows follow simple evolutionary laws that can be described with five parameters— parameters that can be estimated from historical data with some accuracy.
An empirical application of the proposed model, to the evolution of the distribution of incomes for 186 countries, recorded from 1993 up to 2007, illustrates the applicability of the proposed method for studying income distribution dynamics, and suggests that diffusion may be a preferable technique for the analysis of spatial dynamics in factor prices.
The question posed by this paper is an original one. While much attention has been given in the literature to the explanation of the shape of income distribution at a given point in time by reference to steady state arguments [1-4], the dynamics in question have been relatively ignored. The main objective of this paper is to contribute to our understanding of some determinants of the dynamic process governing the distribution of income, and build up a tractable structure for its analysis. This is achieved by deriving both the steady state distribution as well as the dynamic behavior of the model. Steady state analysis is used here to study the long run properties of the proposed dynamic model. The aim of our method however, is to understand how information on the time evolution of income distribution over an extended period of time can be used to make inferences about an underlying process. It is shown that interesting issues arise when one considers how income distributions evolve over time, rather than simply attending to equilibrium implications of processes, example with respect to the degree of flexibility in labor markets. To that end, results for 1) the final equilibrium distribution as well as 2) the extent and speed of adjustment to this said equilibrium are presented.
2. Introduction and Theoretical Framework
The Heckscher-Ohlin model (H-O) is a general equilibrium model of international trade, first developed by Eli Heckscher and Bertil Ohlin. The foundations of the model rest on David Ricardo’s theory of comparative advantage. The model predicts patterns of trade motivated by factor endowments; countries will export products that utilize their abundant and cheap factor(s) of production and import products that utilize the countries’ scarce factor(s).
The elegance of the general equilibrium framework constructed by Heckscher-Ohlin and the predictions for the pattern of trade seduced the economics profession. Key implications of the basic neoclassical general equilibrium framework were derived, including the Factor price equalization theorem, which states that free trade in commodities will equalize the relative prices for two identical factors of production. Another implication relates to the relationship between goods prices and factor prices: Stolper-Samuelson theoren, which states that under some economic assumptions (constant returns, perfect competition), a rise in the relative price of a good will lead to a rise in the return to that factor which is used most intensively in the production of the good, and conversely, to a fall in the return to the other factor. Regardless of international factor mobility, factor prices will tend to equalize across countries that do not differ in technology. A third implication of the framework relates to the relationship between factor supplies and goods production with the Rybczynski theorem.
Heckscher and Ohlin lived in one of the most important periods in the field of international trade. The authors were motivated by the commodity-price equalization trends in the late nineteenth century. What occurred in the late nineteenth century, the authors observed, was the kind of exogenous relative price shock which is supposed to set factor price equalization in motion. According to the theorem, the invasion of grains should have raised the wage-rental ratio in the Old World while lowering it in the New World, ceteris paribus. In Ohlin’s words, “trade increased the price of land in Australia and lowered it in Europe, while tending to keep wages down in Australia and up in Europe” [5].
Responding to regional wage differentials, labor (capital) migrates from low-wage (high-wage) to high-wage (low-wage) states/regions. As the capital/labor ratio rises in the low-wage states, growth of wages accelerates. Mallick (1993) describes this process as convergence: wages in the initially poor states converge towards those in the initially rich states. Richer countries start out with higher capital-to-labor ratios, but tend to experience diminishing returns to capital faster, leading to a slower growth than in the poorer nations. This process is reinforced as the poorer nations assimilate technology of the richer nations [6].
The Hecksher-Ohlin theory remains a cornerstone of international trade theory in the Economics literature. Given the importance of understanding the validity of this theory not only as basis for international trade, but also for understanding the impact of trade on factor prices as well as their distribution, key theoretical advances have enriched the theory. In particular, rigorous statistical analysis has sought to investigate the empirical validity of the H-O theory as an illustration of international trade patterns.
The Leontief’s paradox [7] claimed that the factor price equalization and the Heckscher-Ohlin theorems appear to be at variance with observed international differences in factor prices and international trade in factor services; trade pattern of the United States did not seem to fit the prediction of the H-O theory. Using 1947 U.S. data, Leontief showed that the capital/labor ratio for U.S. imports exceeded the capital/labor ratio for U.S. exports. A large debate ensued. Leamer [8] has ultimately resolved this puzzle by illustrating that Leontief’s method of identifying the ratio of the factor content of exports to that of imports may not identify a country’s abundant factor. Leamer has instead suggested that a country will allocate resources between industries to maximize the total value of outputs [9,10].
Departures from the Factor price Equalization hypothesis and the H-O theorem have been examined theoretically and empirically by Trefler [11], who has examined a modification of the H-O model that allows for factor-augmenting international productivity differences. Trefler illustrates that such an adjustment to the H-O theorem may explain much of the factor content of trade and the variation in factor prices across nations. In Trefler’s study, international productivity differences are consistent with factor price differences observed across nations. Trefler suggests that there are two major sources of the mysteries: country-specific productivity differences, and Armington bias in consumption toward home goods.
In parallel, a fierce debate over what is termed the convergence-divergence hypothesis has enriched the economics literature with extensive attempts to document cross-country patterns in incomes [12-22]. Some studies cite evidence for convergence of cross-country incomes, which implies that cross-section dispersion in incomes diminishes over time. Some others suggest that while there are pockets of convergence, the data overall show a tendency for divergence of cross-country incomes. Yet other studies cite evidence of conditional convergence. Some of these studies suggest that this conditional convergence happens at approximately the same rate over different time periods and across different cross-sectional samples.
The neoclassical growth model a La Solow [23] predicts that countries reach different steady states. It has been argued that much of the cross-country differences in income per capita can be traced to differing determinants of the steady state in the growth model: accumulation of human and physical capital and population growth. Thus, the neoclassical growth model does not predict convergence; it predicts only that income per capita in a given country converges to that country’s steady-state value. In other words, the Solow model predicts convergence only after controlling for the determinants of the steady state, a phenomenon that might be called conditional convergence. In addition, the Solow model makes quantitative predictions about the speed of convergence to steady state [2].
Without getting into the debate over the extent of convergence/divergence in factor prices, the present paper explores a different representation for the dynamics in the evolving distributions and illustrates that the growth distribution of incomes can be generated by a single stochastic process in which the logarithm of the quantity in question follows a Brownian motion. We develop a model, built upon the theory of diffusion processes, and propose a methodology for examining the dynamics of cross-sectional distribution of income. Our picture of world development is one where some economic forces push in the direction of convergence whilst other forces are divergent. Globalisation typically reinforces the convergent trend through the flow of capital towards capital poor economies, through trade-induced factor price equalizations and through international trade. We postulate a counteracting force which tends to collapse the cross-section distributions. Consistent with this observation, a model is proposed for fluctuations over time in the density of cross-sectional distribution of incomes. The methodology is a more transparent way to measure the importance of convergence/divergence and fluctuations, which avoids the complications associated with dynamic inference which taint tests derived from calculating cross-section regressions of measured growth on initial levels [3,24].
Our study is motivated by the observation that the distribution of incomes across regions varies as a function of time. This suggests that there exists an equilibrium distribution of incomes with a certain mean and variance, towards which the ensemble of states considered tend to converge, and there is a speed of convergence towards this said equilibrium distribution. In order to quantify this process, the present paper presents an analytical study of the evolution of cross-sectional distribution of income. It is hypothesized that the growth distribution of incomes can be generated by a single stochastic model that builds upon the theory of diffusion processes. The proposed model describes the density of cross-sectional distribution of incomes and models the time evolution towards the equilibrium distribution1.
The dynamics of the proposed model rely on two opposing flows: 1) a factor equalization process which is meant to concentrate the distribution, and 2) a counteracting diffusion process which is meant to describe noise and flattens the distribution out. One of the parameters entering into diffusion is motivated by random shocks. It is hypothesized that these flows follow simple evolutionary laws that can be described with five parameters— parameters that can be estimated from historical data with some accuracy.
An empirical application of the proposed model, to the evolution of the distribution incomes for 186 countries, recorded from 1993 up to 2007 illustrates the applicability of the proposed method, and suggests that diffusion may be a preferable technique for the analysis of income dynamics. Neoclassical models do not account for dispersion. Our model incorporates both drift and diffusion. Our findings have interesting implications for theories of growth and the business cycle and suggests that diffusion may be a preferable technique for analyzing the dynamics of factor prices across time and space.
The question posed by this paper is an original one. While much attention has been given in the literature to the explanation of the shape of world income distribution at a given point in time by reference to steady state arguments [1-4], the dynamics in question have been relatively ignored. The main objective of this paper is to contribute to our understanding of some determinants of the dynamic process governing the distribution of income, and to build up a tractable structure for its analysis. This is achieved by deriving both the steady state distribution as well as the dynamic behavior of the model. Steady state analysis will be used here to study the long run properties of the proposed dynamic model. We use it here most importantly however, to understand how information on the shape and evolution over time of income distribution can be used to make inferences about an underlying process. It is shown that interesting issues arise when one considers how income distributions evolve over time, rather than simply attending to equilibrium implications of processes, example with respect to the degree of flexibility in labor markets. The results illustrate the usefulness of the method in analyzing both the extent and speed of convergence/divergence in income distribution, and results are presented for 1) the final equilibrium distribution as well as 2) the speed of adjustment or rate of convergence to this said equilibrium.
The paper is organized as follows: Section 3 develops and provides an analysis of the model. Section 4 reports some empirical results. Section 5 presents concluding remarks.
3. The Model
Consider a region consisting of a constant number of states with different levels of income. Some states are richer than others. The set of incomes forms a distribution which evolves over time. As a result of differentials in wage rates across countries within regions, labor migrates from low-wage to high-wage countries. Likewise, capital migrates from high-wage to lower-wage countries within the region. As the capital/labor ratio falls in the high-wage countries, wage growth slows down. As the capital/labor ratio rises in the low-wage countries, growth of wages accelerates. Wages in the initially poor countries converge towards those in the initially rich ones. Richer countries start out with higher capital-tolabor ratios, but see diminishing returns to capital set in faster. As a consequence, they grow slower than the poorer countries. This process is reinforced by transfer of technology and knowledge from richer to poorer countries2 [6,25].
A counteracting force exists, in the form of economic, political and institutional blockages and faster population growth, which causes bottlenecks in diffusion of knowledge and ideas and thus creates divergence in the system. Moreover, mobility of labor and capital may se impeded by the presence of consumption and production externalities. Evidence reveals that while workers may migrate in response to wage differentials, firms generally do not. Migration of firms to low-wage areas is therefore limited, due to factors such as increasing fiscal burdens, crises in the poorer states, and relative inelasticity of housing stock [6].
More precisely, for the drift spread, it is assumed that there exists some equilibrium distribution of real wages with a certain mean and variance, towards which the ensemble of countries within a region tend; i.e., a flux towards the equilibrium distribution. Drift is driven by diminishing returns to capital, which in turn leads to factor price equalization. Though the flow of capital and labor play a role, it is the flow of ideas that is the main force driving drift. Diffusion is driven by random shocks. Late-comers grow faster than early-comers. It is assumed that income levels spread from high density towards lower density levels. This happens as a result of economic integration or openness in the sense of Sachs and Warner [28,29]. The more open grow, the less open decline, but in any case there is a spreading away from the initial income3. The speed of spreading parameter is proportional to mobility of factors of production. Consistent with Barro et al. and Lucas [14,25], convergence is a result of adjustment of capital-labor ratios to common steady-state levels, starting from different initial values4.
It is assumed that there exists an equilibrium distribution of incomes with a certain unknown mean and variance, determined by the tension between counteracting forces of convergence (migration of labor and flow of ideas) and divergence (bottlenecks to flow of labor, capital and ideas). At any moment in time, a discrepancy exists between the current actual wage distribution and the equilibrium distribution and states find themselves in a dynamic adjustment process toward such an equilibrium. The adjustment process depends on speed of diffusion of factors of production, and the evolution of the income distribution reflects the convergence towards this equilibrium.
Consider
 (1)
(1)
where f denotes the probability density of incomes and qc measures the portion of the function f transported by the drift velocity. u denotes the mean of the distribution at equilibrium. s measures some relevant aspect of income in logarithms, and λ denotes the velocity at which income approaches its equilibrium level, which depends on the speed with which diminishing returns set in. If diminishing returns to capital set in more quickly, a more rapid rate of convergence is implied. Other elements of an open economy-the mobility of labor and technology-tend to speed up the rate of convergence.
For the diffusion spread, although an equilibrium distribution exists, this equilibrium is assumed uncertain from the point of view of the observer. Random effects therefore tend to cause a spread of income from high density towards lower density. This happens as a result of learning and the phenomenon of catch up, and is consistent with findings that illustrate the early leaders in industrial revolution like the UK and the Netherlands needed over 50 years for income to double from $2000 to $4000, but countries that only reached $2000 after 1950 needed 10 - 20 years [25]. Thus there is a spreading away from the initial income. This learning process generates randomness in the system [30]. The speed of spreading parameter is interpreted as depending on learning speed which is proportional to the mobility of factors of production.
The simplest choice is Fick’s law (Okubo 1980):
 (2)
(2)
where f measures density and s measures some relevant aspect of income in logarithms. ε > 0 is a constant diffusion parameter. Thus we have
 (3)
(3)
Noise in this model is generated by diffusion of knowledge and learning [31-34], and limited by the presence of obstacles in the form of trade barriers. Due to counteracting forces of drift and diffusion, a discrepancy exists at all times, between the current actual distribution and the equilibrium distribution. The selection process is always in a transient phase, groping toward its temporary equilibrium, and countries find themselves in a dynamic adjustment towards such an equilibrium. The adjustment process or speed of spreading parameter depends on learning speed, and the evolution of the distribution reflects convergence towards this equilibrium5. Our picture of world development is thus one where convergence is counterbalanced by divergence. Convergence in the context of our model would mean collapsing of the cross-section distribution. Divergence would mean that the cross-section distribution is not collapsing, but replicates itself because for example it happens to be the stationary distribution for many independent and identically-distributed country incomes. The model allows for the cross-sectional distribution to converge and ongoing disturbances provide a force in the opposite direction. The effect from the drift parameter which tends to reduce dispersion, is offset by random shocks, which tend to increase dispersion. λ is the speed with which incomes approach steady state values, which depends on the speed with which diminishing returns set in, and on the mobility of factors of production. In our model, the more rapidly diminishing returns set in, the more rapid the rate of convergence.
3.1. Analysis of the Model
In order to describe the time-behavior of the proposed model, the model is solved for its analytic solution f(s, t), describing the evolution of the distribution through time. We impose the following initial conditions in time and boundary conditions with respect to s

on , where N is the normalization constant.
, where N is the normalization constant.
The expression representing the time-development of the distribution is:

where 

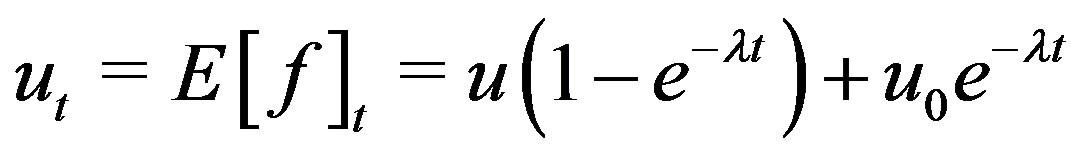

u0 represents the initial mean of the distribution and  represents the initial variance of the distribution.
represents the initial variance of the distribution.
4. Empirical Application
4.1. Data and Descriptive Statistics
The empirical analysis uses The Penn World Table purchasing power parity and national income accounts6 converted to international prices for 186 countries, recorded from 1993 up to 2007. These years were selected from Penn World Tables for analysis because it is only on these years where all countries have data simultaneously. Figure 1 shows the evolution of the distribution of income from 1993 up to 2007, and Table 1 shows the descriptive of income from 1993 to 2007. It must be noted that data points that are graphed are based on the average rate per year. It can be seen from the graph that there is a steady increase in national income CGDP throughout the selected years.

Table 1. Descriptive of income from 1993 to 2007.

Figure 1. Evolution of CGDP from 1993 to 2007.
4.2. Method of Estimation
A second order partial differential equation model has been proposed to express the dynamics of income distribution. The model has five parameters: u0, u, ε,  , and λ. u0 denotes the initial mean of the distribution, and u denotes where the initial mean is heading. σ0 is the standard deviation at time zero, ε represents the diffusion parameter, and λ determines the rate of convergence.
, and λ. u0 denotes the initial mean of the distribution, and u denotes where the initial mean is heading. σ0 is the standard deviation at time zero, ε represents the diffusion parameter, and λ determines the rate of convergence.
The expectation of our distribution is the first moment, expressed by:

Moreover, using the expression for the second moment of the distribution, the variance of the distribution , can be expressed by:
, can be expressed by:

To examine the behavior of f as t → ∞, one observes that f(s, t) → f∞(s) as t → ∞, where

and that . Moreover, the diffusive limiti.e., the limit as t → ∞ of the variance is7:
. Moreover, the diffusive limiti.e., the limit as t → ∞ of the variance is7:
 .
.
The model has been applied to the log income distribution of the population as a function of time.
4.3. Estimation Results and Model Checks
Tables 2 reports estimates for the five model parameters u0, u, ε,  , and λ, along with the standard errors and t-values.
, and λ, along with the standard errors and t-values.
It can be seen from this table that the parameter estimates conform to the real data that are presented in the descriptive analysis section above. To ascertain, one could look on the actual vs. predicted time plot that can be generated from the real data and from the estimated data. Figure 2 graphically illustrate the evolution of the distribution of CGDP (log-normals) over time, superimposed on histograms which describe the time evolution of the distribution of the CGDP in the data (for selected years, i.e., 1993, 2000, and 2007). The solid curves in these figures illustrate the distribution of CGDP as predicted by the model, and the dotted curves illustrate the distribution of the CGDP in the data.

Figure 2. Actual vs. predicted graphs for distribution of CGDP (for years 1993, 2000, 2007).
The following observations can be made concerning our results:
1) The mean of the income distribution is clearly evolving, corresponding to our theoretical predictions.
2) The variance of the income distribution is likewise evolving, corresponding to our theoretical predictions.
3) The value for the drift parameter λ, which measures the velocity at which economies approach equilibrium distribution is positive as expected.
4) The value for the diffusion parameter ε is small and positive as expected.
5) The diffusive limit, i.e., the limit as t → ∞ of the variance is: . The results predict that if we start with a normal distribution and let the model drive the distribution, the distribution variance will tend toward a constant
. The results predict that if we start with a normal distribution and let the model drive the distribution, the distribution variance will tend toward a constant  and concentrated around a mean u.
and concentrated around a mean u.
5. Final Remarks
This paper presents an analytical study of the equilibrium distribution of factor prices over time and across space. A methodology is proposed, which offers a novel representation for the Heckscher-Ohlin model and its key implications, including the Factor price equalization, the Stolper-Samuelson, and the Rybczynski theorems. A driftdiffusion model is proposed to describe the dynamic process governing the fluctuations around the cross-sectional distribution of incomes. The models is mechanical and descriptive in nature, and illustrates that the growth distribution of incomes can be generated by a single stochastic process that builds upon the theory of diffusion processes.
The dynamics of the proposed model rely on two opposing flows: 1) a factor equalization process which is meant to concentrate the distribution, and 2) a counteracting diffusion process which is meant to describe noise and flattens the distribution out. One of the parameters entering into diffusion is motivated by random shocks. It is hypothesized that these flows follow simple evolutionary laws that can be described with five parameters— parameters that can be estimated from historical data with some accuracy.
An empirical application of the proposed model, to the evolution of the distribution of incomes for 186 countries, recorded from 1993 up to 2007 illustrates the applicability of the proposed method for studying income distribution dynamics, and suggests that diffusion may be a preferable technique for the analysis of factor prices across time and space. Our findings have interesting implications for theories of growth and the business cycle. The study is in the spirit of probabilistic models of Krugman [35] who studies city sizes, and Axtell [36] and Hashemi [32,37] who study firm sizes, and Hashemi [38-40] who studies income and unemployment. Our suggestion is that these models could provide interesting insights if applied to the dynamics in the distribution of factor prices.
NOTES
2In general, globalization is typically assumed to favor factor-price equalization and the resulting convergent trend, through international trade, international migration, and the flow of capital and technology from capital rich to capital poor economies. Migration has been a very important factor towards equalization historically. However, as income gaps widened, freedom of migration has become limited by richer countries. As Lucas [25] suggests, what is left is flow of ideas which are linked to the economic interactions involved in trade.
3Sachs and Warner report a strong convergence in per capita GDP amongst the group of countries classified as open, but no convergence amongst the closed economies. The average growth premium for opening an economy is estimated not to be insignificant—2.5 percentage points on annual growth [26-29].
4As empirically illustrated by Lucas and others, the early leaders in industrialization like the United Kingdom and the Netherlands, needed over 50 years for income to double from $2000 to $4000. Countries that only reached $2000 after 1950 needed 10 to 20 years [25].
5The model is based on a drift-diffusion continuous process obtained from an Ornstein-Uhlenbeck one. The partial differential equation in this paper can also be regarded as the expectation of a classical linear stochastic differential equation. The equation in (14) is associated with the linear stochastic differential equation 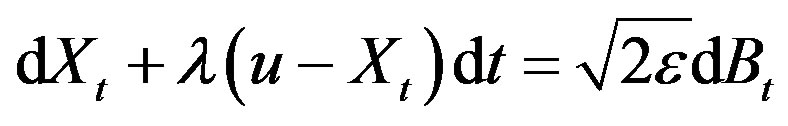 where Bt is the Brownian motion. This type of model has been widely used in Biomathematics (see for example Okubo (1980), Ricciardi (1977) and Taylor (1984)).
where Bt is the Brownian motion. This type of model has been widely used in Biomathematics (see for example Okubo (1980), Ricciardi (1977) and Taylor (1984)).
6Source of data: Alan Heston, Robert Summers and Bettina Aten Penn World Table Version 6.3.
7The process derived from the diffusion model evolves according to an Ornstein-Uhlenbeck, but with a transition, such that the mean tends to u, instead of 0 (Feller 1966). The Ornstein-Uhlenbeck process is the most general normal stationary Markovian process with zero expectations. For t > T, the transition density from (T, s) to (t, y) is normal with expectation e–λ(r – t)s and variance σ2(1 – e–2λ(r – t)). As t →∞, the expectation tends to 0 and the variance to σ2. The analytic solution derived for our diffusion equation is a normal distribution for all t. There is the seλt factor; with a change of variables, it can be shown that the solution is normal with a constant multiplied by it. See [32] for an elaboration.