Feedback Linearization Optimal Control Approach for Bilinear Systems in CSTR Chemical Reactor ()
1. Introduction
Bilinear system is a special nonlinear system, during the processes of the engineering, social economy and ecology, there are so many objects can be described by bilinear systems. Bilinear system is close to linear system in the aspects of form, so some theory of linear systems can be used for bilinear systems. Meanwhile, because of bilinear systems can be approximated as many nonlinear systems, it is more accurate than the traditional linear approximation. Therefore, the study of bilinear systems is becoming particularly important. At present, some research results about the bilinear systems have been obtained. For example, Aganovic proposed a method of global successive approximation about bilinear system [1,2]; DISOPE approximate algorithm based on bilinear model is presented by Li [3]; Tang has studied the optimal control of the discrete bilinear system [4-6]. Hofer and Tibken obtained the optimal solutions in terms of a sequence of the differential Riccati equation [7]. The optimal iterative algorithm based on quadratic performance index about bilinear system is given in the reference [8], etc.
This paper concentrates on the solution of the optimal control problem for bilinear systems with a quadratic criterion based on state feedback. Firstly, the model of the bilinear system is given in this paper and changed to the nonlinear system model; Secondly, a complex nonlinear system model is changed to an easy pseudo linear system model by the differential homeomorphism; Then the optimal control law is designed by solving the Riccati equation; Finally, performance of the obtained optimalcontrol for bilinear systems with a quadratic criterion is verified in the CSTR Chemical reactor example.
The paper is organized as follows. Section 2 states the optimal control problem for bilinear systems. The solution to the optimal control problem and the proof of the obtained results, based on the maximum principle are given in Section 3. Section 4 presents an example illustrating the efficiency of control provided by the obtained optimal regulator for bilinear systems. Simulation graphs demonstrating better performance of the obtained optimal regulator are included.
2. Problem Statement
Consider bilinear systems described by the following difference equations
(1)
where, 
is the state vector; 
is the control vector; 
is the output vector;
, 
, 
are scalar matrixes of appropriate dimensions; 
is the j-th component of state vector;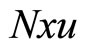 
is the bilinear term; 
is the scalar function of
.
Assumption 1. The relative degree of the output
with respect to the input 
is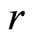
, that is
.
Through exact linearization, we can change the bilinear system (1) to an easy pseudo linear system (2).
(2)
where, 
is the new state vector,
, 
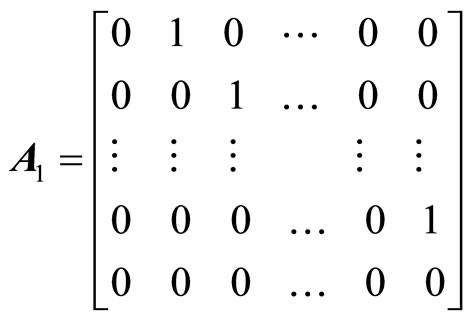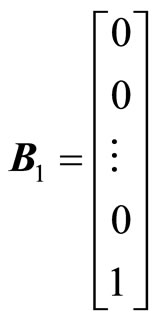
Then we can get the optimal control law base on the pseudo linear system (2).
3. State Feedback Exact Linearization
Transform bilinear system (1) into the general expression of nonlinear system as follow
(3)
where, 
, 
, 
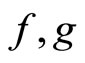are continuously differentiable functions.
Consider the nonlinear systems described by the difference equation, according to Assumption 1, then get
(4)
(5)
Let:
(6)
where 
is the partial differential homeomorphism. We can change system (3) to a new standard form as follow
(7)
In the expression (7), 
and 
are the nonlinear scalar functions. From the first to the 
expressions are linear equations, only an equation which contains the control vector 
is nonlinear. In order to make expression (7) linearizing, let
(8)
Expression (9) can be obtained
(9)
Expression (8) can be written as:
, where,
, 
, 
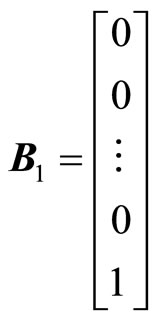
Then the expression of control variable u is obtained.
(10)
4. Optimal Controller Design
Nonlinear system (3) is transformed into equivalent pseudo linear system (2), where v is the control variable of the 
standard form, the linear systems described by the following difference equation
where, z is the new state vector; v is the new control vector; 
is the state coefficient matrix: 
is the control coefficient matrix; system (2) is completely controllable.
Select the quadratic performance index of system (2) as
(11)
where, Q is a positive-semi definite matrix; R is a positive definite matrix.
Lemma 1. The optimal control problem of system (2) with the quadratic performance index (11) is unique existence if the system is completely controllable and observable. It can be expressed as
(12)
where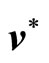 
is the optimal control vector, K is the optimal feedback gain matrix, that is
(13)
P is the unique positive semi-definite solution of the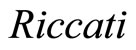 
matrix equation
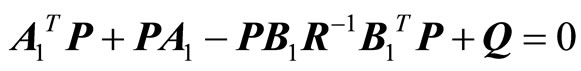(14)
The optimal control law of the system (2) can be found from the following equation
(15)
where, 
can be obtained by Equation (13).
Take Equation (6) into Equation (15), get
(16)
Compare (10) with expression (16), the optimal control law of the nonlinear system (3) is obtained as follow
(17)
Then the optimal control law of the bilinear system (1) is
(18)
The structure diagram is shown as Figure 1.
5. A Simulation Example
In order to illustrate the effectiveness and feasibility of this method, consider Continuous-Stirred Tank Reactor (CSTR) model [9]
, 
,
, 
, 
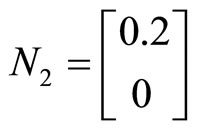
where, the state vector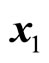 
and 
represent the temperature and density of initial production in the chemical reactor respectively. The control vector u represents the flow rate of cooling in the chemical reactor.
Through computing, we have
(19)
(20)
,
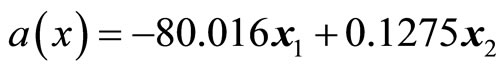
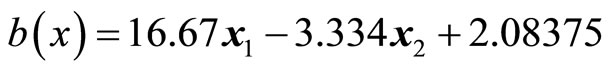
According to the state feedback exact linearization approach of optimal control for bilinear systems, we can get:
(21)
Select
, 
, then
Figure 1. The structure diagram of bilinear system.
Figure 2. The simulation curve of state vector x1(t).
Figure 3. The simulation curve of the state vector x2(t).
Figure 4. The simulation curve of the control vector u(t).
Simulation results are presented in Figures 2-4.
6. Conclusion
We have presented a state feedback exact linearization approach of optimal control for bilinear systems. The precise optimal controller is designed by solving the Riccati equation and introducing state feedback with state prediction. At last, the simulation results in chemical reactor show that the proposed approach is valid and easy to implement, the controller has a good convergence effect.
NOTES