1. Introduction
Many industries evolve over time from an initial monopolistic setting towards more competitive frameworks, with one or more new entrants adding to the incumbent. As long as the number of entrants remains small, however, an environment favorable to collusion is likely to emerge.
Among the set of regulated industries, electricity generation represents a good benchmark for the theoretical analysis developed in the present paper. First, in electricity generation, firms engage in a dynamic game, characterized by frequent interactions, information transparency, as well as by high time-sensitivity of demand, so that for most of the time a large portion of the installed industry capacity remains idle. All the above characteristics are recognized in the literature as facilitating factors for collusion. Second, electricity is an industry typically dominated by a large incumbent, who faces the (potential) competition by new entrants.1 Turning now towards unregulated industries, the airplane industry may fit the framework developed in this paper nicely. The increase in demand, coupled with the development of technologies reducing the optimal size of planes, may generate room for more than one firm in many routes. At the same time, the frequency of interactions lets us suppose that, once capacity is installed, the firms will engage in a repeated game, where collusion may emerge.
The future entry prospects may not be reasonably anticipated at the time of the incumbent’s investment. For example, in electricity, the incumbent firms in various countries made their investment decisions in a regulated environment, while they were often enjoying legal monopolies in their home market. The former integrated monopolies had neither the incentives nor the mandate to calibrate their capacity in view of future entry. In the airplane industry, uncertainty over the technological evolution may suggest the monopolists to calibrate their capacities on the current demand and cost structures, while revising their choices in the future if needed. Following this motivation, in this paper we regard the incumbent’s decision as exogenous, and we analyze a two stage game. In the first (entry) stage, a potential new entrant decides whether or not to enter the market. In the (second) productive stage, the firms engage in a repeated game and collude on prices whenever it is rational for them to do so. The remainder of the paper is organized as follows. Section 2 provides a literature review. Section 3 illustrates the model. Section 4 summarizes the main results, and Section 5 concludes.
2. Literature Review
The model developed in Section 3 has several points of contact with the papers dealing with multiple stage games, and analyzing how firms’ capacities affect the outcome, under a variety of game formats, and different hypotheses on both the forms of competition at various stages, and the timing of entry.
The first of these papers is by Kreps and Scheinkman (KS) [2], who examine a simultaneous capacity game, followed by a price competition stage. They find that this game structure yields the Cournot outcome, highlighting also that a limited capacity has the effect of relaxing price competition. Brock and Scheinkman (BS) [3] consider capacity as exogenous, and analyze a repeated price game, where firms collude whenever it is rational for them do so. They illustrate how aggregate capacity shapes the threat after a deviation, by explicitly analyzing the tradeoffs between the two countervailing effects of a capacity increase. On the one hand, as long as the individual firms’ initial capacity stock is not sufficient to cover the entire market demand, a larger capacity (weakly) increases the one-shot deviation profit, by allowing the firm to increase the output produced right after the deviation occurs. This contributes to making collusion more difficult to sustain. On the other hand, until aggregate capacity is sufficiently low that all of the firms are needed to contribute to production to reach the competitive outcome (i.e., the capacity of all the firms except for the largest one is not sufficient to cover the market demand at the competitive price), profits involved in the static Bertrand equilibrium are decreasing in aggregate capacity. Therefore, if each firm proportionally increases capacity, the individual continuation profit is reduced, thereby increasing the collusive potential. The intensity of each of the two effects depends on the initial capacity stock. When it is low (high), the second (first) effect is prevailing, and adding capacity facilitates (hinders) collusion. Therefore, an increase in aggregate capacity has a non-monotonic effect on the sustainability of the cartel. Davidson and Deneckere (DD) [4] analyze a framework similar to BS. However, it substantially differs in that capacity is endogenously chosen in a noncooperative fashion; a repeated game, analogous to BS, follows. DD find that carrying (idle) excess capacity favors the emergence of collusive behavior. They also find that capacity levels and collusion both increase if the discount factor rises or the cost of capacity declines. With a low discount factor, or a high capacity cost, it becomes too costly to carry enough capacity to support the monopoly equilibrium. Benoit and Krishna [5] allow for the option of adjusting capacity every period, and find a set of equilibria sharing the property that in equilibrium firms carry excess capacity.
The stream of literature on sequential entry has analyzed both static and dynamic competition (in prices or quantities). The standard results for static competition, in both prices and quantities, after sequential entry (see Spence [6] and Dixit [7]) indicate that entry may be deterred by installing a sufficiently high capacity, as this represents a commitment towards an aggressive behavior on the incumbent’s part, if entry had to take place. When the post-entry structure is modeled as a dynamic gamethe reasoning changes dramatically. As Benoit and Krishna (BK) [8] point out “commitments that make predatory behavior in the post-entry game credible also increase the prospects for collusion. This is because in a dynamic setting, a greater degree of collusion may be supported by the increased severity of available threats. The entrant may view the incumbent’s choice as a commitment to collude”. While in a static setting high capacity provides the incumbent with a commitment towards aggressive behavior if entry occurred, in a dynamic setting this same strategy may be interpreted as a commitment to collude (as it reduces the continuation profit after deviation). Table 1 provides a useful categorization of the above mentioned papers.
In our paper, we consider the incumbent’s capacity as exogenous, and we model the entrant’s response in view of a post-entry dynamic price game. We examine the role of the discount factor in determining the outcome of the new entrant’s capacity choice followed by a dynamic price game. We find that the entrant’s capacity choices are such that the non-cooperative behavior prevails for sufficiently high discount factor levels, while the static one-shot equilibrium prevails even in the dynamic game for a low level of the discount factor. When the discount factor is high, the entrant enjoys a more significant benefit from additional capacity, while the capacity cost remains constant. As the discount factor increases, excess capacity increases as well, thereby creating potential inefficiencies. The entrant expands its capacity beyond the level it will use not only for the standard reason of being able to sustain the collusive arrangement, but also to increase its production share within the cartel. This is due to the adopted sharing rule.
3. A Model of Entry and Collusion
We consider an incumbent I who installs monopoly capacity. After some (possibly exogenous) regulatory or technological changes, entry becomes a feasible option, so that I faces the threat of competition by a potential new entrant E. E decides whether or not to enter. If it enters, it will tacitly collude with the incumbent when it is rational for him to do so. The stages of the game are the following: 0) I is exogenously assigned a capacity level, assumed to be at the monopoly level; 1) E decides whether to enter or not, and, if entry occurs, chooses the capacity level; 2) an infinitely repeated production game is played.
We aim at investigating how the collusive potential, after the incumbent’s monopoly choice, affects the entrant’s decisions and the outcome of the game. We make the following assumptions: 1) Firms face a unit linear demand: p = 1 – Q; 2) There is a fixed/sunk cost of entry F, which will remain implicit in the rest of the model; 3)
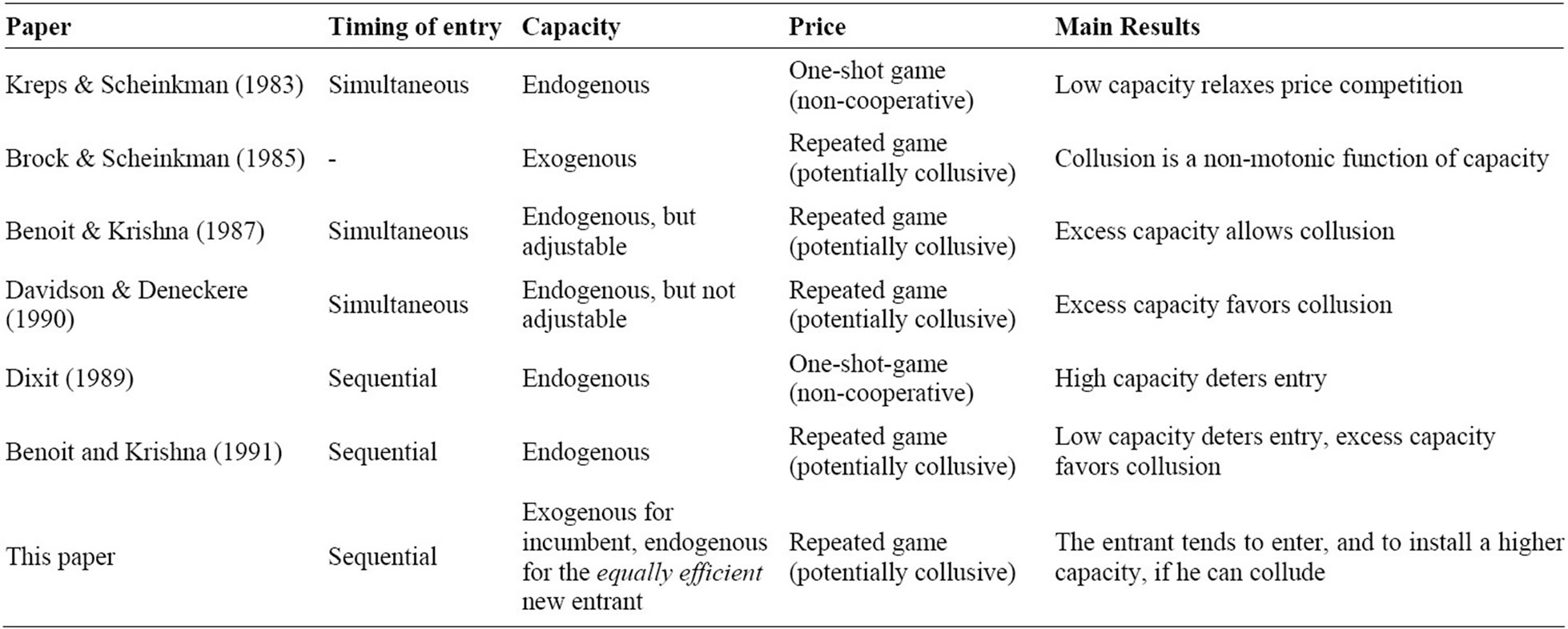
Table 1. Capacity, entry and collusion.
Each unit of installed capacity has a cost of r = 1/2; 4) There are zero marginal production costs; 5) The following sharing rule is in place  and
and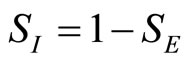 , where S is the market share; 6)
, where S is the market share; 6) .
.
Assumptions 3) and 4) prescribe a positive cost of capacity and symmetric marginal costs. Assumption v) represents a quite common sharing rule (see Davidson and Deneckere [4]), which is consistent with most empirical observations. Assumption 6) reflects a feature of recently privatized and liberalized industries, where a large formerly State-owned monopolist faces the prospect of new entrants, which normally start operation on a smaller scale.
3.1. Monopoly Choice by I
We first derive the investment and price choices for a monopolist wishing to maximize profit neglecting the threat of potential entry. In such case,
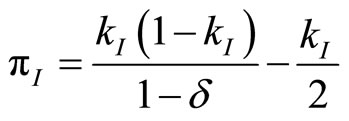 . Maximization with respect to
. Maximization with respect to  yields
yields .
.
As the discount factor increases, the cost of capital remains constant, while the relative value of future revenue streams grows. As a result the optimal capacity investments increases with the discount factor. The single period price and discounted profits are respectively equal to:
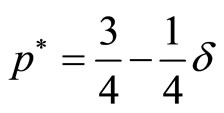 and
and .
.
3.2. The New Entrant’s Choice
In choosing its scale of operation, the new entrant considers four effects of a marginal increase in capacity.
First, as long as capacity lies above the static monopoly output, the static game profit is decreasing, due to the retaliatory reaction after a deviation from the collusive arrangement takes place. This effect encourages collusion, by making a deviation less appealing.
Second, there is an increase in the chiseling profit, that reduces the cartel stability and (weakly) decreases E’s profits.
Third, if a monopolistic cartel is still prevailing, the entrant’s production share in the arrangement, as well as E’s profits, are increased.
Fourth, the increase in capacity trivially increases the capacity costs, and directly reduces E’s profits. The interplay among these four effects determines E’s choices. In analyzing the entrant’s choice, we are restricting ourselves to our assumption 6) 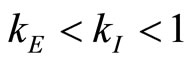
Following Davidson and Deneckere [4], we split the analysis into different sub-cases:
1) 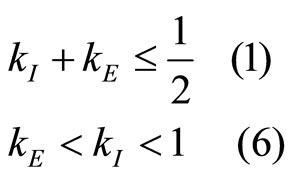
2) 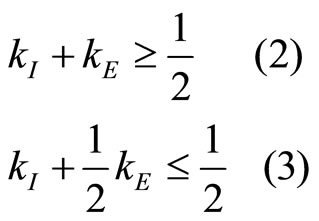
3) 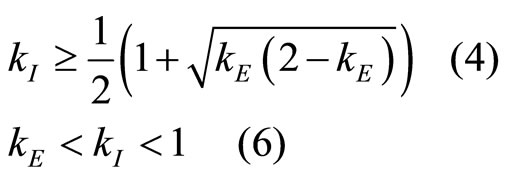
The logic for the need to separate the analysis into multiple groups is the following. The dynamic game profit, along with the output sustainable in a collusive agreement, depends on the Bertrand profit, which constitutes the continuation profit accruing to a firm that decides to deviate from the arrangement, within a Nash reversion setting. The Bertrand profit function is a step function, with multiple functional forms for different ranges of values for 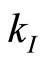 and
and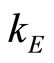 . Hence the need to analyze each case separately.
. Hence the need to analyze each case separately.
3.2.1. Case 1)
In this case, the aggregate capacity is below the monopoly output in the stage game (which is equal to 1/2). Using the fact that , we rewrite (1) as
, we rewrite (1) as 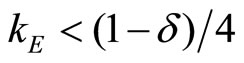 and (vi) as
and (vi) as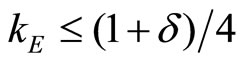 : both firm’s capacities are entirely absorbed by the market, and the equilibrium price tops the monopoly price. Clearly, (1) is more stringent than 6), and therefore it’s the relevant one. Hence, the price equals:
: both firm’s capacities are entirely absorbed by the market, and the equilibrium price tops the monopoly price. Clearly, (1) is more stringent than 6), and therefore it’s the relevant one. Hence, the price equals: . The objective function for E is then:
. The objective function for E is then:

At the unconstrained optimum, we have .
.
We need to verify that constraint (1) holds:
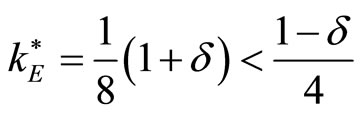 , which holds only for
, which holds only for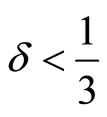 . It follows that the optimal output and the resulting profit in case 1) are respectively:
. It follows that the optimal output and the resulting profit in case 1) are respectively:
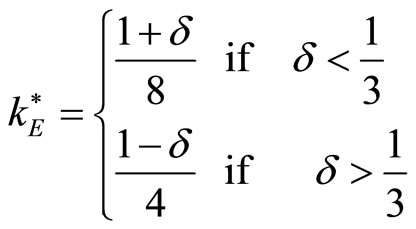
and
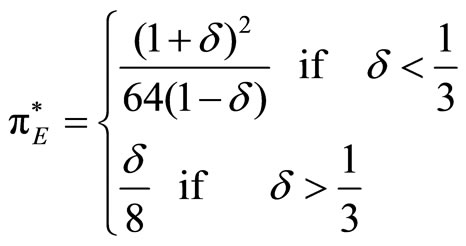
3.2.2. Case 2)
In this case, the aggregate industry capacity kI + kE exceeds the monopoly output in the stage game (equal to 1/2), but only by a limited amount. Using the fact that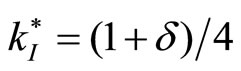 , we rewrite (2) as
, we rewrite (2) as  and (3) as
and (3) as . Therefore, the Bertrand equilibrium involves no capacity restriction, and every firm entirely utilizes its capacity. Since aggregate industry capacity is only slightly higher than 1/2, the profit in the static game is only modestly lower than the optimal (i.e., monopoly) profit. The significance of the deviation profit makes collusive agreements very unstable, and ultimately hinders collusion. Even in this case the outcome is a repetition, at each stage, of the static game outcome:
. Therefore, the Bertrand equilibrium involves no capacity restriction, and every firm entirely utilizes its capacity. Since aggregate industry capacity is only slightly higher than 1/2, the profit in the static game is only modestly lower than the optimal (i.e., monopoly) profit. The significance of the deviation profit makes collusive agreements very unstable, and ultimately hinders collusion. Even in this case the outcome is a repetition, at each stage, of the static game outcome:  . By verifying the compatibility with constraints (2), (3), and (6), it follows that the optimal output and the corresponding profits in case 2) are the following:
. By verifying the compatibility with constraints (2), (3), and (6), it follows that the optimal output and the corresponding profits in case 2) are the following:
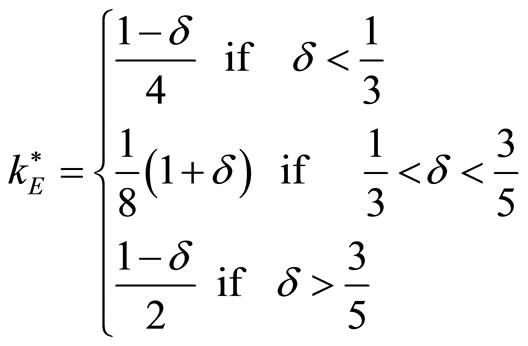
and
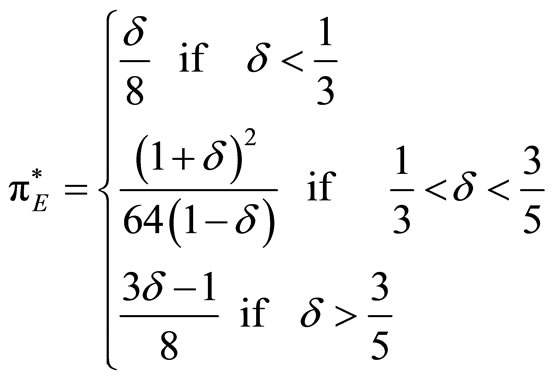
3.2.3. Case 3)
Case 3) is the only one where we observe equilibrium excess capacity.
 (4)
(4)
For such a high (relative to cases 1) and 2)) aggregate capacity, the Bertrand equilibrium involves a capacity restriction, as each firm’s optimal response to the rival’s prescribes a limited production. This implies that the Bertrand equilibria of the one-shot game involve mixed strategies. Aggregate capacity under this circumstance is relatively high, so that the threat to resort to a competetive outcome is sufficiently severe to constitute a deterrent from deviation, and, as a consequence, to allow for a monopolistic outcome. Observe that the prevalence of the collusive outcome entails the enactment of the sharing rule.
Rewriting (4) and replacing for the incumbent’s capacity level, we have: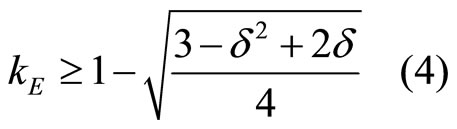 . In this case, the size of capacity is relevant enough to generate a relatively low Bertrand profit. The low continuation profit reduces the temptations to deviate, thereby increasing the prospects of an effective cartel enforcement. Clearly, however, the chances to support a collusive equilibrium depend on the discount factor, which has to be sufficiently high. The standard collusive individual rationality constraints, one for E and one for I, are:
. In this case, the size of capacity is relevant enough to generate a relatively low Bertrand profit. The low continuation profit reduces the temptations to deviate, thereby increasing the prospects of an effective cartel enforcement. Clearly, however, the chances to support a collusive equilibrium depend on the discount factor, which has to be sufficiently high. The standard collusive individual rationality constraints, one for E and one for I, are:
 (5a)
(5a)
and
 (5b)
(5b)
Aggregating 5(a) and 5(b), we derive condition (6):
 (6)
(6)
We do not solve analytically for Equation (6). However, we compute the maximal value of  compatible with a variety of given levels of discount factors. In choosing the optimal
compatible with a variety of given levels of discount factors. In choosing the optimal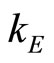 , the entrant solves the following maximization problem:
, the entrant solves the following maximization problem:
 (7)
(7)
under the constraint (6)2 and under the fact that 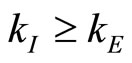
Equation (7) specifies that the collusive profit is given by the difference between the collusive revenue
 and the cost
and the cost . The collusive revenue is composed of the share of the collusive output (1/2) computed according to the previously described sharing rule multiplied by the collusive price 1/2.
. The collusive revenue is composed of the share of the collusive output (1/2) computed according to the previously described sharing rule multiplied by the collusive price 1/2.
Given the first order conditions, Equation (7) yields
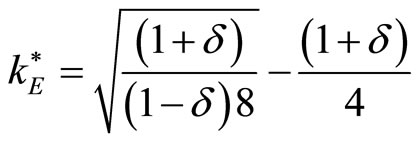
(7) is compatible with  only for
only for .
.
4. Results
With the help of Tables 2 and 3 and Figures 1 and 2, we summarize the results for the different discount factors.
For 0 < δ < 1/3 the sum of the incumbent’s capacity and of the entrant’s optimal capacity choice yields an output below the stage game monopoly quantity. Carrying enough capacity to sustain a monopolistic outcome in the stage game would be too costly for the entrant. Therefore case 1) prevails.
For 1/3 < δ <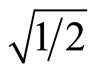 , we jump to case 3), where the collusive monopolistic outcome prevails, and an excess capacity which increases steadily with δ is prevailing.
, we jump to case 3), where the collusive monopolistic outcome prevails, and an excess capacity which increases steadily with δ is prevailing.
For δ > , the constraint 6) is binding, and kE = kI. Even in this case, collusion prevails.
, the constraint 6) is binding, and kE = kI. Even in this case, collusion prevails.
While Table 2 reports the optimal values of kE, kI,, πE, πI, for cases 1), 2) and 3), and cases with thick borders detect the preferred entrant’s choice for different values of δ, Table 3 exemplifies the outcomes for some point values of the discount factor. In the same vein, Figure 1 compares case 1), where the aggregate capacity is below 1/2, and case 2), which is associated with a higher aggregate capacity. As it is shown, the entrant’s profits in case b) bypass profits in case 1) for δ > 1/3.
Finally, Figure 2 compares the “competitive” case, by taking, for each δ, the highest profit value between cases 1) and 2), versus the collusive one. For large enough values of the discount factor, when the capacity cost is

Figure 1. Cases 1) and 2): Entrants’ profits for different discount factors.
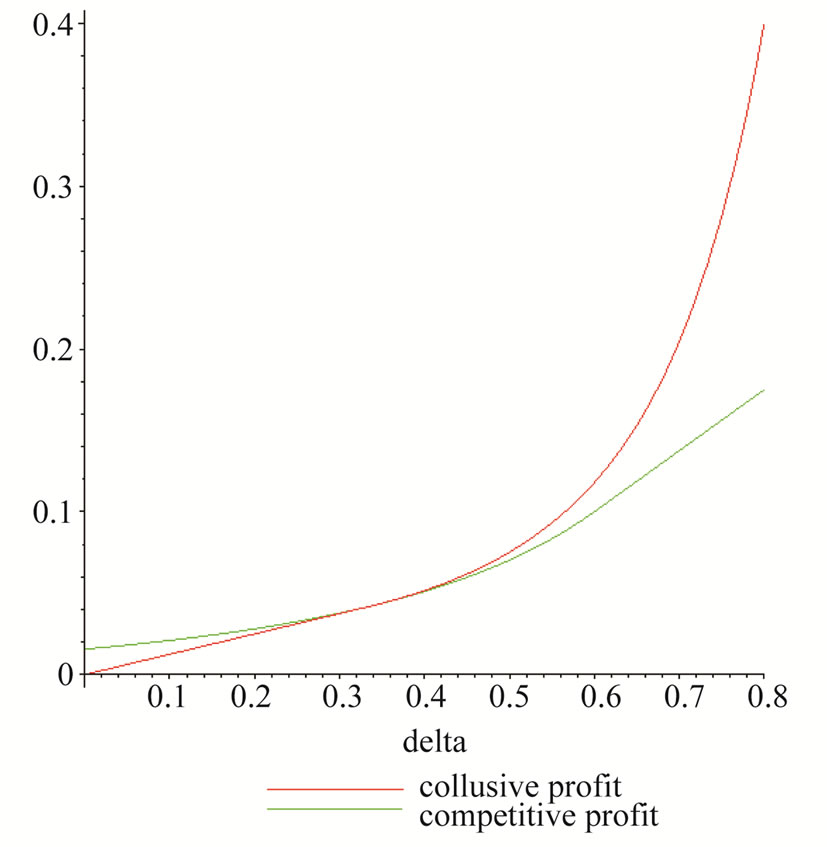
Figure 2. Competition versus collusion (case 3): Entrants’ profits for different discount factors.
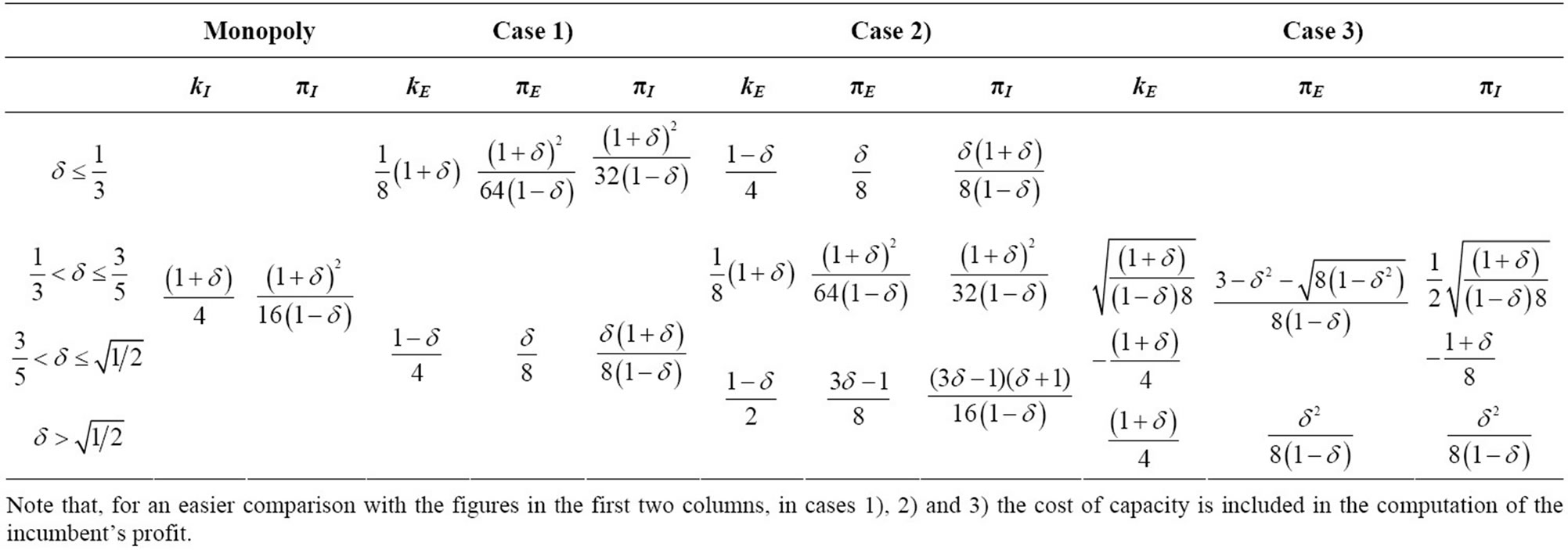
Table 2. The outcome of the game in the three cases.

Table 3. The equilibrium outcome for the various discount factors.
relatively low with respect to the revenue stream, case 3) prevails.
5. Conclusions
Our model shows that, in a dynamic context, higher capacity increases the severity of punishment after a deviation, thereby favoring the emergence of cartels. The cartel is effective under a high value of the discount factor, where carrying idle capacity would be too costly. When the discount factor is high, the new entrant increases capacity in order to be able to sustain a collusive arrangement. Our results confirm Davidson and Deneckere’s [4] findings, even in the context of a sequential game with exogenous capacity by the incumbent.
The cartel in this case could hurt welfare, because of the cost inefficiency due to high and idle capacity. Indeed, an interesting result is that both blockaded entry (which occurs when sunk costs of entry, F, are sufficiently high), and entry with small capacity, occur when the Antitrust Authority enforces a competitive behavior, and in both cases the position of the incumbent is improved too. As a result of this, we conjecture that a competitive arrangement could be both welfare enhancing, as well as profit-maximizing for the incumbent. Therefore, a strict Antitrust enforcement, along with pro-competitive arrangements in which the incumbent is forced to transfer part of its capacity to the new entrant, could be welfare-enhancing.
This paper could be fruitfully extended in two directions. First, one might analyze a sequential capacity choice game, followed by, rather than price competition, dynamic Cournot competition. It would be interesting to check under what conditions the first mover advantage would persist in this game.
A second interesting addition might consist in considering alternative initial capacity levels for the incumbent, so as, for example, to be able to deal with cases in which regulation imposes higher production than the one considered in Section 3.1. Our preliminary intuition is that, as I’s capacity gets larger, a collusive behavior is more likely to occur.
NOTES
2Observe that, on the other hand, if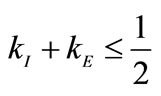 ,
,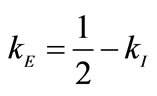 . Notice that, for
. Notice that, for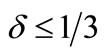 , the collusive monopolistic outcome would imply an (incompatible) aggregate capacity below 1/2.
, the collusive monopolistic outcome would imply an (incompatible) aggregate capacity below 1/2.