Solitary Wave Solution of the Two-Dimensional Regularized Long-Wave and Davey-Stewartson Equations in Fluids and Plasmas ()
1. Introduction
In the recent years, seeking exact solutions of nonlinear partial differential equations (NLPDEs) is of great significance, since the nonlinear complex physical phenomena related to the NLPDEs are involved in many fields from physics (plasma physics, optical fibers, solid state physics, nonlinear optics and so on), fluid mechanics, biology, chemistry kinetics, geochemistry and engineering. As mathematical models of the phenomena, the investigation of exact solutions of NLPDEs will help one to understand the mechanism that governs these physical models or to better provide knowledge of the physical problem and possible applications. To this aim, a vast variety of powerful and direct methods for finding the exact significant solutions of the NLPDEs through it is rather difficult have been derived. Some of the most important methods are Hirota’s dependent variable transformation [1], the Bäcklund transformations (BTs) [2], the inverse scattering transformation [3], Painlevé expansions [4], Jacobi elliptic function expansion method [5-7], the homogenous balance method [8], the linearized transformation method [9-11], the F-expansion method [12,13], Fan-sub-equation method, extended and modified extended Fan-sub equation method [14-18], the tanh-function method and extended tanh-function method [19-21], the tanh-sech method [22], the sine-cosine method [23,24], variational iteration method [25], homotopy perturbation method [26], the  -expansion method [27-29] and several ansatz methods [30-34].
-expansion method [27-29] and several ansatz methods [30-34].
The Frobenius integrable decompositions (FIDs) and rational function transformations (RFTs) are used to construct exact solutions to NLPDEs with BTs and auto BTs [35-40]. Recently, Ma et al. [37] presented Frobenius integrable decompositions (FIDs) for two classes of nonlinear evolution equations (NEEs) with logarithmic derivative BTs in soliton theory. The discussed NEEs are transformed into systems of Frobenius integrable ODEs with cubic nonlinearity. You et al. [41] obtained two classes of PDEs with variable coefficients possessing FIDs, including the KdV and the potential KdV equation, the Boussinesq equation, and the generalized BBM equation. The RFTs method is very suitable for an easier and more effective handling of the solution process of nonlinear equations, unifying the existing solution methods mentioned above. Its key point is to find rational solutions to variable-coefficient ODEs transformed from given NLPDEs, together with an auto-BT.
The main aim of this paper is to find exact solitary solutions of (2+1) dimensional regularized long wave (2DRLW) and (2+1) Davey-Stewartson (DS) equations. The paper is organized as follows: This introduction is presented in Section 1. In Section 2 we give a description of the extended mapping method and we apply this method to the (2+1) regularized long wave equation and the Davey-Stewartson equation. In Section 3, some conclusions are given.
2. The Extended Mapping Method
We are given a NLPDE for  in the form
in the form
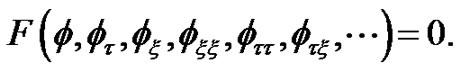 (1)
(1)
Introducing the similarity variable , then the function
, then the function  satisfies the following ordinary differential equation (ODE)
satisfies the following ordinary differential equation (ODE)
 (2)
(2)
By virtue of the extended mapping method we assume that the solution of Equation (2) in the form
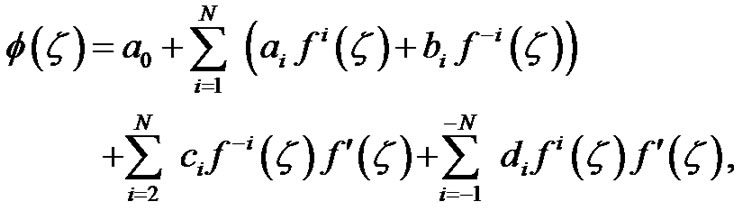 (3)
(3)
where  in Equation (3) is a positive integer that can be determined by balancing the nonlinear term(s) with the highest derivative term in Equation (2) and a,
in Equation (3) is a positive integer that can be determined by balancing the nonlinear term(s) with the highest derivative term in Equation (2) and a,  ,
,  ,
,  and
and  are constants to be determined. The function
are constants to be determined. The function  satisfies the nonlinear ODE
satisfies the nonlinear ODE
 (4)
(4)
where  and
and  are constants. Substituting Equation (3) with Equation (4) into the ODE Equation (2) and setting the coefficients of the different powers of
are constants. Substituting Equation (3) with Equation (4) into the ODE Equation (2) and setting the coefficients of the different powers of  to zero yields a set of algebraic equations for
to zero yields a set of algebraic equations for ,
,  ,
,  ,
,  ,
,  and
and . Solving the algebraic equations by use of Maple or Mathematica, we have
. Solving the algebraic equations by use of Maple or Mathematica, we have ,
,  ,
,  ,
,  ,
,  and
and  expressed by
expressed by . Substituting the obtained coefficients into Equation (3), then concentration formulas of travelling wave solutions of the NLPDE Equation (1) can be obtained. Selecting the values of
. Substituting the obtained coefficients into Equation (3), then concentration formulas of travelling wave solutions of the NLPDE Equation (1) can be obtained. Selecting the values of  and the corresponding JEFs
and the corresponding JEFs  from the table in Appendix and substituting them into the concentration formulas of solutions to obtain the explicit and exact JEF solutions of Equation (1). Various solutions of Equation (4) were constructed using JEFs, and these results were exploited in the design of a procedure for generating solutions of NLPDEs. The JEFs
from the table in Appendix and substituting them into the concentration formulas of solutions to obtain the explicit and exact JEF solutions of Equation (1). Various solutions of Equation (4) were constructed using JEFs, and these results were exploited in the design of a procedure for generating solutions of NLPDEs. The JEFs 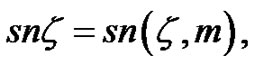
 and
and 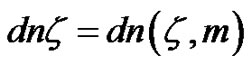 where
where
 is the modulus of the elliptic function, are double periodic and posses the following properties
is the modulus of the elliptic function, are double periodic and posses the following properties


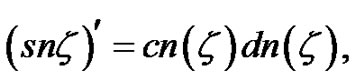


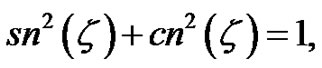
In addition when , the functions
, the functions 
 and
and  degenerate as
degenerate as 
 and
and , respectively, while when
, respectively, while when ,
, 
 and
and  degenerate as
degenerate as 
 and 1, respectively. So, we can obtain hyperbolic function solutions and trigonometric function solutions in the limit cases when
and 1, respectively. So, we can obtain hyperbolic function solutions and trigonometric function solutions in the limit cases when  and
and . Some more properties of JEFs can be found in [33].
. Some more properties of JEFs can be found in [33].
2.1. (2+1) Regularized Long Wave Equation
Let us first consider the regularized long wave equation:
 (5)
(5)
have been reported in [42,43] where the coefficients β1, 
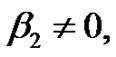 γ2,
γ2,  and
and  are all constants. Equation (5) is related to the drift waves in plasma and the Rossby waves in rotating fluids [44]. To look for travelling wave solution of Equation (2.5), we make transformation
are all constants. Equation (5) is related to the drift waves in plasma and the Rossby waves in rotating fluids [44]. To look for travelling wave solution of Equation (2.5), we make transformation 
 and change Equation (5) into the form
and change Equation (5) into the form
 (6)
(6)
where 
 and
and
 Integrating once with respect to ξ and setting the integration constant equal to zero, one has
Integrating once with respect to ξ and setting the integration constant equal to zero, one has
 (7)
(7)
Balancing  with
with 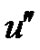 gives the leading order
gives the leading order . So take the anastz
. So take the anastz
 (8)
(8)
where ,
,  ,
,  ,
,  ,
,  ,
, 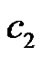 ,
,  ,
,  and
and  are constants and need to be determined,
are constants and need to be determined,  is a solution of Equation (4). Substituting Equation (4) and Equation (8) into Equation (7) and setting the coefficients of
is a solution of Equation (4). Substituting Equation (4) and Equation (8) into Equation (7) and setting the coefficients of , to zero, we get a system of nonlinear equations for
, to zero, we get a system of nonlinear equations for ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and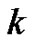 . Solving this system by use of Mathematica, we obtain:
. Solving this system by use of Mathematica, we obtain:
Case

 (9)
(9)
Case 1

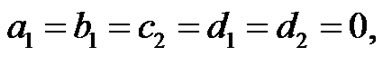


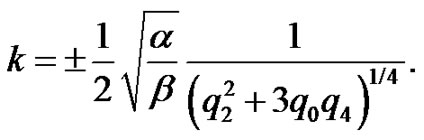 (10)
(10)
Case 2

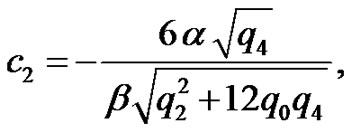

 (11)
(11)
Case 3

 ,
,
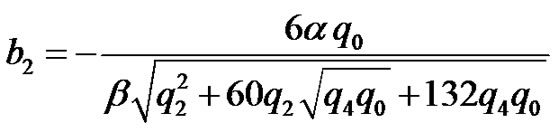 ,
,
 ,
,
 ,
,
 (12)
(12)
If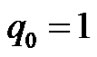 ,
,  ,
, 
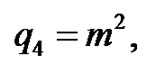 this yields the exact solutions of Equation (7) as follows:
this yields the exact solutions of Equation (7) as follows:
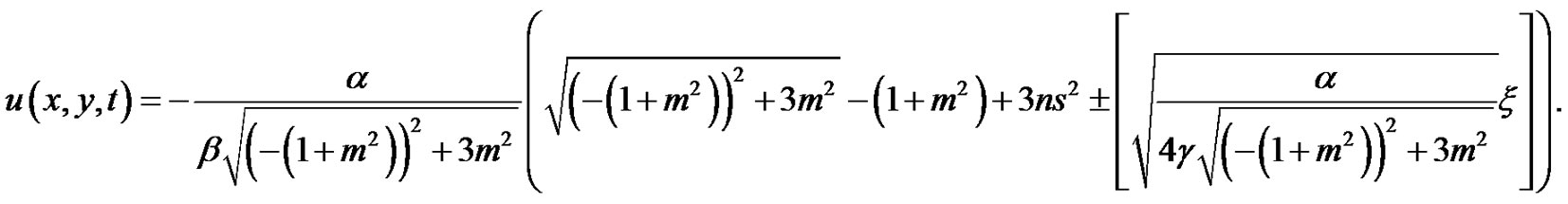 (13)
(13)
when , the solitary wave solutions of Equation (5) are obtained as follows:
, the solitary wave solutions of Equation (5) are obtained as follows:
 (14)
(14)
We have represented this solution for a set of parameter values in Figure 1(a).
When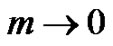 , the triangular periodic solutions of Equation (5) are obtained as follows:
, the triangular periodic solutions of Equation (5) are obtained as follows:
 (15)
(15)
We have represented this solution for a set of parameter values in Figure 1(b).
If ,
,  ,
, 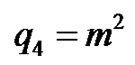 ,
,  and when
and when , this yields the solitary solutions of Equation (5) as follows:
, this yields the solitary solutions of Equation (5) as follows:
 (16)
(16)
We have represented this solution for a set of parameter values in Figure 1(c).
If ,
,  ,
,  ,
, 
and when , this yields the solitary solutions of Equation (5) as follows:
, this yields the solitary solutions of Equation (5) as follows:
 (17)
(17)
We have represented this solution for a set of parameter values in Figure 1(d).
If ,
,  ,
,  ,
,  and when
and when , this yields the solitary solutions of Equation (5) as follows:
, this yields the solitary solutions of Equation (5) as follows:
 (18)
(18)
We have represented this solution for a set of parameter values in Figure 1(e).
2.2. The Davey Stewartson Equation
The dimensionless form of the DSE in (2+1) dimensions, with power law nonlinearity [45]. The DS model is exactly integrable in shallow water and almost integrable in deep water. Furthermore, the model has easily identifiable coherent structures and waves, including solitons, unstable rogue-wave type modes, Stokes waves and the velocity field contains vortices,
 (19a)
(19a)
 (19b)
(19b)
Here, in Equations (19a) and (19b),  and
and  are the dependent variables while
are the dependent variables while  and
and  are the independent variables. The first two of the independent variables are the spatial variables while t represents time. In Equations (19a) and (19b),
are the independent variables. The first two of the independent variables are the spatial variables while t represents time. In Equations (19a) and (19b),  is a complex valued function while
is a complex valued function while  is a real valued function. Also,
is a real valued function. Also,  are all constant coefficients. For solving the Equations (19a) and (19b) with the extended mapping method, using the wave variables
are all constant coefficients. For solving the Equations (19a) and (19b) with the extended mapping method, using the wave variables
 , (20a)
, (20a)
 , (20b)
, (20b)
where both  and
and  are real functions,
are real functions,  ,
,  ,
,  ,
,  ,
,  and
and  are constants and
are constants and 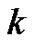 is a constant determine later. Substituting Equations (20a) and (20b) into Equations (19a) and (19b), we have the following ODE for
is a constant determine later. Substituting Equations (20a) and (20b) into Equations (19a) and (19b), we have the following ODE for  and
and 
 (21a)
(21a)
 (21b)
(21b)
If we set
 (22)
(22)
then Equation (21a) reduce to
 . (23)
. (23)
Integrating Equation (21b) twice, and we take the constant of integration equal zero, we have
 (24)
(24)
Substituting Equation (24) into Equation (23) yields
 (25)
(25)
 , (26)
, (26)
where
 ,
, 
and
 .
.
Balancing 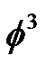 with
with  gives the leading order
gives the leading order . So take the anastz
. So take the anastz
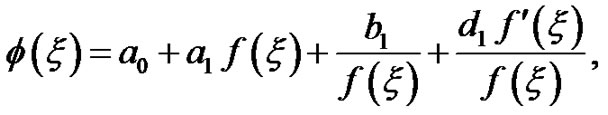 (27)
(27)
where ,
,  ,
,  ,
,  and
and  are constants and need to be determined,
are constants and need to be determined, 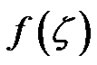 is a solution of Equation (4). Substituting Equations (4) and (27) into Equation (26) and setting the coefficients of
is a solution of Equation (4). Substituting Equations (4) and (27) into Equation (26) and setting the coefficients of , to zero, we get a system of nonlinear equations for
, to zero, we get a system of nonlinear equations for ,
,  ,
, 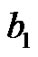 ,
,  and
and . Solving this system by use of Maple, we obtain:
. Solving this system by use of Maple, we obtain:
Case
 (28)
(28)
Case 1
 (29)
(29)
Case 2
 (30)
(30)
Case 3
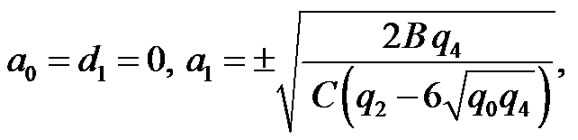
 (31)
(31)
Case 4
 (32)
(32)
If ,
,  ,
,  ,
,  , we can obtain one Jacobian elliptic function solution of Equation (26) as follows:
, we can obtain one Jacobian elliptic function solution of Equation (26) as follows:
 (33)
(33)
when , the solitary solutions of Equations (25) and (24) are obtained as follows:
, the solitary solutions of Equations (25) and (24) are obtained as follows:
 (34)
(34)
We have represented this solution for a set of parameter values in Figure 2(a).
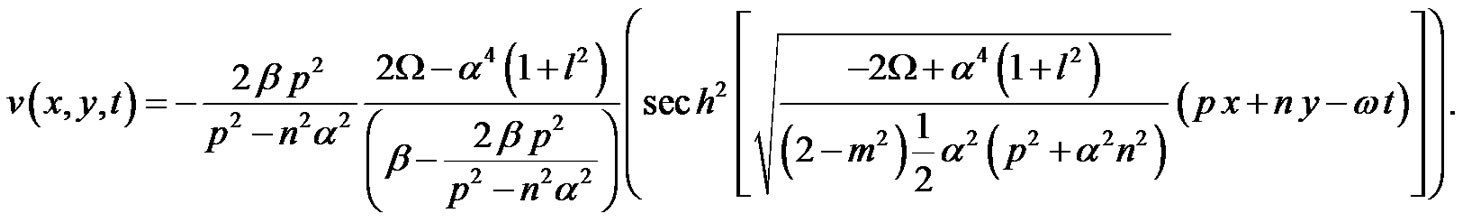 (35)
(35)
If ,
, 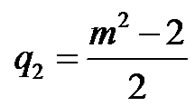 ,
,  ,
,  this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
 (36)
(36)
We have represented this solution for a set of parameter values in Figure 2(b).
 . (37)
. (37)
If ,
, 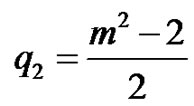 ,
,  ,
,
 , this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
, this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
 (38)
(38)
We have represented this solution for a set of parameter values in Figure 2(c).
 (39)
(39)
If ,
,  ,
, 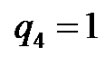 ,
,  , this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
, this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
 (40)
(40)
We have represented this solution for a set of parameter values in Figure 2(d).
 (41)
(41)
If ,
,  ,
,  ,
,  , this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
, this yields the solitary wave solutions of Equations (25) and (24) are obtained as follows:
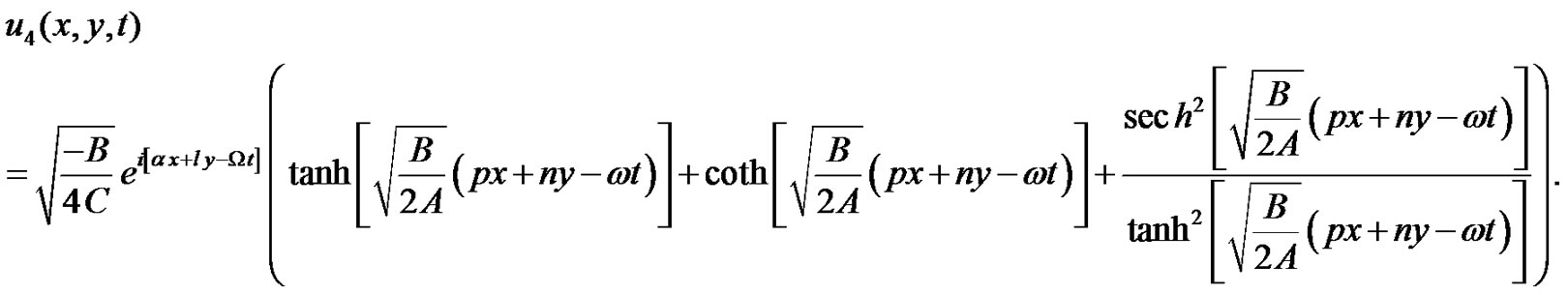 (42)
(42)
We have represented this solution for a set of parameter values in Figure 2(e).
 (43)
(43)
3. Conclusion
In the current article, the solitary wave solutions of the two dimensional regularized long-wave equation in plasma and rotating flows simulated by using extended mapping method, and we hope these solitary waves are helpful to understand the nonlinear phenomena described by the resonant Davey-Stewartson equation in the fields like capillarity fluids. We have presented the extended mapping method to construct more general exact solutions of NLPDEs with the help Maple and Mathematica. This method provides a powerful mathematical tool to obtain more general exact solutions of a great many NLPDEs in mathematical physics. Applying this method to the 2DRLW and DS equations and we have successfully obtained many new exact travelling wave solutions.
Through our solutions for some partial differential equations non-linear, we found lack of interest in these two methods by the specialists with the knowledge that they give an solutions more realistic than many ways, espe-
 (a)
(a) (b)
(b) (c)
(c)  (d)
(d) (e)
(e)
Figure 2. The solitary wave solution represented by Equations (34), (36), (38), (40) and (42) for various values α = 1, β = 2, l = 0.9, n = 2, Ω = 3; p = 0.5, t = 7, for Figures 2(a), 2(b), 2(c), 2(d), 2(e) respectively.
cially as they deal with the equations of non-linear coefficients fixed and transactions variable, which explain the phenomena, physical and in the various sciences. In my view this lack of interest due to the ease of the abovementioned methods.
4. Acknowledgements
It is a pleasure to thank the referee for critical comments on this work.
Appendix
Relation between values of ( ,
, ) and corresponding
) and corresponding 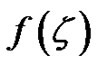 in ODE
in ODE 